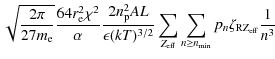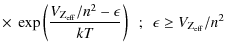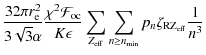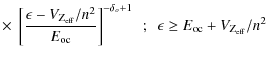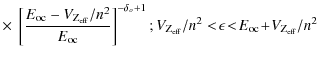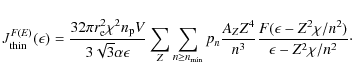| Issue |
A&A
Volume 515, June 2010
|
|
|---|---|---|
| Article Number | C1 | |
| Number of page(s) | 3 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361:20078103e | |
| Published online | 10 June 2010 | |
Non-thermal recombination - a neglected source of
flare hard X-rays and fast electron diagnostics
(Corrigendum)
J. C. Brown1 - P. C. V. Mallik1 - N. R. Badnell2
1 - Department of Physics and Astronomy, University of
Glasgow, Glasgow G12 8QQ, UK
2 - Department of Physics, University
of Strathclyde, Glasgow G4 0NG, UK
A&A, 481, 507-518 (2008), DOI: 10.1051/0004-6361:20078103
Abstract
Brown and Mallik (BM) recently claimed that non-thermal
recombination (NTR) can be a dominant source of flare hard X-rays
(HXRs) from hot coronal and chromospheric sources. However, major
discrepancies between the thermal continua predicted by BM and by the
Chianti database as well as RHESSI flare data, led us to discover
substantial errors in the heuristic expression used by BM to extend the
Kramers expressions beyond the hydrogenic case. Here we present the
relevant corrected expressions and show the key modified results. We
conclude that, in most cases, NTR emission was overestimated by a
factor of 1-8 by BM but is typically still large enough (as much
as 20-30% of the total emission) to be very important for electron
spectral inference and detection of electron spectral features such as
low energy cut-offs since the recombination spectra contain sharp
edges. For extreme temperature regimes and/or if the Fe abundance
were as high as some values claimed, NTR could even be the dominant
source of flare HXRs, reducing the electron number and energy budget,
problems such as in the extreme coronal HXR source cases reported by
e.g. Krucker et al.
Key words: atomic processes - Sun: corona - Sun: flares - Sun: X-rays, gamma rays - errata, addenda
1 Summary
Brown & Mallik (2008,2009) (BM) recently argued that, for hot sources, recombination of non-thermal electrons (NTR) onto highly ionised heavy ions is not negligible compared to non-thermal bremsstrahlung (NTB) as a source of flare hard X-rays (HXRs) and so should be included in modelling non-thermal HXR flare emission. They further claimed that, in some cases, NTR can be much larger than NTB with important consequences for flare physics. In view of major discrepancies between BM results for the thermal continua and those of the Chianti code (e.g. Dere et al. 2009) and of RHESSI (Lin et al. 2002) solar data, we critically re-examined the BM analysis and discovered substantial errors in the heuristic expression used by BM to extend the Kramers expressions beyond the hydrogenic case. Here we summarise the main resulting modifications to their equations and results (now validated against detailed calculations) and their conclusions concerning the importance of NTR. The BM results are correct for NTR onto Fe 26+ and a factor of 2 too high for Fe 25+ so that, at high enough T >40 MK for these to exist, NTR does strongly dominate NTB in the deka-keV range. However, at such T, thermal continuum dominates NTR and NTB in this energy range unless the non-thermal electron density is a very large fraction,![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8103efg1}
\end{figure}](/articles/aa/full_html/2010/07/aa8103e-07/Timg13.png)
|
Figure 1:
The revised thermal model spectra (dot-dash blue is TB; thick
solid red is TR) compared with Chianti's (thin solid green for TB;
dashed black for TR) at T=20 MK. Also included is the erroneous TR
spectrum (thin dashed red) from Brown & Mallik (2008). The major
discrepancy caused by the Fe edges in BM have been suitably resolved in
our revision. The smaller discrepancies are due to differences in the
Kramers' and measured cross-sections as well as the possibility of
recombination to higher levels than
|
| Open with DEXTER | |
2 Amended equations and results
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8103efg2}
\end{figure}](/articles/aa/full_html/2010/07/aa8103e-07/Timg14.png)
|
Figure 2:
Thin-target NTR:NTB ratio for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8103efg3a}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8103efg3b}
\end{figure}](/articles/aa/full_html/2010/07/aa8103e-07/Timg15.png)
|
Figure 3:
The revised thin-target spectra for 2 different temperatures
with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8103efg4}
\end{figure}](/articles/aa/full_html/2010/07/aa8103e-07/Timg16.png)
|
Figure 4:
Regime plot with our revised model showing the relevant areas
of importance in the
|
| Open with DEXTER | |
The core error in BM was their use, in the Kramers cross section and
edge energies, of quantum number m=1 for the first unfilled
level instead of its principal quantum number n. For Fe 26+ and 25+,
n=m=1, but for Fe 24+ to Fe 17+, for example, ![]() but =2.
In ionic species which already have 2-9 electrons present, the
smallest n value
but =2.
In ionic species which already have 2-9 electrons present, the
smallest n value
![]() is 2, and for 10 or more electrons,
it is
is 2, and for 10 or more electrons,
it is
![]() and so on. (Recombination rates to levels with
and so on. (Recombination rates to levels with
![]() still fall off as 1/n3, so are rather small in
comparison). The consequences of this BM error are:
still fall off as 1/n3, so are rather small in
comparison). The consequences of this BM error are:
- since, for typical hot flare temperatures of 20-30 MK, Fe 24+
and Fe 23+ are the most abundant Fe ions,
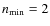 ,
not 1, and
the magnitude of the recombination emission is down compared to BM by a
factor of around
,
not 1, and
the magnitude of the recombination emission is down compared to BM by a
factor of around
 ;
;
- the recombination edges for these species are no longer at
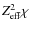 ,
or
,
or
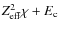 in the presence of a low energy cut-off
in the presence of a low energy cut-off
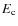 ,
but at
,
but at
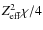 or
or
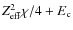 respectively;
respectively;
- additionally, the Kramers formula applies to recombination into an empty shell. For partially filled n-shells, a ``vacancy factor'', pn, has to be applied. If all recombinations to that level had equal rate, pn would be Nv/Nn, where Nn = 2n2is the total electron occupation number of the shell and Nvthe number of states unoccupied - e.g. for a He-like ion, p1=1/2while for a partially filled n=2 shell, N2=8. However, recombination into n=2 in the Kramers formula is actually dominated by the 6 p-states, at the electron energies of interest here so we can take N2 = 6and Nv the number of unoccupied 2p states, i.e. p2 = 1 for Li and Be-like initial ions and p2 = 5/6, 4/6, ... 1/6 for B- through F-like initial ions. Comparisons of such modified Kramers cross sections have been made with the results of detailed calculations using the AUTOSTRUCTURE code (cf. Badnell 2006) for initial H-like through to F-like Fe ions and agreement to within 20% was obtained for our new results using this estimate.
Table 1:
Significance of Fe 25+ and 26+ at 4 different temperatures for
![]() keV and
keV and ![]() .
.
for the cut-off power law F(E) and with
The revised thermal recombination expression (from Eq. (B.5) of Brown & Mallik 2008) as a function of photon energy
![]() is:
is:
The thick-target NTR expression (revised from Eq. (B.12) of Brown & Mallik 2008) is (power-law case):
(Thick target results are for the total emission rates over continuously injected electron collisional lifetimes). Note that Eqs. (1) and (3) also correct the following typos in Eqs. (B.2) and (B.12) of Brown & Mallik (2008):
- the term
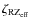 was accidentally put outside the
was accidentally put outside the 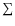 in Eq. (B.2) of BM.
in Eq. (B.2) of BM.
- it should be
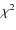 in the numerator for Eq. (B.2) of BM and not just
in the numerator for Eq. (B.2) of BM and not just 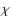 .
.
- the terms
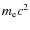 in the numerator and
in the numerator and
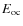 in the denominator of Eq. (B.12) of BM do not actually exist and were erroneously carried over from some other formulae.
in the denominator of Eq. (B.12) of BM do not actually exist and were erroneously carried over from some other formulae.
The ionisation equilbrium used was a fit to the standard steady state coronal collisional ionisation, optical depths being negligible. In Table 1, we have listed the abundances and
We gratefully acknowledge the financial support of a UK STFC Rolling Grant (JCB), of a Dorothy Hodgkin's Scholarship (PCVM), an ISSI Grant (JCB), and an STFC Grant (NRB). Discussions with E.P. Kontar, R.A. Schwartz, and E. Landi were invaluable in drawing attention to problems with the BM results. We are grateful to the referee in helping us condense and improve our report of the amendments.
References
- Arnaud, M., & Raymond, J. 1992, ApJ, 398, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2006, ApJS, 167, 334 [Google Scholar]
- Brown, J. C., & Mallik, P. C. V. 2008, A&A, 481, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. C., & Mallik, P. C. V. 2009, ApJ, 697, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P., Landi, E., Young, P. R., et al. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldman, U., Dammasch, I., Landi, E., & Doschek, G. A. 2004, ApJ, 609, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Wuelser, J.-P., Vourlidas, A., et al. 2008, 12th European Solar Physics Meeting, Freiburg, Germany, held September, 8-12, http://espm.kis.uni-freiburg.de/, 2.84, 12, 2 [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Mallik, P. C. V. 2010, Ph.D. Thesis, University of Glasgow [Google Scholar]
All Tables
Table 1:
Significance of Fe 25+ and 26+ at 4 different temperatures for
![]() keV and
keV and ![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8103efg1}
\end{figure}](/articles/aa/full_html/2010/07/aa8103e-07/Timg13.png)
|
Figure 1:
The revised thermal model spectra (dot-dash blue is TB; thick
solid red is TR) compared with Chianti's (thin solid green for TB;
dashed black for TR) at T=20 MK. Also included is the erroneous TR
spectrum (thin dashed red) from Brown & Mallik (2008). The major
discrepancy caused by the Fe edges in BM have been suitably resolved in
our revision. The smaller discrepancies are due to differences in the
Kramers' and measured cross-sections as well as the possibility of
recombination to higher levels than
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8103efg2}
\end{figure}](/articles/aa/full_html/2010/07/aa8103e-07/Timg14.png)
|
Figure 2:
Thin-target NTR:NTB ratio for
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{8103efg3a}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{8103efg3b}
\end{figure}](/articles/aa/full_html/2010/07/aa8103e-07/Timg15.png)
|
Figure 3:
The revised thin-target spectra for 2 different temperatures
with
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{8103efg4}
\end{figure}](/articles/aa/full_html/2010/07/aa8103e-07/Timg16.png)
|
Figure 4:
Regime plot with our revised model showing the relevant areas
of importance in the
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



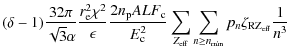
![$\displaystyle \times
\left[\frac{\epsilon - V_{\rm Z_{\rm eff}}/n^2}{E_{\rm c}} \right]^{-\delta -
1} ~~ ; ~~ \epsilon \geq E_{\rm c} + V_{\rm Z_{\rm eff}}/n^2$](/articles/aa/full_html/2010/07/aa8103e-07/img49.png)