| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 7 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202347302 | |
| Published online | 08 November 2023 | |
Theoretical investigation of electron capture processes in slow O7+–H collisions
1
Faculty of foundation, Space Engineering University,
1 Bayi Road, Huairou District,
Beijing
101416, PR China
2
Data Center for High Energy Density Physics, Institute of Applied Physics and Computational Mathematics,
PO Box 8009,
6 Huayuan Road, Haidian District,
Beijing
100088, PR China
e-mail: wu_yong@iapcm.ac.cn; liu_ling@iapcm.an.cn
3
HEDPS, Center for Applied Physics and Technology, Peking University,
22 Huaqing Jiayuan, Chengfu Road, Zhongguancun Street, Haidian District,
Beijing
100084, PR China
4
School of Physics, Beijing Institute of Technology,
5 Zhongguancun South Street, Haidian District,
Beijing
100081, PR China
5
Institute of Environmental Science, Shanxi University,
92 Wucheng Road, Taiyuan City
030006,
Shanxi, PR China
6
Department of Physics, College of Science, Qiqihar University,
42 Wenhua Street, Jianhua District, Qiqihar City
161006,
Heilongjiang Province, PR China
Received:
27
June
2023
Accepted:
9
September
2023
Aims. The total and n-, l-, and S -resolved single-electron-capture cross sections for the collisions of O7+ with atomic hydrogen are studied in the energy region from 10−3eV u−1−5keV u−1.
Methods. These state-selective cross sections were calculated by employing the full quantum-mechanical molecular-orbital close-coupling (QMOCC) method. The ab initio multireference single- and double-excitation configuration interaction approach, with optimized atomic basis sets to accurately describe the highly excited states, was used to obtain the adiabatic potentials and the radial and rotational coupling matrix elements that are required in the QMOCC calculation.
Results. Our results are compared with other available theoretical and experimental data. The n = 5 manifold is the dominant reaction channel for the chasrge-transfer process for this collision system over the entire energy range, and our results agree better with the experimental data than the other theoretical results in the energy region in which they overlap because we included the necessary highly excited states in the expansion basis set. These charge-exchange cross-section data are useful for understanding and modeling the X-ray emission in astrophysical environments.
Key words: solar wind / atomic data / scattering
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Collisions between highly charged ions and neutral species have been extensively studied in various fields, such as astrophysics and fusion-plasma diagnostics. In an astrophysical environment, electron-capture processes resulting from highly charged ions colliding with the neutral atoms or molecules are very important for explaining the celestial phenomena (Zhang et al. 2023, 2022; Wu et al. 2012; Lin et al. 2019). For example, the formation of solar wind X-rays and the extreme ultraviolet can be attributed to the electron-capture collisions of fast solar wind ions with neutral ambient gases (Wu et al. 2012). The solar wind is composed of electrons, protons, alpha particles, and a large number of other highly charged ions, such as Cq+, Nq+, Oq+, Sq+, Neq+, Mgq+, Alq+, Siq+, and Arq+. The types of neutral particles are different in different astrophysical environments. For instance, the atmosphere of a comet contains H2O, CO, HO2, and their dissociation products H2, H, O, and so on, the heliosphere mainly contains H and He, the geocorona mainly contains H, and the halo of Mars mainly contains H and O. Therefore, it is crucial to investigate highly charged solar wind ions colliding with these neutral particles. Moreover, the obtained cross-section data and rate coefficients can also provide insights into the research of X-ray simulations of the solar wind.
With the continuous advancement of science and technology, various space equipments have appeared in succession, such as the Chandra X-ray Observatory, the XMM-Newton detector, the far-ultraviolet spectroscopic detector (FUSE), and the Suzaku satellite. The soft x-ray and extreme-ultraviolet emission of the objects from the Solar System have been observed using these space equipments. For example, in 2006, Chandra detected X-rays from Venus, which revealed that the Venusian halo X-rays originated from a charge-exchange mechanism of the solar wind (Dennerl 2009). Moreover, the XMM-Newton detector has observed soft X-rays (0.2–2 keV) from the auroral region of Jupiter, and it was found that these X-rays originated from the charge-transfer processes between highly charged solar wind ions (Oq+, Cq+, and Neq+) and neutral particles from the Jupiter atmosphere (Krasnopolsky & Mumma 2001; Cravens 1997). Similarly, the soft X-rays from Mars have been observed by XMM-Newton (Bhardwaj et al. 2009), and it was confirmed that the charge-exchange process of highly charged solar wind ions (Cq+, Nq+, Oq+, and Neq+) colliding with neutral particles in the atmosphere or outer atmosphere are the origin of this emission. These X-rays are important for diagnosing the composition, evolution, velocity, and distribution of the neutral gas density in the solar wind.
We study the electron-capture process in collisions of O7+ ions with atomic hydrogen in the energy region 0.001 eV u−1– 5 keV u−1 using the full quantum-mechanical molecular-orbital close-coupling (QMOCC) method. To the best of our knowledge, the available experimental and theoretical data for this collision system have been very limited so far. Total charge-transfer cross sections have been measured by Zhang et al. (2022), Meyer et al. (1985), Panov et al. (1983), and Havener et al. (in prep.) in the combined energy region 10 eV u−1–7 keV u−1. State-selective charge-transfer measurements in this collision system have only been performed by Kearns et al. (2003) for n = 3–5 channels of O7+ ions in the energy range 875–350 eV u−1. On the theoretical side, Phaneuf et al. (1987) and Janev et al. (1988) have provided the recommended total charge-transfer cross sections for this collision system in the energy region 180 eV u−1–400 keV u−1. In addition, Nolte et al. (2011) have used the MOCC (the quantum molecular orbital close-coupling method), AOCC (the atomic orbital close-coupling method), and CTMC (the more sophisticated classical trajectory Monte Carlo technique) methods to calculate the total and n(n = 4,5)-, l-, and S-resolved charge-transfer cross section of collisions between O7+ ions and H atoms in the energy region 10−2–105 eV u−1, but their results remain unpublished so far. The main motivation of our work is to investigate the electron-capture dynamics of O7+–H collisions in the energy region 0.001 eV u−1–5 keV u−1 and provide the accurate total and state-selective electron-capture cross-section data in a wide energy region for this collision system. The QMOCC method is employed to calculate the total, n-resolved, nl-resolved, and nls-resolved charge-transfer cross sections. The potentials curves and matrix elements that are required in the scattering calculation are obtained by the ab initio multireference single- and double-excitation configuration interaction (MRDCI) method.
2 Theoretical methods
2.1 Scattering theory
We employed the QMOCC method, which has been described in the literature (Lin et al. 2019; Nolte et al. 2012; Zygelman et al. 1992), to calculate n-, l-, and S -resolved charge-transfer cross sections for O7+–H collision systems at low energies. In the Born–Oppenheimer (B–O) approximation, the total wave functions can be expanded in terms of adiabatic electronic wavefunctions ψi(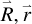 ),
),
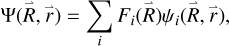 (1)
(1)
where 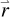 and
and 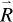 are the electron position vector and internuclear distance vector in the body-fixed frame, respectively. The Schrödinger equation can be shown as
are the electron position vector and internuclear distance vector in the body-fixed frame, respectively. The Schrödinger equation can be shown as
![$\left[ {\nabla _R^2\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over I} - 2\mu \left( {u - E} \right)} \right]F\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} } \right) = \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over M} \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} } \right) + \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over P} \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} } \right) \bullet {\nabla _R}} \right)F\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over R} } \right),$](/articles/aa/full_html/2023/11/aa47302-23/aa47302-23-eq5.png) (2)
(2)
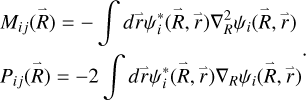 (3)
(3)
in which I and u are the unit matrix and diagonal adiabatic potential matrix. M and P are coupling matrices.
Inserting Eq. (1) into Eq. (2), we obtain
![$\matrix{ {\left[ {{{{{\rm{d}}^2}} \over {{\rm{d}}{R^2}}} - {{J\left( {J + 1} \right) - {\lambda ^2}} \over {{R^2}}} - 2\mu \left( {u\left( R \right) - E} \right)} \right]{f^J}\left( R \right)} \hfill \cr {\quad = \left( {{V^R}\left( R \right) + {V^C}\left( R \right)} \right){f^J}\left( R \right),} \hfill \cr } $](/articles/aa/full_html/2023/11/aa47302-23/aa47302-23-eq7.png) (4)
(4)
![$\matrix{ {V_{ij}^R\left( R \right) = \left[ {\left\langle {i\left| { - {{{\partial ^2}} \over {\partial {R^2}}} + {{L_x^2 + L_y^2} \over {{R^2}}}} \right|j} \right\rangle - 2\left\langle {i\left| {{\partial \over {\partial R}}} \right|j} \right\rangle {\partial \over {\partial R}}} \right]{\delta _{{\lambda _i}{\lambda _j}}}} \hfill \cr {V_{ij}^C\left( R \right) = - 2{\delta _{{\lambda _i}{\lambda _j} + 1}}{1 \over {{R^2}}}\left[ {{{\left[ {\left( {J - {\lambda _i}} \right)\left( {J + {\lambda _i} + 1} \right)} \right]}^{1/2}}{{\left\langle {i\left| {i{L_y}} \right|j} \right\rangle } \over {{R^2}}}} \right]} \hfill \cr {\quad \quad \quad \,\,\, + 2{\delta _{{\lambda _i}{\lambda _j} - 1}}{1 \over {{R^2}}}\left[ {{{\left[ {\left( {J + {\lambda _i}} \right)\left( {J - {\lambda _i} + 1} \right)} \right]}^{1/2}}{{\left\langle {i\left| {i{L_y}} \right|j} \right\rangle } \over {{R^2}}}} \right],} \hfill \cr } $](/articles/aa/full_html/2023/11/aa47302-23/aa47302-23-eq8.png) (5)
(5)
in which VR and VC represent the radial and rotational coupling matrices. 〈i|…| j〉 represents 〈ψi |…| ψj〉, J is the total angular momentum, Ly is the y-component of the electronic angular momentum, and λj is the elements of the diagonal matrix λ.
For convenience, fJ(R) is usually defined as
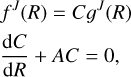 (6)
(6)
in which C is the orthogonal transformation matrix and satisfies the boundary condition 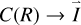 ; R → ∞. In this case, the coupled Eq. (4) are replaced by
; R → ∞. In this case, the coupled Eq. (4) are replaced by
![$\matrix{ {\left[ {{{{{\rm{d}}^2}} \over {{\rm{d}}{R^2}}} - {{J\left( {J + 1} \right) - {\lambda ^2}} \over {{R^2}}} + 2\mu E} \right]g_\gamma ^J - 2\mu \sum\limits_{\gamma '} {{U_{\gamma \gamma '}}} \left( R \right)g_{\gamma '}^J = 0} \hfill \cr {{U_{\gamma \gamma '}}\left( R \right) \equiv {{\left[ {C\left( {u - P} \right){C^{ - 1}}} \right]}_{\gamma \gamma '}}} \hfill \cr } ,$](/articles/aa/full_html/2023/11/aa47302-23/aa47302-23-eq11.png) (7)
(7)
where U and P represent the diabatic radial and rotational coupling matrices, respectively. Solving the equations by using the multichannel log-derivative method of Johnson (1973), we can obtain the K matrix and S matrix as
![$S = \left[ {I + iK} \right]{\left[ {I - iK} \right]^{ - 1}}.$](/articles/aa/full_html/2023/11/aa47302-23/aa47302-23-eq12.png) (8)
(8)
The electron-capture cross section from state i to j can be obtained as
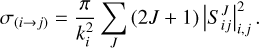 (9)
(9)
Finally, the electron translation factors (ETFs), which are important for the collision energies above 1 keV u−1, are used to consider the translation effects in the collision dynamics. The radial and rotational coupling matrix elements between the states and can be transformed into
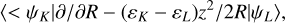 (10)
(10)
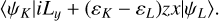 (11)
(11)
These modifications are similar to the common ETFs approach of reference (Errea et al. 1982). In these equations, εK and εL represent the electronic energies of states ψK and ψL, respectively. z2 and zx represent the components of quadrupole moment tensor.
Asymptotic separated-atom energies of the singlet of O7+−H.
2.2 Molecular structure calculations
We employed the MRDCI method (Buenker et al. 2014; Krebs & Buenker 1995) to calculate the adiabatic potentials and coupling matrix elements for the O7+−H scattering system. For the O7+ ion, we used a hybrid basis set consisting of two components (Wu et al. 2012, 2011; Dunning 1989): (i) the standard Dunning neutral atom basis, and (ii) a one-electron basis of hydrogenlike orbitals. In order to describe the Rydberg states of oxygen atoms exactly, a large Gaussian basis set (17s, 12p, 9d, 6f, and 3g) was optimized and used. We also employed a 6s, 5p, 4d, and 5f basis set contracted to 4s, 3p, 2d, and 1f for hydrogen. We obtained adiabatic potentials and couplings of the O7+−H scattering system for internuclear distances between 1.0 and 50 au with the full configuration interaction calculation. For the singlet states, 21 1Σ+,9 1∆, and 2 1Γ electronic states in 1A1 symmetry, and 14 1Π and 5 1Φ electronic states in 1B1 symmetry were obtained. For the triplet states, 20 3Σ+, 9 3∆, and 2 3Γ electronic states in 3A1 symmetry, and 14 3Π and 5 3Φ electronic states in 3B1 symmetry were obtained. In Tables 1 and 2, the energies of the considered states in the asymptotic region are shown and compared with the available data from the National Institute of Standards and Technology (NIST; Kramida et al. 2022). The entries marked with an asterisk indicate theoretical results obtained using the Grasp program, as the experimental results have not been reported. The largest error in the relative asymptotic energies of the [OH]7+ system is smaller than 0.1 eV. This accuracy of the energies is quite adequate for the scattering calculations.
Asymptotic separated-atom energies of the triplet of O7+−H.
3 Results and discussion
3.1 Potentials and couplings
Figures 1a and 2a show the adiabatic potential energy curves of [OH]7+ or the singlet and triplet states, respectively, in the range of internuclear distance from 1 au to 50 au. The 211 Σ+ and 20 3Σ+ represent the initial state O7+−H(1s). The regions of the avoided crossings for the important n = 5 and 6 channels are displayed in Figs. 1b and 2b. Some avoided crossings existed between the initial channel and the final n = 5, 6 channels in the region of internuclear distance R = 10.00–15.00 au and R = 30.00–35.00 au, respectively. The avoided crossings in the region of R = 10.00–15.00 au play a major role in the charge-transfer process. These avoided crossings of the potential energy curve were also found in previous studies for the collisions of highly charged ions with H atoms (Shipsey et al. 1981; Nolte et al. 2012; Lin et al. 2019). Therefore, the n = 5 channel will become the dominant channel for the charge-transfer process for this collision system.
Radial and rotational coupling elements were computed with the finite-difference method (Hirsch et al. 1980). In Figs. 3 and 4, radial coupling matrix elements between the adjacent channels for the dominant n = 5 manifold and some mainly rotational coupling matrix elements which considered the influence of ETFs are displayed as a function of internuclear distance R. Figure 3 shows that for the nuclear distance R < 15.00 au, there are some relatively strong and sharp peaks between the initial and n = 5 channels that originated from the avoided crossings of the potential energy curve in the corresponding region. Around R ~ 12.00 au, a strong and broad coupling exists between the 111Σ+ and 121∑+ states and 103∑+ and 113∑+ states. This coupling suggests the primary gateway of electron charge-transfer flux toward the final states.
 |
Fig. 1 Adiabatic potential curves of the singlet of O7+−H system. 2–21 1Σ+ and l–l41Π+ states correspond to the O6+(ls2s) + H+, O6+(ls2p) + H+, O6+(ls3s) + H+, O6+(ls3d) + H+, O6+(ls3p) + H+, O6+(ls4s) + H+, O6+(ls4d) + H+, O6+(ls4f) + H+, O6+(ls4p) + H+, O6+(ls5s) + H+, O6+(ls5g) + H+, O6+(ls5f) + H+, O6+(ls5d) + H+, O6+(ls5p) + H+, O6+(ls6s) + H+, O6+(ls6g) + H+, O6+(ls6f) + H+, O6+(ls6d) + H+, O6+(ls6p) + H+, and O7++H(ls) channels in the asymptotic region. |
3.2 Electron-capture cross sections
In our QMOCC calculations, a large expansion basis set was used that consisted of 69 1,3∑+ and 1,3Π states, correlating with the n = 2, 3, 4, 5, and 6 atomic manifolds of O6+ ions. The total and n-, l-, and S -resolved electron-capture cross sections were calculated in the energy range 10−3 eV u−−5.0 keV u−1. Our cross section results were systematically compared with previous theoretical and experimental results. In the MOCC calculations by Nolte et al. (2011), a Gaussian basis set that contained 17s, lip, 9d, 6f, and 3g states was used on O7+ and a 6s, 3p, 2d, and If basis contracted to 4s, 3p, 2d, and If was used on H in their MRDCI calculation. Their largest error for the relative asymptotic energies of [OH]7+ system is about 0.06629 au (≈ 1.804 eV). This accuracy of the energies will produce certain errors in the subsequent scattering calculations. In their MOCC calculation, 37 1,3∑ and 1,3n states were considered in the expansion basis, correlating with the n = 4, 5 atomic manifolds. The contributions from n = 2, 3, 6 atomic manifolds to the scattering cross sections were ignored.
We compare in Fig. 5 our total charge-transfer cross sections of the QMOCC calculation with the available experimental (Panov et al. 1983; Meyer et al. 1985; Zhang et al. 2022) and other theoretical (Phaneuf et al. 1987; Janev et al. 1988; Nolte et al. 2011) results in the energy range from 0.001 to 5000 eV u−1. Our QMOCC results agree well with the experimental results of Zhang et al. (2022) and Meyer et al. (1985) in the overlapping energy regions, and they lie closer to the AOCC results of Nolte et al. (2011) and the recommended results of Janev et al. (1988) in the energy range 100–5000 eV u−1. For energies below 20 eV u−1, our results are significantly lower than the experimental data of Zhang et al. (2022), and the MOCC results of Nolte et al. (2011) are closer to the experimental data than ours. However, in the energy region 20–1000 eV u−1, our QMOCC results agree better with the experimental data of Zhang et al. (2022), mainly because more highly excited states are taken into account in our molecular structure and scattering cross-section calculation.
The singlet and triplet n-resolved QMOCC charge-transfer cross sections for the O7+−H system are shown in Figs. 6a and b, respectively. To the best of our knowledge, no other experimental or theoretical studies of n-resolved cross sections for electrons captured to the singlet and triplet final states for this collision system have been published so far. The n = 5 manifold clearly is the dominant path for charge transfer in the entire energy range. Figure 6a shows that when the energy is higher than 30 eV u−1, the n = 6 manifold becomes the subdominant reaction channel for the charge-transfer process. In the energy range from 3 to 30 eV u−1, the n = 4 manifold is the subdominant path for the charge-transfer process. For energies lower than 3 eV u−1, the n = 3 manifold is more important. Figure 6b also shows that the n = 6 manifold is the subdominant path for the charge-transfer process in the energy range from 20 to 1500 eV u−1. For energies higher than 1500 eV u−1 or lower than 20 eV u−1, the n = 4 manifold is the subdominant charge-transfer path.
The total n-resolved charge-transfer cross sections for O7+−H system, compared with the previous MOCC and AOCC results of Nolte et al. (2011), are shown in Fig. 7. This figure shows that n = 5 is the dominant reaction channel in the considered energy range for this collision system. Our QMOCC results agree better with the previous MOCC results of Nolte et al. (2011) than with the AOCC results (Nolte et al. 2011) in the overlapping energy region for capture to the n = 5 shells of O6+ ions. The AOCC cross sections (Nolte et al. 2011) have the same energy behavior as our results, but the magnitudes are slightly lower than ours. For the subdominant channels n = 4, our results also agree well with the MOCC results of Nolte et al. (2011) in the overlapping energy region. However, the AOCC results (Nolte et al. 2011) are larger than our results in the energy region below about 3 keV u−1. For the weakly coupled reaction channels n = 3 and n = 6, our QMOCC results are comparable with the AOCC results (Nolte et al. 2011) at the collision energy of 0.2 keV u−1 and 5 keV u−1, respectively. For other energies, there are significant differences between our results and those of the AOCC (Nolte et al. 2011). This difference may arise because we neglected the contribution of the molecular states with higher angular momentum (e.g., Δ, Φ, and Γ) to the charge-transfer cross sections.
The total nl-resolved QMOCC charge-transfer cross sections for O7+−H system are displayed in Fig. 8. In Figs. 9 and 10, we show our singlet and triplet nl-resolved charge-transfer cross sections for the O7+−H system, respectively. They are compared with the previous MOCC results (Nolte et al. 2011). As observed in Fig. 8, the 5s is the dominant charge-transfer path in the energy range 3–1000 eV u−1 for this collision system. For energies lower than ~ 3 eV u−1 or higher than ~1000 eV u−1, charge transfer to the 5p state becomes more important. Figure 9 shows that electron capture to the 5f state of O6+ ions becomes the dominant singlet state in the energy regions below ~2 eV u−1 and 200– 1000 eV u−1. However, 5s becomes the dominant singlet state in the energy regions above ~1000 eV u−1 and 2–200 eV u−1. Figure 10 shows that for energies lower than ~10 eV u−1 and higher than ~800 eV u−1, electron capture to the 5p state of O6+ ions becomes the dominant triplet channel. In the energy region of 10–800 eV u−1, electron capture to the 5s state becomes the dominant triplet channel. Due to the effect of the value and statistical weight of the singlet and triplet cross sections, this difference is not reflected in the total nl-resolved cross sections. This figure also shows large differences between our results and the MOCC results of Nolte et al. (2011) for the 5d and 5g singlet states. Especially for low collision energies, our QMOCC cross sections are significantly lower than those of the MOCC method. Moreover, our results for 5p singlet states are also clearly smaller than those of the MOCC method in the energy region below about 60 eV u−1. The difference between our QMOCC results and the MOCC results (Nolte et al. 2011) may arise from two facts: (1) The influence of the n = 6 states of O6+ ions are neglected in the MOCC calculations (Nolte et al. 2011), and (2) the difference in the number of radial and rotational couplings and their strengths and positions for the corresponding internuclear distance.
Figure 11 presents the triplet-singlet ratios for nl-resolved cross sections for O7+−H. Previous studies (Nolte et al. 2011; Greenwood et al. 2001; Bliek et al. 1998) have shown that the triplet-to-singlet ratio forcharge-transfercross sections is related to the impact energy for the collisions between highly charged ions and the neutral particles. This ratio approaches 3:1 forcollision energies higher than 10 keV u−1. This figure shows that only a few triplet-to-singlet ratios for n, l-resolved cross sections seem to approach 3:1. Most ratios deviate from 3 and vary widely in the considered collision energy range. This deviation may be caused by the strong dependence of the triplet-singlet ratios on the impact energy in the low collision energy region, which approaches a statistical distribution only at higher energies.
 |
Fig. 2 Adiabatic potential curves of the triplet of O7+−H system. 2–203Σ+ and 1–143Π+ states correspond to the O6+(ls2s) + H+, O6+(ls2p) + H+, O6+(ls3s) + H+, O6+(ls3d) + H+, O6+(ls3p) + H+, O6+(ls4s) + H+, O6+(ls4d) + H+, O6+(ls4f) + H+, O6+(ls4p) + H+, O6+(ls5s) + H+, O6+(ls5g) + H+, O6+(ls5f) + H+, O6+(ls5d) + H+, O6+(ls5p) + H+, O6+(ls6s) + H+, O6+(ls6g) + H+, O6+(ls6f) + H+, O6+(ls6d) + H+, O6+(ls6p) + H+, and O7++H(ls) channels in the asymptotic region. |
 |
Fig. 3 Radial couplings for the dominant n = 5 channels for both 1,3∑+ and1,3 ∏+ states. |
 |
Fig. 4 Rotational coupling matrix elements for [OH]7+. |
 |
Fig. 5 Total charge-transfer cross sections in O7+−H collisions. |
 |
Fig. 6 Panel a: Singlet n-resol·ved QMOCC cross sections for [OH]7+. Panel b: Triplet n-resolved QMOCC cross sections for [OH]7+. |
 |
Fig. 7 Total n-resolved QMOCC cross sections for [OH]7+. |
 |
Fig. 8 Total nl-resolved QMOCC cross sections for [OH]7+. |
 |
Fig. 9 Singlet nl-resolved QMOCC cross sections for [OH]7+. |
 |
Fig. 10 Triplet nl-resolved QMOCC cross sections for [OH]7+. |
 |
Fig. 11 Triplet-singlet ratios for nl-resolved cross sections for O7+−H. |
4 Summary
Highly charged solar wind ions colliding with neutral particles play an important role in the research of solar wind X-ray simulations. In the present work, the full quantum-mechanical molecular-orbital close-coupling (QMOCC) method was used to calculate the charge-transfer cross sections for the collision system O7+−H. The adiabatic potentials and coupling data used in the QMOCC calculations were carried out through the ab initio multireference single- and double-excitation configuration interaction (MRDCI) approach. In our QMOCC calculations, total and n, l and S-resolved cross sections for single-electron capture to the n = 2, 3, 4, 5, 6 states of O6+ ions were studied in the energy range 10−3 eV u−1−5.0 keV u−1. Throughout the entire energy range, the n = 5 manifold is the dominant charge-transfer channel for this collision system. By comparing with the existing experimental and theoretical data, we found that our results agree better with the experimental data than with the other theoretical results in the considered energy region. There are certain differences between our results and previous QMOCC results (Nolte et al. 2011) in the overlapping energy region. The discrepancy is mainly due to the following reasons: (i) The differences in the sizes of the expansion bases used in the molecular structure calculations, (ii) the differences in the accuracy of the energies in the respective asymptotic energies of the [OH]7+ system, and iii) a greater number of highly excited states are considered in our QMOCC calculation.
Acknowledgements
This work was supported by the National Key Research and Development Program of China (Grants No. 2022YFA1602500) and National Natural Science Foundation of China (Grants Nos. 11934004, 12274040, 12203106, 12204288, 11474032, 11534011 and U1530261).
References
- Bhardwaj, A., Eisner, R. F., Gladstone, G. R., et al. 2009, Advances in Geosciences, 15: Planetary Science (PS), 229 [Google Scholar]
- Bliek, F. W., Woestenenk, G. R., Hoekstra, R., & Morgenstern, R. 1998, Phys. Rev. A, 57, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Buenker, R. J., Phillips, R. A., Krebs, S., et al. 2014, Theor. Chem. Acc., 133, 1468 [CrossRef] [Google Scholar]
- Cravens, T. E. 1997, Geophys. Res. Lett., 24 [Google Scholar]
- Dennerl, K. 2009, X-Rays from Nonmagnetic Planets (Advances in Geosciences, 15: Planetary Science (PS)), 53 [Google Scholar]
- Dunning, T. H. 1989, J. Chem. Phys., 90 [Google Scholar]
- Errea, L. F., Mendez, L., & Riera, A. 1982, J. Phys. B At. Mol. Phys., 15, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Greenwood, J. B., Williams, I. D., Smith, S. J., & Chutjian, A. 2001, Phys. Rev. A, 63, 062707 [NASA ADS] [CrossRef] [Google Scholar]
- Hirsch, G., Bruna, P. J., Buenker, R. J., & Peyerimhoff, S. D. 1980, Chem. Phys., 45, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Janev, R., Phaneuf, R., & Hunter, H. 1988, Atom. Data Nuclear Data Tables, 40, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, B. R. 1973, J. Comput. Phys., 13, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Kearns, D. M., Mccullough, R. W., Trassl, R., & Gilbody, H. B. 2003, J. Phys. B At. Mol. Opt. Phys., 36, 3653 [NASA ADS] [CrossRef] [Google Scholar]
- Kramida, A., Ralchenko, Y., Reader, J., & NIST ASD Team 2022, NIST Atomic Spectra Database (ver. 5.10), [Online]. Available: https://physics.nist.gov/asd [2023, April 27] (Gaithersburg, MD: National Institute of Standards and Technology) [Google Scholar]
- Krasnopolsky, V. A., & Mumma, M. J. 2001, ApJ, 549, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Krebs, S., & Buenker, R. J. 1995, J. Chem. Phys., 103, 5613 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, X., Wu, Y., Wang, J., Shao, B., & Janev, R. 2019, A&A, 625, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, F. W., Howald, A. M., Havener, C. C., & Phaneuf, R. A. 1985, Phys. Rev. A, 32, 3310 [NASA ADS] [CrossRef] [Google Scholar]
- Nolte, J. L., Wu, Y., Stancil, P. C., Buenker, R. J., & Havener, C. C. 2011, Unpublished, See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/258482138 [Google Scholar]
- Nolte, J. L., Stancil, P. C., Liebermann, H. P., Buenker, R. J., & Schultz, D. R. 2012, J. Phys. B At. Mol. Opt. Phys., 45, 245202 [NASA ADS] [CrossRef] [Google Scholar]
- Panov, M. N., Basalaev, A. A., & Lozhkin, K. O. 1983, Physica Scripta, 1983, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Phaneuf, R. A., Janev, R. K., & Pindzola, M. S. 1987, Atomic Data for Fusion, 5 [Google Scholar]
- Shipsey, E. J., Browne, J. C., & Olson, R. E. 1981, J. Phys. B At. Mol. Opt. Phys., 14, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Stancil, P. C., Liebermann, H. P., et al. 2011, Phys. Rev. A, 84, 022711 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Stancil, P. C., DR Schultz, Y. Hui, H. P. L., & Buenker, R. J. 2012, J. Phys. B At. Mol. Opt. Phys., 45, 235201 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, R. T., Seely, D. G., V. M. Andrianarijaona, I. N. D., & Havener, C. C. 2022, ApJ, 931 [Google Scholar]
- Zhang, R. T., Liao, T., Zhang, C. J., et al. 2023, MNRAS, 520, 1417 [CrossRef] [Google Scholar]
- Zygelman, B., Cooper, D. L., Ford, M. J., Dalgarno, A., & Raimondi, M. 1992, Phys. Rev. A, 46, 3846 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Adiabatic potential curves of the singlet of O7+−H system. 2–21 1Σ+ and l–l41Π+ states correspond to the O6+(ls2s) + H+, O6+(ls2p) + H+, O6+(ls3s) + H+, O6+(ls3d) + H+, O6+(ls3p) + H+, O6+(ls4s) + H+, O6+(ls4d) + H+, O6+(ls4f) + H+, O6+(ls4p) + H+, O6+(ls5s) + H+, O6+(ls5g) + H+, O6+(ls5f) + H+, O6+(ls5d) + H+, O6+(ls5p) + H+, O6+(ls6s) + H+, O6+(ls6g) + H+, O6+(ls6f) + H+, O6+(ls6d) + H+, O6+(ls6p) + H+, and O7++H(ls) channels in the asymptotic region. |
| In the text | |
 |
Fig. 2 Adiabatic potential curves of the triplet of O7+−H system. 2–203Σ+ and 1–143Π+ states correspond to the O6+(ls2s) + H+, O6+(ls2p) + H+, O6+(ls3s) + H+, O6+(ls3d) + H+, O6+(ls3p) + H+, O6+(ls4s) + H+, O6+(ls4d) + H+, O6+(ls4f) + H+, O6+(ls4p) + H+, O6+(ls5s) + H+, O6+(ls5g) + H+, O6+(ls5f) + H+, O6+(ls5d) + H+, O6+(ls5p) + H+, O6+(ls6s) + H+, O6+(ls6g) + H+, O6+(ls6f) + H+, O6+(ls6d) + H+, O6+(ls6p) + H+, and O7++H(ls) channels in the asymptotic region. |
| In the text | |
 |
Fig. 3 Radial couplings for the dominant n = 5 channels for both 1,3∑+ and1,3 ∏+ states. |
| In the text | |
 |
Fig. 4 Rotational coupling matrix elements for [OH]7+. |
| In the text | |
 |
Fig. 5 Total charge-transfer cross sections in O7+−H collisions. |
| In the text | |
 |
Fig. 6 Panel a: Singlet n-resol·ved QMOCC cross sections for [OH]7+. Panel b: Triplet n-resolved QMOCC cross sections for [OH]7+. |
| In the text | |
 |
Fig. 7 Total n-resolved QMOCC cross sections for [OH]7+. |
| In the text | |
 |
Fig. 8 Total nl-resolved QMOCC cross sections for [OH]7+. |
| In the text | |
 |
Fig. 9 Singlet nl-resolved QMOCC cross sections for [OH]7+. |
| In the text | |
 |
Fig. 10 Triplet nl-resolved QMOCC cross sections for [OH]7+. |
| In the text | |
 |
Fig. 11 Triplet-singlet ratios for nl-resolved cross sections for O7+−H. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


