| Issue |
A&A
Volume 666, October 2022
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202244295 | |
| Published online | 18 October 2022 | |
Detecting chiral asymmetry in the interstellar medium using propylene oxide
1
Department of Space, Earth and Environment, Chalmers University of Technology,
Onsala Space Observatory,
439 92
Onsala, Sweden
2
Leiden Observatory, Leiden University,
Post Office Box 9513,
2300 RA
Leiden, The Netherlands
e-mail: boy.lankhaar@chalmers.se
Received:
17
June
2022
Accepted:
6
July
2022
Context. Life is distinctly homochiral. The origins of this homochirality are under active debate. Recently, propylene oxide has been detected in the gas-phase interstellar medium (ISM). The enantiomeric composition of ISM propylene oxide may be probed through circular polarization measurements, but accurate estimates of the circular dichroism properties of the microwave transitions of propylene oxide are not available.
Aims. Our aim is to develop a model of the circular dichroic activity in torsion–rotation transitions of closed-shell chiral molecules such as propylene oxide. With this model we can estimate the viability, and optimize the observation strategies, of enantiomeric excess detection in ISM propylene oxide.
Methods. Circular dichroism in spectral lines manifests through the simultaneous interaction of an electromagnetic radiation field with the molecular electric dipole moment and magnetic dipole moment. We developed techniques to quantify electric dipole and magnetic dipole moments of torsion–rotation transitions by expanding on earlier modeling of the electric and magnetic dipole properties of single torsion–rotation levels. To model the circular dichroism properties of propylene oxide, we used these techniques in combination with ab initio quantum chemical calculations.
Results. The expressions for the dichroic activity of the microwave transitions of torsionally active molecules are derived. We find that the torsional motion of molecules exhibiting internal rotation contributes significantly to the total magnetic moment. We present estimates for the dichroic activity of the torsion–rotation transitions of propylene oxide. We predict that the circular polarization fractions of emission lines of enantiopure propylene oxide relevant to astronomical detections are on the order of 10−6.
Conclusions. Due to the low predicted circular polarization fractions, we conclude that enantiomeric characterization of propylene oxide in the gas phase of the ISM is impossible with the current astronomical observation techniques. We suggest that only chiral radical species may be viably employed for purposes of enantiomeric excess detection. We estimate that laboratory experiments may be successful in detecting the enantiomeric composition of a mixture of propylene oxide through microwave dichroism spectroscopy.
Key words: astrochemistry / molecular data / polarization / ISM: molecules
© B. Lankhaar 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Homochirality is a key feature of life on Earth, and is hypothesized to be an indicator of extraterrestrial life (Avnir 2020). While the origins of the homochirality of life are under active debate (Boyd & Famiano 2018), past analyses of carbonaceous chondrites revealed chiral asymmetry in organic matter (Cronin & Pizzarello 1997), suggesting that the trait of homochirality that characterizes life on Earth might have cosmochemical origins. The recent detection of propylene oxide towards Sgr. B2(N) marked the first chiral molecule to have been discovered in the gas phase of the interstellar medium (ISM; McGuire et al. 2016). This discovery opens up the possibility of probing its possible chiral asymmetry through polarization measurements.
While the production of ISM propylene oxide is suggested to yield a racemic mixture (Bergantini et al. 2018), chiral asymmetry may be produced through chirally selective photolysis by circularly polarized electrons (Ulbricht & Vester 1962; Dreiling & Gay 2014) or circularly polarized light (Flores et al. 1977; Modica et al. 2014). A slight chiral asymmetry may be subsequently enhanced through enantioselective surface chemistry (Gellman et al. 2015). Models of the chirally selective chemistry in the ISM may be constrained if the enantiomeric composition of propylene oxide can be probed.
Enantiomeric excess may be observed through polarization measurements. The transfer of radiation through a non-racemic compound is characterized by the production of circular polarization at its transition frequencies (Eyring et al. 1968; Holzwarth et al. 1974). Chiral compounds that have an enantiomeric excess are dichroic because of the electromagnetic (EM) radiation’s simultaneous interaction with the molecular electric and magnetic dipole moment (Polavarapu 2018). Laboratory measurements of chiral compounds have successfully indicated an enantiomeric excess through the observation of circular dichroism in electronic (Eyring et al. 1968; Caldwell 1969) and vibrational (Holzwarth et al. 1974; Stephens 1985) transitions.
Propylene oxide in the ISM has been detected in its torsion–rotation transitions. While both the electronic (Turchini et al. 2004; Stranges et al. 2005; Garcia et al. 2014; Contini et al. 2007; Rizzo & Vahtras 2011) and vibrational (Polavarapu et al. 1985; Kawiecki et al. 1988; Bloino & Barone 2012) optical activity of propylene oxide have been characterized, the circular dichroism of its torsion–rotation transitions has yet to be investigated. Laboratory experiments on the optical activity of any microwave transition are yet to be performed. The circular dichroism properties of rotational transitions have been investigated theoretically (Salzman & Polavarapu 1991; Salzman 1997), but these studies did not include the contribution of molecular torsional motion to the optical activity. Determining the viability of the astronomical detection of chiral asymmetry in propylene oxide requires accurate theoretical modeling of the dichroic properties of its torsion–rotation transitions.
In this paper, we investigate the dichroic properties of the torsion–rotation transitions of propylene oxide and discuss the possibility of detecting a possible enantiomeric excess in the ISM through the partial circular polarization of propylene oxide emission. In Sect. 2, we discuss the theory behind the emergence of circular polarization in the emission of a chiral molecule characterized by enantiomeric excess. In Sect. 3, we discuss the torsion–rotation structure of propylene oxide. In addition, we outline the quantum chemical methods that we used to compute the relevant electric and magnetic properties of propylene oxide. We also present the proper theory to compute the dichroic properties of the torsion–rotation transitions of a torsionally active molecule. We present the results of our calculations in Sect. 4. In Sect. 5, we discuss the implications of the dichroic properties of the torsion–rotation transitions for astronomical searches for chiral asymmetry in the ISM gas phase. We conclude in Sect. 6.
2 Theory
We set out to evaluate the possibility of detecting enantiomeric excess in propylene oxide in the ISM through polarization observations. The astronomical emission of propylene oxide occurs in the microwave region, and is associated with torsion–rotation transitions. To characterize the production of polarization in astronomical propylene oxide emission, we revise the (polarized) radiative transfer equation through a chiral medium in the following subsection. The production of circular polarization at the transition frequencies of a chiral molecule is the product of the simultaneous interaction of the electromagnetic radiation with the molecular electric dipole and magnetic dipole moments. In Sect. 2.2, we review the theory of the electric dipole and magnetic dipole moment of torsionally active molecules.
2.1 Radiative transfer and circular dichroism
The transfer of electromagnetic radiation through a medium with chiral molecules is characterized by the production of circular polarization at the transition frequencies of the chiral molecule, called circular dichroism, and the rotation of linear polarization away from the transition frequencies, called optical rotation. These two effects are the products of the simultaneous interaction of the electromagnetic radiation with the molecular electric dipole and magnetic dipole moments, and are related to each other through the Kramers–Kronig relations. Circular dichroism of microwave transitions is the preferred method of astronomical chirality detection as this effect occurs at the transition frequencies specific to the (chiral) molecule, and it does not require a linearly polarized background radiation field.
In Appendix A, we derive the polarized radiative transfer equation for a chiral molecule. There are other thorough derivations of interaction of radiation with chiral molecules (see, e.g., Polavarapu 2018), but here we present the polarized radiative transfer in a formalism that will be more familiar to astrophysicists. We favor this formalism as it is more suitable to astrophysical conditions, where both the emission and absorption properties of the medium need to be incorporated in the radiative transfer equation.
We consider a transition between lower state, which we denote by its angular momentum, j1, and upper state, j2. The dichroic properties of the transition have their origin in the simultaneous interaction of the electric dipole and magnetic dipole moment with the electromagnetic (EM) field. The relative interaction rate of that interaction, compared to the regular electric dipole interaction rate, is (in SI or CGS units)
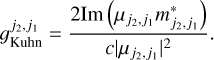 (1)
(1)
The relative interaction rate is dimensionless and is called the Kuhn dissymmetry factor. The Kuhn dissymmetry factor is dependent on the transition electric and magnetic dipole moments, 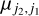 and
and 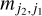 , and is normalized by the speed of light, c. In the method section and in Appendix B, we describe how the transition electric and magnetic dipole moments may be computed for a torsion–rotation transition. The equation describing the transfer of (polarized) radiation for a chiral molecule, over the optical depth τv, is derived in Appendix A, and reads
, and is normalized by the speed of light, c. In the method section and in Appendix B, we describe how the transition electric and magnetic dipole moments may be computed for a torsion–rotation transition. The equation describing the transfer of (polarized) radiation for a chiral molecule, over the optical depth τv, is derived in Appendix A, and reads
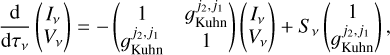 (2)
(2)
where Iv and Vv are respectively the Stokes parameters at frequency v, which represent the total (unpolarized) specific intensity, and the circular polarization. In Eq. (2), Sv is the source function given in Eq. (A.6).
A transition is circularly dichroic if Kuhn’s dissymmetry factor, 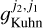 , is nonzero. From its definition, we readily observe that it is only nonzero for molecules that are chiral; the electric dipole and magnetic dipole moment operators are respectively antisymmetric and symmetric under an inversion operation, so Kuhn’s dissymmetry factor is opposite for two enantiomers and cancels out for a nonchiral molecule or a racemic mixture. From the radiative transfer equation, we note that the fractional circular polarization of an optically thin transition approaches its dissymmetry factor in the case of a homochiral sample. For an absorption line, the fractional circular polarization approaches Kuhn’s dissymmetry factor times the optical depth.
, is nonzero. From its definition, we readily observe that it is only nonzero for molecules that are chiral; the electric dipole and magnetic dipole moment operators are respectively antisymmetric and symmetric under an inversion operation, so Kuhn’s dissymmetry factor is opposite for two enantiomers and cancels out for a nonchiral molecule or a racemic mixture. From the radiative transfer equation, we note that the fractional circular polarization of an optically thin transition approaches its dissymmetry factor in the case of a homochiral sample. For an absorption line, the fractional circular polarization approaches Kuhn’s dissymmetry factor times the optical depth.
2.2 Electric and magnetic properties of propylene oxide
The properties relevant to the circular dichroism of a chiral molecule are the electric dipole and magnetic dipole moments. The electric dipole moment results from the separation of positive and negative charges in the molecule. The magnetic dipole moment of a closed-shell molecule such as propylene oxide is the result of the differential motion of its charged particles. The electric dipole moment of a molecule may be derived with relative ease from the line strengths of its transitions (Townes & Schawlow 1955). The magnetic dipole moment, on the other hand, is dependent on the motion of the nuclei and electrons, and its evaluation involves rigorous modeling of the often cumbersome rotational dynamics of that molecule. In this paper we are interested in propylene oxide, which is a torsionally active molecule, exhibiting internal rotational motion.
The full derivation of the magnetic dipole moment of torsionally active molecules was first presented by Huttner & Flygare (1969) for a molecule with its principal a-axis along the torsional-axis. Later, Sutter & Guarnieri (1970) generalized this to a molecule with an arbitrary torsional-axis. The magnetic dipole moment of a torsionally active molecule can be characterized by the rotational g-tensor, g, and the torsional b-vector, b, which are dimensionless tensors that relate the molecular (internal) rotation to its magnetic dipole moment through (Sutter & Guarnieri 1970; Lankhaar et al. 2018)
![$ {\bf{\hat m}} = - {{{\mu _N}} \over \hbar }{\bf{g\hat J}} - f{{{\mu _N}} \over \hbar }\left[ {{\bf{b}} - {\bf{g\lambda }}} \right]\left( {{{\hat p}_\gamma } - {\bf{\rho }} \cdot {\bf{\hat J}}} \right), $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq6.png) (3)
(3)
where 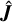 and
and 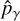 are the rotational and torsional angular momentum operators, μN and ℏ are the nuclear magneton and the reduced Planck constant, f is a dimensionless factor that depends on the ratio of the moments of inertia of the rotating top and frame, λ is the unit vector in the direction of the internal rotation, and ρ is a vector dependent on the relative inertia of the internal rotation group and the molecule.
are the rotational and torsional angular momentum operators, μN and ℏ are the nuclear magneton and the reduced Planck constant, f is a dimensionless factor that depends on the ratio of the moments of inertia of the rotating top and frame, λ is the unit vector in the direction of the internal rotation, and ρ is a vector dependent on the relative inertia of the internal rotation group and the molecule.
The magnetic dipole moment of a torsion–rotation level can be evaluated from the rotational g-tensor and torsional b-vector. While the rotational g-tensor can be accurately determined through quantum chemical modeling (Flygare & Benson 1971; Sauer 2011), no such methods exist to numerically compute the torsional b-vector. There have been some experimental efforts to measure the torsional b-vector of molecules exhibiting internal rotation. Engelbrecht et al. (1973) determined the torsional b-vectors of some simple molecules exhibiting internal rotation. Recently, Takagi et al. (2021) measured the torsional b-vector of methanol, a torsionally active molecule whose Zeeman effect can be detected in its strong maser lines (Lankhaar et al. 2018; Vlemmings 2008).
Evaluating the magnetic dipole moment of a torsion–rotation level or transition requires evaluating Eq. (3) in a torsion–rotation basis using angular momentum algebraic techniques. The proper theory of evaluating torsion–rotation level specific magnetic dipole moments from the rotational g-tensor and torsional b-vector is presented in Lankhaar et al. (2018). In Appendix B we expand on Lankhaar et al. (2018), and derive the expressions of magnetic dipole and electric dipole moment matrix elements that are general to torsion–rotation transitions. We furthermore dedicate particular attention to the antisymmetric part of the rotational g-tensor, because of the sensitivity of Kuhn’s dissymmetry parameter to it. To model the antisymmetric part of the rotational g-tensor, we follow the early work of Eshbach & Strandberg (1952), who pointed out the need to symmetrize the coupling of the magnetic field to the rotational angular momentum.
3 Methods
In the following, we present the methods that we used to compute the dichroic activity properties of propylene oxide. First, we discuss the modeling of the torsion–rotation structure of propylene oxide. After that, we discuss the electronic structure methods that we used to obtain the magnetic coupling tensors. In Appendix B, we present the proper angular momentum algebra to find their matrix elements in the basis that we used to obtain the torsion–rotation structure.
3.1 Torsion-rotation structure of propylene oxide
Propylene oxide is an asymmetric rotor molecule that is torsionally active about its C–CH3 bond, where the internal rotation is hindered by a three-fold barrier of 947.8 cm−1 (Swalen & Herschbach 1957). The internal rotation of the methyl group is associated with a potential with three equivalent minima, resulting in the splitting of each rotational state in two degenerate torsion–rotation states of E-symmetry, and one torsion–rotation state of A-symmetry. Spectroscopic studies of the microwave spectrum have been performed in the torsional ground state (Swalen & Herschbach 1957; Mesko et al. 2017) and in the excited torsional state (Stahl et al. 2021). The Hamiltonian that we used to model the torsionally active propylene oxide is described in Swalen & Herschbach (1957). We obtained torsion–rotation eigenstates through a modified internal axis method (Woods 1966; Vacherand et al. 1986; Hartwig & Dreizler 1996), where the rotational part of the Hamiltonian is set up in the principal axis system, where the inertia tensor is diagonal, while the internal rotation Hamiltonian is set up in the rho-axis system (Hougen et al. 1994) and rotated to be later incorporated into the total Hamiltonian. We used the fitting constants of Mesko et al. (2017) to set up the torsion–rotation Hamiltonian of propylene oxide. The eigenfunctions of the torsion–rotation Hamiltonian were expanded in a basis of |J(K)M〉 |υτ(K)σ〉 functions. The functions |J(K)M〉 are the regular symmetric top wave functions, with angular momentum J and body-fixed and space-fixed projection quantum numbers, K and M. These functions are expanded with the torsional functions |υτ(K)σ〉, which are determined for each K, and have the torsional quantum number υτ and symmetry quantum number σ. The torsional functions are a linear combination of ei(3q+σ)γ functions, where σ = 0 corresponds to A-symmetry states and σ = ±1 to the (degenerate) E-symmetry states, and q is an integer and truncated at |qmax|, which we chose to be 10.
3.2 Electric and magnetic properties of propylene oxide
The rotational g-tensor was obtained from ab initio electronic structure calculations with the program package CFOUR (Stanton et al. 2009). Calculations with CFOUR were carried out at the coupled-cluster level of theory including single and double excitation with perturbative treatment of the triples contributions [CCSD(T)], on a correlation-consistent polarized triple-zeta (cc-pVTZ) basis set. The rotational g-tensor was calculated for ten torsional angles γ. We fitted the torsionally dependent rotational g-tensor elements to sinusoidal functions,
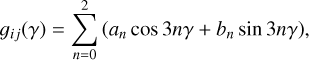 (4)
(4)
where γ = 0 corresponds to the eclipsed configuration. We obtained excellent fits of the ab initio data to the expansion functions. In Table 1 we report the fitting parameters. For most elements the variation with the torsion angle is around 10–20% of the torsionally averaged rotational g-tensor, while for the gaa and gac elements the γ-variation is larger than the average value. The calculation of the torsional b-vector has not been implemented in available quantum chemical program packages. The torsional b-vector was estimated following a procedure similar to that used in Lankhaar et al. (2018) for the similar molecule methanol. The torsional b-vector was assumed, b = gγλ, to lie along the internal rotation axis, λ. The factor gγ was put at 0.34, close to the g-factor of a general methyl group. The λ = (λa, λb, λc) = (0.8843, 0.0104, 0.4668) vector was taken from Mesko et al. (2017). For the electric dipole moment, we used the experimentally determined electric dipole moment vector (μa, μb, μc) = (0.95, 1.67, 0.56) D (Swalen & Herschbach 1957; Mesko et al. 2017). The ρ-vector and f-factor that are relevant to the magnetic interactions and energy spectrum are from Mesko et al. (2017) and are ρ = (ρa, ρb, ρb) = (0.1007, 0.0030, 0.0173) and f = 1.0997.
The values for the electric dipole moment, rotational g-tensor, and torsional b-vector were used in conjunction with the model on the torsion–rotation structure of propylene oxide to compute the magnetic and electric dipole moments of the torsion–rotation transitions of propylene oxide. We used Eq. (B.3) to compute the reduced electric dipole moment of a torsion–rotation transition, while Eqs. (B.10) were used to compute the reduced magnetic dipole moments. The dichroic properties of the torsion–rotation transitions were subsequently characterized by computing their dissymmetry factors using Eq. (1).
Circular dichroism properties of the propylene oxide microwave transitions, as observed by McGuire et al. (2016).
4 Results
McGuire et al. (2016) observed three torsion–rotation transitions of propylene oxide towards Sgr. B2(N) using the Green Bank Telescope. Through chemical and radiative transfer modeling, Das et al. (2019) identified other potentially observable transitions in ALMA bands 3 and 4. Recently, coefficients for the detailed excitation modeling of ISM propylene oxide have been presented (Dzenis et al. 2022). Tables 2 and 3 give an overview of the line properties and circular dichroism characteristics of the observed microwave transitions and the predicted ALMA band 3 and 4 transitions, respectively. All the investigated transitions are in the torsional ground state. Even though the A- and E-species of a particular transition are slightly displaced in frequency, we do not report these as individual lines, as the displacement is smaller than typical turbulent broadening in the ISM. We therefore denote transitions by their total rotational angular momentum, J, and the projection on the principal axes, Ka and Kc: 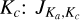 . Kuhn’s dissymmetry factors for symmetry types A and E are almost identical in all the investigated transitions. This is a result of the high barrier to the internal rotation. We therefore report a single dissymmetry factor per transition.
. Kuhn’s dissymmetry factors for symmetry types A and E are almost identical in all the investigated transitions. This is a result of the high barrier to the internal rotation. We therefore report a single dissymmetry factor per transition.
The circular dichroism properties are fully contained in Kuhn’s dissymmetry factor of the transition. An order of magnitude estimate puts the dissymmetry factor on the order of ~10−5. Most of the torsion–rotation transitions of propylene oxide have Kuhn’s dissymmetry factors that are an order of magnitude smaller than this estimate, due to the large electric dipole moment of propylene oxide and its relatively small rotational g-tensor.
Dissymmetry factors on the order of 10−6 do not produce astronomically detectable circular polarization. Only those transitions with electric dipole moments that are more than three orders of magnitude lower compared to strong transitions, transitions that are almost forbidden, show high dissymmetry factors. In Table 4, we list a range of such lines. A Kuhn dissymmetry factor of ~1 is predicted for these lines, and the emission of an enantiopure compound through these transitions is expected to be completely circularly polarized. However, due to their low transition probabilities, several orders of magnitude lower than regular transition lines, forbidden lines are extremely weak and accordingly undetectable in astrophysical regions.
Because of the minor energy difference between the two torsional symmetry states and the relatively high internal rotation barrier of propylene oxide, we investigated the relative contribution of the internal rotation on the total magnetic dipole moment. We find that the magnitude of the magnetic dipole moment that is due to the torsional motion and the coupling between the torsional and rotational motion, is about half of the total magnetic dipole moment. Even though the internal rotation barrier is high, and the difference between the two symmetry states is limited, the contribution of the molecular torsional motion to the magnetic dipole moment is still significant and should therefore be modeled rigorously.
5 Discussion
We investigated the possibility of detecting enantiomeric excess through the measurement of circular dichroism in ISM propylene oxide. Propylene oxide in the ISM is observed in its microwave transitions, which are between torsion–rotation states. To date, no experiments have been performed to measure and characterize circular dichroism in microwave transitions. Therefore, we characterized the circular dichroism of the microwave transitions of propylene oxide through theoretical means. This entailed developing the proper theory behind the circular dichroism properties of torsion–rotation transitions, which had not been established before. In the following we discuss the implications of our results for the possibility of detecting chiral asymmetry in propylene oxide by means of astronomical circular dichroism measurements and laboratory circular dichroism measurements. Thereafter, we put the developments of the theory behind circular dichroism properties of microwave transitions presented in this paper in the context of previous works.
We characterized the circular dichroism properties of the torsion–rotation transitions, using quantum-chemical techniques to determine the magnetic properties, in conjunction with accurate modeling of the torsion–rotation structure of propylene oxide. This method has been shown to be highly accurate when modeling the molecular rotational Zeeman effect (Flygare & Benson 1971; Sauer 2011), which is a property that is related to circular dichroism. The torsional contribution to the magnetic dipole moment (and circular dichroism) cannot be computed using available quantum-chemical techniques, but rather was estimated to be close to the magnetic dipole moment of a general torsionally active methyl group. Engelbrecht et al. (1973) measured the torsional magnetic dipole moments due to the internally rotating CH3 groups of nitromethane and methylboron-difluoride, and found them to be close (within 5%) to the magnetic dipole moment of methane. Recent work of Takagi et al. (2021) shows that for methanol, the torsional magnetic dipole moment associated with its CH3-group is two-thirds of the magnetic dipole moment of methane. Considering this error margin, and the relative contribution of the torsion to the total magnetic dipole moment, we conservatively predict an error of 10–15% on our estimates of the circular dichroism properties of the microwave transitions of propylene oxide. We estimate that ISM propylene oxide exhibiting an enantiomeric excess would produce circular polarization fractions in its torsion–rotation transitions on the order of 10−6–10−8. We find that the circular dichroism of propylene oxide is too weak for it to be astronomically detectable. With current sensitivity limits on circular polarization fractions of ~10−3, no currently existing astronomical detection technique exists that can measure such low levels of circular polarization.
Even if astronomical polarization instruments were available that could detect circular polarization fractions on the order of 10−6, the contamination of the circular polarization by the nonparamagnetic Zeeman effect due to the ISM magnetic field would be significant. The circular polarization produced through the Zeeman effect for a nonparamagnetic molecule such as propylene oxide, at submillimeter frequencies, with a line width and magnetic field typical of the ISM, is
![${\left[ {{p_V}} \right]_{{\rm{Zeeman}}}} \simeq 3.3 \times {10^{ - 6}}\bar g{\left( {{{\Delta {\upsilon _{{\rm{FWHM}}}}} \over {1\,{\rm{km}}\,{{\rm{s}}^{ - 1}}}}} \right)^{ - 1}}{\left( {{{{v_0}} \over {10{\rm{GHz}}}}} \right)^{ - 1}}\left( {{B \over {100\,{\rm{\mu G}}}}} \right),$](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq11.png)
where 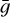 is the transition g-factor. It should be mentioned here that the circular polarization signal from the Zeeman effect is expected to exhibit an S -shaped profile, being oppositely polarized in the red and blue part of the line, while the circular polarization due to dichroism is expected to yield an even profile that follows the regular line profile.
is the transition g-factor. It should be mentioned here that the circular polarization signal from the Zeeman effect is expected to exhibit an S -shaped profile, being oppositely polarized in the red and blue part of the line, while the circular polarization due to dichroism is expected to yield an even profile that follows the regular line profile.
Characterizing the enantiomeric composition of the gasphase ISM may be achieved if a chiral radical species were found. Endowed with a paramagnetic magnetic dipole moment, radicals are significantly more dichroic, with dissymmetry factors on the order of ~10−2. Such dissymmetry factors lead to circularly polarized emission lines of a few percent for mixtures with an enantiomeric excess.
Detecting and characterizing the enantiomeric composition of a compound through circular dichroism measurements is a proven method in laboratory environments. However, such laboratory experiments have only been established for optical and vibrational transitions. Successful experiments to characterize circular dichroism in the (torsion-)rotational transitions, which occur in the microwave region of the EM spectrum, chiral molecules have not been reported yet. Laboratory experiments should be able to detect the circular polarization fractions on the order of 10−6, which we predict for some torsion–rotation transitions of propylene oxide. Additionally, any contribution of the Zeeman effect to the circular polarization of spectral lines may be mitigated by experimentally compensating for the Earth’s magnetic field. However, in order to detect and characterize chiral asymmetry through microwave lines, laboratory experiments may perhaps defer to the measurement of optical rotation, which is related to the circular dichroism by a Kramers– Kronig transformation. Significant optical rotation on the order of a radian may be achieved at optical depths of 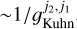 , which should be realizable in laboratory experiments. Alternatively, if an experiment is set up where the microwave transition lines are detected in significant absorption, with optical depths ≫1, this will enhance the polarization fraction to
, which should be realizable in laboratory experiments. Alternatively, if an experiment is set up where the microwave transition lines are detected in significant absorption, with optical depths ≫1, this will enhance the polarization fraction to 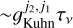 .
.
It has been suggested that nonracemic chiral mixtures may give rise to detectable circular polarization in their microwave transitions (Salzman & Polavarapu 1991; Salzman 1997). Through theoretical efforts similar in spirit to those described in this paper for microwave transitions of nontorsionally active molecules, Salzman & Polavarapu (1991) predicted dissymmetry factors that are of the same order of magnitude as the dissymmetry factors that we predict for propylene oxide. We expanded on their theory in that (i) we consider the contribution of the torsional magnetic dipole moment, and (ii) we rigorously implemented the proper symmetrization of the antisymmetric contribution to the magnetic dipole moment. Even though the internal rotation of propylene oxide is hindered by a high barrier, we find that the effect of the torsional motion on the magnetic properties is significant, contributing close to half of the total magnetic dipole moment. We therefore strongly suggest rigorously modeling the torsion–rotation dynamics and its contribution to the magnetic dipole and electric dipole moments when characterizing the circular dichroism properties of (high barrier) hindered internal rotor molecules.
Recently, there have been major advances in the detection of chiral asymmetry in compounds via microwave spectroscopy (Patterson et al. 2013; Patterson & Doyle 2013). Through a three-wave mixing scheme, where the EM waves are resonant with a-, b-, and c-type transitions (Townes & Schawlow 1955), a signal may be generated that is proportional to μaμbμc. For a chiral compound, the product μaμbμc is opposite for the two enantiomers, which makes this experiment sensitive to an enantiomeric excess (Patterson et al. 2013). Such innovative schemes may be manifested in laboratory experiments, where one can exert control over the phase of an EM wave, but have little utility in astrophysical situations.
Circular dichroism properties of the propylene oxide (sub)millimeter transitions in ALMA bands 3 and 4 as reported in Das et al. (2019).
Circular dichroism properties of some forbidden lines of propylene oxide (sub)millimeter transitions.
6 Conclusions
The expressions for the dichroic activity of torsionally active molecules were derived. Theoretical expressions for the Kuhn dissymmetry factor of microwave transitions had been derived previously (Salzman & Polavarapu 1991), but we expanded on these earlier modeling efforts by (i) extending the optical activity due to the magnetic dipole moment with the contribution of the torsional motion and (ii) performing the proper symmetrization of the interaction with the magnetic field, as prescribed by Eshbach & Strandberg (1952). We used the newly derived expressions, in combination with ab initio modeling of the relevant coupling parameters, to characterize the optical activity of the torsion–rotation transitions of propylene oxide. The results of our calculations are presented for observed and predicted propylene oxide transitions in Tables 2–4.
With the results of Tables 2–4, we predict the fractional circular polarization of a torsion–rotation line due to an enantiomeric imbalance of propylene oxide. We find that for the range of propylene oxide lines that have been predicted and observed, the predicted circular polarization fraction is on the order of 10−6−10−8. Observing such polarization fractions is beyond the current capabilities of modern telescopes. Additionally, circular polarization produced by the Zeeman effect is expected to be of similar magnitude under ISM conditions. Even so, the two effects can be disentangled due to their different spectral manifestations. While the circular polarization profile due to circular dichroism is expected to follow the line shape, the Zeeman circular polarization is expected to have an S -shaped profile. Forbidden lines may show significant polarization fractions, but the astronomical observation of forbidden transitions in low-abundance species such as propylene oxide is not feasible. Detection of enantiomeric excess in the gas-phase ISM with currently available observation techniques can only be achieved using a chiral radical species.
Laboratory measurements of circular dichroism in vibrational transitions are able to reach the sensitivity required to detect circular dichroism in microwave transitions (Polavarapu 2018). In principle, experiments to directly measure the circular dichroism of microwave transitions should be feasible. These experiments would be complementary to other detection techniques of chiral asymmetry via microwave spectroscopy (Patterson et al. 2013; Patterson & Doyle 2013). The theory presented in this paper provides a solid theoretical underpinning for circular dichroism measurements in microwave transitions.
Acknowledgements
Support for this work was provided by the Swedish Research Council (VR) under grant number 2021-00339. Simulations were performed on resources at the Chalmers Centre for Computational Science and Engineering (C3SE) provided by the Swedish National Infrastructure for Computing (SNIC). Gerrit C. Groenenboom and Ad van der Avoird are acknowledged for helpful comments on a first draft of the manuscript.
Appendix A Radiative transfer and circular dichroism
In the following we derive the circularly dichroic radiative transfer equation of chiral molecular spectral lines. In contrast to similar derivations of circular dichroic activity of electronic and vibrational transitions (Polavarapu 2018), we work in a formalism that will be more familiar to astronomers. We favor this formalism as both the emission and absorption properties of the medium are incorporated in the radiative transfer equation. We consider the interaction of an EM wave, composed of an electric field, E, and a magnetic field, B, with a molecule that possesses an electric and magnetic dipole moment, μ and m. Because the interaction of the EM wave with the electric dipole moment is much stronger than with the magnetic dipole moment, the latter interaction is often ignored. However, without the magnetic field component, light is not chiral, and circular dichroism does not emerge as a feature of the radiation transfer. Therefore, in this work, we will not make that simplification. We note the interaction Hamiltonian of a molecule interacting with an external EM field, in the dipole approximation (Loudon 2000)
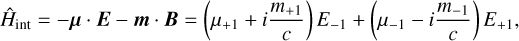 (A.1)
(A.1)
where we use the relation between the electric and magnetic field components of an EM wave as 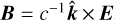 , where
, where 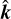 is the unit vector in the wave propagation direction and c is the speed of light, and where we use CGS units. We give the components of the electric field and molecular properties in a spherical basis
is the unit vector in the wave propagation direction and c is the speed of light, and where we use CGS units. We give the components of the electric field and molecular properties in a spherical basis 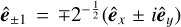 and ê0 = êz. The unit vector êz is chosen along the wave propagation direction, while êx and êy are perpendicular to each other and to ê0. For the purpose of this elementary derivation, we consider a monochromatic EM wave at (natural) frequency ω that is traveling along the
and ê0 = êz. The unit vector êz is chosen along the wave propagation direction, while êx and êy are perpendicular to each other and to ê0. For the purpose of this elementary derivation, we consider a monochromatic EM wave at (natural) frequency ω that is traveling along the 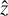 -direction, so that its electric field components are E±1 = Re[ℰ±1e−iω(t−z/c)], where ℰ±1 are the complex amplitudes.
-direction, so that its electric field components are E±1 = Re[ℰ±1e−iω(t−z/c)], where ℰ±1 are the complex amplitudes.
We consider a transition between two states that are separated in energy by ℏω0, and that have angular momentum, j1 and j2. For our purposes it is important to pay more attention to the degeneracy of the rotational levels. A level j is split up into [j] = 2j + 1 sublevels denoted by the magnetic quantum number m: |jm〉. So, to resolve the degeneracy of the transition states, we consider the transitions |j1m1〉 ↔|j2m2〉, over which we will later average. The interaction between the EM wave and the molecule gives rise to a transition between j1 and j2 when the EM wave frequency, ω, approaches ω0. Fermi’s golden rule puts the transition rate at (Merzbacher 1961)
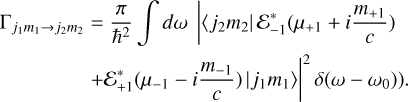 (A.2)
(A.2)
In order to obtain matrix elements of the electric dipole and magnetic dipole moments, we use the Wigner–Eckart theorem (Biedenharn et al. 1981; Blum 1981),
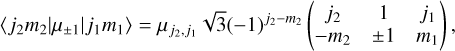 (A.3a)
(A.3a)
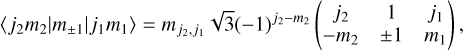 (A.3b)
(A.3b)
where the entity in brackets is the Wigner 3 j symbol, and 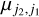 and
and 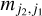 are the reduced matrix elements of the electric and magnetic dipole moments. In Appendix B, we derive detailed expressions to quantify the reduced matrix elements for a particular torsion–rotation transition. The rate of absorption from the level |j1m1〉 to all possible levels in j2, is
are the reduced matrix elements of the electric and magnetic dipole moments. In Appendix B, we derive detailed expressions to quantify the reduced matrix elements for a particular torsion–rotation transition. The rate of absorption from the level |j1m1〉 to all possible levels in j2, is
![$ \matrix{ {{\Gamma _{{j_1}{m_1} \to {j_2}}}} \hfill & = \hfill & {\sum\limits_{{m_2}} {{\Gamma _{\left| {\left. {{j_1}{m_1}} \right\rangle } \right. \to \left. {\left| {{j_2}{m_2}} \right.} \right\rangle }}} } \hfill \cr {} \hfill & = \hfill & {{\pi \over {3\left[ {{j_1}} \right]{\hbar ^2}}}\left\{ {\left[ {{{\left| {{\mu _{{j_2},{j_1}}}} \right|}^2} + {{\left| {{{{m_{{j_2},{j_1}}}} \over c}} \right|}^2}} \right]\left( {{{\left| {{{\cal E}_{ + 1}}\left( v \right)} \right|}^2} + {{\left| {{{\cal E}_{ - 1}}\left( v \right)} \right|}^2}} \right)} \right.} \hfill \cr {} \hfill & + \hfill & {2{\rm{Im}}\left( {{{{\mu _{{j_2},{j_1}}}m_{{j_2},{j_1}}^*} \over c}} \right)\left. {\left[ {{{\left| {{{\cal E}_{ + 1}}\left( v \right)} \right|}^2} - {{\left| {{{\cal E}_{ - 1}}\left( v \right)} \right|}^2}} \right]} \right\}} \hfill \cr {} \hfill & = \hfill & {{B_{{j_1} \to {j_2}}}\left( {\left[ {1 + R_{{\rm{m}}.{\rm{d}}{\rm{.}}}^{{j_2},{j_1}}} \right]{I_v} + g_{{\rm{Kuhn}}}^{{j_2},{j_{\rm{l}}}}{V_v}} \right),} \hfill \cr } $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq25.png) (A.4a)
(A.4a)
where 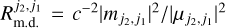 is the ratio of the magnetic to the electric dipole moment transition strength, and
is the ratio of the magnetic to the electric dipole moment transition strength, and 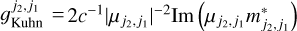 is the Kuhn dissymmetry factor. The Stokes parameters are related to the electric field amplitudes as Iv = c/8π(|ℰ+1 (v)|2 + |ℰ−1 (v)|2) and Vv = c/8π(|ℰ+1 (v)|2 − |ℰ−1 (v)|2) and are given for frequency v = ω0/2π. The Einstein B coefficient is defined as
is the Kuhn dissymmetry factor. The Stokes parameters are related to the electric field amplitudes as Iv = c/8π(|ℰ+1 (v)|2 + |ℰ−1 (v)|2) and Vv = c/8π(|ℰ+1 (v)|2 − |ℰ−1 (v)|2) and are given for frequency v = ω0/2π. The Einstein B coefficient is defined as ![${B_{{j_1} \to {j_2}}} = {{8{\pi ^2}} \over {3\left[ {{j_1}} \right]{\hbar ^2}c}}{\left| {{\mu _{{j_2},{j_1}}}} \right|^2}$](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq28.png) . Similar to the rate of absorption, the rate of stimulated emission events can be derived to be
. Similar to the rate of absorption, the rate of stimulated emission events can be derived to be
![$ {\Gamma _{{j_2}{m_2} \to {j_1}}} = {B_{{j_2} \to {j_1}}}\left( {\left[ {1 + R_{{\rm{m}}.{\rm{d}}{\rm{.}}}^{{j_1},{j_2}}} \right]} \right.\left. {{I_v} + g_{{\rm{Kuhn}}}^{{j_1},{j_2}}{V_v}} \right), $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq29.png) (A.4b)
(A.4b)
where it should be noted that 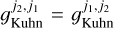 . The rate of spontaneous emission bears a close relation to the rate of stimulated emission.
. The rate of spontaneous emission bears a close relation to the rate of stimulated emission.
The interactions of the radiation field with the chiral molecule, whose rates are given in Eqs. (A.4), will manifest in the transfer of polarized radiation. It can be noted from Eqs. (A.4) that the absorption of Stokes V radiation occurs at a rate of 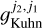 times the absorption of Stokes I radiation. Similarly, the production of Stokes V radiation occurs at a rate of
times the absorption of Stokes I radiation. Similarly, the production of Stokes V radiation occurs at a rate of 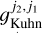 times the production of Stokes I radiation through stimulated and spontaneous emission processes. More specifically, the change in flux density, per optical depth, may be noted
times the production of Stokes I radiation through stimulated and spontaneous emission processes. More specifically, the change in flux density, per optical depth, may be noted
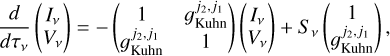 (A.5)
(A.5)
where dτv = κvds is the optical depth over an infinitesimal distance ds, and
![${K_v} = {{hv} \over {4\pi }}{B_{{j_1} \to {j_2}}}\left( {{n_{{j_1}}} - {{\left[ {{j_1}} \right]} \over {\left[ {{j_2}} \right]}}{n_{{j_2}}}} \right){\phi _v}$](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq34.png)
is the absorption coefficient (Rybicki & Lightman 2008), dependent on the number densities, nj, of levels j1 and j2 and the line profile ϕv. The quantity Sv is the source function, which is defined by the ratio of the emission to the absorption coefficient (Rybicki & Lightman 2008),
![$ {S_v} = {{2h{v^3}} \over {{c^2}}}{\left[ {{{\left[ {{j_2}} \right]{n_1}} \over {\left[ {{j_1}} \right]{n_2}}} - 1} \right]^{ - 1}}, $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq35.png) (A.6)
(A.6)
which approaches Planck’s function for a thermalized transition.
Appendix B Electric and magnetic dipole moments of torsion–rotation transitions
The electric dipole moment results from the separation of positive and negative charges in the molecule and may be computed as μ = ∑jqjrj, where qj is the charge of particle j and rj is its position. The magnetic dipole moment of a closed-shell molecule such as propylene oxide is the result of the differential motion of its charged particles. The classical definition of the magnetic dipole moment of a set of moving charged particles is (Jackson 1998)
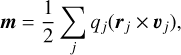 (B.1)
(B.1)
where vj is the velocity of particle j. For a molecule such as propylene oxide, the motion of the nucleus is determined by its rotational motion, and by the internal rotational motion. Lankhaar et al. (2018) derived the magnetic dipole moment of a torsionally active molecule. We recall here the expressions for the magnetic dipole moment (see Eqs. 1–2 of Lankhaar et al. 2018), but separate them into the terms
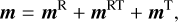 (B.2a)
(B.2a)
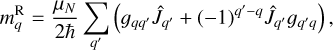 (B2b)
(B2b)
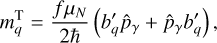 (B.2c)
(B.2c)
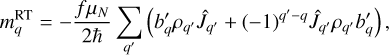 (B.2d)
(B.2d)
which are analogous to a purely rotational magnetic dipole moment, a purely torsional magnetic dipole moment, and the remaining rotation-torsion contribution. The separation into these terms will allow a clearer treatment of the angular momentum algebra lateron. We note in Eqs. (B.2) the spherical element, q, of the angular momentum operator, 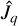 , and the torsional momentum operator,
, and the torsional momentum operator, 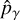 (for a definition, see Lankhaar et al. 2018). The tensors g and b are the (rank 2) rotational g-tensor and the (rank 1) torsional b-vector (Sutter & Flygare 1976; Lankhaar et al. 2018). The ρ-vector is defined in Lankhaar et al. (2018). The quantity μN is the nuclear magneton, ℏ is the reduced Planck constant, and f is a dimensionless factor that depends on the ratio of the moments of inertia of the rotating top and frame (for a definition, see Lankhaar et al. 2018; Hougen et al. 1994). We symmetrized the magnetic dipole moment interactions of Eqs. (B.2) as prescribed in Eshbach & Strandberg (1952).
(for a definition, see Lankhaar et al. 2018). The tensors g and b are the (rank 2) rotational g-tensor and the (rank 1) torsional b-vector (Sutter & Flygare 1976; Lankhaar et al. 2018). The ρ-vector is defined in Lankhaar et al. (2018). The quantity μN is the nuclear magneton, ℏ is the reduced Planck constant, and f is a dimensionless factor that depends on the ratio of the moments of inertia of the rotating top and frame (for a definition, see Lankhaar et al. 2018; Hougen et al. 1994). We symmetrized the magnetic dipole moment interactions of Eqs. (B.2) as prescribed in Eshbach & Strandberg (1952).
We derive the matrix elements of the electric dipole and magnetic dipole moment operators that are relevant to transitions between the two states, which are denoted 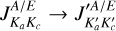 , where J is the total angular momentum, Ka and Kc are the projections of the angular momentum on the principal a and c axes, and A/E denotes the symmetry type. As discussed in section 3.1, the eigenfunctions of the torsion–rotation levels are expanded in a basis of |j(k)m〉 |υτ(k)σ〉 functions. In the following we discuss the matrix elements of the electric and magnetic dipole moment operators in these basis functions.
, where J is the total angular momentum, Ka and Kc are the projections of the angular momentum on the principal a and c axes, and A/E denotes the symmetry type. As discussed in section 3.1, the eigenfunctions of the torsion–rotation levels are expanded in a basis of |j(k)m〉 |υτ(k)σ〉 functions. In the following we discuss the matrix elements of the electric and magnetic dipole moment operators in these basis functions.
Electric dipole moment. The general matrix element of the transition electric dipole moment can be factorized,
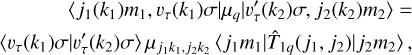 (B.3)
(B.3)
because the torsional part does not interact with the electric dipole operator as we neglected any dependence of it on the torsional angle. We use the Wigner-Eckart theorem for the rotational part, which we formulate in terms of the rank 1 irreducible spherical tensor operator 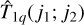 , which is defined following Blum (1981), by
, which is defined following Blum (1981), by
![$ {\hat T_{LP}}\left( {{j_1};{j_2}} \right) = \sum\limits_{{m_1}{m_2}} {\left| {\left. {{j_1}{m_1}} \right\rangle } \right.} \left. {\left\langle {{j_2}{m_2}} \right.} \right|{\left[ L \right]^{1/2}}{\left( { - 1} \right)^{{j_1} - {m_1}}}\left( {\matrix{ {{j_1}} \hfill & L \hfill & {{j_2}} \hfill \cr { - {m_1}} \hfill & P \hfill & {{m_2}} \hfill \cr } } \right), $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq46.png) (B.4)
(B.4)
where L is the rank and P its projection. We note the rotation of the electric dipole moment (rank 1 tensor) between the space-fixed (SF) laboratory frame and body-fixed (BF) principal axis frame as 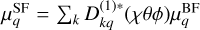 , in terms of Wigner D-matrix elements of the Euler angles χ, θ, and ϕ. We can express the Wigner D-matrix elements in terms of the irreducible tensor operators of Eq. (B.4) (see also equation (B.5) of Lankhaar et al. 2016). The irreducible matrix element is then readily derived as
, in terms of Wigner D-matrix elements of the Euler angles χ, θ, and ϕ. We can express the Wigner D-matrix elements in terms of the irreducible tensor operators of Eq. (B.4) (see also equation (B.5) of Lankhaar et al. 2016). The irreducible matrix element is then readily derived as
![$ {\mu _{{j_1}{k_1},{j_2}{k_2}}} = \sqrt {{{\left[ {{j_1}} \right]\left[ {{j_2}} \right]} \over 3}} {\left( { - 1} \right)^{{j_1} - {k_1}}}\sum\limits_k {\left( {\matrix{ {{j_1}} \hfill & 1 \hfill & {{j_2}} \hfill \cr { - {k_1}} \hfill & k \hfill & {{k_2}} \hfill \cr } } \right)} {\mu _k}, $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq48.png) (B.5)
(B.5)
where the sum over k runs over all the principal axis components (in a spherical basis) of the electric dipole tensor.
Magnetic moment. In Eq. (B.2), we formulated the magnetic dipole moment in terms of a purely rotational magnetic dipole moment, torsional magnetic dipole moment, and the residual torsion–rotation magnetic dipole moment. We begin by deriving expressions for the matrix element of the pure rotational magnetic dipole moment. We accounted for the dependance of the rotational g-tensor on the torsional angle by expanding it as  . We then factorize:
. We then factorize:
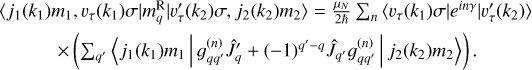 (B.6)
(B.6)
We note that a rotation of the rotational g-tensor, 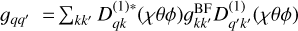 , can be decomposed into a rotation of its three irreducible elements (L = 0, 1, 2). Coupling these to the rotation operator yields
, can be decomposed into a rotation of its three irreducible elements (L = 0, 1, 2). Coupling these to the rotation operator yields
![$ \matrix{ {\left. {\left\langle {{j_1}} \right.\left( {{k_1}} \right){m_1}} \right|\sum\limits_{q'} {g_{qq'}^{\left( n \right)}} ,{{\hat J}_{q'}}\left| {{j_2}} \right.\left. {\left( {{k_2}} \right){m_2}} \right\rangle } \hfill \cr { = \sum\limits_L {g_{{j_1}{k_1},{j_2}{k_2}}^{\left( L \right),\left( n \right)}} \left. {\left\{ {{j_1}{m_1}} \right.} \right|\left[ {{{{\bf{\hat T}}}_L} \otimes {\bf{\hat J}}} \right]_q^1\left. {\left| {{j_2}{m_2}} \right.} \right\},} \hfill \cr } $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq52.png) (B.7a)
(B.7a)
![$ \matrix{ {\left. {\left\langle {{j_1}} \right.\left( {{k_1}} \right){m_1}} \right|\sum\limits_{q'} {{{\left( { - 1} \right)}^{q' - q}}} {{\hat J}_{q'}}g_{qq'}^{\left( n \right)}\left| {{j_2}} \right.\left. {\left( {{k_2}} \right){m_2}} \right\rangle } \hfill \cr { = \sum\limits_L {{{\left( { - 1} \right)}^L}g_{{j_1}{k_1},{j_2}{k_2}}^{\left( L \right),\left( n \right)}} \left. {\left\langle {{j_1}{m_1}} \right.} \right|\left[ {{\bf{\hat J}} \otimes {{{\bf{\hat T}}}_L}} \right]_q^1\left. {\left| {{j_2}{m_2}} \right.} \right\rangle ,} \hfill \cr } $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq53.png) (B.7b)
(B.7b)
where we use a short-hand notation for the product of the rotational tensors irreducible elements
![$\left[ {{{{\bf{\hat A}}}_{{L_1}}} \otimes {{{\bf{\hat B}}}_{{L_2}}}} \right]_M^L = \sum\limits_{{m_1}{m_2}} {C_{{m_1}{m_2}M}^{{L_1}{L_2}L}} {\hat A_{{L_1}{m_1}}}{\hat B_{{L_2}{m_2}}},$](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq54.png)
where 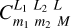 is a Clebsch-Gordan coefficient. The elements of the reduced rotational g-tensor read
is a Clebsch-Gordan coefficient. The elements of the reduced rotational g-tensor read
![$ g_{{j_1}{k_1},{j_2}{k_2}}^{\left( L \right),\left( n \right)} = {\left( { - 1} \right)^L}\sqrt {{{\left[ {{j_1}} \right]\left[ {{j_2}} \right]} \over {\left[ L \right]}}} {\left( { - 1} \right)^{{j_1} - {k_1}}}\sum\limits_Q {\left( {\matrix{ {{j_1}} \hfill & L \hfill & {{j_2}} \hfill \cr { - {k_1}} \hfill & Q \hfill & {{k_2}} \hfill \cr } } \right)} g_{LQ}^{\left( n \right)}, $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq56.png) (B.8)
(B.8)
where  are the irreducible tensor elements of the rotational g-tensor in the body-fixed frame. As expected, the sum of both parts of mR cancel each other out at uneven (antisymmetric) L. However, it should be noted that the angular momentum operators,
are the irreducible tensor elements of the rotational g-tensor in the body-fixed frame. As expected, the sum of both parts of mR cancel each other out at uneven (antisymmetric) L. However, it should be noted that the angular momentum operators, 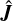 and
and 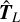 , do not commute for L = 1. We note the commutation relation between a tensor operator and the spherical components of the angular momentum operator (see Eq. (3.210) of Biedenharn et al. 1981),
, do not commute for L = 1. We note the commutation relation between a tensor operator and the spherical components of the angular momentum operator (see Eq. (3.210) of Biedenharn et al. 1981), ![$\left[ {{{\hat J}_m},{{\hat T}_{JM}}} \right] = \sqrt {J\left( {J + 1} \right)} C_{M\,\,m\,\,M + m}^{J\,\,1\,\,J}\,{{\hat T}_{J,M + m}}$](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq60.png) , from which we derive
, from which we derive
![$\left[ {{{{\bf{\hat T}}}_L} \otimes {\bf{\hat J}}} \right]_q^1 - \left[ {{\bf{\hat J}} \otimes {{{\bf{\hat T}}}_L}} \right]_q^1 = - \sqrt 2 {\hat T_{1q}}{\delta _{L,1}}.$](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq61.png)
Using angular momentum algebra we can couple the product
![$ \matrix{ {\left. {\left\langle {{j_1}} \right.{m_1}} \right|\left. {\left[ {{{{\bf{\hat T}}}_L} \otimes {\bf{\hat J}}} \right]_q^1} \right|\left. {{j_2}{m_2}} \right\rangle } \hfill & = \hfill & {{{\left( { - 1} \right)}^{1 + {j_1} + {j_2}}}\sqrt {\left[ {{j_2}} \right]\left[ L \right]{j_2}\left( {{j_2} + 1} \right)} } \hfill \cr {} \hfill & \times \hfill & {\left\{ {\matrix{ {{j_1}} \hfill & {{j_2}} \hfill & L \hfill \cr 1 \hfill & 1 \hfill & {{j_2}} \hfill \cr } } \right\}\left\langle {{j_1}{m_1}\left| {{T_{1q}}} \right|{j_2}{m_2}} \right\rangle ,} \hfill \cr } $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq62.png) (B.9)
(B.9)
where the entity between the curly brackets is a Wigner 6 j-symbol. Putting Eqs. (B.6)–(B.9) together, we derive the matrix element of the pure rotational magnetic dipole moment:
![$ \eqalign{ & \left\langle {{j_1}} \right.\left. {\left( {{k_1}} \right){m_1}} \right|\left. {m_q^{\rm{R}}} \right|{j_2}\left( {{k_2}} \right)\left. {{m_2}} \right\rangle = {{{\mu _N}} \over \hbar }\sum\limits_n {{e^{in\gamma }}} \left( {{{g_{{j_1}{k_1},{j_2}{k_2}}^{\left( 1 \right),\left( n \right)}} \over {\sqrt 2 }}} \right. + {\left( { - 1} \right)^{{j_1} + {j_2}}}\sum\limits_{L = 0,2} {} \cr & \times g_{{j_1}{k_1},{j_2}{k_2}}^{\left( L \right),\left( n \right)}\sqrt {\left[ {{j_2}} \right]\left[ L \right]{j_2}\left( {{j_2} + 1} \right)} \left. {\left\{ {\matrix{ {{j_1}} \hfill & {{j_2}} \hfill & L \hfill \cr 1 \hfill & 1 \hfill & {{j_2}} \hfill \cr } } \right\}} \right)\left. {{j_1}{m_1}} \right|\left. {{T_{1q}}} \right|\left. {{j_2}{m_2}} \right\rangle \cr} $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq63.png) (B.10a)
(B.10a)
The rotation-torsion residual contribution to the magnetic dipole moment has a similar form to the rotational magnetic dipole moment. Replacing the g-tensor elements gqq′ → bqρq′ we arrive, after performing similar angular momentum algebraic manipulations, at the expression
![$ \eqalign{ & \left\langle {{j_1}} \right.\left. {\left( {{k_1}} \right){m_1}} \right|\left. {m_q^{{\rm{RT}}}} \right|{j_2}\left( {{k_2}} \right)\left. {{m_2}} \right\rangle = {{f{\mu _N}} \over \hbar }\sum\limits_n {{e^{in\gamma }}} \left( {{{\zeta _{{j_1}{k_1},{j_2}{k_2}}^{\left( 1 \right),\left( n \right)}} \over {\sqrt 2 }}} \right. + {\left( { - 1} \right)^{{j_1} + {j_2}}}\sum\limits_{L = 0,2} {} \cr & \times \zeta _{{j_1}{k_1},{j_2}{k_2}}^{\left( L \right),\left( n \right)}\sqrt {\left[ {{j_2}} \right]\left[ L \right]{j_2}\left( {{j_2} + 1} \right)} \left. {\left\{ {\matrix{ {{j_1}} \hfill & {{j_2}} \hfill & L \hfill \cr 1 \hfill & 1 \hfill & {{j_2}} \hfill \cr } } \right\}} \right)\left. {\left\langle {{j_1}{m_1}} \right.} \right|\left. {{T_{1q}}} \right|\left. {{j_2}{m_2}} \right\rangle , \cr} $](/articles/aa/full_html/2022/10/aa44295-22/aa44295-22-eq64.png) (10b)
(10b)
where the elements 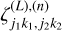 , have the same definition as Eq. (B.8), only replacing
, have the same definition as Eq. (B.8), only replacing 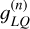 with
with 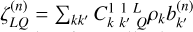 .
.
Finally, we work out the pure torsional contribution to the magnetic dipole moment. Here, the matrix element can be factorized as
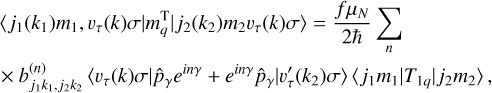 (B.10c)
(B.10c)
where the Wigner–Eckart theorem for the rotational part of the operator is of a similar form to the electric dipole operator, and the elements 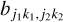 have the same definition as Eq. (B.5), replacing the electric dipole moment elements μk with the torsional b-vector elements. Expressions to evaluate the torsional elements
have the same definition as Eq. (B.5), replacing the electric dipole moment elements μk with the torsional b-vector elements. Expressions to evaluate the torsional elements 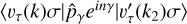 and 〈υτ(k)σ|einγ|υ′τ(k2)σ〉 can be found in Lankhaar et al. (2016).
and 〈υτ(k)σ|einγ|υ′τ(k2)σ〉 can be found in Lankhaar et al. (2016).
References
- Avnir, D. 2020, New Astron. Rev., 101596 [Google Scholar]
- Bergantini, A., Abplanalp, M. J., Pokhilko, P., et al. 2018, ApJ, 860, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Biedenharn, L. C., Louck, J. D., & Carruthers, P. A. 1981, Angular Momentum in Quantum Physics: Theory and Application (Reading, MA: Addison-Wesley) [Google Scholar]
- Bloino, J., & Barone, V. 2012, J. Chem. Phys., 136, 124108 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, K. 1981, Density Matrix Theory and Applications, Physics of Atoms and Molecules (New York: Plenum) [Google Scholar]
- Boyd, R. N., & Famiano, M. A. 2018, Creating the Molecules of Life (IOP Publishing) [Google Scholar]
- Caldwell, D. J. 1969, J. Chem. Phys., 51, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, G., Zema, N., Turchini, S., et al. 2007, J. Chem. Phys., 127, 124310 [NASA ADS] [CrossRef] [Google Scholar]
- Cronin, J. R., & Pizzarello, S. 1997, Science, 275, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Das, A., Gorai, P., & Chakrabarti, S. K. 2019, A&A, 628, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dreiling, J., & Gay, T. J. 2014, Phys. Rev. Lett., 113, 118103 [NASA ADS] [CrossRef] [Google Scholar]
- Dzenis, K., Faure, A., McGuire, B. A., et al. 2022, ApJ, 926, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbrecht, L., Sutter, D., & Dreizier, H. 1973, Z. Naturforsch. A, 28, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Eshbach, J. R., & Strandberg, M. W. P. 1952, Phys. Rev., 85, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Eyring, H., Liu, H.-C., & Caldwell, D. 1968, Chem. Rev., 68, 525 [Google Scholar]
- Flores, J. J., Bonner, W. A., & Massey, G. A. 1977, J. Am. Chem. Soc., 99, 3622 [Google Scholar]
- Flygare, W., & Benson, R. 1971, Mol. Phys., 20, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia, G. A., Dossmann, H., Nahon, L., Daly, S., & Powis, I. 2014, Phys. Chem. Chem. Phys., 16, 16214 [NASA ADS] [CrossRef] [Google Scholar]
- Gellman, A. J., Tysoe, W. T., & Zaera, F. 2015, Catal. Lett., 145, 220 [CrossRef] [Google Scholar]
- Hartwig, H., & Dreizler, H. 1996, Z. Naturforsch. A, 51, 923 [NASA ADS] [Google Scholar]
- Hilborn, R. C. 1982, Am. J. Phys., 50, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Holzwarth, G., Hsu, E. C., Mosher, H. S., Faulkner, T. R., & Moscowitz, A. 1974, J. Am. Chem. Soc., 96, 251 [CrossRef] [Google Scholar]
- Hougen, J., Kleiner, I., & Godefroid, M. 1994, J. Mol. Spectrosc., 163, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Huttner, W., & Flygare, W. H. 1969, Trans. Faraday Soc., 65, 1953 [CrossRef] [Google Scholar]
- Jackson, J. D. 1998, Classical Electrodynamics, 3rd edn. (New York: Wiley) [Google Scholar]
- Kawiecki, R. W., Devlin, F., Stephens, P., Amos, R., & Handy, N. 1988, Chem. Phys. Lett., 145, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Lankhaar, B., Groenenboom, G. C., & van der Avoird, A. 2016, J. Chem. Phys., 145, 244301 [Google Scholar]
- Lankhaar, B., Vlemmings, W., Surcis, G., et al. 2018, Nat. Astron., 2, 145 [Google Scholar]
- Loudon, R. 2000, The Quantum Theory of Light (Oxford University Press) [Google Scholar]
- McGuire, B. A., Carroll, P. B., Loomis, R. A., et al. 2016, Science, 352, 1449 [Google Scholar]
- Merzbacher, E. 1961 Quantum mechanics. (Jones & Bartlett Publishers) [Google Scholar]
- Mesko, A., Zou, L., Carroll, P. B., & Weaver, S. L. W. 2017, J. Mol. Spectr., 335, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Modica, P., Meinert, C., de Marcellus, P., et al. 2014, ApJ, 788, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, D., & Doyle, J. M. 2013, Phys. Rev. Lett., 111, 023008 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, D., Schnell, M., & Doyle, J. M. 2013, Nature, 497, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Polavarapu, P. L. 2018, Chiral Analysis: Advances in Spectroscopy, Chromatography and Emerging Methods (Elsevier) [Google Scholar]
- Polavarapu, P., Hess, B., Jr. & Schaad, L. 1985, J. Chem. Phys., 82, 1705 [NASA ADS] [CrossRef] [Google Scholar]
- Rizzo, A., & Vahtras, O. 2011, J. Chem. Phys., 134, 244109 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 2008, Radiative Processes in Astrophysics (John Wiley & Sons) [Google Scholar]
- Salzman, W. 1997, J. Chem. Phys., 107, 2175 [NASA ADS] [CrossRef] [Google Scholar]
- Salzman, W., & Polavarapu, P. 1991, Chem. Phys. Lett., 179, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sauer, S. P. 2011, Molecular Electromagnetism: A Computational Chemistry Approach (Oxford University Press) [CrossRef] [Google Scholar]
- Stahl, P., Arenas, B. E., Zingsheim, O., et al. 2021, J. Mol. Spectrosc., 378, 111445 [NASA ADS] [CrossRef] [Google Scholar]
- Stanton, J., Gauss, J.M.E.H., & Szalay, P. 2009, CFOUR, Coupled-Cluster techniques for Computational Chemistry [Google Scholar]
- Stephens, P. J. 1985, J. Phys. Chem., 89, 748 [CrossRef] [Google Scholar]
- Stranges, S., Turchini, S., Alagia, M., et al. 2005, J. Chem. Phys., 122, 244303 [NASA ADS] [CrossRef] [Google Scholar]
- Sutter, D., & Guarnieri, A. 1970, Z. Naturforsch. A, 25, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Sutter, D., & Flygare, W. 1976, in Bonding Structure. Topics in Current Chemistry, 63, eds. D. Craig, D. Mellor, R. Gleiter, et al. (Berlin, Heidelberg: Springer) 89 [Google Scholar]
- Swalen, J. D., & Herschbach, D. R. 1957, Chem. Phys., 27, 100 [NASA ADS] [Google Scholar]
- Takagi, K., Tsunekawa, S., Kobayashi, K., Hirota, T., & Matsushima, F. 2021, J. Mol. Spectrosc., 377, 111420 [NASA ADS] [CrossRef] [Google Scholar]
- Townes, C., & Schawlow, A. 1955, Microwave Spectroscopy, (McGraw-Hill Book Company) [Google Scholar]
- Turchini, S., Zema, N., Contini, G., et al. 2004, Phys. Rev. A, 70, 014502 [NASA ADS] [CrossRef] [Google Scholar]
- Ulbricht, T., & Vester, F. 1962, Tetrahedron, 18, 629 [CrossRef] [Google Scholar]
- Vacherand, J., Van Eijck, B., Burie, J., & Demaison, J. 1986, J. Mol. Spectrosc., 118, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Vlemmings, W. 2008, A&A, 484, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woods, R. C. 1966, J. Mol. Spectrosc., 21, 4 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Circular dichroism properties of the propylene oxide microwave transitions, as observed by McGuire et al. (2016).
Circular dichroism properties of the propylene oxide (sub)millimeter transitions in ALMA bands 3 and 4 as reported in Das et al. (2019).
Circular dichroism properties of some forbidden lines of propylene oxide (sub)millimeter transitions.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


