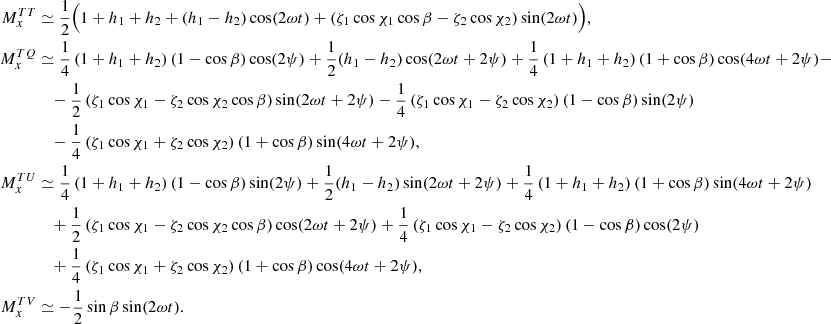| Issue |
A&A
Volume 671, March 2023
|
|
|---|---|---|
| Article Number | C1 | |
| Number of page(s) | 3 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202141619e | |
| Published online | 07 March 2023 | |
Detailed study of HWP non-idealities and their impact on future measurements of CMB polarization anisotropies from space (Corrigendum)
1
Dipartimento di Fisica e Scienze della Terra, Università di Ferrara, Polo Scientifico e Tecnologico – Edificio C Via Saragat, 1, 44122 Ferrara, Italy
e-mail: serena.giardiello@unife.it
2
Istituto Nazionale di Fisica Nucleare, sezione di Ferrara, Polo Scientifico e Tecnologico – Edificio C Via Saragat, 1, 44122 Ferrara, Italy
3
Université de Paris, CNRS, Astroparticule et Cosmologie, 75006 Paris, France
4
Istituto Nazionale di Astrofisica, Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, via Gobetti 101, 40129 Bologna, Italy
5
Istituto Nazionale di Fisica Nucleare, Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
6
Department of Physics, Okayama University, 3-1-1 Tsushimanaka, Kita-ku, Okayama 700-8530, Japan
7
Dipartimento di Fisica, Sapienza Università di Roma, sezione di Roma1, P.le A. Moro 5, 00185 Roma, Italy
8
Istituto Nazionale di Fisica Nucleare, sezione di Roma 1, P.le A. Moro 5, 00185 Roma, Italy
Key words: cosmic background radiation / instrumentation: polarimeters / cosmology: observations / techniques: polarimetric / errata, addenda
In Eq. (7) of the paper we introduce the substitution
where ω is the half-wave plate (HWP) rotation frequency and ψ is the orientation angle of the instrument boresight. This substitution is carried through all the time-ordered data (TOD) equations. However, it is strictly valid only in the case of an ideal HWP.
By computing the Mueller matrix of the full optical chain,
where ξ is the polarizer orientation in the focal plane (ξ = 0 for a polarizer at the x-axis, ξ = π/2 for a polarizer at the y-axis), we get the correct expressions of the Mueller matrix elements expanded at first order in the non ideal parameters (equivalent to Eqs. (28)–(30) in the paper):
– h1, h2 ≠ 0:
– β ≠ 0:
– ζ1, ζ2, χ1, χ2 ≠ 0:
With a non-ideal HWP with h1 ≠ h2 ≠ 0, β ≠ 0 and ζ1cosχ1 ≠ ζ2cosχ2 ≠ 0, the substitution
in
(the optical chain considered in the paper) leads to an expression of the Mueller matrix elements that is not equivalent to the correct result from Eq. (2).
Nevertheless, we expect the results in the paper not to be affected, since terms modulated at 2ωt are averaged out in the map-making procedure (see Figs. 3 and 4 in the paper). In fact, the MTT terms (obtained with the substitution in Eq. (1)) in the paper are more worrisome than the correct ones. Indeed, terms modulated as cos/sin(2ωt + ψ(t)) instead of cos/sin(2ωt + constant angle) appear in the incorrect MTT elements. As an example, if we had included the monopole in the input maps, it would have been modulated to higher frequencies.
Constant terms (i.e., independent of ωt) are supposed to be filtered out in the map-making procedure.
The amended expressions for Eqs. (A3)–(A4) in the appendix are as follows. Considering a polarimeter along the x-axis (ξ = 0):
The corresponding elements when the polarizer is along the y-axis (ξ = π/2) direction are:
We computed the residual power spectrum caused by perturbing all the HWP parameters in the TOD with a Gaussian distributed error with σ = 0.001, both with the wrong MTT/TQ/TU expressions and the corrected ones. We followed the same procedure outlined in the paper, just considering one realization of errors, which is the same for the two output maps. The residuals are computed with respect to a template map where the HWP parameters are unperturbed in both TOD and map-making (again, we have computed two template maps with the wrong and corrected expressions). The two residual power spectra are very similar, confirming the claim that the error in the Mueller matrix expressions does not significantly affect the overall result of the work.
 |
Fig. 1. Residual |
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
All Figures
 |
Fig. 1. Residual |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.