EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 642 (October 2020) A&A, 642 (2020) A130 Full HTML
Free Access
Issue
A&A
Volume 642, October 2020
Article Number A130
Number of page(s) 7
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202038830
Published online 13 October 2020

© ESO 2020

1. Introduction

Thermal equilibrium cannot be established in the outer corona and solar wind, as evidenced by the suprathermal populations of electrons, protons, and minor ions (Vasyliunas 1968; Collier et al. 1996; Maksimovic et al. 1997), for which the mean-free-path of Coulomb collisions is much longer than any scales of variation. Suprathermal particles enhance the high-energy tails of the observed distributions up to a few keV (still nonrelativistic) and are well described by the so-called κ-power laws or Kappa distribution functions; see reviews by Pierrard & Lazar (2010) and Lazar et al. (2012).

Suprathermal electrons are particularly important. Their number density may only rarely exceed 10% of the total density of electrons, but instead these electrons have kinetic energies that are much higher than (quasi)thermal electrons in the core of the observed distributions (Maksimovic et al. 2005; Štverák et al. 2008; Pierrard et al. 2016; Wilson et al. 2019a). For energies up to a few keV, two distinct suprathermal populations are observed in the solar wind: an ubiquitous electron halo, which is present even in the absence of kinetic or pitch-angle anisotropies, and an anti-sunward moving strahl (Pilipp et al. 1987; Pierrard et al. 2001a). The halo is dilute but can be much hotter than the core. The higher mobility of halo electrons must be reflected by the variations of their properties with the bulk speed and solar wind expansion. Radial profiles of electron properties in the ecliptic were provided by Pierrard et al. (2016), showing a monotonic decrease of the number density, for both the core and halo populations. However, a similar decrease in temperature with the distance from the Sun is only apparent for the core, while the halo temperature is slightly enhanced and then saturates, starting to decrease only beyond 3 AU. In the first in situ data recently transmitted by the Parker Solar Probe (PSP), suprathermal electrons show a similar flatness in temperature within ∼0.5 AU distance from the Sun (Moncuquet et al. 2020). Not only the temperature but also the suprathermalization of electron halo is enhanced, as shown by the decrease of κ-index with increasing the radial distance (Maksimovic et al. 2005; Pierrard et al. 2016). Lower values of κ correspond to stronger high-energy or suprathermal tails. In terms of the kinetic energy density that is quantified, for instance, by the plasma beta parameter (β= kinetic energy density/magnetic energy density 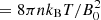=8πn k B T/ B 0 2 $ = 8\pi n{k_{\rm{B}}}T/B_0^2 $), we may therefore expect a reduced contrast between the halo (subscript h) and core (subscript c) populations, that is, comparable βh ∼ βc, unless a strong anticorrelation exists between the density and temperature of halo electrons.

On the other hand, the electron strahl is more prominent in high-speed winds with narrower angular widths and higher densities (Maksimovic et al. 2005; Anderson et al. 2012). Halo electrons remain however more dense than the strahl; the relative density increases with heliospheric distance, mainly at the expense of the electron strahl, and beyond 1 AU this relative density may exceed 10% of the total density (Maksimovic et al. 2005). The most plausible scenario involves the wave instabilities self-induced by the beaming electrons (see López et al. 2020 and references therein). The resulting enhanced fluctuations may pitch-angle scatter the electron strahl and stimulate their diffusion in velocity space, as shown by the observations (Hammond et al. 1996; Berčič et al. 2019). However, when the strahl becomes insignificant (under the instability thresholds), for example, in slow winds or for large enough heliospheric distances, the relative density of halo electrons is expected to decrease with increasing distance from the Sun.

We may therefore conjecture that properties of solar wind electrons, in particular those of halo populations are (highly) modulated by the solar wind bulk speed. Between 0.3 AU and 1.0 AU the electron core temperature exhibits a clear anticorrelation with the solar wind flow speed (Marsch et al. 1989), which is reconfirmed by the coronal data collected by the PSP mission at only 0.15–0.17 AU (Halekas et al. 2020; Maksimovic et al. 2020), supporting the hypothesis that the fast winds are dominated by subcoronal (cooler) plasmas escaping from coronal holes (Cranmer et al. 2002). Suprathermal electrons may organize themselves differently because their abundance is quantified not only by relative density but the power-law parameter κ. Early observations have associated the fast winds with lower values of κ but higher values of the electron plasma beta parameter (Maksimovic et al. 1997, 2000). This association suggests an increased suprathermalization that is most probably due to the presence of a strahl; the velocity distributions, measured in situ, were integrated over all pitch-angles and did not make a distinction between the halo and the drifting strahl. An abundance of suprathermals in the fast wind supports a hypothetical origin in the lower coronal layers, which is a critical condition for the velocity filtration to operate and overheat coronal plasma (Scudder 1992; Meyer-Vernet 2007). To be confirmed these hypotheses require, however, more detailed observational evidence. More recent studies of Helios data (Pierrard et al. 2016) show a reduced suprathermalization (κ >  6) of the halo electrons in the outer corona (∼0.3 AU), but do not make any distinction between the slow and high-speed winds. The origin of halo electrons is another fundamental question in heliophysics. For instance, the presence of these populations in the slow winds may be even more controversial. In this case, the electron halo may result from the concurrence of many dynamical or physical mechanisms, combining velocity filtration, Coulomb collisions, and particle acceleration or scattering by the kinetic turbulence and waves assumed at different levels in the corona (Pierrard et al. 2001b; Vocks et al. 2005; Che & Goldstein 2014).

In the present paper we examine the solar wind electron data collected by three spacecraft missions (Helios, Cluster, and Ulysses) from very low latitudes in the ecliptic (Štverák et al. 2008; Pierrard et al. 2016). The key properties of halo electrons and their connections with other plasma populations might be very subtle, but our purpose is to extract valuable insights from contrasting their evolutions with heliospheric distance in the slow and fast winds. The observational results presented in Sect. 2 include a comparison with the core population and are analyzed in conjunction with the existing knowledge of solar wind electron populations. In Sect. 3 we summarize the main conclusions, which aim to improve our understanding of the origin and implications of this population.

2. Halo electrons: Slow versus fast solar winds

The observed electron distributions combine a low-energy core (subscript c), a suprathermal halo (subscript h), and an asymmetric strahl (subscript s) drifting along the magnetic field, f(v) = ncfc(v)+nhfh(v)+nsfs(v, V0) (Pierrard et al. 2001a; Maksimovic et al. 2005). In general, the number densities of these three populations satisfy nc ≫ nh >  ns, as found in the slow or even fast winds between 0.3 and 4.0 AU (Maksimovic et al. 2005; Pierrard et al. 2016). Recent observations have also found the strahl dominating the suprathermal fraction of the distribution (ns >  nh), for example, for about 25 % of the upstream-only electrons near interplanetary shocks (Wilson et al. 2019a) or at perihelion near the Sun (Halekas et al. 2020). The quasi-thermal core corresponds to low energies up to a few tens of eV and is well reproduced by standard bi-Maxwellian models, while the suprathermal halo and strahl fall in an energy range extending up to 1 keV and are both well fitted by bi-Kappa or drifting Kappa distribution functions (Maksimovic et al. 2005; Štverák et al. 2008; Viñas et al. 2010; Nieves-Chinchilla & Viñas 2008).

In this section, we analyze the data set from Štverák et al. (2008), where the main properties of the core and halo electrons are quantified from a survey of 120 000 electron velocity distributions measured in the ecliptic by Helios 1 (0.3–1.0 AU, about 100 000 events), Cluster I (∼1.0 AU, about 10 000 events), and Ulysses (1.2–3.95 AU, about 14 000 events). The bi-Maxwellian core is described by three fitting parameters nc, Tc, ∥, and Tc, ⊥, while a bi-Kappa distributed halo involves four parameters, nh, κh = κ, Th, ∥, and Th, ⊥, where T∥, ⊥ denote parallel and perpendicular components of the temperature, defined with respect to the direction of (local) magnetic field. The relative drifts that these two populations may exhibit with respect to protons (even in the absence of strahl) are neglected, most probably because these drifts, if measurable, are in general small (Wilson et al. 2019a). The symmetry of the core and halo components allows us to separate these components from the anti-sunward moving strahl, and characterize them as described above; more details are provided in Štverák et al. (2008). The same set of events has been used by Pierrard et al. (2016) and Lazar et al. (2017) to characterize the temperatures and temperature anisotropies for both the core and halo populations. The halo electrons are contrasted with the low-energy core population for distinct conditions corresponding to the slow (VSW <  400 km s−1) and fast winds (VSW >  600 km s−1). The data set considered in this work also enables us to describe variations of the halo parameters with heliocentric distance in the ecliptic plane, computing their mean values within a number of radial bins centered on the following distances from the Sun 0.3, 0.5, 0.7, 0.95, 1.3, 2.7, 3.0, and 3.8 AU. There are always more observations at short than at large distances, but we consider data from a certain interval around the average distance in order to count for enough data.

2.1. κ-parameter

The power exponent κ is an inverse measure of the suprathermality (nonthermal departure from a Maxwellian) of halo electrons; high values signify populations approaching thermal equilibrium (κ → ∞), which are usually well described by a standard Maxwellian distribution function. Figure 1 presents the variation of κ with heliocentric distance, using the exact data (green dots) and average values determined for low (black) and high speed (red) winds. Error bars indicate standard deviations from the mean value1. The same style and significance of colors are adopted for all the observational plots in this paper.

thumbnail Fig. 1.

Spectral exponent κ of halo electrons as a function of radial heliocentric distance, in fast (red) and slow (black) winds.

Closer to the Sun, for example, R <  0.5 AU; the power-law parameter varies on a large interval, 3 ⩽ κ ⩽ 9 (see also Pierrard et al. 2016), but the highest values dominate, that is, κ >  6, showing a less suprathermalized (or more thermalized) halo. The parameter κ decreases with increasing the distance from the Sun, which agrees with other observations, for example, in Maksimovic et al. (2005). This decrease of κ cannot be explained by the simple expansion of the solar wind, but suggests the existence of an additional source of suprathermalization in interplanetary space, for example, self-generated plasma instabilities (Gary & Saito 2007; Berčič et al. 2019; López et al. 2020), which may scatter the electron strahls, and, implicitly, enhance the halo population. This would explain the steeper suprathermalization of halo electrons in the fast winds, when the strahl is in general more prominent (see also the discussions in Sect. 2.2).

Lower values of κ are more specific to the fast winds up to 1.3 AU, which may be an indication of their sub-coronal origin, as also suggested by the Ulysses observations over the polar coronal holes. We should remember that this κ parameter exclusively characterizes the halo population because the strahl is excluded by the fitting method applied to model and quantify the observed distributions (Štverák et al. 2008). Coronal holes with a more reduced size can also be present at lower latitudes, even close to the equator (see Fig. 8 in Pierrard & Pieters 2014), and may therefore explain the fast wind typical data at low distances in the outer corona. The difference between κ-values in the fast and slow winds increases with distance (e.g., from 0.3 to 0.7 AU) most probably from an increasing mixture with the polar fast wind populations. This is also suggested by a steeper decrease of κ in the fast winds, which continues monotonically with the expansion up to 4 AU. At about 0.7 AU the slow wind halo undergoes a pronounced suprathermalization, which stagnates at about 1.3 AU and then it diminishes beyond 3 AU. The interval between 1.3 AU and 2.3 AU, where the slow wind κ decreases slightly under the average values obtained in the fast wind, is remarkable. For exactly the same interval of heliospheric distances but at high latitudes (between 49° S and 82° S) in the southern hemisphere, Hammond et al. (1996) found a substantial broadening of the strahl associated with the fast winds. Scattering by the self-induced fluctuations have also been invoked, being also consistent with a reduction of the electron heat flux (mainly carried by suprathermal electrons) with increasing heliocentric distance. However, such a motivation is not appropriate for the slow wind profiles in Fig. 1. In subsequent sections, we seek further explanations of this non-monotonic variation of κ through a direct corroboration with the evolutions of other parameters.

2.2. Electron densities

If κ is an inverse measure of suprathermality, the number density (nh) quantifies the abundance of halo electrons directly. The top panel in Fig. 2 shows the decrease of halo density nh with heliocentric distance. From low radial distances up to 1 AU, this population is significantly represented in the slow winds, with densities reaching significant values and sometimes exceeding nh >  10 cm−3, while in the fast wind nh may be even one order of magnitude lower. In the slow wind halo electrons are denser and more thermalized (i.e., with higher κ) than in the fast wind. It seems fairly intuitive that higher densities must correspond to a more thermalized (less suprathermalized) halo. We note, however, that toward the Sun the PSP data indicate a different trend for the halo density, which remains relatively constant or even decreases with decreasing distance, that is, from 0.4 AU to 0.17 AU (Halekas et al. 2020).

thumbnail Fig. 2.

Electron halo density in cm−3 (top) and the relative halo-core density nh/nc (bottom) as functions of radial heliocentric distance, in fast (red) and slow (black) winds.

At large heliospheric distances beyond 1 AU these anticorrelations are reduced, and switch to a positive correlation between nh and the solar wind bulk speed, which is visible in the interval 1.3  AU <  R <  3.0 AU. For even larger distances (e.g., > 3 AU) nh again becomes favorable to slow winds. These variations correspond, showing consistency, with a similar oscillatory variation of κ in Fig. 1. In particular, changes leading to higher halo densities in the fast winds are associated with the same interval of radial distances, 1.3 AU <  R <  3.0 AU, already outlined above, and by Hammond et al. (1996) but within high-latitude data also reported by Ulysses. In the fast winds the halo can be enhanced by a redistribution of beaming (or strahl) electrons, under the effects of self-generated instabilities leading to their pitch-angle scattering and diffusion in velocity space. It seems that these processes reach their apogee in the same interval of radial distances where both the halo density and κ become directly correlated with the flow speed of the solar wind. On the other hand, if the strahl (or heat-flux) instabilities are at the origin of this non-monotonic evolution of the halo properties, one should understand why their effects are not evident at lower heliospheric distances, where the strahl is more pronounced (Maksimovic et al. 2005; Berčič et al. 2019). An immediate explanation would be that at low radial distances the scattering by self-generated fluctuations and by the particle-particle collisions may still be counterbalanced by self-focusing from the adiabatic expansion along a decreasing magnetic field. The effects of collisions and adiabatic expansion decrease with distance; the mean values of nh in Fig. 2 show a slower decrease beyond 0.5 AU.

The bottom panel in Fig. 2 shows the relative halo-core (fractional) densities, nh/nc, whose values closest to the Sun agree well with the halo fractional density measured by the PSP mission between 0.17 AU and 0.4 AU (Halekas et al. 2020). The sharp limitation upper (up to 1 AU), or even lower (for lower distances) shown by this fractional density is very intriguing; this suggests the existence of some constraints in the fitting method used by Štverák et al. (2008), although these authors did not mention anything like that. Our mean values show however significant differences in slow winds compared to high-speed winds; this is because within 1 AU this density ratio is higher in slow winds, even several times higher than mean values obtained in the fast winds. But this contrast slightly decreases with increasing radial distance, especially beyond 0.5 AU, and then shows the same switching location, at 1.3 AU. For larger distances the relative halo-core density (nh/nc) becomes higher in the fast winds and remains so up to 4 AU, when the contrast between the slow and fast winds becomes minimal. These variations show a reasonable correspondence with the variations of κ and nh, and may be explained, most probably, by the same transformations of halo electrons in the fast winds.

2.3. Electron temperatures

Figure 3 indicates temperatures of the halo electrons, Th (top), and the halo-core temperature ratio, Th/Tc (bottom), for the slow and fast winds. At relatively low distances (R <  1 AU) halo electrons show only a modest anticorrelation in temperature with solar wind speed because the halo is only slightly cooler in the fast winds, most probably as a consequence of their sub-coronal origin. In the slow winds the halo temperature is characterized by an extended flatness, similar to PSP observations at very low (< 0.5 AU) distances (Moncuquet et al. 2020), and exhibits a slight increase beyond 0.7 AU. This radial profile of the halo temperature is also consistent with the variation of κ in Fig. 1 (see also Lazar et al. 2017). The fast winds show the same non-monotonic variation, this time for the halo temperature, which markedly increases beyond 1.0 AU. Maksimovic et al. (2020) have also reported a direct correlation between total temperature of electrons and solar wind speed at about 1 AU.

thumbnail Fig. 3.

Halo temperature Th (top) and halo-core temperature ratio Th/Tc (bottom) as functions of radial heliocentric distance, in fast (red) and slow (black) winds.

At large distances from the Sun the halo electrons are hotter in the fast winds, with the highest contrast corresponding to the same interval 1.3 AU <  R <  3.0 AU, already associated with some intriguing transformations of this population. However, this significant contrast is mainly generated by the peaking Th values obtained at about 2.7 AU, but with a reduced amount of data. We can therefore suspect the presence of some transient events, like interplanetary coronal mass ejections (ICMEs), when the temperature of suprathermal electrons may be positively correlated with density (Skoug et al. 2000). Corresponding to the same location, in Fig. 2 the fast winds exhibit only a modest excess of halo density nh (top panel), but a significantly higher density ratio nh/nc (bottom panel), which may support this hypothesis.

The quasi-adiabatic cooling of the core electrons becomes evident, indirectly, from the plots in the bottom panel of Fig. 3, which show a systematic increase of the halo-core temperature ratio, Th/Tc, with heliospheric distance, for both the slow and high-speed winds. However, this ratio is in general higher in the fast winds, indicating a higher temperature contrast between halo and core electrons, presumably from the redistribution of electrons from the strahl into the halo. The redistribution of electrons from the strahl should operate at any distance, involving fewer electrons that are hotter at lower distances, and more electrons that are cooler at higher distances, such that, their overall contribution makes the difference in the radial profiles of the slow and fast winds. These differences have not been reported yet, at least to our knowledge, with the exception that the electron core was also found to be cooler in the fast winds (Marsch et al. 1989). Green data dots show a very hot halo at large distances, beyond 1AU, where the halo temperature can exceed more than ten times that of the core. At about 2.7 AU the variation of Th/Tc remains monotonic, without any irregularities that may witness a transient ICME eventually captured in our data.

2.4. Electron plasma betas

Plasma beta (β) gives a measure of the kinetic energy density of plasma particles with respect to the mean magnetic field energy density (see in the introduction). It is widely invoked to define various macro- and microscopic regimes of magnetized plasmas, and for studying physical processes conditioned by the departure from the equipartition of energy (β ∼ 1). In Fig. 4 we show the halo plasma beta, βh (top panel), and the ratio contrasting the halo beta with the core beta, βh/βc (bottom).

thumbnail Fig. 4.

Halo electron beta βh (top) and halo-core electron beta ratio βh/βc (bottom) as functions of the radial heliocentric distance, in fast (red) and slow (black) winds.

The halo plasma beta shows a significant anticorrelation with the solar wind speed, for a slightly extended range of radial distances, from 0.3 AU up to 1.5 AU. The largest number of events analyzed in this work (roughly 110 000 green dots) are those detected in the interval (0.3–1.0) AU of relatively low distances, where the halo beta may vary more than three orders of magnitude. It spreads between the lowest limit (i.e., βh ∼ 0.001), which is characteristic of the high-speed winds at lower distances and the highest limits exceeding βh ⩾ 10 at (0.8–0.95) AU. These results are consistent with other recent studies of Helios data that show the same anticorrelation, by associating lower-beta electrons with faster winds (Berčič et al. 2019). Moreover, the mean values in the slow winds are higher than those obtained for the fast winds, the difference often exceeding one order of magnitude. However, the same increasing trend shown by the mean values at low distances (< 1 AU) continues only for the fast wind up to 3 AU. Instead, in the slow winds the halo beta becomes lower at large radial distances (i.e., > 1 AU), and stabilizes with mean values slightly oscillating around 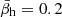β ¯ h = 0.2 $ \bar{\beta}_{\mathrm{h}} = 0.2 $, but always less than those obtained in the fast wind.

The electron beta ratio, βh/βc, shows similar trends as in the top panel, with an anticorrelation with the solar wind speed visible at low radial distances (< 1 AU), while for larger distances this ratio becomes favorable to the fast winds. At low distances green dots show a βh much lower than βc. Contrary to previous estimations (Maksimovic et al. 2000) and to the increasing trend with heliospheric distance, the halo beta remains inferior to the core beta (i.e., βh <  βc), from 0.3 to 4 AU. The same conclusion applies to the corresponding kinetic energy densities, meaning that nhTh <  ncTc. Earlier estimations of the same ratio βh/βc = nhTh/ncTc suggested a lower contrast between halo and core, especially in the fast wind, where very often βh was found to be even higher than βc (Maksimovic et al. 2000). These overestimations may be explained by the fact that Maksimovic et al. (2000) used moments of distributions obtained not from exact fits but via numerical integration of the Ulysses data with a series of corrections (for the spacecraft potential) and adjustments (to the energy breakpoints from inflections in the spectral shape), which allowed these authors to differentiate and approximate the core and halo components (Bame et al. 1992; Scime et al. 1994). The profiles shown by βh and βh/βc are similar to those obtained above for the density and temperature and may also reflect the presence of a transient ICME in our data at about 2.7 AU.

2.5. Temperature anisotropies

Measurements in the radial interval from 1.3 to 3.0 AU seem boosted by some transient events such as ICMEs, which can induce specific signatures in the velocity distributions of suprathermal electrons and modulate their properties. Fast flows guided by the closed magnetic field topologies lead to specific counterbeaming, field-aligned strahls, often reported during an ICME passage. The technique used to obtain our data set is designed to separate the core and halo electrons from an asymmetric strahl (Štverák et al. 2008), but does not apply for double or counter-beaming strahls, which are more or less symmetric. We may therefore expect that electron counter-beams, if present, would mimic an excess of (kinetic) temperature in a parallel direction (Wimmer-Schweingruber et al. 2006). The Ulysses data used in the present analysis are measured in 1990 and 1991 (Štverák et al. 2008), but we do not know exactly the dates, making thus impossible a direct comparison with the existing catalogs of ICMEs (see, e.g., Du et al. 2010). However, the probability of having an ICME event captured in our data increases if these effective anisotropies of the electron halo corroborate well with other specific signatures of ICMEs, such as enhanced thermal and suprathermal populations with enhanced (effective) temperatures, already described in the previous sections.

In this section we describe the anisotropy of halo temperature, focusing the analysis on the radial interval (1.3–3.0) AU, where we already found enhancements of density and temperature of the halo population in the fast winds. The anisotropy is defined by A = T⊥/T∥, the ratio of perpendicular and parallel components in temperature, where ⊥ and ∥ are defined with respect to the direction of local magnetic field. Figure 5 represents anisotropies for both the halo (subscript h, top panel) and the core (subscript c, bottom panel) populations. Comparing the distributions of data dots, we find that halo electrons show deviations from isotropy in both directions, more or less proportional, either in perpendicular (Ah >  1) or parallel (Ah <  1) directions. Instead the core shows, more predominantly, a parallel anisotropy (Ac <  1); these results are in perfect qualitative agreement with those presented by Štverák et al. (2008) and Pierrard et al. (2016).

thumbnail Fig. 5.

Temperature anisotropy of the halo electrons Ah (top) and the core electrons Ac (bottom) as functions of radial heliocentric distance, in fast (red) and slow (black) winds.

Mean values show the difference between the slow (black) and fast (red) winds, with a systematic anticorrelation of both the halo and core anisotropies with the bulk speed of the solar wind. There is only one short exception, at about 1 AU, when the mean values of the halo anisotropies in the slow and high-speed winds become comparable. In the slow winds the mean values of anisotropy, for both the core and halo components, align near the isotropy conditions (Ac, h ≃ 1), due to a symmetric distribution of anisotropies in perpendicular (A >  1) and parallel (A <  1) directions (see also Štverák et al. 2008 and Pierrard et al. 2016). In the fast winds predominant are parallel anisotropies (Ac, h <  1), which suggests a possible influence of strahls, double strahls, or counterbeaming electrons present not only in ICMEs, but any interplanetary shock and region of corotating interaction between fast and slow winds. The mean value and corresponding standard deviations obtained at about 2.7 AU in the fast winds show an excess of anisotropy in parallel direction, which can result under the influence of counterbeaming field-aligned strahls, specific to ICMEs.

3. Conclusions

In the present paper we have revisited the solar wind electron data collected by three spacecraft missions from different heliospheric distances between 0.3 and 0.4 AU in the ecliptic. The electron parameters were obtained from fitting the central (non-drifting) part of the observed velocity distributions (after removing the asymmetric strahl) with a dual model, which makes a clear distinction between the quasi-thermal core, described by a standard bi-Maxwellian model, and the suprathermal halo, reproduced by a generalized bi-Kappa (or bi-κ) distribution function (Štverák et al. 2008). The present analysis focused on suprathermal halo population, which is ubiquitous in space plasmas, but is insufficiently examined. We described the main properties of halo electrons, that is, spectral power parameter κ, number density, temperature, plasma beta, and temperature anisotropy, contrasting their variations with heliospheric distance in the slow and fast winds, and also comparing these properties with the corresponding parameters of the core electrons.

The results of our analysis can be summarized as follows.

At relatively low radial distances, i.e., < 1 AU, all the parameters characterizing the halo electrons show an anticorrelation with the solar wind speed. For an immediate explanation, we may presume that high-speed streams originate in the lower coronal layers, where plasmas have densities and temperatures below those already measured in the upper corona. This contrast between halo properties in the slow and fast winds decreases as distance from the Sun increases and may switch to a positive correlation beyond 1 AU.

In the outer corona (≳0.3 AU), the fast wind shows a higher suprathermalization (lower values of κ) than slow wind (Fig. 1). This result supports the hypothetical presence of suprathermal electrons in the lower corona, and implicitly supports the mechanisms of velocity filtration, which explains coronal plasma overheating (Scudder 1992; Meyer-Vernet 2007), and solar wind acceleration (Zouganelis et al. 2005).

The parameter κ decreases with increasing distance from 0.3 to 0.7 AU (Fig. 1), suggesting the existence of a suprathermalization mechanism (e.g., energization of electrons by interaction with kinetic plasma waves and turbulent fluctuations) that surpasses the thermalization effect of binary collisions (Pierrard et al. 2011). This suprathermalization is somewhat stronger in the fast winds, being probably stimulated by the wave fluctuations self-generated by the strahl (or heat-flux) instabilities. If the solar wind electrons are hot and tenuous enough, their suprathermal populations are collisionless (Wilson et al. 2018, 2019a), but in the community there are opinions often invoking collisions, or collisional age of plasma populations (Salem et al. 2003), to explain their dominant (peaking) presence at or near the states of isotropic temperature (Štverák et al. 2008); see also our Fig. 5. Suprathermals are energized and entertained by a certain level of wave turbulence, but their accumulation near isotropy together with a dominant quasi-thermal (Maxwellian) core in the electron distributions seem to be reminiscent of a more collisional nature. This hypothesis is also supported by the results finding near-Maxwellian halo distributions closer to the Sun or in the outer corona (see Fig. 1 and some results in Maksimovic et al. 2005; Pierrard et al. 2016; Halekas et al. 2020).

Thermalization factors (e.g., binary collisions) diminish with increasing distance from the Sun, explaining a steeper decrease of κ in the slow winds beyond 0.7 AU. This can be correlated with a steeper decrease of density in Fig. 2, which is more apparent beyond 0.95 AU, suggesting that solar wind expansion may also induce an effective suprathermalization of the halo electrons. In the slow winds the halo temperature (Fig. 3) exhibits a modest increase that is also consistent with the variation of κ; see also Lazar et al. (2017).

The fast winds can be markedly affected by the self-generated (electron beaming) instabilities and transient energetic events such as ICMEs, which may determine the observed highly non-monotonic variations of halo properties (temperature and number density of halo electrons, plasma beta, and temperature anisotropy).

At low distances in the fast winds the halo does not gain much from a redistribution of beaming or strahl electrons, and the number density (nh) shows a steeper decrease with the solar wind expansion (Fig. 2). This becomes apparent with increasing the radial distance, beyond 0.5 AU, when adiabatic focusing is weak and cannot counterbalance the diffusion of strahl electrons, triggered mainly by the interactions with (self-generated) wave fluctuations.

The halo temperature (Th, Fig. 3) and the plasma beta parameter (βh, Fig. 4) show similar radial profiles in the fast winds. These two parameters increase with increasing the distance from the Sun, especially beyond 0.5 AU, which may be the consequence of the same scattering (in pitch angle and energy) of strahl electrons. This tendency is however accentuated after 1.3 AU, eventually, by a transient energetic event, for example, an ICME, peaking the values of these parameters at 2.7 AU for Th and 3.0 AU for βh. This hypothesis seems to be supported by a series of specific ICME signatures shown by the number density, temperature, and temperature anisotropy Th, ∥ >  Th, ⊥ (mimicked by the counterbeaming strahls present in the closed magnetic field topologies of ICMEs).

With or without this event the increase of these parameters seems to be saturated at 3.0 AU. Interestingly, Hammond et al. (1996) studied similar fast wind data from Ulysses, but from high latitudes, and they found a substantial scattering of the strahl in the interval 1.3–3.0 AU. Moreover, Maksimovic et al. (2005) combined fast wind data from ecliptic and high-latitudes and found that the relative density of the halo already starts to increase at 0.5 AU, and on the expense of the strahl relative density. Our results show a progressive enhancement of halo electrons and their properties between 0.5 AU and 3.0 AU in the fast winds, supporting the idea that significant fractions of strahl electrons and (kinetic) energy are redistributed and transferred to the halo population.

Understanding these evolutions requires advanced theories and multi-scale modeling to combine exospheric mechanisms involving suprathermal electrons (e.g., velocity filtration), and effects of solar wind expansion (e.g., magnetic focusing and increase of parallel temperature) with diffusion in pitch angle and energy induced by collisions (at low distances in the outer corona) and by wave-particle interactions (Zouganelis et al. 2005; Tigik et al. 2016; Innocenti et al. 2019).

1

When the distribution of data is not Gaussian in nature the representation of data distribution at each radial distance may be improved using the median and quartiles (Wilson et al. 2019a,b), but we adopt a generally used method of characterization of their mean value and standard deviations.

Acknowledgments

The authors acknowledge useful discussions during the working meetings of the project “Kappa Distributions”, hosted by the International Space Science Institute (ISSI) in Bern. The authors are also grateful to S. Štverák and M. Maksimovic for providing the observational data. These results were obtained in the framework of the projects SCHL 201/35-1 (Deutsche Forschungsgemeinschaft, DFG), and G0A2316N (FWO-Vlaanderen).

References

  1. Anderson, B. R., Skoug, R. M., Steinberg, J. T., & McComas, D. J. 2012, J. Geophys. Res.: Space Phys., 117 [Google Scholar]
  2. Bame, S. J., McComas, D. J., Barraclough, B. L., et al. 1992, A&AS, 92, 237 [NASA ADS] [Google Scholar]
  3. Berčič, L., Maksimović, M., Land i, S., & Matteini, L. 2019, MNRAS, 486, 3404 [NASA ADS] [CrossRef] [Google Scholar]
  4. Che, H., & Goldstein, M. L. 2014, ApJ, 795, L38 [NASA ADS] [CrossRef] [Google Scholar]
  5. Collier, M. R., Hamilton, D. C., Gloeckler, G., Bochsler, P., & Sheldon, R. B. 1996, Geophys. Res. Lett., 23, 1191 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cranmer, S. 2002, in Multi-wavelength Observations of Coronal Structure and Dynamics, eds. P. C. Martens, & D. P. Cauffman (Pergamon), COSPAR Colloquia Ser., 13, 3 [Google Scholar]
  7. Du, D., Zuo, P. B., & Zhang, X. X. 2010, Sol. Phys., 262, 171 [NASA ADS] [CrossRef] [Google Scholar]
  8. Gary, S. P., & Saito, S. 2007, Geophys. Res. Lett., 34, L14111 [CrossRef] [Google Scholar]
  9. Halekas, J. S., Whittlesey, P., Larson, D. E., et al. 2020, ApJS, 246, 22 [Google Scholar]
  10. Hammond, C. M., Feldman, W. C., McComas, D. J., Phillips, J. L., & Forsyth, R. J. 1996, A&A, 316, 350 [Google Scholar]
  11. Innocenti, M. E., Tenerani, A., Boella, E., & Velli, M. 2019, ApJ, 883, 146 [CrossRef] [Google Scholar]
  12. Lazar, M., Schlickeiser, R., & Poedts, S. 2012, in Exploring the Solar Wind, (Rijeka: IntechOpen) [CrossRef] [Google Scholar]
  13. Lazar, M., Pierrard, V., Shaaban, S., Fichtner, H., & Poedts, S. 2017, A&A, 602, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. López, R. A., Lazar, M., Shaaban, S. M., Poedts, S., & Moya, P. S. 2020, ApJ, 900, L25 [CrossRef] [Google Scholar]
  15. Maksimovic, M., Pierrard, V., & Riley, P. 1997, Geophys. Res. Lett., 24, 1151 [NASA ADS] [CrossRef] [Google Scholar]
  16. Maksimovic, M., Gary, S. P., & Skoug, R. M. 2000, J. Geophys. Res.: Space Phys., 105, 18337 [NASA ADS] [CrossRef] [Google Scholar]
  17. Maksimovic, M., Zouganelis, I., Chaufray, J.-Y., et al. 2005, J. Geophys. Res., 110 [Google Scholar]
  18. Maksimovic, M., Bale, S. D., Berčič, L., et al. 2020, ApJS, 246, 62 [CrossRef] [Google Scholar]
  19. Marsch, E., Pilipp, W., Thieme, K., & Rosenbauer, H. 1989, J. Geophys. Res.: Space Phys., 94, 6893 [NASA ADS] [CrossRef] [Google Scholar]
  20. Meyer-Vernet, N. 2007, Basics of the Solar Wind, Cambridge Atmospheric and Space Science Series (Cambridge University Press) [Google Scholar]
  21. Moncuquet, M., Meyer-Vernet, N., Issautier, K., et al. 2020, ApJS, 246, 44 [CrossRef] [Google Scholar]
  22. Nieves-Chinchilla, T., & Viñas, A. F. 2008, J. Geophys. Res. (Space Phys.), 113, A02105 [NASA ADS] [CrossRef] [Google Scholar]
  23. Pierrard, V., & Lazar, M. 2010, Sol. Phys., 267, 153 [NASA ADS] [CrossRef] [Google Scholar]
  24. Pierrard, V., & Pieters, M. 2014, J. Geophys. Res.: Space Phys., 119, 9441 [NASA ADS] [CrossRef] [Google Scholar]
  25. Pierrard, V., Maksimovic, M., & Lemaire, J. 2001a, Ap&SS, 277, 195 [CrossRef] [Google Scholar]
  26. Pierrard, V., Maksimovic, M., & Lemaire, J. 2001b, J. Geophys. Res., 106, 29,305 [NASA ADS] [CrossRef] [Google Scholar]
  27. Pierrard, V., Lazar, M., & Schlickeiser, R. 2011, Sol. Phys., 269, 421 [NASA ADS] [CrossRef] [Google Scholar]
  28. Pierrard, V., Lazar, M., Poedts, S., et al. 2016, Sol. Phys., 291, 2165 [NASA ADS] [CrossRef] [Google Scholar]
  29. Pilipp, W. G., Miggenrieder, H., Mühlhaüser, K. H., et al. 1987, J. Geophys. Res., 92, 1103 [NASA ADS] [CrossRef] [Google Scholar]
  30. Salem, C., Hubert, D., Lacombe, C., et al. 2003, ApJ, 585, 1147 [NASA ADS] [CrossRef] [Google Scholar]
  31. Scime, E. E., Phillips, J. L., & Bame, S. J. 1994, J. Geophys. Res., 99, 14769 [CrossRef] [Google Scholar]
  32. Scudder, J. D. 1992, ApJ, 398, 299 [NASA ADS] [CrossRef] [Google Scholar]
  33. Skoug, R. M., Feldman, W. C., Gosling, J. T., McComas, D. J., & Smith, C. W. 2000, J. Geophys. Res., 105, 23069 [NASA ADS] [CrossRef] [Google Scholar]
  34. Tigik, S. F., Ziebell, L. F., Yoon, P. H., & Kontar, E. P. 2016, A&A, 586, A19 [CrossRef] [EDP Sciences] [Google Scholar]
  35. Štverák, Š., Trávníček, P., Maksimovic, M., et al. 2008, J. Geophys. Res., 113, A03103 [Google Scholar]
  36. Vasyliunas, V. M. 1968, J. Geophys. Res., 73, 2839 [NASA ADS] [CrossRef] [Google Scholar]
  37. Viñas, A. F., Gurgiolo, C., Nieves-Chinchilla, T., Gary, S. P., & Goldstein, M. L. 2010, AIP Conf. Proc., 1216, 265 [Google Scholar]
  38. Vocks, C., Salem, C., Lin, R. P., & Mann, G. 2005, ApJ, 627, 540 [NASA ADS] [CrossRef] [Google Scholar]
  39. Wilson, L. B., Stevens, M. L., Kasper, J. C., et al. 2018, ApJS, 236, 41 [NASA ADS] [CrossRef] [Google Scholar]
  40. Wilson, L. B., Chen, L.-J., Wang, S., et al. 2019a, ApJS, 245, 24 [CrossRef] [Google Scholar]
  41. Wilson, L. B., Chen, L.-J., Wang, S., et al. 2019b, ApJS, 243, 8 [CrossRef] [Google Scholar]
  42. Wimmer-Schweingruber, R. F., Crooker, N. U., Balogh, A., et al. 2006, Space Sci. Rev., 123, 177 [Google Scholar]
  43. Zouganelis, I., Meyer-Vernet, N., Landi, S., Maksimovic, M., & Pantellini, F. 2005, ApJ, 626, L117 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Spectral exponent κ of halo electrons as a function of radial heliocentric distance, in fast (red) and slow (black) winds.
In the text
thumbnail Fig. 2.

Electron halo density in cm−3 (top) and the relative halo-core density nh/nc (bottom) as functions of radial heliocentric distance, in fast (red) and slow (black) winds.
In the text
thumbnail Fig. 3.

Halo temperature Th (top) and halo-core temperature ratio Th/Tc (bottom) as functions of radial heliocentric distance, in fast (red) and slow (black) winds.
In the text
thumbnail Fig. 4.

Halo electron beta βh (top) and halo-core electron beta ratio βh/βc (bottom) as functions of the radial heliocentric distance, in fast (red) and slow (black) winds.
In the text
thumbnail Fig. 5.

Temperature anisotropy of the halo electrons Ah (top) and the core electrons Ac (bottom) as functions of radial heliocentric distance, in fast (red) and slow (black) winds.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.