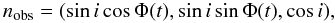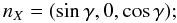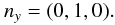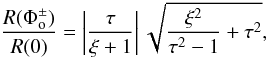| Issue |
A&A
Volume 536, December 2011
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201116981 | |
| Published online | 09 December 2011 | |
Theoretical light curves of dipole oscillations in roAp stars
1
Université Nice Sophia Antipolis, Observatoire de la Côte d’Azur, Département Cassiopée CNRS/UMR 6202, BP 4229, 06304 Nice, France
e-mail: lbigot@obs-nice.fr
2
Jeremiah Horrocks Institute of Astrophysics, University of Central Lancashire, Preston PR1 2HE, UK
Received: 30 March 2011
Accepted: 2 September 2011
Context. The dipole modes are the most common geometry of oscillations in roAp stars inferred from photometric measurements and are therefore of special interest for asteroseismic purposes.
Aims. We present a theoretical and analytical study of the light curves associated with dipole (ℓ = 1) pulsations of roAp stars in the framework of the revisited oblique pulsator model.
Methods. We describe the light curves in terms of the inclination and polarization of the elliptical displacement vector of the dipole modes. We study the influence of the magnetic field and rotation on the shape of these light curves for both amplitudes and phases.
Results. Despite the inclination of dipole mode with respect to the magnetic axis, we find that the dipole mode can have maxima that are in phase with the magnetic maxima. We apply our formalism to the well-known roAp star HR 3831 (HD 83368) to derive its mode properties. Our results are similar to those obtained by time-series spectroscopy. We also consider the cases of three other roAp stars, HD 6532, HD 99563, and HD 128898 (α Cir).
Conclusions. We demonstrate that the formalism of the revisited oblique pulsator model is adequate to explain the properties of the photometric light curves associated with dipole modes in roAp stars. In addition, we show that the coincidence of pulsation and magnetic extrema can also occur for inclined modes with respect to the magnetic axis. With the stars considered in this paper, we conclude that the polarization of the modes present in roAp stars are quasi linearly polarized.
Key words: stars: oscillations / stars: chemically peculiar / stars: variables: general / stars: magnetic field
© ESO, 2011
1. Introduction
It is well-known that the rapid light variations in Ap stars are caused by trapped magneto-acoustic modes. The first detection of these oscillations was made by Kurtz (1978, 1982), who clearly showed the presence of high radial order modes (n ≈ 20−30) with periods comparable to those of the solar-like stars; these periods are now known to range from 6 to 21 min. The photometric amplitudes of the roAp stars, with values of about 0.1 − 8 mmag, are vastly higher than those of the solar-like oscillators. It is now common to refer to these objects as roAp stars, for rapidly oscillating Ap stars. To date, over 40 roAp have been detected, Kurtz et al. (2006) listing 40 of them.
We can distinguish three fundamental properties of the photometric variability of these stars:
-
1.
The light curves of many roAp stars show a double modulation.The rapid one, with a period of a few minutes, arises from thepulsation modes. The long one, with a period between days anddecades, is the rotation period of the star. To explain the presenceof the long-term variation, Kurtz (1982) proposed that thepulsation mode axis is aligned with the magnetic axis, which isitself inclined to the rotation axis so that the observer sees thepulsation modes from an aspect that varies with rotation. This isthe oblique pulsator model.
-
2.
The second main property of the roAp stars is that the maxima of the rotational amplitude modulation of the pulsations occur at the same rotation phases as that of the magnetic maxima. This observational finding led Kurtz (1982) to justify the inclination of the modes with the rotation axis, simply by considering a pulsation axis aligned with the magnetic one. In the magnetic Ap stars, it is indeed well-known that the magnetic and rotation axes are inclined with respect to each other (e.g. Landstreet & Mathys 2000); this is the oblique rotator model (Stibbs 1950). Kurtz’s explanation looked reasonable given the huge, kG-strength magnetic fields observed at the surface of these stars, at least two or three orders of magnitudes higher than the global magnetic field of the Sun.
-
3.
Finally, the last main property derived from photometry is that for some of the roAp stars – those with geometries such that both magnetic poles come into view over the rotation period – the light curves show a phase jump of ± π radians as the pulsation amplitude passes through a minimum. This property is most easily explained when the geometrical structure of the mode consists of two hemispheres with opposite phases, say a dipole (ℓ = 1) mode, although other, higher spherical degree modes may show the same effect for certain viewing geometries.
Over the past two decades, many theoretical investigations have studied the properties of the roAp stars. The purely geometrical model of Kurtz was improved by considering the effects of both the magnetic field and rotation (Dziembowski & Goode 1985; Kurtz & Shibahashi 1986; Shibahashi & Takata 1993; Takata & Shibahashi 1995). However, despite these improvements, the magnetic field treatment in all these studies was oversimplified. They indeed considered a perturbative treatment to solve the magnetic effects in the problem, which is unrealistic because in the outer layers of the star the magnetic pressure is higher than the gas pressure.
In these models, the modes were found to be aligned (or nearly aligned) with the magnetic field, in agreement with Kurtz’s original proposition of aligned pulsation and magnetic axes. The reason behind this alignment is that for high overtone pulsations, the magnetic perturbation is much larger than the Coriolis one.
On the basis of both photometric observations and theoretical properties, the picture of the pulsations in roAp stars over the past two decades has been that of dipole oscillations with the pulsation axis aligned with the magnetic axis. The inclination of these with respect to the rotation axis thus explains the observed long-term modulation of the pulsation amplitude.
Bigot & Dziembowski (2002) proposed an alternative description of pulsations in roAp stars. They found that the axis of pulsation can be inclined by a large angle to the magnetic axis. This result comes from a degenerate perturbative treatment of the rotation effects for which they added the quadratic effect of the centrifugal force in the problem. This second order effect of rotation was considered negligible in previous studies. For high radial order modes, such as those in roAp stars, the centrifugal effects can be comparable to the effect of the magnetic field. These improvements are crucial for quantitative studies and can change the inclination of the mode.
For relatively moderate fields, unlike in the previous studies, there is no dominant perturbation acting on the mode, but rather a balance between magnetic and rotational perturbations. In their formalism, Bigot & Dziembowski (2002) showed that in the case of dipole modes the pulsation axis lies in a plane during the pulsation cycle, with a displacement vector moving with an elliptical motion. These dipole modes are fully characterized by three quantities: the inclination of the mode plane, the ellipticity of the displacement vector, and the frequency. Bigot and Dziembowski applied their model to the roAp star HR 3831 and based on the magnetic measurements (Bagnulo et al. 1999), they showed that, for this star, the mode axis is well inclined to both the magnetic and rotation axes.
Considerable progress has since been made in the understanding of pulsation in roAp stars by analysing spectroscopic time-series observations. In particular, those lead to the possibility of probing the vertical structure of pulsation through the atmospheric layers by analysing the pulsation through different lines that form at different atmospheric depths. The multiplets observed in spectroscopy do not look like those derived by photometry, but have instead stronger non-dipolar components. Kochukhov (2006) derived a new geometrical aspect of the mode of HR 3831 using radial velocity measurements and found no significant inclination with respect to the magnetic axis. Therefore, he returned to the original proposition of Kurtz (1982) and thus questioned the results of Bigot & Dziembowski (2002).
The main objective of this paper is to provide an observational counterpart to the model developed in Bigot & Dziembowski (2002). We derive a formalism to calculate analytical light curves associated with an arbitrary combination of dipole modes (m = −1,0, + 1). The relatively simple geometrical model that we propose is particularly useful for analysing photometric pulsation data. We see that it closely agrees with both photometric and radial velocity observations.
In Sect. 2, we give an analytical expression for the light curves of dipole modes in terms of the formalism proposed by Bigot & Dziembowski (2002), i.e. the mode inclination and polarization. In Sect. 3, we discuss the correlation between the dipole mode inclination and coincidence of pulsation and magnetic extrema. In Sect. 4, we consider the effects of a changing magnetic field on these light curves and how it affects their amplitudes and phases. Finally, in Sect. 5 we apply these new considerations to the cases of four roAp stars HR 3831, HD 6532, α Cir, and HD 99563. We see that our formalism agrees well with observations. For the particular case of HR 3831, in the light of a new measurement of the inclination angle of the observer, we show that our formalism leads to results that are consistent with those of Kochukhov (2006) within the formalism presented in the oblique pulsator model of Bigot & Dziembowski (2002).
2. The light curve variations of dipole modes
2.1. A general expression for non-radial oscillations
The formalism for light variations in the case of non-radial oscillations is given in Dziembowski (1977; see also Buta & Smith 1979). We follow the formulation of Dziembowski, but with an additional approximation specific to roAp stars. In the case of high radial orders, the main contribution of the fluctuations to the luminosity δL comes from the variations in the radiative flux δℱ. We can reasonably ignore the effects of any changes in the surface element, in terms of both area and orientation. Thus, the light variations expressed at the stellar surface may be written as 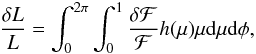 (1)where μ = cosθ and h(μ) is the so-called normalized limb darkening function (e.g. Mihalas 1978).
(1)where μ = cosθ and h(μ) is the so-called normalized limb darkening function (e.g. Mihalas 1978).
The fluctuation δℱ is the unknown quantity that remains to be determined. In roAp stars, the modes are strongly influenced by both magnetic and inertial forces. The joint effect produced by these two perturbations is non-spherically symmetric, leading to a distortion of the surface amplitude of the modes. Mathematically, this means that δℱ is written as a linear combination involving spherical harmonics of different degrees ℓ and corresponding azimuthal orders m = [ − ℓ,ℓ] . The eigenmodes are solutions of an eigenvalue system. The eigenvalues are the frequencies, and the eigenvectors are the coefficients of the spherical harmonic expansion.
In this context, Kurtz (1992) proposed that the light variations of roAp stars could be interpreted in terms of axisymmetric modes (m = 0) about the magnetic field, whose angular dependence is described by a linear combination of ℓ ( = 0,1,2,3). This combination of spherical harmonics was used to take into account the distortion produced by the magnetic field. Dziembowski & Goode (1996) and Bigot et al. (2000) showed in the case of dipole magnetic fields that the distortion of the eigenvectors is quite weak as long as the field strength remains < 1 kG and can be regarded as a small correction to the problem. Cunha & Gough (2000), Saio & Gautschy (2004), Saio (2005), and Cunha (2006) explored the effects of stronger fields and showed that the surface amplitudes of the modes are strongly modified by kilogauss field strengths as found in roAp stars. However, photometric observations show dominant triplets, which mean that either the magnetic distortion is small or the geometric cancellation (integration over the stellar disk) of components ℓ > 1 leads the observer to see the distorted mode as a dipole. In the following, we assume a negligible magnetic distortion in order to develop an analytical formalism, keeping in mind that it might not be applicable to all roAp stars.
In this respect, the perturbation of the radiative flux may be written as ![\begin{equation} \label{eq:deltaf} \frac{\delta {\cal F}}{{\cal F}} (\mu_R,\phi_R,t) =\epsilon {\it f}_{\ell}\left [\sum_{m=-\ell}^{\ell} a_m Y_{\ell}^m(\mu_R,\phi_R)\right ] {\rm e}^{{\rm i }\omega t}, \end{equation}](/articles/aa/full_html/2011/12/aa16981-11/aa16981-11-eq21.png) (2)where am are the coefficients of the coupling and ω the frequency. These quantities are, respectively, the eigenvectors and eigenvalues of an homogenous system (e.g. Dziembowski & Goode 1985; Kurtz & Shibahashi 1986; Bigot & Dziembowski 2002). They depend on the magnetic and rotation strengths and orientations. The quantity fℓ is a function that characterizes the radial dependence of δℱ and is expressed here at the stellar surface. The coefficient ϵ is unknown in the linear treatment of the oscillations, but is a small parameter so the perturbation formalism is valid. The
(2)where am are the coefficients of the coupling and ω the frequency. These quantities are, respectively, the eigenvectors and eigenvalues of an homogenous system (e.g. Dziembowski & Goode 1985; Kurtz & Shibahashi 1986; Bigot & Dziembowski 2002). They depend on the magnetic and rotation strengths and orientations. The quantity fℓ is a function that characterizes the radial dependence of δℱ and is expressed here at the stellar surface. The coefficient ϵ is unknown in the linear treatment of the oscillations, but is a small parameter so the perturbation formalism is valid. The 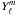 are the usual spherical harmonics expressed in the rotation reference system, i.e. μR = 1 corresponds to the rotation axis.
are the usual spherical harmonics expressed in the rotation reference system, i.e. μR = 1 corresponds to the rotation axis.
We emphasize that the present approach differs from that of Kurtz (1992) since we consider that the distortion of the mode is described by a linear combination, not for ℓ, but for the azimuthal order m. We stress that because of the inclination between the magnetic and rotational perturbations the coupling of modes for different azimuthal orders m can be strong and cannot be ignored in roAp stars.
To proceed further and compare with observations, we have to write the flux variations described by Eq. (2) in the inertial reference system whose polar axis coincides with the line-of-sight of the observer. This operation is done via the well-known relation for spherical harmonics 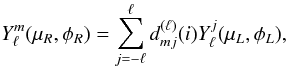 (3)where (μL,φL) are the coordinates in the new (observer’s) reference system, i the angle between the rotation axis and the line-of-sight, and
(3)where (μL,φL) are the coordinates in the new (observer’s) reference system, i the angle between the rotation axis and the line-of-sight, and 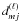 coefficients that are expressed in terms of the Jacobi polynomials (e.g. Edmonds 1960). Moreover, the observer being in an inertial frame, we have to transform the coordinate system as φR → φR − Ωt, where Ω is the rotation frequency of the star. Therefore, after substituting Eq. (3) into Eq. (2), and integrating over the stellar disk (only j = 0 remains in Eq. (3)) the expression for the fluctuation in luminosity is given by
coefficients that are expressed in terms of the Jacobi polynomials (e.g. Edmonds 1960). Moreover, the observer being in an inertial frame, we have to transform the coordinate system as φR → φR − Ωt, where Ω is the rotation frequency of the star. Therefore, after substituting Eq. (3) into Eq. (2), and integrating over the stellar disk (only j = 0 remains in Eq. (3)) the expression for the fluctuation in luminosity is given by 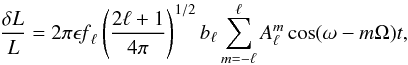 (4)where
(4)where ![\begin{equation} A_{\ell}^m =\left [\frac{(\ell-m)!}{(\ell+m)!}\right ]^{1/2} P_{\ell}^m (\cos i)\,\,a_m, \end{equation}](/articles/aa/full_html/2011/12/aa16981-11/aa16981-11-eq37.png) (5)and
(5)and 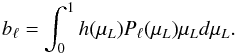 (6)Since we work at a given value of ℓ and consider only relative fluctuations in the following sections, we are not interested in the value of the constant in front of the sum in Eq. (4), and just consider
(6)Since we work at a given value of ℓ and consider only relative fluctuations in the following sections, we are not interested in the value of the constant in front of the sum in Eq. (4), and just consider 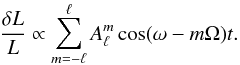 (7)This expression clearly shows the double modulation observed in roAp stars, a rapid one of period 2π/ω due to the oscillation and a long one of period 2π/Ω due to the rotation of the star. In the frequency domain, it leads to a (2ℓ + 1) multiplet of amplitudes Am equally spaced by the frequency of rotation.
(7)This expression clearly shows the double modulation observed in roAp stars, a rapid one of period 2π/ω due to the oscillation and a long one of period 2π/Ω due to the rotation of the star. In the frequency domain, it leads to a (2ℓ + 1) multiplet of amplitudes Am equally spaced by the frequency of rotation.
2.2. Light curve variations of dipole modes
The dipole modes have the most common geometry observed in photometry in roAp stars. They are therefore of special interest to asteroseismic studies. In the rest of this work, we will consider the fluctuations of luminosity in Eq. (7) for generalized dipole (ℓ = 1) modes, following the formalism developed in Bigot & Dziembowski (2002). We will present an analytical formulation of the light curves for both amplitudes and phases.
 |
Fig. 1 The oblique pulsator model for dipole modes (Bigot & Dziembowski 2002). During the pulsation cycle, the axis of the dipole mode lies in a fixed plane that is inclined to both the rotation and magnetic axes. The shape of the displacement vector is elliptical. The two axes of the ellipse are the X-axis in the (B,Ω) plane and the perpendicular y-axis. The x-axis lies in the rotation equatorial plane. The line-of-sight of the observer makes an angle α(t) with the former, and σ(t) with the latter. The magnetic axis is inclined by the angle λ(t) to the line-of-sight. |
2.2.1. Properties of dipole modes
As shown in Bigot & Dziembowski (2002), the dipole mode axis lies in a fixed plane during the pulsation cycle with an elliptical displacement vector.
The orientation and shape of the ellipse are defined by its two axes: the X-axis in the plane defined by the vectors (B,Ω) and the perpendicular y-axis. The inclination of the X-axis of the ellipse with respect to the rotation axis is given by ![\begin{equation} \gamma =\arctan\left [\frac{a_{+1}-a_{-1}}{\sqrt{2}a_0}\right ]\cdot \end{equation}](/articles/aa/full_html/2011/12/aa16981-11/aa16981-11-eq52.png) (8)The elliptical displacement of the mode is characterized by the polarization angle
(8)The elliptical displacement of the mode is characterized by the polarization angle ![\begin{equation} \psi=\arctan\left [\frac{a_{+1}+a_{-1}}{a_{+1}-a_{-1}}\sin\gamma\right ], \end{equation}](/articles/aa/full_html/2011/12/aa16981-11/aa16981-11-eq53.png) (9)which measures the ratio of the two axes of the ellipse. The projected amplitudes of the displacement vector onto the X- and y-axes are then cosψ and sinψ, respectively. We note that ψ = 0 corresponds to a mode that is linearly polarized in the plane (B,Ω), whereas ψ = ± π/2 corresponds to a mode that is linearly polarized along the y-axis.
(9)which measures the ratio of the two axes of the ellipse. The projected amplitudes of the displacement vector onto the X- and y-axes are then cosψ and sinψ, respectively. We note that ψ = 0 corresponds to a mode that is linearly polarized in the plane (B,Ω), whereas ψ = ± π/2 corresponds to a mode that is linearly polarized along the y-axis.
The special cases are:
-
(|γ| = 0,ψ = 0) for a mode linearly polarized along the rotation axis, i.e. an mR = 0 mode in the rotation system;
-
(|γ| = π/2,ψ = ± π/4) for a mode circularly polarized in a plane orthogonal to the rotation axis, i.e. an mR = ± 1 mode in the rotation system;
-
(|γ| = β,ψ = 0) for a mode linearly polarized along the magnetic axis, i.e. an mB = 0 mode in the magnetic system;
-
(|γ| = π/2 − β,ψ = ± π/4) for a mode circularly polarized in a plane orthogonal to the magnetic axis, i.e. an mB = ± 1 mode in the magnetic system.
2.2.2. Amplitudes and phases of the light curves
The light curve associated with a dipole mode may be obtained from Eq. (7) with ℓ = 1. We write it in a form similar to that in Kurtz (1992) 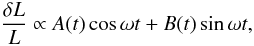 (10)but with different coefficients A(t) and B(t),
(10)but with different coefficients A(t) and B(t), 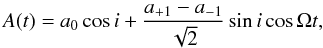 (11)and
(11)and 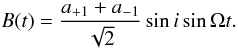 (12)These expressions can be written in terms of γ and ψ as
(12)These expressions can be written in terms of γ and ψ as 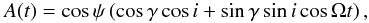 (13)and
(13)and 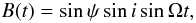 (14)where we have normalized each coefficient am (which are solutions for a homogeneous system) by
(14)where we have normalized each coefficient am (which are solutions for a homogeneous system) by 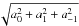 .
.
From the observer’s point of view, the relevant quantities are the orientations of the X- and y-axes with respect to the line-of-sight, rather than the orientation with respect to the rotation axis (z-axis). It is then more natural to consider the angles made by these two axes to the line-of-sight instead of the angles γ and i.
To define these angles, we consider the three directions of the problem that are defined by the three following unit vectors:
The angle α(t) between the X-axis of the ellipse and the line-of-sight is then defined by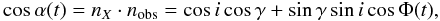 (18)and the angle σ(t) between the y-axis of the ellipse and the line-of-sight is
(18)and the angle σ(t) between the y-axis of the ellipse and the line-of-sight is 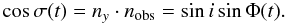 (19)The expressions for the coefficients A(t) and B(t) reduce to simple forms
(19)The expressions for the coefficients A(t) and B(t) reduce to simple forms  These quantities then have a simple physical explanation: they correspond to the lengths of the X- and y-axes of the ellipse (cosψ and sinψ, respectively, in the mode plane) projected onto the line-of-sight. The amplitude and phase of the signal related to the dipole modes are finally only functions of three quantities: the eccentricity of the ellipse (ψ) and its orientation with respect to the observer (α, σ).
These quantities then have a simple physical explanation: they correspond to the lengths of the X- and y-axes of the ellipse (cosψ and sinψ, respectively, in the mode plane) projected onto the line-of-sight. The amplitude and phase of the signal related to the dipole modes are finally only functions of three quantities: the eccentricity of the ellipse (ψ) and its orientation with respect to the observer (α, σ).
Following Kurtz (1992), we write the light curve in terms of its amplitude R(t) and phase Ψ(t) 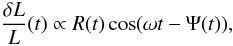 (22)with
(22)with 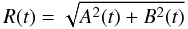 (23)and
(23)and ![\begin{equation} \label{eq:pha} \Psi(t) = \arctan\left [\frac{B(t)}{A(t)}\right ]\cdot \end{equation}](/articles/aa/full_html/2011/12/aa16981-11/aa16981-11-eq90.png) (24)The behaviour of the amplitude R and phase Ψ for different mode inclinations and polarizations is represented in Fig. 2.
(24)The behaviour of the amplitude R and phase Ψ for different mode inclinations and polarizations is represented in Fig. 2.
 |
Fig. 2 Shapes of the light curves influenced by different inclinations and polarizations of the dipole mode. In both panels, the inclination of the observer is i = 70°. (Left panel) We consider a given polarization of the mode ψ = 5°, and compute curves for various inclinations of the mode plane: γ = 5° (—), 25° (···), 45° (− − −), 65° (−·−), 85° (−···−). It is clear that for all inclinations but one (γ = 5°), the phase jumps π radians exactly at the amplitude minima since the modes show the two hemispheres during the rotation period (i.e., this verifies the conditions given in Eq. (A.2)). The position of the minima at Φm are shifted by a change in the inclination of the mode, as one can check in Eq. (25). (Right panel) Shapes of the light curves influenced by different polarizations of the dipole mode. We consider a given inclination of the mode γ = 45°, and compute curves for various polarizations ψ of the dipole axis: ψ = 0° (—), 20° (···), 40° (− − −), 60° (−·−), 80° (−···−). In both panels, we have represented two periods of rotation. |
3. Extrema of the rotationally-modulated amplitudes of dipole modes and their coincidence with magnetic maxima
The number and nature of the extrema of the rotationally-modulated amplitudes depend on the aspect of the dipole mode seen by the observer. In general, within one period of rotation, Φ = [0,2π] , we count four extrema located at ![\begin{equation} \label{eq:extrema} \Phi =0\,[\pi] \hspace{.4cm}{\rm and} \hspace{.4cm}\Phi\equiv \Phi_{\rm o}^{\pm} =\pm\arccos\left (\frac{\xi}{\tau^2 -1}\right ), \end{equation}](/articles/aa/full_html/2011/12/aa16981-11/aa16981-11-eq110.png) (25)where τ = tanψ/sinγ and ξ = cotγcoti. The presence of four extrema of the envelope, despite the dipolar nature of the mode, is a direct consequence of the definition of R(Φ) introduced in Eq. (23).
(25)where τ = tanψ/sinγ and ξ = cotγcoti. The presence of four extrema of the envelope, despite the dipolar nature of the mode, is a direct consequence of the definition of R(Φ) introduced in Eq. (23).
In some special cases (polarization and/or inclination), the observer might see only two extrema. This may occur for example if |ξ| ≥ |τ2 − 1|. In that case, the observer sees extrema only at Φ = 0 [π] . The inclination of the observer relatively to the mode axis is such that the same hemisphere is always seen as the star rotates. An illustration is given in the appendix in the special case of ψ = 0 modes.
Another case for the presence of only two extrema is found when the displacement vector of the mode is always perpendicular to the (B,Ω) plane, i.e. when |ψ| = π/2. In that case, there are no extrema at Φ = 0 [π] , but only at Φ = Φo = ± π/2.
In the following, we focus our discussion of the extrema located at Φ = 0 [π] . The objective is to determine under which conditions the pulsations show maxima in phase with the magnetic maxima.
3.1. The extrema of the magnetic field
Owing to its inclination with respect to the rotation axis, the magnetic field is also modulated as the star rotates. The modulation depends on the orientation of its axis with respect to the line-of-sight of the observer. This describes the standard, well-known oblique rotator model (Stibbs 1950). Here we present this model in our notation.
The direction of the magnetic field axis with the rotation axis is defined by the unit vector 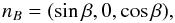 (26)where β is the angle between the two axes. From the observer’s line-of-sight, the magnetic axis is inclined by an angle λ defined by
(26)where β is the angle between the two axes. From the observer’s line-of-sight, the magnetic axis is inclined by an angle λ defined by 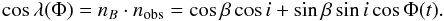 (27)Hence, the magnetic modulation due to the rotation of the star is
(27)Hence, the magnetic modulation due to the rotation of the star is 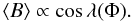 (28)This magnetic variation is a sinusoid with two maxima at Φ = 0 and Φ = π. These maxima can be positive or negative depending on the value of λ at Φ = 0 or Φ = π.
(28)This magnetic variation is a sinusoid with two maxima at Φ = 0 and Φ = π. These maxima can be positive or negative depending on the value of λ at Φ = 0 or Φ = π.
The condition that has to be met for a positive maximum at Φ = 0 and a negative minimum at Φ = π is 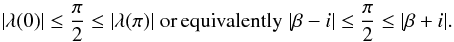 (29)The first inequality ensures that there is a positive maximum at Φ = 0, i.e.
(29)The first inequality ensures that there is a positive maximum at Φ = 0, i.e. 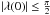 , and the second one ensures that there is a second negative maximum, i.e.
, and the second one ensures that there is a second negative maximum, i.e. 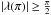 .
.
3.2. The extrema of pulsation at Φ = 0 [π]
We now consider the nature of the pulsation extrema at the same rotation phases as those of the magnetic extrema. The first requirement to have magnetic and pulsation maxima in phase is obviously that the rotational envelope shows extrema at Φ = 0 [π] . This means that the mode must have a non-zero amplitude in the magnetic plane (B,Ω), which requires that |ψ| ≠ π/2 [π] . If this condition is satisfied, the dipole mode always has two extrema in phase with the magnetic extrema at Φ = 0 [π] , since the X-axis of the ellipse is within the magnetic plane. The question is then to know whether these extrema are maxima or minima. The answer depends on both the polarization ψ of the dipole mode and its orientation toward the observer.
At the rotation phase Φ = 0 [π] , the angles between the X-axis of the ellipse and the line-of-sight are 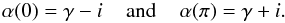 (30)The y-axis of the ellipse is perpendicular to the line-of-sight (σ = ± π/2) so its projected component becomes zero. The condition under which R(Φ) shows a maximum at Φ = 0 is easily derived by a simple analysis of Eq. (23). We find that
(30)The y-axis of the ellipse is perpendicular to the line-of-sight (σ = ± π/2) so its projected component becomes zero. The condition under which R(Φ) shows a maximum at Φ = 0 is easily derived by a simple analysis of Eq. (23). We find that 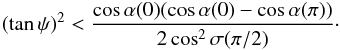 (31)A similar expression is obtained at the phase Φ = π,
(31)A similar expression is obtained at the phase Φ = π, 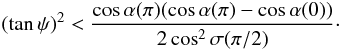 (32)The conditions Eqs. (31) and (32) are restrictive, in the sense that for a given position of the observer relative to the mode axis (i.e. X-axis at Φ = 0 [π]), there is upper limit to the strength of the polarization allowed. In other words, the displacement vector has to stay close to the (B,Ω) plane in order to show a maximum in phase with the magnetic one.
(32)The conditions Eqs. (31) and (32) are restrictive, in the sense that for a given position of the observer relative to the mode axis (i.e. X-axis at Φ = 0 [π]), there is upper limit to the strength of the polarization allowed. In other words, the displacement vector has to stay close to the (B,Ω) plane in order to show a maximum in phase with the magnetic one.
 |
Fig. 3 Representation of the rotational variation of the light curves in amplitude and phase for three dipole modes on the six rows, and for three regimes of magnetic field in the three columns, μ = −0.2, −1.0 , and −5.0, where μ measures the ratio of the magnetic to centrifugal shifts of the pulsation frequencies. The amplitudes are normalized so that the maximum is equal to unity. In all cases, we choose i = 70° and β = 12°. The ratio of the Coriolis to centrifugal shifts of frequencies is χ = 0.01. See the text for a description of the properties of the three dipole modes. The values (in degrees) of the inclination and polarization are given for each mode in the brackets (γ,ψ) above the panels. |
It is important to note that these relations put some constraints on the polarization of the dipole mode. However, they allow modes that are (well) inclined to the magnetic field and have maxima in phase with the magnetic ones. Until now, it has been common to assume that the coincidence between the pulsation and magnetic maxima implies that modes are linearly polarized along the magnetic axis, say ψ = 0 and γ = β. Even though this case does lead to such a coincidence, it is certainly not the only possibility. The relations in Eqs. (31) and (32) indeed do not exclude modes with circular polarizations, ψ = ± π/4, and even modes that are more elongated along the y-axis (π/4 ≤ |ψ| < π/2).
This result is not obvious: modes that have the largest amplitude of their displacement vector in a direction perpendicular to the magnetic plane (B,Ω), i.e. modes such as (|ψ| > π/4), can show some maxima in phase with the magnetic maxima. This apparent contradiction can be easily explained because the observer does not see the real amplitude of the displacement vector but rather the projection of the X- and y-axes of the ellipse onto the line-of-sight. What really matters is the amplitude of the projection of the X-axis relative to the amplitude of the projection of the y-axis. The mode shows a maximum in phase with the magnetic maximum if the projection of its displacement in the plane (B,Ω) is larger than the one perpendicular to this plane.
To illustrate this, we consider an example: a mode with ψ = 55°, γ = 50°, and i = 10°. This mode is more elongated along the y-axis than the X-axis, since sinψ > cosψ. The inequalities in equations Eqs. (31) and (32) are fulfilled, and the two extrema at Φ = 0 and Φ = π are maxima. The projection of the X-axis onto the line-of-sight is a(Φ = 0) = 0.43, whereas the projection of the y-axis is b(Φ = π/2) = 0.14. Hence, the mode shows a maximum at Φ = 0 because the projection of the displacement vector component in the plane (B,Ω) is larger than its component perpendicular to this plane (y-direction).
The two extrema have unequal amplitudes because the two poles of the mode have different inclinations (α(0) ≠ α(π)) with respect to the line-of- sight. The ratio of their amplitudes is given by 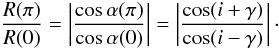 (33)This ratio is independent of ψ since at Φ = 0 [π] the small axis of the ellipse is perpendicular to the line-of-sight (null projection). We note that for some special values of the inclination of the observer, i = 0 [π/4] , this ratio equals one, regardless of the inclination of the mode. These cases are unfortunate for asteroseismology because they cannot provide information on the mode.
(33)This ratio is independent of ψ since at Φ = 0 [π] the small axis of the ellipse is perpendicular to the line-of-sight (null projection). We note that for some special values of the inclination of the observer, i = 0 [π/4] , this ratio equals one, regardless of the inclination of the mode. These cases are unfortunate for asteroseismology because they cannot provide information on the mode.
4. Magnetic versus rotation effects on the light curves
We now consider the influence of a varying magnetic field and rotation on the aspect of the light curves. At a given rotation frequency Ω, a change in the magnetic field strength modifies both the inclination and polarization of the mode, which thereby changes its aspect seen by the observer. The results on the combined effects of a magnetic field and rotation on the dipole mode property are discussed in detail in Bigot & Dziembowski (2002). To relate the present work to these results, we keep the same values for the mode parameters and the same notation as Bigot & Dziembowski (2002). The magnetic field strength is parameterized by the value of μ, which measures the ratio of the magnetic to centrifugal shifts in frequencies. We emphasize that no assumption is made regarding the method used to solve the magnetic shift of frequencies that enters into the μ parameter. The values of |μ| > 1 correspond to a predominant magnetic field regime, and |μ| < 1 corresponds to a regime where the centrifugal force dominates. In Fig. 3, we use μ = −0.2, −1.0 and −5.0. The ratio of Coriolis to centrifugal shifts of frequencies is kept to a constant value of 0.01, which is close to the real value corresponding to the roAp star HR 3831.
For dipole modes, the eigenvalue system leads to three orthogonal solutions that are represented on each row of Fig. 3. The aspect of these three modes is strongly modified when the magnetic field strength increases, as one can see from left to right:
-
1.
in the low magnetic field regime(|μ| < 1, left column), each eigenmode is almost described by a single spherical harmonic in the rotation system (mR = 0, ± 1). The mode that is almost an mR = 0 is not modulated because its axis nearly coincides with the rotation axis. The phase of the modes that are almost mR = ± 1 modes show this characteristic straight line variation for the phase;
-
2.
the most complicated situation arises when magnetic and rotation effects are comparable (|μ| = 1, middle column), where the coupling between m-components of the mode is the strongest. In that case, it is impossible to identify a mode with a single value of m;
-
3.
in the case of strong magnetic field (|μ| > 1, right column), the modes are again almost described by a single value of m but now in the magnetic reference system. The one that is almost described by an mB = 0 mode shows a constant phase except for phase reversals at amplitude minima. This jump corresponds to the moment when the node of the oscillations passes through the plane (i,Ω). The two other orthogonal modes are almost circularly polarized (ψ = ± π/4) and tend to show characteristic monotonic linearly increasing or decreasing phases.
For a given mode (a given row in Fig. 3), the light curve aspect changes drastically with the value of μ. This is because the mode tends to be aligned with (mB = 0), or orthogonal (|mB| = 1) to, the magnetic axis as the field strength increases. This changes both the numbers and the amplitudes of the maxima of the rotational envelope, as well as the polarization. The mode that is almost an |mR| = 1 mode in the rotation frame for μ < 1 becomes an mB = 0 mode in the magnetic frame when μ > 1. Its phase curve changes from nearly straight lines to constant phase with jumps.
We emphasize that there is a saturation effect once the magnetic field (equivalently μ) reaches a certain value (~4−5). Once the field is large enough, the three eigenmodes are either aligned or perpendicular to the magnetic axis and an increase in the field strength no longer has an effect on the aspect of the mode seen by the observer. Therefore, it becomes impossible to constrain the field strength above a certain limit by fitting the relative mode amplitudes. A tighter constraint is provided by the frequency spacing.
5. Applications to four roAp stars
5.1. Application to HR 3831
We apply these considerations to the roAp star HR 3831 for which we have good time measurements for both magnetic and pulsation data. This star pulsates in a single mode with a frequency of ω/2π = 1427 μHz (Kurtz et al. 1997a). From photometric data, the mode appears essentially as a dipole since there is a clear phase reversal of π at the minima of the rotational envelope. Equivalently, this appears in the frequency domain as a dominant triplet with peaks that are exactly separated by the rotation frequency, and is clear evidence of a dipole mode pulsation. Extra ℓ ≠ 1 components are present in the spectrum, which indicates a distortion of the dipole by the magnetic field (Kurtz et al. 1997a), but they appear small in photometry, possibly because of either a slight influence of the magnetic field or a geometrical cancellation (Saio & Gautschy 2004, Sect. 5.4) of the distorted mode.
The radial velocity measurements of Kochukhov (2006) indicate that the Nd iii lines have a strong ℓ = 3 component, much larger than in photometry, which is in strong disagreement with the mode geometry assumption of ℓ = 1 made in Sect. 2. We emphasize however that the Nd iii lines are formed very high in the atmosphere – τ5000 ≈ 10-4 − 10-5 – far above the continuum-forming region τ5000 ≈ 1 that we observe in photometry, hence the two sets of observations do not sample the same layers of the star. The Nd iii line formation is above the outer turning point of the mode reflection and therefore radial velocity measurements of this line do not correspond to the trapped magneto-acoustic modes but rather to the running part of mode in the atmosphere.
As mentioned in Sect. 2, our formalism is applicable to the modes that are weakly distorted by magnetic field such that they can be represented by a single value of ℓ = 1. We therefore assume that it is the case for HR 3831. Our formalism enables us to determine the mode inclination with respect to the rotation axis by comparing with observed light curves. One needs an independent determination of the magnetic field axis orientation to conclude about the alignment of the mode with magnetic axis.
The magnetic field of HR 3831 was first measured by Thompson (1981), who found a dipole field and determined the star’s magnetic ephemeris. These magnetic data and a large set of pulsation data were analysed by Kurtz et al. (1992), who found that the time of the magnetic minimum coincides with the time of the pulsation maximum. More precisely, the weakest of the two maxima of the rotational envelope of pulsation coincides with the positive extremum of the magnetic field variations.
 |
Fig. 4 Applications to four roAp stars: HR 3831 (upper left), HD 6532 (upper right), α Cir (lower left), and HD 99563 (lower right). The dots represent the observed values and the full lines the theory. Observational data are from Kurtz et al. (1997a) for HR 3831, Kurtz et al. (1996a) for HD 6532, Bruntt et al. (2009) for α Cir, and Handler et al. (2006) for HD 99563. In our linear treatment of pulsation, the absolute amplitude of the mode is arbitrary. Therefore, the amplitudes of the light curves are scaled so that the observed ones equal the theoretical ones at Φ = 0. The theoretical pulsation phase is with respect to an arbitrary zero-point in time, so is shifted to reproduce the observed pulsation phase at rotation phase Φ = 0. The best-fits to these curves are (i = 68°, γ = 91°, ψ = −7°) for HR 3831, (i = 40°, γ = 70°, ψ = −15°) for HD 6532 (i = 37°, γ = 20°, ψ = 0.5°) for α Cir, and (i = 44°, γ = 86°, ψ = −9°) for HD 99563. The different shapes of the amplitudes are caused by different inclinations of the mode axes with respect to the line-of-sight of the observer. The four modes are almost linearly polarized. The rotational variabilities of the magnetic fields of HD 6532, α Cir, and HD 99563 are not known; such observations will thus test our model for agreement with the angles we have given. |
More recent magnetic observations were carried by Mathys (1995), Bagnulo et al. (1999) and Kochukhov et al. (2004). They found drastically different results concerning both the polar magnetic strength (Bp) and orientation toward the rotation axis (β). In the first two papers, the values of the field strength are considerably stronger (Bp ~ 11 kG) than that of Kochukhov et al. (Bp ~ 2.5 kG). The orientations with respect to the rotation axis are also very different with β = 7° in Bagnulo et al. (1999) and 87° in Kochukhov et al. (2004). These differences are discussed in Kochukhov et al. (2004) who argued that these discrepancies are probably caused by the neglect of Mathys and Bagnulo et al. of the presence of stellar spots in their analysis.
We emphasize at this stage that the magnetic measurements of Bagnulo et al. (1999) appear incompatible with the presence of dipole-like pulsation aligned with the magnetic axis. That would indeed imply an improbably high pulsation amplitude that is not believable: the observed amplitude of the pulsation would be R(λ = 82°) = R(λ = 0°)cos(82). The observed semi- amplitude for HR 3831 is about 5 mmag in B; with this geometry, if the mode could be seen pole-on (λ = 0), then it would have an intrinsic semi- amplitude of 36 mmag! This is vastly larger than the largest amplitude seen for any of the known roAp star of 8 mmag, i.e. in the case of HD 60435, and that is for multiple modes beating with each other.
In their work, Bigot & Dziembowski (2002) determined the magnetic configuration (Bp,β,i) of the star by fitting the relative amplitudes of the triplet. With these parameters, they derived the mode inclination. However, this approach leads to two independent constraints, and the authors had to rely on an independent determination of the inclination to the line of sight i. At that time, this value was available in Bagnulo et al. (1999), who proposed that i = 89°. Using that value of i, Bigot & Dziembowski identified a mode that is almost linearly polarized along the X-axis (ψ is small) but with an axis of symmetry that is steeply inclined to the magnetic or rotation axes, 35° and 42°, respectively. This result was surprising because it suggested for the time that modes in roAp may not be aligned with the magnetic field axis. This result was questioned by Kochukhov (2006), who found a mode nearly that is aligned with the magnetic axis from radial velocity measurements. He argued that the geometrical model of Bigot & Dziembowski (2002) is too simple to account for the complexity of pulsation in these objects.
We however emphasize that the validity of the formalism in Bigot & Dziembowski (2002) cannot be questioned by this argument, the two studies not being based on the same observational constraints. A different value of i leads to a completely different value of the mode inclination. As a matter of fact, if we assume the value proposed by Kochukhov (2006), i.e. i = 68°, the geometrical model fits the light curve variations very well for both the amplitudes and phases, as seen in Fig. 4. The mode is now inclined by γ = 91° with respect to the rotation axis, i.e. almost aligned with the magnetic axis (if we assume the value of β = 87° given by Kochukhov et al. 2004). This mode is still found to be almost linearly polarized, i.e. with a small non-axisymmetric components, since |ψ| ≈ 7°. The ratio of magnetic to centrifugal shifts of frequencies is μ ≈ −0.8. As shown in Fig. 2 of Bigot & Dziembowski (2002), even if magnetic and centrifugal shifts are comparable (|μ| ≈ 1), the modes can be almost linearly polarized along the magnetic axis if β is large. At the time of the positive magnetic extrema, the angle of the pulsation axis with the line of sight is α(0) = 23° and half-rotation period later α(π) = 159°. These results are in good agreement with those presented in Kochukhov (2006).
Since the data of Bagnulo et al. (1999) are unlikely, we conclude that the pulsation mode in HR 3831 is nearly aligned with the magnetic axis.
5.2. Application to HD 6532
HD 6532 is one of the few roAp stars to show a polarity-reversing dipole-like pulsation mode (Kurtz et al. 1996a); the others are HR 3831 discussed in the last section, HD 99563 (Handler et al. 2006, and below), and HD 80316 (Kurtz at al. 1997b). The star HD 6532 has a short rotation period of only 1.944973 d (Kurtz et al. 1996b), hence a relatively rapid rotational velocity, similar to that of HR 3831. The geometry of the star is such that one pulsation pole is seen for about two-thirds of the rotation period, and the other for one-thirds, with a pulsation phase reversal at quadrature. With this geometry, one pole is seen at a far more favourable aspect than the other, hence at larger amplitude.
Little is known about the magnetic field of HD 6532. Mathys & Hubrig (1997) did not detect the longitudinal field, but found a significant quadratic field of 22 ± 4 G. Magnetic measurements are not easy to make for HD 6532, given its relative faintness (V = 8.4) and rotationally-broadened lines. We are thus unable to compare our pulsation solution to the light curves of HD 6532 with independent magnetic data, but we can make predictions about the geometry of the star that can be tested by future magnetic measurements.
We modelled the pulsation data for HD 6532 taken from Kurtz et al. (1996a). The best fit for we have obtained is (i = 40°, γ = 70°, ψ = −15°). The mode axis is closer to the line-of-sight than in HR 3831, i.e. α(0) = 30° and α(π) = 110°. The difference between the two maxima is therefore larger for this star than for HR 3831; we found that R(0)/R(π) ≈ 2.5, as seen in Fig. 4. With these values of α, the observer sees the two hemispheres as the star rotates, as in HR 3831. The important point here is that we can match the rotational amplitude and phase variations seen in the light curves of HD 6532 with our model and make clear predictions about the geometry that can be tested against future magnetic measurements.
5.3. Application to α Cir
The star α Cir is the brightest of the roAp stars (V = 3.2) and has basically a single pulsation mode with a frequency of 2.442 mHz (P = 6.8 min) (Kurtz et al. 1994; Bruntt et al. 2009). Several other modes of consecutive odd-even degrees are present but with smaller amplitudes (Bruntt et al. 2009). These authors derived a larger value of the large separation Δν = 60 μHz than the previous estimate (Kurtz et al. 1994). This new value of Δν, combined with a drastic downward revision of the effective temperature (7400 K) thanks to an interferometric radius determination (Bruntt et al. 2008), leads for the first time to consistent asteroseismic and Hipparcos parallaxes, in contrast to the result found by Matthews et al. (1999). There had been a long history of attempts to find the rotation period of α Cir until it was finally determined by an analysis of the pulsation data; the rotation period is 4.4790 ± 0.0001 d (Bruntt et al. 2009). The rotational sidelobes in the amplitude spectrum for this star are small, indicating that there is little modulation of the amplitude, hence this aspect of the pulsation mode does not vary much with rotation.
That is also true for the magnetic field, for which no rotational variations have therefore been detected. Mathys & Hubrig (1997) detected no longitudinal field, but found a quadratic field strength of 7.5 kG. As for HD 6532 above, we cannot test our model against independent magnetic measurements, but the geometry that we find can be tested against future, higher precision magnetic measurements.
We modelled pulsation data for α Cir taken from Bruntt et al. (2009); these are white light data taken by the WIRE satellite that have a higher precision than the B data of Kurtz et al. (1994), but otherwise have the same rotational modulation. We used the value of i = 37° found by Bruntt et al. (2008) by combining an interferometric determination of the radius with the determination of vsini by line spectroscopy. Our best-fit is (γ = 20°, ψ = 0.5°). In this case, the mode axis is still almost linearly polarized along the rotation axis (γ = 20°). The angles made by the pulsation axis to the line-of-sight, at the time of the two maxima, are close, i.e. α(0) = 17° and α(π) = 57°. Owing to the small tilt of the pulsation axis with respect to the rotation one, the observer always sees the same hemisphere and there is no phase reversal. The phase is therefore nearly constant. The ellipticity ψ is very small for this star with a value of 0.5°. This mode is very close to an mR = 0 mode.
5.4. Application to HD 99563
The star HD 99563 is a singly-periodic roAp star pulsating in a distorted dipole mode that shows both pulsation poles over the rotational cycle. Photometrically, it is one of the larger amplitude roAp stars with a semi-amplitude as high as 6 mmag in Johnson B (Handler et al. 2006). Its radial velocity variations have the highest amplitudes seen for an roAp star, reaching 5 km s-1 for some Eu ii lines, as a consequence of their strong concentration in small abundance spots near the pulsation poles (Freyhammer et al. 2009), their stratification high in the atmosphere, and the intrinsically high pulsation amplitude of HD 99563 (for an roAp star). The rotation period for HD 99563 was determined by Handler et al. (2006) to be Prot = 2.91179 ± 0.00007 d. Some variation in both the amplitude and phase with rotation, plus the strong ℓ = 3 components found by Handler et al. show this star to have a magnetically distorted dipole mode. Freyhammer et al. (2009) showed that some rare earth elements are overabundant by more than 106 solar values in spots, and that even H shows a nonuniform surface distribution as a consequence of the rare-earth element patches. The result of this is that the observations – even in photometry – do not sample the surface uniformly. The spatial filter caused by the extreme abundance anomalies is probably the source of the apparent distortion of the mode determined from photometry.
We modeled the multisite photometric observations of Handler et al. (2006) using the rotational inclination i = 44° determined by those authors. From this, we found that γ = 86° and ψ = −9°, as can be seen in Fig. 4. This is the poorest fit of our model to the four stars tested, which we believe is a result of the strong distortion of the observations by the surface spatial filter. An interesting test of this would be to study the pulsation of HD 99563 in Johnson V, where there is little rotational variation in the mean light (see Fig. 4 of Handler et al. 2006). While the pulsation amplitude will be smaller in Johnson V than B, the star is of sufficiently high amplitude to ensure that data of good signal- to-noise ratio can be obtained. We expect that such observations will show a weaker distortion. Magnetic measurements of HD 99563 are consistent with the pulsation geometry (see Freyhammer et al. 2009, for a discussion). As for HR 3831, the mode axis is nearly aligned with the magnetic one (β = 88°, see Freyhammer et al. 2009).
5.5. Comparison of the four roAp stars
On the basis of this small sample, it appears that there is no preferential inclination of the pulsation axis to the rotation one since γ = 91°, 70°, 20°, and 86°. The lack of magnetic data prevent any general conclusion regarding the alignment of the mode and magnetic axes. However, for the two roAp stars (HR 3831, HD 99563) for which we have the value of magnetic obliquity β, we found from the light curve analysis that the modes are nearly aligned with the magnetic axis (γ ≈ β). The different behaviour of the light curves is explained by the different inclinations of their axis of symmetry to the line-of-sight. We note, however, that there is a tendency for the modes to have small ellipticities of |ψ| = 7°, 15°, 0.5°, and 9°. A new polarity-reversing roAp star found by the Kepler mission, KIC 101095926 shows a similar small ellipticity of |ψ| = 4° (Kurtz et al. 2011). This means that most of the displacement vectors of these modes remain very close to the magnetic plane during the pulsation cycle. This may be a common property of roAp stars that should be investigated by considering a much larger sample than the present one.
6. Conclusions
We have presented a formalism to explain the aspect of the light curves associated with dipole oscillations in roAp stars. In this purely geometrical model, all the complexity is reduced to three aspect angles, namely the mode and observer inclinations with respect to the rotation axis and the polarization angle of the mode. This geometrical model can reproduce global mode properties and is particularly useful for asteroseismic diagnostics. As we have shown, the model works well with the four roAp stars considered in this paper. Owing to its simplicity, it has limitations and cannot reproduce detailed line profile variation or derived accurate field strength. This would need a more realistic rotation-magneto- hydrodynamic numerical model.
We have shown that the light curve variations in roAp stars are strongly influenced by the magnetic field strength, which is parameterized in this study by a single parameter. The reason is that an increase in the field strength pushes the mode to be either aligned or perpendicular to the magnetic axis. This consequently changes the aspect of the projection of the mode onto the line-of-sight of the observer. We have also clearly shown that the coincidence between the observed pulsation and magnetic maxima is not evidence of an alignment of their respective axes as had been commonly thought.
We have applied this formalism to four roAp stars and in particular the well-studied roAp star HR 3831. For this star, we revised the conclusion of Bigot & Dziembowski (2002), who derived a highly inclined dipole mode with respect to the magnetic axis. We do not question their formalism, but rather the magnetic data they used. Indeed, in either the light curve or triplet analysis, one needs to assume an inclination for the observer. The one used by Bigot & Dziembowski (2002) was taken from Bagnulo et al. (1999) and led to well inclined mode. Using the more recent and the more reliable data of Kochukhov (2006), we have found a mode that is nearly aligned with the magnetic axis, quite close to the original picture of the oblique pulsator model of Kurtz (1982). This means that the magnetic field strength is strong ( ≥ 1 kG). In this respect, the value of 2.5 kG proposed by Kochukhov et al. (2004) agrees with the present conclusions. This strength makes the centrifugal force inefficient to tilt significantly the mode axis far from the magnetic axis.
The geometrical picture of pulsation presented in Bigot & Dziembowski (2002) and in this paper clearly explains the photometric data and leads to mode properties that are in good agreement with radial velocity measurements, at least in the case of HR 3831. In this model, the inclination γ and polarization ψ are two global properties of the standing mode and therefore do not vary with depth. This is the converse of the result that Kochukhov (2006) found for radial velocity measurements of Pr and Nd lines. He claimed that the geometrical approach is inadequate since it does not account for this variation with depth. We, however, emphasize that the variation in the ratio of the peak amplitudes of the triplet found by Kochukhov (equivalently γ and ψ) indicates the presence of a running wave travelling in the atmosphere far above the continuum-forming region where the fluctuations of luminosity originate. As shown by Saio et al. (2010) with a realistic magneto-hydrodynamic pulsation model, the phase of the standing mode is constant in the deep atmosphere and in the interior, whereas the running wave in the atmosphere has a changing phase with depth. Our formalism applies to the global standing mode whose phase is therefore constant, and the parameters γ and ψ can be regarded as global geometrical parameters.
Acknowledgments
L.B. thanks W. Dziembowski for fruitful discussions at an early stage of this work and the referee, H. Saio, for his constructive suggestions.
References
- Bagnulo, S., Landolfi, M., & degl’Innocenti, M. L. 1999, A&A, 343, 865 [NASA ADS] [Google Scholar]
- Bigot, L., & Dziembowski, W. A. 2002, A&A, 391, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bigot, L., Provost, J., Berthomieu, G., Dziembowski, W. A., & Goode, P. R. 2000, A&A, 356, 218 [NASA ADS] [Google Scholar]
- Bruntt, H., North, J. R., Cunha, M., et al. 2008, MNRAS, 386, 2039 [NASA ADS] [CrossRef] [Google Scholar]
- Bruntt, H., Kurtz, D. W., Cunha, M. S., et al. 2009, MNRAS, 396, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R. J., & Smith, M. A. 1979, ApJ, 232, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, M. S. 2006, MNRAS, 365, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, M. S., & Gough, D. 2000, MNRAS, 319, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W. A. 1977, AcA, 27, 203 [Google Scholar]
- Dziembowski, W. A., & Goode, P. R. 1985, ApJ, 296, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W. A., & Goode, P. R. 1996, ApJ, 458, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Edmonds, A. R. 1960, Angular Momentum in Quantum Mechanics, second edition (Princeton Univ. Press) [Google Scholar]
- Freyhammer, L. M., Kurtz, D. W., Elkin, V. G., et al. 2009, MNRAS, 396, 32 [Google Scholar]
- Handler, G., Weiss, W. W., Shobbrook, R. R., et al. 2006, MNRAS, 366, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Kochukhov, O. 2006, A&A, 446, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kochukhov, O., Drake, N. A., Piskunov, N., & de la Reza, R. 2004, A&A, 424, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurtz, D. W. 1978, Inf. Bull. Var. Stars, 1436 [Google Scholar]
- Kurtz, D. W. 1982, MNRAS, 200, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W. 1992, MNRAS, 259, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., & Shibahashi, H. 1986, MNRAS, 223, 557 [NASA ADS] [Google Scholar]
- Kurtz, D. W., Kanaan, A., Martinez, P., & Tripe, P. 1992, MNRAS, 255, 289 [NASA ADS] [Google Scholar]
- Kurtz, D. W., Sullivan, D. J., Martinez, P., & Tripe, P. 1994, MNRAS, 270, 674 [NASA ADS] [Google Scholar]
- Kurtz, D. W., Martinez, P., Koen, C., & Sullivan, D. J. 1996a, MNRAS, 281, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Marang, F., van Wyk, F., & Roberts, G. 1996b, MNRAS, 280, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., van Wyk, F., Roberts, G., et al. 1997a, MNRAS, 287, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Martinez, P., Tripe, P., & Hanbury, A. G. 1997b, MNRAS, 289, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Elkin, V. G., Cunha, M. S., et al. 2006, MNRAS, 372, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Cunha, M. S., Saio, H., et al. 2011, MNRAS, 414, 2550 [NASA ADS] [CrossRef] [Google Scholar]
- Landstreet, J. D., & Mathys, G. 2000, A&A, 359, 213 [NASA ADS] [Google Scholar]
- Mathys, G. 1995, A&A, 293, 746 [NASA ADS] [Google Scholar]
- Mathys, G., & Hubrig, S. 1997, A&AS, 124, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthews, J. M., Kurtz, D. W., & Martinez, P. 1999, ApJ, 511, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D. 1978, Stellar Atmospheres, second edition (San Francisco: Freeman) [Google Scholar]
- Saio, H. 2005, MNRAS, 360, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., & Gautschy, A. 2004, MNRAS, 350, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., Ryabchikova, T., & Sachkov, M. 2010, MNRAS, 403, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Shibahashi, H., & Takata, M. 1993, PASJ, 45, 617 [NASA ADS] [Google Scholar]
- Stibbs, D. W. N. 1950, MNRAS, 110, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Takata, M., & Shibahashi, H. 1995, PASJ, 47, 219 [NASA ADS] [Google Scholar]
- Thompson, I. B. 1983, MNRAS, 205, 43 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Special types of light curves
 |
Fig. A.1 Representation of the light curves for linear polarized (ψ = 0) dipole modes with different inclinations of the pulsation axis. This illustrates the cases discussed in Sect. A.0.1. In both figures, the position of the observer is fixed, i = 40°. Left panel: the dipole axis remains close to the line-of-sight during the rotation of the star. The observer only sees one hemisphere of the mode, and thereby does not observe a phase jump during the rotation period. Hence, a maximum and minimum of the rotational envelope of the pulsation are observed at Φ = 0 and Φ = π. Right panel: the dipole axis is now sufficiently inclined with respect to the line-of-sight so that the two hemispheres of the dipole can been seen by the observer. A phase jump by π radians occurs when the node of the oscillations crosses the plane (i,Ω). In this case, the amplitude of the rotational envelope leads to two maxima of different amplitudes (α(0) < α(π)). |
We apply the general formalism developed in this paper to special values of the polarization given by ψ = 0, |ψ| = π/2, and |ψ| = π/4.
A.0.1. Linear polarization ψ = 0
We consider the important case of modes linearly polarized in the plane (B,Ω), characterized by a value of ψ = 0. This case, which is even idealistic, is not far from reality since it is believed that most of the pulsation modes in roAp stars are almost linearly polarized.
These dipole modes (ψ = 0) always show extrema in phase with the magnetic extrema because their pulsation axes lie in the plane (B,Ω). Their amplitude is written 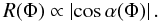 (A.1)To precisely examine the coincidence between magnetic and pulsation maxima, we have to consider four angles which are the angles between the mode axis and the line-of-sight at the two extrema, α(Φ = 0) and α(Φ = π), and the angle between the magnetic axis and the line-of-sight at the same phases, λ(Φ = 0) and λ(Φ = π).
(A.1)To precisely examine the coincidence between magnetic and pulsation maxima, we have to consider four angles which are the angles between the mode axis and the line-of-sight at the two extrema, α(Φ = 0) and α(Φ = π), and the angle between the magnetic axis and the line-of-sight at the same phases, λ(Φ = 0) and λ(Φ = π).
The conditions required to have maxima at Φ = 0 [π] , i.e. Eqs. (31), (32), can be divided into the following three cases:
-
Case I: the mode shows two maxima atΦ = 0 and Φ = π, with phases Ψ of opposite signs:
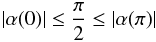 (A.2)or
(A.2)or 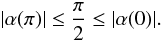 (A.3)In this case, the observer sees the two hemispheres of the dipole as the star rotates. The light curves resemble those shown in Fig. A.1.
(A.3)In this case, the observer sees the two hemispheres of the dipole as the star rotates. The light curves resemble those shown in Fig. A.1. Case II: the mode shows one maximum at Φ = 0 and a minimum at Φ = π, with the same signs for phases Ψ:
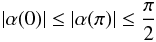 (A.4)or
(A.4)or 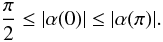 (A.5)
(A.5)-
Case III: the mode shows one maximum at Φ = π and a minimum at Φ = 0, with the same signs for the phases Ψ:
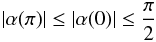 (A.6)or
(A.6)or 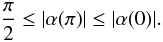 (A.7)
(A.7)
We also note that for some specific inclinations of either the rotation axis or the mode axis, the light curve shows some extrema of the same amplitude. In the case of i = 0 [π/4] and/or γ = 0 [π/2] , we have |α(0)| = |α(π)|, and thereby R(0) = R(π).
The coincidence between the magnetic and pulsation maxima can occur in many cases depending on the mode and the magnetic field orientation. For example, the condition to have pulsation maxima at Φ = 0 and at Φ = π and a magnetic positive maximum at Φ = 0 together with a negative magnetic minimum at Φ = π combines the relations Eqs. (A.2) and (29), which can be written 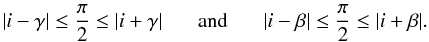 (A.8)This relation is not very restrictive and allows a wide range of values of (i,γ,β).
(A.8)This relation is not very restrictive and allows a wide range of values of (i,γ,β).
A.0.2. Linear polarization |ψ| = π/2
In the case of linearly polarized modes orthogonal to the plane (B,Ω), i.e. with |ψ| = π/2, we have 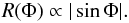 (A.9)No possible coincidence between magnetic and pulsation maxima can occur because the mode pulsates always in a direction orthogonal to the magnetic axis. The magnetic and pulsation maxima are always in quadrature.
(A.9)No possible coincidence between magnetic and pulsation maxima can occur because the mode pulsates always in a direction orthogonal to the magnetic axis. The magnetic and pulsation maxima are always in quadrature.
A.0.3. Circular polarization |ψ| = π/4
In the case of m = ± 1 modes in the rotation reference system, (ψ = ± π/4, γ = π/2), the light curve simplifies to the simple expression  (A.10)The phase of the light curve then takes the characteristic shape of straight lines of slope ± 1. This situation appears in Fig. 2.
(A.10)The phase of the light curve then takes the characteristic shape of straight lines of slope ± 1. This situation appears in Fig. 2.
Appendix B: Nature of extrema at Φ = Φo
The condition to ensure that the maxima are located at Φ = Φo is written 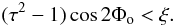 (B.1)The maxima correspond to the instants when the y-axis of the ellipse is the closest to the plane (i,Ω). We emphasize here that because of the orientation of the system (rotation axis and mode), these extrema are not located exactly at Φ = π/2 [π] , as we might think intuitively, but rather are phase shifted, except for γ = π/2 or i = π/2 for which they are located at Φ = π/2 [π] . Their amplitudes relative to the extrema at Φ = 0 are
(B.1)The maxima correspond to the instants when the y-axis of the ellipse is the closest to the plane (i,Ω). We emphasize here that because of the orientation of the system (rotation axis and mode), these extrema are not located exactly at Φ = π/2 [π] , as we might think intuitively, but rather are phase shifted, except for γ = π/2 or i = π/2 for which they are located at Φ = π/2 [π] . Their amplitudes relative to the extrema at Φ = 0 are
which do not vanish as long as the mode is not linearly polarized in the plane (B,Ω), i.e. τ = 0.
All Figures
 |
Fig. 1 The oblique pulsator model for dipole modes (Bigot & Dziembowski 2002). During the pulsation cycle, the axis of the dipole mode lies in a fixed plane that is inclined to both the rotation and magnetic axes. The shape of the displacement vector is elliptical. The two axes of the ellipse are the X-axis in the (B,Ω) plane and the perpendicular y-axis. The x-axis lies in the rotation equatorial plane. The line-of-sight of the observer makes an angle α(t) with the former, and σ(t) with the latter. The magnetic axis is inclined by the angle λ(t) to the line-of-sight. |
| In the text | |
 |
Fig. 2 Shapes of the light curves influenced by different inclinations and polarizations of the dipole mode. In both panels, the inclination of the observer is i = 70°. (Left panel) We consider a given polarization of the mode ψ = 5°, and compute curves for various inclinations of the mode plane: γ = 5° (—), 25° (···), 45° (− − −), 65° (−·−), 85° (−···−). It is clear that for all inclinations but one (γ = 5°), the phase jumps π radians exactly at the amplitude minima since the modes show the two hemispheres during the rotation period (i.e., this verifies the conditions given in Eq. (A.2)). The position of the minima at Φm are shifted by a change in the inclination of the mode, as one can check in Eq. (25). (Right panel) Shapes of the light curves influenced by different polarizations of the dipole mode. We consider a given inclination of the mode γ = 45°, and compute curves for various polarizations ψ of the dipole axis: ψ = 0° (—), 20° (···), 40° (− − −), 60° (−·−), 80° (−···−). In both panels, we have represented two periods of rotation. |
| In the text | |
 |
Fig. 3 Representation of the rotational variation of the light curves in amplitude and phase for three dipole modes on the six rows, and for three regimes of magnetic field in the three columns, μ = −0.2, −1.0 , and −5.0, where μ measures the ratio of the magnetic to centrifugal shifts of the pulsation frequencies. The amplitudes are normalized so that the maximum is equal to unity. In all cases, we choose i = 70° and β = 12°. The ratio of the Coriolis to centrifugal shifts of frequencies is χ = 0.01. See the text for a description of the properties of the three dipole modes. The values (in degrees) of the inclination and polarization are given for each mode in the brackets (γ,ψ) above the panels. |
| In the text | |
 |
Fig. 4 Applications to four roAp stars: HR 3831 (upper left), HD 6532 (upper right), α Cir (lower left), and HD 99563 (lower right). The dots represent the observed values and the full lines the theory. Observational data are from Kurtz et al. (1997a) for HR 3831, Kurtz et al. (1996a) for HD 6532, Bruntt et al. (2009) for α Cir, and Handler et al. (2006) for HD 99563. In our linear treatment of pulsation, the absolute amplitude of the mode is arbitrary. Therefore, the amplitudes of the light curves are scaled so that the observed ones equal the theoretical ones at Φ = 0. The theoretical pulsation phase is with respect to an arbitrary zero-point in time, so is shifted to reproduce the observed pulsation phase at rotation phase Φ = 0. The best-fits to these curves are (i = 68°, γ = 91°, ψ = −7°) for HR 3831, (i = 40°, γ = 70°, ψ = −15°) for HD 6532 (i = 37°, γ = 20°, ψ = 0.5°) for α Cir, and (i = 44°, γ = 86°, ψ = −9°) for HD 99563. The different shapes of the amplitudes are caused by different inclinations of the mode axes with respect to the line-of-sight of the observer. The four modes are almost linearly polarized. The rotational variabilities of the magnetic fields of HD 6532, α Cir, and HD 99563 are not known; such observations will thus test our model for agreement with the angles we have given. |
| In the text | |
 |
Fig. A.1 Representation of the light curves for linear polarized (ψ = 0) dipole modes with different inclinations of the pulsation axis. This illustrates the cases discussed in Sect. A.0.1. In both figures, the position of the observer is fixed, i = 40°. Left panel: the dipole axis remains close to the line-of-sight during the rotation of the star. The observer only sees one hemisphere of the mode, and thereby does not observe a phase jump during the rotation period. Hence, a maximum and minimum of the rotational envelope of the pulsation are observed at Φ = 0 and Φ = π. Right panel: the dipole axis is now sufficiently inclined with respect to the line-of-sight so that the two hemispheres of the dipole can been seen by the observer. A phase jump by π radians occurs when the node of the oscillations crosses the plane (i,Ω). In this case, the amplitude of the rotational envelope leads to two maxima of different amplitudes (α(0) < α(π)). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.