| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201015986 | |
| Published online | 24 January 2011 | |
Stellar metallicities beyond the Local Group: the potential of J-band spectroscopy with extremely large telescopes
1
UK Astronomy Technology Centre, Royal Observatory Edinburgh,
Blackford Hill,
Edinburgh
EH9 3HJ,
UK
e-mail: chris.evans@stfc.ac.uk
2
Rochester Institute of Technology, 54 Lomb Memorial Drive, Rochester, NY
14623,
USA
3
School of Physics & Astronomy, University of Leeds,
Woodhouse Lane,
Leeds, LS2 9JT, UK
4
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge, CB3 0HA, UK
5
Institute for Astronomy, University of Hawaii,
2680 Woodlawn
Drive, Honolulu,
HI
96822,
USA
6
Max-Planck-Institute for Astrophysics,
Karl-Schwarzschild-Str.
1, 85748
Garching,
Germany
7
GEPI, Observatoire de Paris, 5 place Jules Janssen, 92195
Meudon Cedex,
France
8
Key Laboratory of Optical Astronomy, National Astronomical
Observatories, Chinese Academy of Sciences, 20A Datun Road, Chaoyang District,
Beijing
100012, PR
China
9
LAM, OAMP, 38 rue Frédéric Joliot Curie,
13388
Marseille Cedex 13,
France
10
Department of Physics, Durham University,
South Road, Durham, DH1
3LE, UK
11
LESIA, Observatoire de Paris, 5 place Jules Janssen, 92195
Meudon Cedex,
France
Received: 23 October 2010
Accepted: 8 December 2010
We present simulated J-band spectroscopy of red giants and supergiants with a 42 m European Extremely Large Telescope (E-ELT), using tools developed toward the EAGLE Phase A instrument study. The simulated spectra are used to demonstrate the validity of the 1.15–1.22 μm region to recover accurate stellar metallicities from Solar and metal-poor (one tenth Solar) spectral templates. From tests at spectral resolving powers of four and ten thousand, we require continuum signal-to-noise ratios in excess of 50 (per two-pixel resolution element) to recover the input metallicity to within 0.1 dex. We highlight the potential of direct estimates of stellar metallicites (over the range − 1 < [Fe/H] < 0) of red giants with the E-ELT, reaching out to distances of ~ 5 Mpc for stars near the tip of the red giant branch. The same simulations are also used to illustrate the potential for quantitative spectroscopy of red supergiants beyond the Local Volume to tens of Mpc. Calcium triplet observations in the I-band are also simulated to provide a comparison with contemporary techniques. Assuming the EAGLE instrument parameters and simulated performances from adaptive optics, the J-band method is more sensitive in terms of recovering metallicity estimates for a given target. This appears very promising for ELT studies of red giants and supergiants, offering a direct metallicity tracer at a wavelength which is less affected by extinction than shortward diagnostics and, via adaptive optics, with better image quality.
Key words: instrumentation: adaptive optics / instrumentation: spectrographs / techniques: spectroscopic / Galaxy: stellar content / stars: fundamental parameters
© ESO, 2011
1. Introduction
Plans are well advanced for the next generation of optical and infrared (IR) ground-based telescopes, the extremely large telescopes (ELTs). Their science cases are broad, ranging from direct imaging of exoplanets, to studies of resolved stellar populations in external galaxies, and spectroscopy of distant “first light” galaxies at the highest redshifts (e.g. Hook et al. 2006).
The ELTs are an increasingly global effort, with three projects under detailed study – the Giant Magellan Telescope (GMT), the Thirty Meter Telescope (TMT), and the European Extremely Large Telescope (E-ELT). With primary apertures in excess of 20 m, they will deliver a huge gain in our capabilities via a combination of unprecedented sensitivity and exquisite angular resolution. In parallel to the design of the observatories, significant effort has also been invested in studies of ELT instrumentation (see Jaffe et al. 2010; Simard et al. 2010; Ramsay et al. 2010).
Over the past few years, deep imaging from ground-based telescopes and the Hubble Space Telescope (HST) has provided us with new and unique views of the outer regions of large galaxies beyond the Milky Way for the first time, such as M 31 (e.g. Ferguson et al. 2005) and M 33 (e.g. Barker et al. 2007). From analysis of the resulting photometry and colour-magnitude diagrams we can determine star-formation and assembly histories for external galaxies, enabling tests of theoretical models of galaxy evolution (e.g. Bullock & Johnston 2005), i.e. using resolved stellar populations as a tracer of the processes which have shaped the evolution of their host systems.
The imaging from the Advanced Camera for Surveys (ACS) Nearby Galaxy Survey Treasury (ANGST; Dalcanton et al. 2009) provides an excellent illustration of the diversity of galaxies beyond the Local Group. Crucially, the Local Volume includes a wide variety of morphological types – massive ellipticals, large metal-poor irregulars, lower-mass late-type spirals, interacting systems, dwarf starbursts – providing an excellent opportunity to quantify the effects of environment on galaxy evolution.
Photometric methods are powerful when applied to extragalactic stellar populations but follow-up spectroscopy can aid our understanding significantly via precise chemical abundances and stellar kinematics. For example, results from the spectroscopy of luminous blue supergiants in external galaxies obtained by the Araucaria project (Gieren et al. 2005a). However, in pursuit of spectroscopy of evolved stellar populations, the 8–10 m class telescopes are already near their limits beyond a few hundred kpc. For instance, observations with Keck-DEIMOS struggled to yield useful spectra below the tip of the red giant branch (TRGB) in M 31 at I > 21.5 (Chapman et al. 2006). If we aspire to spectroscopy of individual evolved stars in galaxies beyond the Local Group, we require the increased sensitivity of the ELTs, likely combined with some degree of correction from adaptive optics (AO) to mitigate the effects of crowding.
Indeed, for stellar spectroscopy with the ELTs there will be a fine balance in sensitivity between the improved image quality from AO as one goes to longer wavelengths (where the wavefront errors become less significant compared to the observed wavelengths) versus the increased sky background. Moreover, work over the past decades has provided an excellent understanding of many of the optical spectral lines available to us, enabling robust estimates of physical parameters and chemical abundances. To exploit the best performance (in terms of angular resolution) from the ELTs, we need to improve our knowledge of near-IR diagnostics, and also to pin-down the “sweet spot” in terms of the gain in sensitivity from AO versus the background contribution.
A recent study by Davies et al. (2010; hereafter DKF10) suggested new J-band diagnostics, spanning 1.15–1.22 μm (including lines from Mg, Si, Ti, and Fe), as a means to obtain stellar metallicities in extra-galactic red supergiants (RSGs). This wavelength region is relatively unexplored in this regard, only previously considered by Origlia et al. (2004). DKF10 noted that this method could be very powerful with new IR instruments under construction for 8–10 m class telescopes (such as VLT-KMOS and Keck-MOSFIRE), providing precise stellar abundances in galaxies out to a potential distance of ~ 10 Mpc, complementing those from luminous blue supergiants (e.g. Bresolin et al. 2001; Kudritzki et al. 2008). An even more compelling future prospect is in the context of ELT observations, with DKF10 noting the potential of direct abundance estimates for individual RSGs in galaxies even beyond the Local Volume (subject to crowding).
A second possible application of this spectral region is in observations of evolved red giant branch (RGB) stars – the long-lived descendants of much lower-mass stars. The marcs model atmospheres (Gustafsson et al. 2008) used by DKF10 are actually of red giants (see their Sect. 2.2 for a discussion of the applicability of these models over a large range of stellar luminosities).
The potential of a direct abundance diagnostic for J-band ELT observations of both young (RSG) and old (RGB) stellar populations in external galaxies – with the benefit of better AO correction compared to shorter wavelengths – warrants further exploration. EAGLE is a conceptual design of an AO-corrected, multi-IFU, near-IR spectrograph, undertaken as one of the Phase A instrument studies for the E-ELT (Cuby et al. 2010). In this article we employ tools developed in the course of the EAGLE study as a proof-of-concept for quantitative J-band spectroscopy with the ELTs.
We simulate EAGLE J-band observations with two objectives. First, to validate the technique of DKF10 for metal-poor spectral templates, and secondly, to explore the distances to which we could obtain robust abundance estimates (for both RGB stars and RSGs) with ELT observations. To compare these results with diagnostics already in common use, we also consider simulations in the I band. Sect. 2 describes the tools and assumptions used in the simulations, with the analysis presented in Sect. 3. In Sects. 4 and 5 we discuss the results in the context of the scientific potential of the E-ELT and other upcoming facilities.
2. Simulations
Three top-level science cases informed the requirements of the EAGLE design: the physics and evolution of high-redshift galaxies, characterization of “first light” galaxies at the highest redshifts, and studies of resolved stellar populations in the Local Volume. The specifications of the baseline design are summarised in Table 1 (with further discussion given by Evans et al. 2010b).
To investigate the critical requirements for spatially-resolved spectroscopy of high-redshift galaxies, Puech et al. (2008) developed a web-based tool to generate simulated IFU datacubes. This was used by Puech et al. (2008, 2010a) to investigate the required image quality, in terms of the level of AO correction, to recover spatially-resolved properties in high-redshift galaxies (up to z ~ 6). Functional details of the websim simulator are given by Puech et al. (2010b). In brief, there is a web-interface to a core idl code. The user uploads input datacubes in the Flexible Image Transport System (FITS) format, which must incorporate specific keywords in the headers to provide information to the code, as well as sufficient spatial sampling (typically ten times greater than the size of the final IFU pixel) and the desired spectral sampling. The input cubes are then convolved with a model point-spread function (PSF), selected from a list of AO simulations (Sect. 2.1) which are hard-wired into the code. By adopting the relevant instrument/telescope parameters, Puech et al. (2010a) provided an external check of the websim routines by reproducing datacubes to match those from SINFONI observations of high-redshift galaxies.
EAGLE baseline design.
The parameters used in the websim simulations are summarised in Table 2. The current E-ELT design features a primary with an equivalent diameter of 42 m and with approximately 9% obscuration by the secondary and supporting structures. The telescope throughput (≥80%) was the expected temporal average of the E-ELT design at the start of the EAGLE study, retained here as a worst-case estimate (compared to the ≥90% adopted by the Design Reference Mission studies, e.g., Puech et al. 2010a).
Inclusion of the sky background is discussed in detail by Puech et al. (2010a), in which a well-sampled model of the Mauna Kea background is scaled by measurements of the atmospheric absorption at Paranal; the same approach is used here. The E-ELT site was announced in early 2010 to be Cerro Armazones in northern Chile. Although at an altitude of 3060 m, slightly higher than Paranal (the site of the Very Large Telescope, VLT), the adopted sky model is a good enough approximation for our purposes.
The websim routines add the sky spectrum (which includes the OH emission lines) to each spatial element of the datacube, then a noise contribution is added. In parallel, a separate sky spectrum is constructed using a different realisation of the noise (i.e. a different random number seed), to simulate an observed sky spectrum, which might be obtained by dedicated IFUs, on-off dithers, or using object-free spatial pixels in the same IFU. Each sky spectrum is then subtracted from the science spectrum for each spatial element, producing a sky-subtracted output cube. This technique is idealised slightly in the sense that there is little difference between the simulated sky and that in the science data, which could lead to residuals in the case of strong variations of the OH lines. However, OH residuals are present in the simulated spectra due to differences in the added noise to the science and sky components.
In specifying the detector properties we adopted parameters from tests of Hawaii-2RG IR arrays by Finger et al. (2006): a dark current of 0.01 e−/pixel/s and a lowest read-out noise of 2.3 e−/pixel (achieved using “Fowler” sampling, see Fowler & Gatley 1990). Testing of the four Hawaii-2RG arrays destined for KMOS has yielded a read-noise of less than 10 e−/pixel from double-correlated sampling (Sharples et al. 2010); Fowler sampling of the same arrays should approach the best-case results from Finger et al. with existing technology. Detector development is ongoing in parallel to plans for the ELTs (e.g. development of 4k × 4k arrays), such that detector cosmetics/properties will not limit ELT observations of the type that we describe here. Long detector integration times (1800 s) were adopted, both for simplicity in the simulations and also to ensure that the observations at R = 10 000 are background limited (see Sect. 3.2.2 for further discussion).
Parameters used in the websim simulations.
Note that many of the targets for absorption-line spectroscopy with the ELTs are already known from deep HST imaging, but are beyond the reach of 8–10 m class facilities. Seeing-limited or Ground-Layer Adaptive Optics (GLAO) observations will not deliver sufficient contrast to match such imaging (e.g. Cunningham et al. 2008), whereas the EAGLE sampling is commensurate with the HST pixel scale – i.e. if a target is resolved with HST, then EAGLE is well-matched to provide follow-up. The Near-IR Camera (NIRCam) for the James Webb Space Telescope (JWST) also has a similar pixel scale.
In the densest regions in external galaxies or stellar clusters, finer angular resolution/greater contrast will be required (thus obtained over a smaller field). The spectroscopic methods discussed here will be equally valid for instruments aimed at probing finer scales such as HARMONI for the E-ELT (Thatte et al. 2010) and IRIS for the TMT (Larkin et al. 2010), but detailed performance simulations would require tailored PSFs, beyond the scope of the current work.
2.1. Simulated PSFs
The EAGLE concept employs multi-object adaptive optics (MOAO) to provide significantly improved image quality for selected target fields within the focal plane (first advanced for the FALCON concept, e.g. Assémat et al. 2007). The EAGLE baseline design uses an array of six laser guide stars (at a radius of  ) and five natural guide stars (NGS) to map the atmospheric turbulence (Rousset et al. 2010a). The adaptive mirror in the E-ELT (M4) will be used primarily to correct the ground-layer contribution, while the higher-altitude turbulence will be corrected by deformable mirrors in each science channel. The baseline design of EAGLE has an un-obstructed field-of-view with a diameter of 5′, but the regions between the optics to monitor the laser guide stars are also accessible, giving a total field-of-view equivalent to a diameter of 7′.
) and five natural guide stars (NGS) to map the atmospheric turbulence (Rousset et al. 2010a). The adaptive mirror in the E-ELT (M4) will be used primarily to correct the ground-layer contribution, while the higher-altitude turbulence will be corrected by deformable mirrors in each science channel. The baseline design of EAGLE has an un-obstructed field-of-view with a diameter of 5′, but the regions between the optics to monitor the laser guide stars are also accessible, giving a total field-of-view equivalent to a diameter of 7′.
An extensive set of MOAO simulations were calculated as part of the EAGLE study (Rousset et al. 2010a,b), paying particular attention to the location and magnitude of potential NGS (with R < 17) in the target fields. The PSFs used here were generated using the ONERA wide-field AO analytical code (Neichel et al. 2008) with two real NGS configurations which, given the spatial distribution and magnitude of the available guide stars, are illustrative of the range of likely performance. These were initially selected for high-redshift simulations, so were taken for two example pointings within the area of the XMM-Newton Large-scale Structure Survey (Pierre et al. 2004), as shown in Fig. 1. Five NGS were selected from those available in the “good” configuration (left-hand panel of Fig. 1, which includes one bright target with R = 10.5); only four NGS were available in the “poor” configuration. As discussed by Evans et al. (2010b), the capability to use NGS beyond a 5′ diameter leads to excellent sky coverage.
 |
Fig. 1 Configurations of potential natural guide stars (NGS) used in the simulated PSFs (labelled by their R-band magnitudes). The overlaid circles have diameters of 5′, 7.3′, and 10′. Left: “good” NGS configuration, with multiple stars available. Right: “poor” NGS configuration, with only four stars within the intermediate circle. |
In practise, the exact AO correction for each sub-field/target is a function of its location in the patrol field with respect to the NGS. Calculating tailored PSFs for each potential target is not practical, so we employ median PSFs (for both “good” and “poor” NGS configurations) derived from a grid of points across the EAGLE patrol field from the analytical code. Typical variations of the ensquared energy (EE) across the patrol field are of order ± 10% – a key part of the planning for such observations will be to optimise the selection of targets in terms of the expected AO performance.
Assuming a “Paranal-like” set of conditions, we considered two sets of seeing in the simulations (with the same vertical turbulence profile):  at λ = 0.5 μm at zenith (the mean VLT seeing; Sarazin et al. 2008) and
at λ = 0.5 μm at zenith (the mean VLT seeing; Sarazin et al. 2008) and 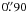 at a zenith distance (ZD) of 35°, illustrative of the performance that one might expect from execution of a “Large Programme”-like survey. The EE in 75 mas for each PSF is summarised in Table 3.
at a zenith distance (ZD) of 35°, illustrative of the performance that one might expect from execution of a “Large Programme”-like survey. The EE in 75 mas for each PSF is summarised in Table 3.
These performances are knowingly optimistic in the respect that fitting, tomography and noise errors were included, but additional error terms will contribute to the final performance. Rousset et al. (2010b) evaluated the additional wavefront error from these aberrations, which account for the limitations of the tomographic model, calibration, and operating in open loop. The EE degradation can be approximated by a factor of e−σφ2, where σφ2 is the phase variance (in radian2) of the wavefront error at the observed wavelength. This leads to a scaling of the EE in the simulated PSFs by a factor of 0.69 in H (calculated at 1.65 μm), 0.52 in J (1.25 μm), and 0.25 in I (0.85 μm). Although the morphology of the PSF will also change slightly, in calculation of the resulting signal-to-noise (S/N) ratios in the simulated spectra (next section) and interpretation of our results (Sect. 4) we consider only the more important equivalent loss in sensitivity. As noted before, the current study is primarily intended as a proof-of-concept study for the J-band diagnostics – the exact AO performances will continue to evolve with the telescope and instrument design, and experience from on-sky demonstrators such as CANARY on the William Herschel Telescope (e.g. Gendron et al. 2010).
Ensquared energy (EE) in 75 milliarcseconds in the simulated MOAO PSFs used in the I- and J-band simulations presented here.
2.2. Template spectra
Our simulations adopt two spectral templates from the grid of low-temperature stellar atmospheres calculated with the marcs code (Gustafsson et al. 2008). These have an effective temperature (Teff) of 3800 K (corresponding to an equivalent spectral type of approximately M0), log g = 0.0, and a microturbulence (ξ) of 2 km s-1. Models for two metallicities (Z) were used, with log [Z] = 0.0 and −1.0 (normalised to Solar). The latter model (i.e. 10% Solar) serves as a test of our methods in the low metallicity regime, comparable to, e.g., results for some of the young supergiants observed in the WLM dwarf irregular galaxy (Urbaneja et al. 2008). Further details of the marcs models, in the context of the current study, are given by DKF10.
At Solar metallicity we also calculated a set of I-band simulations to inform discussion of the J-band results in Sect. 4. The I-band includes the calcium triplet (CaT, spanning 0.85–0.87 μm), which has become an increasingly ubiquitous diagnostic of stellar metallicities and radial velocities in nearby galaxies (e.g. Tolstoy et al. 2004). The CaT is an empirical calibration of metallicity (which employs the equivalent width of the Ca ii lines) rather than a direct diagnostic. However, careful calibration yields a robust relationship over a large range of metallicity (−2.5 < [Fe/H] < −0.2; Cole et al. 2004). Our primary interest in the CaT is simply to obtain an estimate of the continuum sensitivities, so only one template (log [Z] = 0.0) is required.
The templates were convolved by the relevant spectral resolving power, and then binned such that each resolution element is sampled by two pixels. The templates were restricted to spectral windows of λλ1.15–1.22 μm (J-band) and λλ0.840–0.875 μm (I-band), with artificial continuum regions appended (with an intensity set to unity) to provide straightforward estimates of the S/N in the simulated spectra.
Summary of continuum signal-to-noise (S/N) obtained per two-pixel resolution element for simulated J-band spectroscopy (texp = 10 h, R = 4000 and 10 000).
The websim routines operate on fluxes (F) in physical units (either ergs/s/cm2/Hz or ergs/s/cm2/Å), so the input model templates were scaled to the desired observed magnitudes (M, in the Vega system), using:  (1)where F(I = 0) = 2550 Jy and F(J = 0) = 1600 Jy (Bessell 1979; Campins et al. 1985, respectively)1.
(1)where F(I = 0) = 2550 Jy and F(J = 0) = 1600 Jy (Bessell 1979; Campins et al. 1985, respectively)1.
The simulated IFU observations are of an isolated point source centred in the central (37.5 × 37.5 mas) spatial pixel, which is then extracted to yield the object spectrum for each target magnitude/set of conditions. The image quality of the simulated PSFs is sufficiently good that, in this idealised case of a centrally-located point source, extraction and merging with adjacent spatial elements does not improve the S/N of the final spectrum; in real EAGLE observations, more sophisticated extraction routines (e.g., PSF-fitting) would likely be required.
2.3. Simulation results
Each set of simulations was run ten times to provide a meaningful estimate of the dispersions in the derived metallicities and continuum S/N. Example simulated J-band spectra are shown in Figs. 2 and 3, with notable diagnostic lines of Mg i, Si i, Ti i and Fe i labelled. Example I-band spectra are shown in Fig. 4.
The means and standard deviations of the continuum S/N from the J- and I-band runs are summarised in Tables 4 and 5, respectively; the results are also shown in Figures 5–7. Following the discussion in Sect. 2.1 regarding the known limitations of the AO simulations, the quoted magnitudes take into account the factor of two in intensity in the J-band (equivalent to ΔJ = −0.75) and the factor of four in the I-band (equivalent to ΔI = −1.5), i.e. the effective magnitude of each simulation is brighter than the input magnitude. All quoted S/N results are for spectra extracted from the central spatial pixel of each cube, per two spectral pixels (set to be the sampling of the resolution element in each λ and R combination).
 |
Fig. 2 Examples of simulated R = 4000 spectra for J = 21.25, 22.25, and 23.25 (with seeing of |
 |
Fig. 3 Examples of simulated R = 10000 spectra for J = 21.25, 22.25, and 23.25 (with seeing of |
 |
Fig. 4 Examples of simulated CaT spectra (R = 10 000, log [Z] = 0.0) for I = 20.6, 21.6, and 22.6, (with seeing of |
Summary of continuum signal-to-noise (S/N) obtained per two-pixel resolution element for simulated I-band spectroscopy (texp = 10 h, R = 10 000).
 |
Fig. 5 Continuum signal-to-noise (S/N) results for simulated J-band spectroscopy (texp = 10 h, R = 4000) from Table 4. |
 |
Fig. 6 Continuum signal-to-noise (S/N) results for simulated J-band spectroscopy (texp = 10 h, R = 10 000) from Table 4. |
 |
Fig. 7 Continuum signal-to-noise (S/N) results for simulated I-band spectroscopy (texp = 10 h, R = 10 000) from Table 5. |
3. Analysis
3.1. J-band simulations
Our goal in the first part of the analysis is to determine physical properties from the simulated observations and compare them with those of the input model, i.e., how successfully can we recover accurate metallicities at both log [Z] = 0.0 and −1.0, and what S/N is required?
We follow similar methods to those described by DKF10. Each simulated spectrum is compared with template spectra from the marcs grid, the χ2 is calculated, and the location in the grid of the χ2 minimum is found. The parameter space searched includes 3200 < Teff < 4000 K (in steps of 200 K), −1.5 < log [Z] < +1.0 (in steps of 0.25 dex)2, 2 < ξ < 5 km s-1 (in steps of 1 km s-1)3, and log g = 0.0 and + 1.0.
Two refinements to the methods from DKF10 were necessary for the analysis presented here. This concerns the location of the continuum level in the simulated spectra and the interpolation between model grid points to refine the metallicity determinations, both of which are now discussed.
3.1.1. Continuum placement
To obtain accurate metallicities from the simulated spectra it is crucial that the continuum level is determined correctly. Placing the continuum at the wrong level results in an incorrect measurement of the normalised line strengths, thus an erroneous metallicity. DKF10 found the continuum level of their input spectra by ranking the spectral pixels in order of their (normalised) flux, and then finding the median value of those pixels with the greatest flux. In a spectrum comprised of continuum and absorption lines, the pixels with the greatest flux will have a value equivalent to the continuum level plus the noise. At high S/N this is a very good approximation of the continuum level, but at low S/N this can lead to the estimated continuum level being too high, resulting in a derived metallicity that is systematically above that of the input spectrum.
Here we adopt an improved method of continuum determination, assuming that the noise is Gaussian (i.e. requiring good sky subtraction). A spectrum of pure Gaussian noise, when ranked in order of increasing pixel value, will produce a trend which is approximately linear in the middle-ranking pixels (see Fig. 8). This linear regime is selected to contain the values that are within ~ 1σ of the mean. An absorption-line spectrum (i.e. discrete features combined with Gaussian noise) will also have this linear regime (see Fig. 9). By identifying and fitting these pixels, we can find those within some tolerance level of the fit. In principle we can then select those within ~ 1σ of the mean continuum level, and use them to fit the continuum. Figures 8 and 9 illustrate this procedure for a spectrum of pure Gaussian noise and for a template absorption-line spectrum with noise added (both with S/N = 50).
 |
Fig. 8 Illustration of the continuum-fitting procedure for a spectrum of pure Gaussian noise. Top panel: input spectrum with S/N = 50. Centre: input spectrum plotted in order of increasing pixel flux (the “pixel ranking” spectrum). The blue line is a fit to the linear regime, with pixels selected as part of that regime ( ± 1σ of the mean) in red. Bottom: input spectrum, with the pixels selected for continuum fitting indicated by red dots. The resulting continuum fit is shown by the solid blue line. |
 |
Fig. 9 As for Fig. 8, but now for the template absorption-line spectrum, with Gaussian noised added (such that S/N = 50). |
3.1.2. Refinement of the metallicity measurement
The marcs grid provides models at intervals of 0.25 dex between log [Z] = − 1.5 and + 1.0 (excepting − 1.25). Determining a finer estimate of the stellar metallicity requires that we interpolate within the model grid. DKF10 achieved this by taking a χ2-weighted mean of the best-fitting points in the grid. However, if the χ2 trend with metallicity is asymmetric about the χ2 minimum (i.e. the best-fitting value), the “refined” metallicity will always be systematically offset from the best-fitting value in the direction of the shallowest χ2 gradient. For example, if the χ2 minimum in the grid is at log [Z] = 0.0, but the χ2 diverges more rapidly at negative log [Z] than at positive values, the χ2-weighted mean metallicity will always be above 0.0. Indeed, in the course of the current study we found that determining stellar metallicities in this way produced “refined” estimates that were systematically larger than the input values (a consequence of the morphology of the χ2-minimum).
To eliminate these systematic errors we introduced a new method to refine the metallicity determination beyond the resolution of the model grid. After finding the location of the χ2 minimum in the grid, we extract a two-dimensional plane in Teff-log [Z] space at equal log g and ξ values. We then resample this grid onto a grid five times finer using bi-cubic spline interpolation, and take the location of the χ2 minimum of the resampled grid as the refined metallicity and stellar temperature.
3.2. Results
Each simulated spectrum was run through the atmospheric analysis code to determine Teff, log [Z] , ξ and log g. The mean metallicities recovered (and their standard deviations) from the ten runs of each simulation (for input metallicity, R, NGS configuration, seeing, and effective magnitude) are shown in Fig. 10.
3.2.1. R = 4000
The mean metalliticites recovered from the R = 4000 simulations have a small scatter around the input value (<0.1 dex) down to J = 22.75 (see Fig. 10). This is the point at which the errors start to become larger, although the dispersion is only ± 0.1–0.15 dex for J = 23.25 with  seeing.
seeing.
These results provide a good test of the DKF10 methods for metal poor stars, demonstrating reliable metallicity estimates at both metallicities above a given S/N threshold. Of course, S/N is not the only effect which determines the accuracy of the metallicity estimate. Other effects will likely play a role, such as the robustness of the atomic data, any degeneracy between temperature, surface gravity, and microturbulence, and which part of the curve-of-growth the selected lines are on (i.e. the effects of saturation on the observed equivalent width and its relation to abundance). Nevertheless, comparing these results with the S/N values in Table 4 suggests a minimum S/N of 50 to 60 is required to recover Z to within 0.1 dex.
 |
Fig. 10 Mean metallicities (and standard deviations) recovered from analysis of the simulated J-band spectra. Results are shown for the log [Z] = 0.0 and − 1.0 input templates, at R = 4000 and 10 000, for both seeing values ( |
3.2.2. R = 10 000
Analysis of the R = 10000 simulations also recovers good metallicity determinations (ΔZ ± 0.1 dex) for both templates. The minimum S/N threshold is marginally lower than for the R = 4000 spectra, with S/N ≳ 45 required from comparison with the results in Table 4.
Given the greater spectral dispersion, the faint magnitude limit is (at least) half a magnitude brighter than for the R = 4000 simulations. Thus, use of the lower resolving power is (as to be expected) the most sensitive option if just a global estimate of metallicity is required for a given target. However, if precise radial velocities are also required, to map the dynamics of a given region of the host galaxy, then observations at R = 10 000 provide improved velocity resolution (30 km s-1, as compared to 75 km s-1 at R = 4000).
To investigate the noise properties in the higher-resolution mode, the intermediate files from the websim were analysed. The sky background continuum counts (~60 photons/pixel for integrations of 1800 s) give a shot noise that is over three times greater than the adopted detector read-noise. The noise on the dark current is actually the more critical factor in this regard, but note that our adopted dark value is somewhat conservative (e.g., a factor of two greater than that measured for the arrays tested for JWST by Figer et al. 2004). Shorter integrations of 900 s remain background limited, although minimising the detector read-noise in this instance becomes an even more important requirement.
3.3. I-band simulations
Understanding the relative performances for I- and J-band ELT spectroscopy will be valuable when planning future observations. Exploratory simulations of the CaT were given by Evans et al. (2010a) to investigate the potential of EAGLE spectroscopy in this region. To inform discussion of the new J-band results, we revisited simulations of the CaT, now adopting the same marcs templates and seeing/NGS configurations as for the J-band simulations. The adopted instrument throughput is slightly lower at 0.85 μm (30%) compared to 1.175 μm (35%) in the final EAGLE design. As before, these values are not adopted to be definitive, but are representative of a near-IR instrument solution in which the primary performance requirements are at longer wavelengths. Table 5 summarises the mean continuum S/N (and standard deviations), per two-pixel resolution element, obtained from sets of ten simulated spectra calculated at half-magnitude intervals4.
As an external check on the simulated I-band performances we turn to the ESO E-ELT spectroscopic exposure time calculator (ETC)5. Input parameters were adopted to match those in the EAGLE simulations as closely as possible: a marcs model atmosphere with Teff = 4000 K, point-source target, Paranal site, 42 m primary, seeing of  , zenith distance = 30°, laser-tomography/multi-conjugate AO PSF, R = 10 000, a 20 mas radius of the S/N reference area (i.e. best match to our slice-width of 37 mas), and individual integration times of 1800 s. For S/N ≥ 10 (per two-pixel resolution element), the ETC requires 10 h of total integration time for I = 24.85. Note that the simulated PSFs incorporated in the ESO ETC have some of the same limitations to those generated for EAGLE, taking this into account leads to an effective I-band magnitude of ~ 23.5, i.e., of comparable sensitivity to the results in Table 5. Given the differences in the AO architectures, the exact modelling tools (and assumptions therein), and the methods used to calculate the S/N, the ETC comparison provides an independent check that our sensitivity limit (for a given S/N) is within the expected range.
, zenith distance = 30°, laser-tomography/multi-conjugate AO PSF, R = 10 000, a 20 mas radius of the S/N reference area (i.e. best match to our slice-width of 37 mas), and individual integration times of 1800 s. For S/N ≥ 10 (per two-pixel resolution element), the ETC requires 10 h of total integration time for I = 24.85. Note that the simulated PSFs incorporated in the ESO ETC have some of the same limitations to those generated for EAGLE, taking this into account leads to an effective I-band magnitude of ~ 23.5, i.e., of comparable sensitivity to the results in Table 5. Given the differences in the AO architectures, the exact modelling tools (and assumptions therein), and the methods used to calculate the S/N, the ETC comparison provides an independent check that our sensitivity limit (for a given S/N) is within the expected range.
4. Discussion: RGB stars
We now consider the simulation results in the context of the (unreddened) distances to which we can recover accurate metallicities from J- and I-band spectroscopy with the E-ELT. For reference, absolute I-band magnitudes (MI) for RGB stars span −1 < MI < −3, with typical colours of (I − J)0 ~ 0.7–0.8 (e.g. Girardi et al. 2002; Marigo et al. 2008). At the tip of the RGB absolute magnitudes extend up to MI = −4.
4.1. Potential for E-ELT and EAGLE
We require S/N ≳ 50 for accurate metallicities from the J-band. At R = 4000, the results in Table 4 provide sufficient S/N down to J = 22.75 to 23.25, depending on the NGS configuration and seeing. Taking the bright end of the RGB (adopting MJ = −3.75 from the colours above), this corresponds to an unreddened distance modulus of 27, or a distance of ~2.5 Mpc.
Thus, the DKF10 methods could provide a direct metallicity indicator in RGB stars out to a volume which encompasses a diverse range of galaxies. For instance, as we move beyond the Local Group, there are 32 known galaxies with distances in the range 1.0 < d ≤ 2.65 Mpc (Karachentsev et al. 2004). Most notably these include NGC 55 and NGC 300, the two spirals in the closer part of the Sculptor “Group” at 1.9 Mpc (Gieren et al. 2005b, 2008; Pietrzyński et al. 2006). NGC 55 is seen to have “LMC-like” abundances from spectroscopy of luminous supergiants (Castro et al. 2008, and in prep.) and NGC 300 has a radial oxygen gradient that ranges from 0.1 dex below Solar to near LMC levels at a radius of ~5 kpc (Bresolin et al. 2009, and references therein). This range of distances also includes lower-mass galaxies such as Sextans A, NGC 3109, and GR 8, which are all depleted in metals (as traced by oxygen) by approximately 1 dex (Kaufer et al. 2004; Evans et al. 2007; Van Zee et al. 2006, respectively). Of course, some galaxies within 2.5 Mpc, in addition to the faint dwarfs in the Local Group, will have even lower metallicities, providing motivation to further explore these diagnostics in the very metal-poor regime.
Scaling these results for TRGB stars (MJ ~ −5), good metallicities should be recoverable out to distances of 4 to 5 Mpc, depending on the exact AO correction. This opens-up an even wider range of targets, encompassing over 200 galaxies (Karachentsev et al. 2004), including those in the Centaurus A Group (e.g. Karachentsev et al. 2002). Direct metallicities for TRGB stars will play an important role in calibration of the distance scale in the local universe, reducing the uncertainties associated with photometric distance determinations from the TRGB method (see discussion by Kudritzki 2010), which can lead to systematic uncertatinies of ~5% (e.g. Mager et al. 2008).
4.2. Comparison with I-band performances
To compare the J-band results with the commonly used CaT diagnostic, we now consider the I-band performances given in Table 5. To determine the limiting magnitude for metallicities from our I-band simulations, we adopt a requirement of S/N ≥ 20 (per two-pixel resolution element). Battaglia et al. (2008) consider S/N ≥ 20 (per Å) as the threshold to obtain metallicities to within 0.1 dex from CaT spectroscopy at R = 6500 (from VLT-FLAMES). At the centre of our I-band template 1 Å is equivalent to 2.33 pixels, so the S/N results in Table 5 are slightly conservative in this regard, but they are also at greater spectral resolving power. However, the dominant factor here is the lower AO performance in the I-band than at longer wavelengths. The EE in the simulated PSFs is already considerably lower than in the J-band (Table 3), but the additional error terms are also larger (i.e. a factor of four compared to a factor of two in the J-band).
Depending on the seeing conditions and NGS configuration, the I-band simulations yield S/N ≥ 20 for 22.1 < I < 23.1, comparable to the J-band limit discussed in the previous section (S/N ≳ 50 at R = 4000). Given that RGB/TRGB stars are moderately red (I − J = 0.6–1.0), the DKF10 technique is probing deeper in terms of absolute luminosity of a given star.
The J-band technique exploits the improved AO correction at longer wavelengths. It requires greater S/N to recover a good estimate of stellar metallicity but, given the final EAGLE instrument throughputs and current expectations of AO performance shortwards of 1 μm, outperforms the CaT observations for a fixed exposure time of a given RGB star. In addition to a direct metallicity measurement (rather than the CaT calibration, albeit thought to be well understood), J-band observations will have the advantage of reduced extinction compared to observations at shorter wavelengths. Although we have limited ourselves to consideration of extra-galactic sources, working at longer wavelengths would be attractive for observations in, for example, obscured Galactic clusters.
4.3. Potential for TMT-IRMS
Our simulations can also be considered in the context of the Infra-Red Multi-Slit Spectrometer (IRMS) being developed for the TMT (Simard et al. 2010), which is a clone of the MOSFIRE instrument for the Keck I telescope. IRMS will be located behind the TMT multi-conjugate AO system (NFIRAOS), taking advantage of excellent image quality across a 2′ field. Its planned wavelength coverage is 0.9–2.5 μm and, depending on the slit-widths, the delivered resolving powers will be R = 3000 to 5000.
The minimum (Nyquist sampled) IRMS slit-width will be 160 mas, i.e. coarser spatial sampling and with a greater sky contribution for a point-source target than from EAGLE. The expected J-band encircled energies for a slit-width of 160 mas range from approximately 30 to 45%, depending on the position within the 2′ field (Dr. Brent Ellerbroek, priv. comm.). These simulations include some of the additional error terms factored into the discussion of our MOAO PSFs, i.e., when the larger IRMS slit-widths are taken into account, they provide a comparable range of image quality.
Assuming that the sensitivity varies as a factor of primary aperture (combined with a greater background flux from a larger effective slit), this corresponds to observations of RGB stars out to distances of ~1.5 Mpc and stars at the TRGB out to ~3 Mpc (depending on limitations of the NFIRAOS performance estimates cf. those discussed in Sect. 2.1). Tailored performance simulations are warranted for stellar spectroscopy specific to the TMT design, instrumentation and site (selected to be Mauna Kea in Hawaii). Nevertheless, we highlight the potential of the DKF10 methods for TMT spectroscopy of stellar populations beyond the Local Group. For example, in NGC 1569, a northern starburst galaxy at 1.95 Mpc (Karachentsev et al. 2004) with a metal abundance that appears to be intermediate to those of the LMC and SMC (Devost et al. 1997; Kobulnicky & Skillman 1997, cf., for example, Trundle et al. 2007). The TMT will also be well placed to explore the wealth of faint targets in northern hemisphere galaxies that are closer to home, e.g., M 31 and M 33.
5. Discussion: red supergiants
The work by DKF10 was originally motivated by spectroscopy of RSGs. With the benefit of AO correction and their intrinsically red colours, ELT observations of RSGs will provide our most distant quantitative tracers of individual “normal” stars. Extending the earlier discussion, and with absolute magnitudes of −7 < MJ < −11, J = 23.25 (at R = 4000) corresponds to an impressive 70 Mpc for the most luminous RSGs. The potential of such observations requires investigation in greater detail. In particular, the impact of crowding (and the required AO correction) will need to be assessed, for instance, using the HST observations of galaxies in the Virgo and Fornax Clusters (Côté et al. 2004; Jordán et al. 2007).
5.1. Potential for VLT-KMOS
More iminently, these results are relevant for KMOS (under construction for the VLT), which will have 24 IFUs, each  on the sky (with
on the sky (with  /slice), providing R = 3400 in the YJ bands (Sharples et al. 2010). The ETC for the natural-seeing mode of SINFONI provides the most appropriate comparison available at present – the limiting magnitude for S/N ~ 50, in a total exposure time of 10 h, is J = 18.75. As noted by DKF10, this will enable us to obtain surveys of RSGs in galaxies well beyond the Local Group, and for the brightest targets at distances of up to ~10 Mpc. This will provide the first opportunity to obtain large samples of RSGs to investigate large-scale metallicity gradients and structure in external galaxies.
/slice), providing R = 3400 in the YJ bands (Sharples et al. 2010). The ETC for the natural-seeing mode of SINFONI provides the most appropriate comparison available at present – the limiting magnitude for S/N ~ 50, in a total exposure time of 10 h, is J = 18.75. As noted by DKF10, this will enable us to obtain surveys of RSGs in galaxies well beyond the Local Group, and for the brightest targets at distances of up to ~10 Mpc. This will provide the first opportunity to obtain large samples of RSGs to investigate large-scale metallicity gradients and structure in external galaxies.
5.2. Potential for JWST-NIRSpec
These methods will also have applications with the JWST Near-IR Spectrometer (NIRSpec), which is a multi-object spectrograph capable of observing over 100 sources over a field of approximately 3.5 × 3.5 arcmin. NIRSpec will have three selectable spectral resolving powers (R = 100, 1000 and 2700), over a range of 1–5 μm.
The expected point-source NIRSpec sensitivity6 for S/N = 10 (two-pixel resolution element) with the R = 2700 grating, at 1.15 μm, is 950.7 nJy (equating to JVEGA = 23.1) in a total integration of 100 ks (27.8 h). This suggests a limiting magnitude of J = 19.6 (for S/N ~ 50) which, combined with the large multiplex of the mult-slit array, could obtain large samples of RSGs in galaxies out to the Virgo Cluster.
6. Summary
We have simulated J-band EAGLE/E-ELT observations of an M0 giant (and, by extrapolation of the model atmospheres, an M0 supergiant). We extended the work of DKF10 for the 1.15–1.22 μm diagnostic region, finding:
-
Robust stellar metallicities can be obtained from analysis ofJ-band spectra of metal-poor stars(log [Z] = −1.0).
-
Accurate metallicities (±0.1 dex, at log [Z] = −1.0 and 0.0) require: S/N ≥ 55 at R = 4000, and S/N ≥ 45 at R = 10 000.
-
The Phase A design of EAGLE on a 42 m E-ELT has the potential of direct metallicity estimates for RGB stars out to distances of ~2.5 Mpc, and for RSGs well beyond the Virgo and Fornax Clusters (subject to crowding).
-
For our instrument assumptions and simulations of relative AO performance, the J-band diagnostics are slightly more sensitive than the CaT (Δ mag ~ 0.5–1.0) for recovering metallicities of a given M0-type star. The J-band method also has the advantage of reduced extinction compared to the CaT region.
The first two of these points are not specific to EAGLE (nor dependent on the simulated PSFs used here), serving as a proof-of-concept for broader application of the methods advanced by DKF10. This part of the J-band is relatively free of OH emission lines compared to other parts of the near-IR, enhancing its potential for quantitative spectroscopy of extragalactic stellar populations with ELTs. This diagnostic range also has great potential for other upcoming facilities such as VLT-KMOS, JWST-NIRSpec, and TMT-IRMS.
One of the prime drivers for inclusion of the I-band in the design of near-IR spectrographs for ELTs is to study extragalactic stellar abundances via the CaT. If comparable or better results can be obtained from the J-band, inclusion of the I-band would become less critical, leading to simpler and potentially cheaper instrument designs (e.g. fewer gratings), and avoiding compromises which may detract from the potential performance at longer wavelengths.
As noted by DKF10, an important next step is quantitative analysis of RSGs in the Magellanic Clouds to refine these techniques over a range of metallicities, and to also extend this work to RGB stars in the Clouds. These methods should also be explored at yet lower metallicities (relevant to the study of metal-poor galaxy halos), both via analysis of metal-poor observations, and by use of a larger grid of theoretical calculations.
Diagnostics in the H- and K-bands (in which the AO correction will be even better) also warrant consideration in this context. For instance, use of K-band equivalent-width indices to estimate stellar metallicities (Frogel et al. 2001), and detailed abundance analysis of red giants (Origlia et al. 2002; Origlia & Rich 2004), and supergiants (Davies et al. 2009a,b) at greater resolving powers in the H-band.
The passband of Cousins I is somewhat different to that of the F814W HST filters, but the typical magnitude offset is small: I − F814W ≤ 0.05m (Holtzman et al. 1995).
The simulations were originally calculated adopting the I-band zero-point from the HST-NICMOS conversion tools: http://www.stsci.edu/hst/nicmos/tools/conversion_help.html (2250 Jy at 0.9 μm). Translated to the Bessell (1979) system this results in a shift of 0.1m fainter, hence the sampling in Table 5.
Acknowledgments
We thank François Assémat for his work on the EAGLE AO study, Brent Ellerbroek for updated information on the TMT simulations, and the referee for their constructive comments on the manuscript. B.D. is funded by a fellowship from the Royal Astronomical Society. R.P.K. acknowledges support from the Alexander-von-Humboldt Foundation. M.P., J.G.C. and G.R. acknowledge support from the Agence Nationale de la Recherche under contract ANR-06-BLAN-0191. D.F. is supported by NASA under award NNG 05-GC37G, through the Long Term Space Astrophysics program, and by a NYSTAR Faculty Development Program grant.
References
- Assémat, F., Gendron, E., & Hammer, F. 2007, MNRAS, 376, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, M. K., Sarajedini, A., Geisler, D., et al. 2007, AJ, 133, 1125 [Google Scholar]
- Battaglia, G., Irwin, M., Tolstoy, E., et al. 2008, MNRAS, 383, 183 [Google Scholar]
- Bessell, M. S. 1979, PASP, 91, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Kudritzki, R.-P., Mendez, R. H., & Przybilla, N. 2001, ApJ, 548, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Gieren, W., Kudritzki, R.-P., et al. 2009, ApJ, 700, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., & Johnston, K. V. 2005, ApJ, 635, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Campins, H., Rieke, G. H., & Lebofsky, M. J. 1985, AJ, 90, 896 [NASA ADS] [CrossRef] [Google Scholar]
- Castro, N., Herrero, A., Garcia, M., et al. 2008, A&A, 485, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chapman, S. C., Ibata, R., Lewis, G. F., et al. 2006, ApJ, 653, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, A. A., Smecker-Hane, T. A., Tolstoy, E., Bosler, T. L., & Gallagher, J. S. 2004, MNRAS, 347, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Côté, P., Blakeslee, J. P., Ferrarese, L., et al. 2004, ApJS, 153, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Cuby, J.-G., Morris, S. L., Fusco, T., et al. 2010, Proc. SPIE, 7735, 80 [NASA ADS] [Google Scholar]
- Cunningham, C. R., Evans, C. J., Monnet, G., & Le Louarn, M. 2008, Proc. SPIE, 6986, 20 [NASA ADS] [Google Scholar]
- Dalcanton, J. J., Williams, B. F., Seth, A. C., et al. 2009, ApJS, 183, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., Origlia, L., Kudritzki, R.-P., et al. 2009a, MNRAS, 694, 46 [Google Scholar]
- Davies, B., Origlia, L., Kudritzki, R.-P., et al. 2009b, ApJ, 696, 2014 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, B., Kudritzki, R.-P., & Figer, D. F. 2010, MNRAS, 407, 1203 [DKF10] [NASA ADS] [CrossRef] [Google Scholar]
- Devost, D., Roy, J.-R., & Drissen, L. 1997, ApJ, 482, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. J., Bresolin, F., Urbaneja, M. A., et al. 2007, ApJ, 659, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. J., Yang, Y., Puech, M., et al. 2010a, in AO for ELTs, ed. Y. Clénet, J.-M. Conan, T. Fusco, & G. Rousset, EDP Sciences [arXiv:0909.1748] [Google Scholar]
- Evans, C. J., Lehnert, M. D., Cuby, J.-G., et al. 2010b, Proc. SPIE, 7735, 178 [NASA ADS] [Google Scholar]
- Ferguson, A. M. N., Johnson, R. A., Faria, D. C., et al. 2005, ApJ, 622, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Figer, D. F., Rauscher, B. J., & Regan, M. W. 2004, Proc. SPIE, 5167, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Finger, G., Garnett, J., Bezawada, N., et al. 2006, Nucl. Instr. Methods Phys. Res., 565, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Fowler, A. M., & Gatley, I. 1990, ApJ, 353, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Frogel, J. A., Stephens, A., Ramírez, S., & DePoy, D. L. 2001, AJ, 122, 1896 [NASA ADS] [CrossRef] [Google Scholar]
- Gendron, E., Morris, T., Hubert, Z., et al. 2010, SPIE, 7736, 23 [NASA ADS] [Google Scholar]
- Gieren, W., Pietrzyński, G., Bresolin, F., et al. 2005a, Msgnr, 121, 23 [Google Scholar]
- Gieren, W., Pietrzyński, G., Soszyński, I., et al. 2005b, ApJ, 628, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Gieren, W., Pietrzyński, G., Soszyński, I., et al. 2008, ApJ, 672, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holtzman, J. A., Burrows, C. J., Casertano, S., et al. 1995, PASP, 107, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Hook, I., Dalton, G., & Gilmozzi, R. 2006, Proc. SPIE, 6267, 69 [NASA ADS] [Google Scholar]
- Jaffe, D. T., DePoy, D. L., Fabricant, D. G., et al. 2010, Proc. SPIE, 7735, 72 [NASA ADS] [Google Scholar]
- Jordán, A., Blakeslee, J. P., Côté, P., et al. 2007, ApJS, 169, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Sharina, M. E., Dolphin, A. E., et al. 2002, A&A, 385, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karachentsev, I. D., Karachentsev, V. E., Huchtmeier, W. K., & Makarov, D. I. 2004, AJ, 127, 2031 [Google Scholar]
- Kaufer, A., Venn, K., Tolstoy, E., Pinte, C., & Kudritzki, R.-P. 2004, AJ, 127, 2723 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Skillman, E. D. 1997, ApJ, 489, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P. 2010, AN, 331, 459 [Google Scholar]
- Kudritzki, R.-P., Urbaneja, M. A., Bresolin, F., et al. 2008, ApJ, 681, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Larkin, J. E., Moore, A. M., Barton, E. J., et al. 2010, Proc. SPIE, 7735, 76 [NASA ADS] [Google Scholar]
- Mager, V. A., Madore, B. F., & Freedman, W. L. 2008, ApJ, 689, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neichel, B., Fusco, T., & Conan, J.-M. 2008, JOSAA, 26, 219 [Google Scholar]
- Origlia, L., & Rich, R. M. 2004, AJ, 127, 3422 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Rich, R. M., & Castro, S. 2002, AJ, 123, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Ranalli, P., Comastri, A., & Maiolino, R. 2004, ApJ, 606, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Pierre, M., Valtchanov, I., Altieri, B., et al. 2004, JCAP, 9, 11 [Google Scholar]
- Pietrzyński, G., Gieren, W., Soszyński, I., et al. 2006, AJ, 132, 2556 [NASA ADS] [CrossRef] [Google Scholar]
- Puech, M., Flores, H., Lehnert, M., et al. 2008, MNRAS, 390, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Puech, M., Rosati, P., Toft, S., et al. 2010a, MNRAS, 402, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Puech, M., Yang, Y., & Flores, H. 2010b, Proc. SPIE, 7735, 183 [NASA ADS] [Google Scholar]
- Ramsay, S. K., D’Odorico, S., Casali, M., et al. 2010, Proc. SPIE, 7735, 71 [NASA ADS] [Google Scholar]
- Rousset, G., Fusco, T., Assémat, F., et al. 2010a, in AO for ELTs, ed. Y. Clénet, J.-M. Conan, T. Fusco, & G. Rousset, EDP Sciences [arXiv:1002.2077] [Google Scholar]
- Rousset, G., Fusco, T., Assémat, F., et al. 2010b, Proc. SPIE, 7736, 25 [NASA ADS] [Google Scholar]
- Sarazin, M., Melnick, J., Navarrete, J., & Lombardi, G. 2008, Msngr, 132, 11 [Google Scholar]
- Sharples, R., Bender, R., Agudo Berbel, A., et al. 2010, Proc. SPIE, 7735, 39 [NASA ADS] [Google Scholar]
- Simard, L., Crampton, D., Ellerbroek, B., & Boyer, C. 2010, Proc. SPIE, 7735, 70 [NASA ADS] [Google Scholar]
- Thatte, N., Tecza, M., Clarke, F., et al. 2010, Proc. SPIE, 7735, 85 [NASA ADS] [Google Scholar]
- Tolstoy, E., Irwin, M. J., Helmi, A., et al. 2004, ApJ, 617, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Trundle, C., Dufton, P. L., Hunter, I., et al. 2007, A&A, 471, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urbaneja, M. A., Kudritzki, R.-P., Bresolin, F., et al. 2008, ApJ, 684, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Van Zee, L., Skillman, E. D., & Haynes, M. P. 2006, ApJ, 637, 269 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Ensquared energy (EE) in 75 milliarcseconds in the simulated MOAO PSFs used in the I- and J-band simulations presented here.
Summary of continuum signal-to-noise (S/N) obtained per two-pixel resolution element for simulated J-band spectroscopy (texp = 10 h, R = 4000 and 10 000).
Summary of continuum signal-to-noise (S/N) obtained per two-pixel resolution element for simulated I-band spectroscopy (texp = 10 h, R = 10 000).
All Figures
 |
Fig. 1 Configurations of potential natural guide stars (NGS) used in the simulated PSFs (labelled by their R-band magnitudes). The overlaid circles have diameters of 5′, 7.3′, and 10′. Left: “good” NGS configuration, with multiple stars available. Right: “poor” NGS configuration, with only four stars within the intermediate circle. |
| In the text | |
 |
Fig. 2 Examples of simulated R = 4000 spectra for J = 21.25, 22.25, and 23.25 (with seeing of |
| In the text | |
 |
Fig. 3 Examples of simulated R = 10000 spectra for J = 21.25, 22.25, and 23.25 (with seeing of |
| In the text | |
 |
Fig. 4 Examples of simulated CaT spectra (R = 10 000, log [Z] = 0.0) for I = 20.6, 21.6, and 22.6, (with seeing of |
| In the text | |
 |
Fig. 5 Continuum signal-to-noise (S/N) results for simulated J-band spectroscopy (texp = 10 h, R = 4000) from Table 4. |
| In the text | |
 |
Fig. 6 Continuum signal-to-noise (S/N) results for simulated J-band spectroscopy (texp = 10 h, R = 10 000) from Table 4. |
| In the text | |
 |
Fig. 7 Continuum signal-to-noise (S/N) results for simulated I-band spectroscopy (texp = 10 h, R = 10 000) from Table 5. |
| In the text | |
 |
Fig. 8 Illustration of the continuum-fitting procedure for a spectrum of pure Gaussian noise. Top panel: input spectrum with S/N = 50. Centre: input spectrum plotted in order of increasing pixel flux (the “pixel ranking” spectrum). The blue line is a fit to the linear regime, with pixels selected as part of that regime ( ± 1σ of the mean) in red. Bottom: input spectrum, with the pixels selected for continuum fitting indicated by red dots. The resulting continuum fit is shown by the solid blue line. |
| In the text | |
 |
Fig. 9 As for Fig. 8, but now for the template absorption-line spectrum, with Gaussian noised added (such that S/N = 50). |
| In the text | |
 |
Fig. 10 Mean metallicities (and standard deviations) recovered from analysis of the simulated J-band spectra. Results are shown for the log [Z] = 0.0 and − 1.0 input templates, at R = 4000 and 10 000, for both seeing values ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



