| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 13 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201014962 | |
| Published online | 16 September 2010 | |
Strong lensing in the MARENOSTRUM UNIVERSE
II. Scaling relations and optical depths
C. Fedeli1,2,3 - M. Meneghetti2,3 - S. Gottlöber4 - G. Yepes5
1 - Dipartimento di Astronomia, Università di Bologna,
via Ranzani 1, 40127 Bologna, Italy
2 - INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 - INFN, Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
4 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
5 -
Grupo de Astrofísica, Universidad Autónoma de Madrid, 28049 Madrid, Spain
Received 10 May 2010 / Accepted 7 July 2010
Abstract
The strong lensing events that are observed in compact clusters of
galaxies can, both statistically and individually, return important
clues about the structural properties of the most massive structures in
the Universe. Substantial work is ongoing in order to understand the
degree of similarity between the lensing cluster population and the
population of clusters as a whole, with members of the former being
likely more massive, compact, and substructured than members of the
latter. In this work we exploit synthetic clusters extracted from the M
AREN OSTRUM U NIVERSE
cosmological simulation in order to estimate the correlation between
the strong lensing efficiency and other bulk properties of lensing
clusters, such as the virial mass and the bolometric X-ray luminosity.
We found that a positive correlation exist between all these
quantities, with the substantial scatter being smaller for the
luminosity-cross section relation. We additionally used the relation
between the lensing efficiency and the virial mass in order to
construct a synthetic optical depth that agrees well with the true one,
while being extremely faster to be evaluated. We finally estimated what
fraction of the total giant arc abundance is recovered when galaxy
clusters are selected according to their dynamical activity or their
X-ray luminosity. Our results show that there is a high probability for
high-redshift strong lensing clusters to be substantially far away from
dynamical equilibrium, and that 30-40% of the total amount of giant
arcs are lost if looking only at very X-ray luminous objects.
Key words: gravitational lensing: strong - galaxies: clusters: general
1 Introduction
Explaining the process of cosmic structure formation is one of the major successes of the standard model for cosmology. Accordingly, tiny dark matter density fluctuations produced during the inflationary era grew up due to gravitational instability, eventually detaching from the overall expansion of the Universe and collapsing into bound structures. The observed statistical properties of these objects can help to understand the large scale matter distribution, and the way in which this has evolved during the history of the Universe.
Gravitational lensing is one of the most powerful tools for studying the formation of cosmic structures in general, and the mass assembly history of the most massive ones, galaxy clusters, in particular. Weak gravitational lensing can be used to perform non-parametric reconstruction of the outer dark matter halo profile (Kaiser et al. 1995; Bartelmann & Schneider 2001; Oguri et al. 2009), while strong lensing allow to put constraints on the inner slope (Richard et al. 2010), that is one of the main theoretical predictions of the cold dark matter paradigm. The statistics of strong lensing images also is a particularly interesting tool for the study of structure formation, since it is sensitive to both the abundance of galaxy clusters and their average inner structure. It is hence expected to give important hints on the assembly history of cosmic structures as well as on the background cosmology (Bartelmann et al. 2003).
Much work has been devoted in the past decade to the gravitational arc
statistics, that is the abundance of strongly elongated images that are
produced by galaxy clusters when acting as gravitational lenses on
background galaxies. Early results pointed toward a deficit of observed
arcs with respect to the theoretical predictions for a standard ![]() CDM cosmology (Bartelmann et al. 1998; Le Fevre et al. 1994; Luppino et al. 1999), which neither baryonic physics (Puchwein et al. 2005; Hilbert et al. 2008; Wambsganss et al. 2008), nor substructure (Meneghetti et al. 2003a,2000) and cluster mergers (Fedeli & Bartelmann 2007; Fedeli et al. 2006) seemed able to cure. Whether this discrepancy survives nowadays is unclear (Fedeli et al. 2008),
however this issue propelled substantial effort in order to better
understand the cluster population responsible for strong lensing
events, and to what degree this ensemble differs from the overall
cluster population (Meneghetti et al. 2010; Hennawi et al. 2007).
Moreover, considerable work has been done on the observational side as
well, in order to explore the high-redshift tail of the cluster lens
population (Gladders et al. 2003; Zaritsky & Gonzalez 2003), and to pave the way toward machine-based gravitational arc finding (Lenzen et al. 2004; Seidel & Bartelmann 2007).
CDM cosmology (Bartelmann et al. 1998; Le Fevre et al. 1994; Luppino et al. 1999), which neither baryonic physics (Puchwein et al. 2005; Hilbert et al. 2008; Wambsganss et al. 2008), nor substructure (Meneghetti et al. 2003a,2000) and cluster mergers (Fedeli & Bartelmann 2007; Fedeli et al. 2006) seemed able to cure. Whether this discrepancy survives nowadays is unclear (Fedeli et al. 2008),
however this issue propelled substantial effort in order to better
understand the cluster population responsible for strong lensing
events, and to what degree this ensemble differs from the overall
cluster population (Meneghetti et al. 2010; Hennawi et al. 2007).
Moreover, considerable work has been done on the observational side as
well, in order to explore the high-redshift tail of the cluster lens
population (Gladders et al. 2003; Zaritsky & Gonzalez 2003), and to pave the way toward machine-based gravitational arc finding (Lenzen et al. 2004; Seidel & Bartelmann 2007).
The dependence of the cluster lensing efficiency on the inner structure, dynamical state and merger activity of individual objects has been thoroughly studied (Meneghetti et al. 2007; Torri et al. 2004). An important issue that has been however scarcely investigated about strong lensing cluster is how the lensing efficiency correlates with bulk cluster properties, such as mass or X-ray luminosity. This aspect is extremely interesting, since it allows to better quantify the statistical properties of the cluster lens population, and in principle would allow to directly map the abundance of galaxy clusters into the arc abundance on the sky without intermediate calculations. In this work we tackle this issue making use of the large M AREN OSTRUM U NIVERSE cosmological simulation. This simulation contains adiabatic gas in addition to dark matter, and hence allows to characterize the cluster lens population taking into account the role of baryonic physics on structure formation. We additionally estimated the optical depth of the whole cluster population, which allows to compute the total number of arcs expected in the sky, and how this depends on selection biases such as the dynamical state or the X-ray luminosity.
The rest of this paper is organized as follows. In Sect. 2 we summarize the properties of the M AREN OSTRUM U NIVERSE simulation, and the calculations relevant for strong lensing of simulated clusters. Further details on this can be found in Meneghetti et al. (2010). In Sect. 3 we summarize the redshift distributions of the strong lensing cluster population. In Sect. 4 we report our results and in Sect. 5 we summarize our conclusions. In the remainder of this work, we refer to Meneghetti et al. (2010) as to Paper I.
2 Lensing in the MARENOSTRUM UNIVERSE simulation
The M AREN OSTRUM U NIVERSE (Gottlöber & Yepes 2007) is a large scale non-radiative SPH cosmological simulation performed with the publicly available code G ADGET2 (Springel 2005). The simulation box has a comoving side of 500 Mpc h-1 and contains
![]() particles, equally subdivided in number between dark matter and baryons. The mass of each dark matter particle equals
particles, equally subdivided in number between dark matter and baryons. The mass of each dark matter particle equals
![]() h-1, and that of each gas particle, for which only adiabatic physics is implemented, is
h-1, and that of each gas particle, for which only adiabatic physics is implemented, is
![]() h-1. The cosmological parameters of the simulation are in agreement with the WMAP-1 year data release (Spergel et al. 2003), namely
h-1. The cosmological parameters of the simulation are in agreement with the WMAP-1 year data release (Spergel et al. 2003), namely
![]() ,
,
![]() and
and
![]() with a scale invariant primordial power spectrum. The baryon density parameter is set to
with a scale invariant primordial power spectrum. The baryon density parameter is set to
![]() .
How this parameter set deal with the later WMAP releases (Komatsu et al. 2009; Spergel et al. 2007; Komatsu et al. 2010) is discussed in Sect. 5. In the following we describe only the main issues of our strong lensing analysis, deferring further detail to Paper I.
.
How this parameter set deal with the later WMAP releases (Komatsu et al. 2009; Spergel et al. 2007; Komatsu et al. 2010) is discussed in Sect. 5. In the following we describe only the main issues of our strong lensing analysis, deferring further detail to Paper I.
Bound structures within the simulation at each redshift snapshot were identified with a FOF algorithm (Klypin et al. 1999) with a basic linking length of 0.17 times the mean interparticle distance. All the FOF groups with mass larger than
![]() h-1 were then stored into sub-boxes of cubic shape with side length 5 Mpc h-1
for the subsequent lensing analysis. For each structure, the
three-dimensional density field was computed on a regular grid inside
the relative sub-box, and then projected along the three orthogonal
coordinate axes. Bundles of light rays were than traced through the
central part of each plane (Meneghetti et al. 2007),
evaluating for each of them the deflection angle as the sum of the
contributions given by each surface density cell. The final deflection
angle map has a side length of 1.5 Mpc h-1, which allows to fairly capture the details of the critical line structure (if present).
h-1 were then stored into sub-boxes of cubic shape with side length 5 Mpc h-1
for the subsequent lensing analysis. For each structure, the
three-dimensional density field was computed on a regular grid inside
the relative sub-box, and then projected along the three orthogonal
coordinate axes. Bundles of light rays were than traced through the
central part of each plane (Meneghetti et al. 2007),
evaluating for each of them the deflection angle as the sum of the
contributions given by each surface density cell. The final deflection
angle map has a side length of 1.5 Mpc h-1, which allows to fairly capture the details of the critical line structure (if present).
A preliminary analysis, performed with low resolution deflection angle
maps has shown that 49 366 clusters were able of producing
critical lines for sources at
![]() in at least one projection. For each of the projections of these
clusters we computed high resolution deflection angle maps for the
subsequent strong lensing analysis. We evaluated the cross sections
in at least one projection. For each of the projections of these
clusters we computed high resolution deflection angle maps for the
subsequent strong lensing analysis. We evaluated the cross sections
![]() for arcs with length-to-width ratio
for arcs with length-to-width ratio ![]() by adopting the semi-analytic algorithm of Fedeli et al. (2006).
Such algorithm reproduces well the results of fully numerical lensing
simulations, while being substantially faster. Moreover, being based
only on the properties of the deflection angle map, it is equally
applicable to analytic (Fedeli & Bartelmann 2007)
and to numerical lenses. For such computations the equivalent angular
size of sources was kept fixed to 0.5 arcsec, and the ellipticity
thereof was randomly drawn in the interval [0,0.5]. Given the extremely
large number of projections that we considered, we were forced to
examine only one single length-to-width threshold, R0 = 7.5, and one individual source redshift, that we set to
by adopting the semi-analytic algorithm of Fedeli et al. (2006).
Such algorithm reproduces well the results of fully numerical lensing
simulations, while being substantially faster. Moreover, being based
only on the properties of the deflection angle map, it is equally
applicable to analytic (Fedeli & Bartelmann 2007)
and to numerical lenses. For such computations the equivalent angular
size of sources was kept fixed to 0.5 arcsec, and the ellipticity
thereof was randomly drawn in the interval [0,0.5]. Given the extremely
large number of projections that we considered, we were forced to
examine only one single length-to-width threshold, R0 = 7.5, and one individual source redshift, that we set to
![]() .
These choices are rather common in strong lensing statistics studies, with R0=7.5 being a fair compromise between having good number statistics and strongly distorted images, and
.
These choices are rather common in strong lensing statistics studies, with R0=7.5 being a fair compromise between having good number statistics and strongly distorted images, and
![]() being typical for many real strong lensing clusters (see, e.g., Limousin et al. 2008; Elíasdóttir et al. 2007). Of the 148 098 (=
being typical for many real strong lensing clusters (see, e.g., Limousin et al. 2008; Elíasdóttir et al. 2007). Of the 148 098 (=
![]() )
projections that we have analyzed, only 11 347 produced a
non-vanishing cross section. This number is however by far the largest
ever considered for theoretical strong lensing studies to date.
)
projections that we have analyzed, only 11 347 produced a
non-vanishing cross section. This number is however by far the largest
ever considered for theoretical strong lensing studies to date.
The total number of arcs in the sky with ![]() that are produced by galaxy clusters that lens sources at a given redshift
that are produced by galaxy clusters that lens sources at a given redshift ![]() ,
and that are visible below some limiting magnitude cut
,
and that are visible below some limiting magnitude cut
![]() ,
is given by
,
is given by
![]() ,
where
,
where
![]() is the number of sources that, in the unit solid angle, have redshift
is the number of sources that, in the unit solid angle, have redshift ![]() and magnitude below the limit
and magnitude below the limit
![]() .
Note that, in order for this estimate to be self-consistent, the number
density has to be always corrected for the lensing magnification bias (Bartelmann & Schneider 2001; Fedeli et al. 2008).
This bias has the effect of increasing the angular density of visible
sources if the intrinsic number counts are steep enough, while
decreasing it if the number counts are relatively shallow.
.
Note that, in order for this estimate to be self-consistent, the number
density has to be always corrected for the lensing magnification bias (Bartelmann & Schneider 2001; Fedeli et al. 2008).
This bias has the effect of increasing the angular density of visible
sources if the intrinsic number counts are steep enough, while
decreasing it if the number counts are relatively shallow.
The optical depth for long and thin arcs produced by sources at redshift ![]() is instead defined as
is instead defined as
where N(M,z) represents the total number of structures present in the unit redshift around z and in the unit mass around M. The function
When only a finite discrete set of masses is available, as is the
case here and in all the numerical or semi-analytic studies, then the
Eq. (1) reduces to
where
![\begin{displaymath}\bar{\sigma}_{R_0,i}^* \equiv \frac{1}{2} \left[ \bar{\sigma}_{R_0}(M_i,z) + \bar{\sigma}_{R_0}(M_{i+1},z) \right]\cdot
\end{displaymath}](/articles/aa/full_html/2010/11/aa14962-10/img30.png)
|
(3) |
In practice, this approach is equivalent to assigning the average cross section of clusters with masses Mi and Mi+1 to all structures with mass between Mi and Mi+1. The optical depth presented in Eq. (1) will be a central quantity in the rest of our study and, as mentioned above, we shall set R0 = 7.5 henceforth.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14962f1}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg31.png)
|
Figure 1: The redshift distributions of strong lensing clusters in the M AREN OSTRUM U NIVERSE. The black histogram considers all clusters displaying critical lines, the red one those with a non-vanishing cross section for giant arcs, and the blue one those expected to produce at least one giant arc on average. The thick solid green curve represents the lensing efficiency, given by the normalized lensing distance, while the dashed one represents the lensing efficiency weighted for the cluster abundance (see the text for details). |
| Open with DEXTER | |
3 The population of strong lensing clusters
We begin by reporting the distribution in redshift of the galaxy
clusters that are capable of strongly lens background sources in the M AREN OSTRUM U NIVERSE.
As done in Paper I we selected three subsamples of such clusters: i)
clusters that are capable of producing critical curves;
ii) clusters that have a non-vanishing cross section; and
iii) clusters that, given suitable background source number
counts, are expected to produce at least one giant gravitational arc on
average. The cross section of this last class of objects should be
around
![]() Mpc2 h-2.
Obviously, the statements above refer to capabilities of at least one
projection of the selected object. The strength of gravitational lenses
increases when moving from type i) to type iii) since, e.g.,
the presence of a caustic does not imply a non-vanishing cross section,
and the bulk of cross section values is actually lower than 10-3 Mpc2 h-2 (see Paper I). The redshift distributions for these three categories of lensing clusters are shown in Fig. 1.
Mpc2 h-2.
Obviously, the statements above refer to capabilities of at least one
projection of the selected object. The strength of gravitational lenses
increases when moving from type i) to type iii) since, e.g.,
the presence of a caustic does not imply a non-vanishing cross section,
and the bulk of cross section values is actually lower than 10-3 Mpc2 h-2 (see Paper I). The redshift distributions for these three categories of lensing clusters are shown in Fig. 1.
The thick green curve in Fig. 1 represents the lensing efficiency
![]() ,
that we simply defined as the effective lensing distance normalized such as to have unit integral between
,
that we simply defined as the effective lensing distance normalized such as to have unit integral between
![]() and
and
![]() .
In other words, the lensing efficiency is defined as
.
In other words, the lensing efficiency is defined as
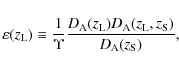
|
(4) |
where
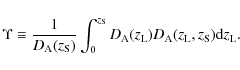
|
(5) |
Since the effective lensing distance defines the critical surface density, which is responsible for the formation of critical curves (Padmanabhan & Subramanian 1988; Subramanian & Cowling 1986), it is expected that the redshift trend of
![\begin{figure}
\par\includegraphics[width=12cm]{14962f2}
\vspace*{8mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg42.png)
|
Figure 2:
The correlation between the logarithm of the virial mass (
|
| Open with DEXTER | |
This is actually the case, with
![]() dropping to zero both at
dropping to zero both at
![]() and at
and at
![]() ,
as do the simulated distributions. However the redshift distributions
of strong lensing clusters are substantially more peaked than the
lensing efficiency defined above, and the latter displays a substantial
high-redshift tail that is absent in the former. This fact can be
understood recalling that the lensing efficiency does not contain any
information about the evolution of the cluster mass function. Massive
clusters are progressively rarer with increasing redshift, implying
that the redshift distribution of strong lensing clusters should also
experience an extra drop as compared to that due to pure geometric
suppression. This can be verified by additionally weighting the lensing
efficiency defined above with the number density of objects that at a
given redshift
,
as do the simulated distributions. However the redshift distributions
of strong lensing clusters are substantially more peaked than the
lensing efficiency defined above, and the latter displays a substantial
high-redshift tail that is absent in the former. This fact can be
understood recalling that the lensing efficiency does not contain any
information about the evolution of the cluster mass function. Massive
clusters are progressively rarer with increasing redshift, implying
that the redshift distribution of strong lensing clusters should also
experience an extra drop as compared to that due to pure geometric
suppression. This can be verified by additionally weighting the lensing
efficiency defined above with the number density of objects that at a
given redshift ![]() have mass larger than some fixed threshold value. This is shown by the dashed green curve in Fig. 1, where we adopted
have mass larger than some fixed threshold value. This is shown by the dashed green curve in Fig. 1, where we adopted
![]() h-1 as the lower mass limit. This roughly corresponds to the minimum mass of strong lensing clusters in the redshift range
h-1 as the lower mass limit. This roughly corresponds to the minimum mass of strong lensing clusters in the redshift range
![]() .
With this extra weighting the high-redshift tail of the simulated
distribution of strong lensing clusters is correctly captured, as
expected. There remain a disagreement at very low redshifts, due to the
fact that very close to the observer the minimum mass capable of
producing strong lensing grows rapidly well above
.
With this extra weighting the high-redshift tail of the simulated
distribution of strong lensing clusters is correctly captured, as
expected. There remain a disagreement at very low redshifts, due to the
fact that very close to the observer the minimum mass capable of
producing strong lensing grows rapidly well above
![]() h-1.
h-1.
Next, let us examine the differences between the redshift distributions
of the three categories of strong lensing clusters that we have
defined. Going from subsample i) to iii), that is increasing
the strength of lenses, we see that the distribution shrinks, with the
high-redshift tail being progressively removed and the height of the
intermediate-redshift bins increasing. This is an obvious consequence
of the fact that the more efficient cluster lenses are expected to be
found far away both from the observer and the source plane. As a
consequence, no clusters belonging to sample iii) are found beyond
![]() ,
while clusters merely producing critical lines extend up to
,
while clusters merely producing critical lines extend up to
![]() .
.
4 Results
4.1 Lensing efficiency scaling relations
4.1.1 Mass
As a next point we studied the correlation between the virial mass of galaxy clusters in the M AREN OSTRUM U NIVERSE
and their strong lensing efficiency, represented by the cross section
for giant arcs. As done before, since for each model cluster we
computed the cross section along three different (orthogonal)
projections, we quantify the lensing efficiency of each individual
cluster as the average
![]() over the three projections. In order to simplify the notation, we introduce two new variables,
over the three projections. In order to simplify the notation, we introduce two new variables,
![]() and
and
![]() .
.
![\begin{figure}
\par\includegraphics[width=12cm]{14962f3}
\vspace*{-2.5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg53.png)
|
Figure 3:
The distribution of the logarithm of cross sections for giant arcs (
|
| Open with DEXTER | |
In Fig. 2 we show the correlation between the variables x and y for the clusters of the M AREN OSTRUM U NIVERSE that are contained within various redshift snapshots. For each panel we also show the best linear fit, in the form
![]() .
We also tried a higher order fit to the points in Fig. 2,
but the result is not significantly different. We explicitly included
the lens redshift dependence of the two best fit parameters a and b,
since in general their value will differ for different simulation
snapshots. The redshift evolution of the best fit parameters is
discussed in Sect. 4.2. As
expected, an obvious correlation is present, with more massive objects
having on average the larger cross sections. The scatter on the
correlation is however considerably large, being up to one order of
magnitude both in mass and cross section. This scatter is due to the
combination of many different effects, including cluster ellipticity,
substructures, and alignment with the line of sight. We investigate
more on this scatter further below.
.
We also tried a higher order fit to the points in Fig. 2,
but the result is not significantly different. We explicitly included
the lens redshift dependence of the two best fit parameters a and b,
since in general their value will differ for different simulation
snapshots. The redshift evolution of the best fit parameters is
discussed in Sect. 4.2. As
expected, an obvious correlation is present, with more massive objects
having on average the larger cross sections. The scatter on the
correlation is however considerably large, being up to one order of
magnitude both in mass and cross section. This scatter is due to the
combination of many different effects, including cluster ellipticity,
substructures, and alignment with the line of sight. We investigate
more on this scatter further below.
In Fig. 2 we
also reported the expected trend with mass and redshift of the cross
section for giant arcs produced by a Singular Isothermal Sphere (SIS
henceforth) lens model acting on circular, point-like sources (see Narayan & Bartelmann 1999, for a thorough description of this simple lens model). For arcs with length-to-width ratio larger than R0, this cross section can be written as
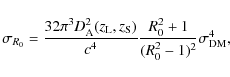
|
(6) |
where
In the previous equation we used
Despite the different normalizations, the slopes of the best fit x-y
relations and those derived for the SIS models are intriguingly similar
(despite the latter being slightly flatter), especially in light of the
large scatter displayed in Fig. 2.
This implies the interesting fact that, notwithstanding the spread that
is introduced in the cluster population by differences in individual
formation histories (mergers, substructures, ellipticity, etc.), the
simple ``self-similar'' scaling
![]() (where
(where ![]() is the Einstein radius of the lens) can be considered a fair representation of average strong lensing clusters.
is the Einstein radius of the lens) can be considered a fair representation of average strong lensing clusters.
As noted above the two parameters of the linear fit change with the
lens redshift, however we did not find any discernible trend, with both
the
![]() and
and
![]() functions being rather flat and oscillating around almost fixed values.
An exception to this is given by the very low or very high-redshift
snapshots, where the fluctuations become very large. However in those
snapshots very few cluster with non-vanishing cross sections are
available, hence the resulting fit is likely not to be trusted. We come
back to this issue again in Sect. 4.2.
functions being rather flat and oscillating around almost fixed values.
An exception to this is given by the very low or very high-redshift
snapshots, where the fluctuations become very large. However in those
snapshots very few cluster with non-vanishing cross sections are
available, hence the resulting fit is likely not to be trusted. We come
back to this issue again in Sect. 4.2.
![\begin{figure}
\par\includegraphics[width=12cm]{14962f4}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg66.png)
|
Figure 4:
The correlation between the logarithm of the cross section for giant arcs (
|
| Open with DEXTER | |
Since the scatter around the best fit relations in Fig. 2 is substantial, it is necessary to quantify it. Hence, for each strong lensing cluster present in each redshift snapshot we computed the quantity y-yx, where yx is the logarithm of the cross section given by the best fit relation at that redshift and for a fixed logarithmic mass, while y is the logarithm of the actual cross section. In Fig. 3 we show how, for each of the redshift snapshots shown in Fig. 2, these quantities are distributed.
![\begin{figure}
\par\includegraphics[width=12cm]{14962f5}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg68.png)
|
Figure 5:
The distribution of the logarithm of cross sections for giant arcs (
|
| Open with DEXTER | |
where H3(u) is the Hermite polynomial of third degree, that reads
| H3(u) = u3-3u. | (9) |
The parameter
In Fig. 3 the red solid curves show the results of this kind of non-Gaussian fit. As can be seen, Eq. (8)
provides a slight improvement over the simply Gaussian fit, especially
for low and high-redshift snapshots. It is likely that the fit could be
improved further by introducing a third free parameter (that in the
Edgeworth expansion would represent the normalized kurtosis). Also,
there are several snapshots (e.g., those at z = 0.56 and z
= 0.66) that are showing traces of bimodality, for which a fit with the
superposition of two curves would be preferable. As we discuss in
Sect. 4.2 the two parameter fits that are shown in Fig. 3 are not precise enough to accurately reproduce the strong lensing optical depth measured in the MARENOSTRUM SIMULATION.
Since however we have found that the inclusion of the scatter is not
necessary for this scope, we prefer to add no further complication and
stick to the two parameter fits. Besides, while the redshift evolution
of
![]() is rather flat around an average of
is rather flat around an average of ![]() 0.3, the redshift evolution of the parameter
0.3, the redshift evolution of the parameter
![]() is much more noisy than for
is much more noisy than for
![]() and
and
![]() ,
showing large fluctuations between neighboring redshift snapshots. This
fact suggests that with the introduction of the skewness as an
additional fit parameter we are in part overfitting the noise of
measured distributions. The addition of further parameters would worsen
this situation even more, thus being of little practical use.
,
showing large fluctuations between neighboring redshift snapshots. This
fact suggests that with the introduction of the skewness as an
additional fit parameter we are in part overfitting the noise of
measured distributions. The addition of further parameters would worsen
this situation even more, thus being of little practical use.
4.1.2 Luminosity
Since the M AREN OSTRUM U NIVERSE
simulation includes adiabatic gas, we could consider the correlations
of the virial mass and the strong lensing cross section with the
bolometric X-ray luminosity, the latter being a quantity that is more
directly related to observable features. To that end, we introduced a
new variable
![]() ,
where
,
where ![]() is the bolometric X-ray luminosity. In Fig. 4 we report the relation between y and
is the bolometric X-ray luminosity. In Fig. 4 we report the relation between y and ![]() ,
while the
,
while the ![]() relation has been already discussed in Paper I.
relation has been already discussed in Paper I.
In the same Figure we also report the best linear fit (red solid lines) and the ![]() relation that can be deduced by combining the SIS scaling derived above for the y-x
relation with self-similar arguments (green dashed lines), according to
the following line of reasoning. Let us assume that dark matter halos
in the M AREN OSTRUM U NIVERSE
simulation follow on average a NFW density profile. Self-similar
scaling arguments imply that the bolometric luminosity of a plasma in
hydrostatic equilibrium in the potential well of a dark matter halo
with such a density profile follows (Eke et al. 1998; Fedeli et al. 2007)
relation that can be deduced by combining the SIS scaling derived above for the y-x
relation with self-similar arguments (green dashed lines), according to
the following line of reasoning. Let us assume that dark matter halos
in the M AREN OSTRUM U NIVERSE
simulation follow on average a NFW density profile. Self-similar
scaling arguments imply that the bolometric luminosity of a plasma in
hydrostatic equilibrium in the potential well of a dark matter halo
with such a density profile follows (Eke et al. 1998; Fedeli et al. 2007)
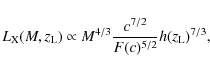
|
(10) |
where
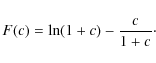
|
(11) |
Since even for the most massive clusters the concentration is at least of a few, we have that
|
(12) |
In order to fix the normalization we simply required that the bolometric X-ray luminosity and cross sections of the most luminous cluster in the simulation are reproduced. We would like to stress that the procedure we followed for deriving of the above scaling relations is likely oversimplified. Here we did not want to perform a completely rigorous derivation, just to make the case for the fact that simple scaling arguments can produce correlations that are rather similar in slope to those observed in the M AREN OSTRUM U NIVERSE.
Because of the increase in average X-ray luminosity with increasing mass and because of the trend reported in Fig. 2, it is expected that the lensing cross section also increases with the X-ray emission. This is indeed observed in Fig. 4 and the correlation is visibly tighter than the y-x correlation. In order to better appreciate this, in Fig. 5
we report the distribution of logarithmic cross sections around the
best fit relation for a fixed X-ray luminosity. As a matter of fact,
the logarithmic slope of the ![]() relation is relatively similar to that of the y-x relation (in agreement with the self-similar scaling detailed above), but the scatter around the latter is systematically
relation is relatively similar to that of the y-x relation (in agreement with the self-similar scaling detailed above), but the scatter around the latter is systematically ![]() 25%
smaller than around the former. Also, as we already found for the
mass-cross section relation, the introduction of a non-Gaussian part to
the functional form used for fitting the distribution around the best
suitable luminosity-cross section relation does not substantially alter
the fit with respect to the perfectly Gaussian form.
25%
smaller than around the former. Also, as we already found for the
mass-cross section relation, the introduction of a non-Gaussian part to
the functional form used for fitting the distribution around the best
suitable luminosity-cross section relation does not substantially alter
the fit with respect to the perfectly Gaussian form.
![\begin{figure}
\par\mbox{ \includegraphics[width=8cm]{14962f6a} \includegraphics[width=8cm]{14962f6b} }\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg86.png)
|
Figure 6: Left panel. The differential optical depth for giant arcs obtained by all clusters in the M AREN OSTRUM U NIVERSE as a function of lens redshift (black solid line). The red dashed line represents the synthetic differential optical depth obtained with the procedure outlined in the text (q=3.5), while the shaded area represents the effect of a 30% uncertainty on the minimum mass at the pivotal redshift (see the text for details). Right panel. Same as the left panel but with the blue and green dashed lines now representing the synthetic optical depths computed with values of q different from 3.5, as labeled. |
| Open with DEXTER | |
The fact that the scatter around the best fit relation is decreased suggests that there should be a more fundamental relation of the cross section for giant arcs with the bolometric X-ray luminosity, rather than with the virial mass. This can be somewhat expected from several qualitative considerations: a) relaxed clusters are expected to have large gas and dark matter central densities. This would increase both the X-ray emissivity, that is proportional to the square of the gas density, and the extension of the critical curves (Fedeli et al. 2007); b) cluster mergers are expected to compress and heat up the intracluster medium, hence increasing the X-ray luminosity. At the same time, interactions should increase the convergence and shear fields of the cluster (Torri et al. 2004), thus enhancing its lensing efficiency; c) in general, the X-ray luminosity is particularly sensitive to the physical processes taking place in the inner region of galaxy clusters, and so is the strong lensing efficiency. The virial mass on the other hand is much less sensitive to that. This also implies that the correlation between the lensing cross section and the mass contained within smaller radii (e.g., M500 M2500, etc.), should be tighter than with the virial mass.
A closer inspection of Fig. 4 shows that virtually all the clusters expected to have at least one giant arc (
![]() Mpc2 h-2) have a bolometric X-ray luminosity that is larger than
Mpc2 h-2) have a bolometric X-ray luminosity that is larger than ![]()
![]() erg s-1.
The converse is in general not true, in the sense that many clusters
exist with a high luminosity that make rather poor strong lenses.
Hence, strong lensing clusters would be good tracers of centrally dense
intra-cluster medium, while the converse would not hold in general.
erg s-1.
The converse is in general not true, in the sense that many clusters
exist with a high luminosity that make rather poor strong lenses.
Hence, strong lensing clusters would be good tracers of centrally dense
intra-cluster medium, while the converse would not hold in general.
Finally, we tried to recompute the scaling relations between x and ![]() and the logarithm of the cross section y by taking into account only relaxed clusters. Relaxation was quantified through the parameter
and the logarithm of the cross section y by taking into account only relaxed clusters. Relaxation was quantified through the parameter ![]() introduced in Paper I, that expresses deviations from virial equilibrium: negative
introduced in Paper I, that expresses deviations from virial equilibrium: negative ![]() implies systems dominated by the kinetic energy, positive
implies systems dominated by the kinetic energy, positive ![]() by the potential energy, while
by the potential energy, while ![]() implies perfect virial equilibrium. We recomputed the above scaling relations by using only clusters with
implies perfect virial equilibrium. We recomputed the above scaling relations by using only clusters with
![]() ,
and found no reduction in the scatter about the best fit x-y and
,
and found no reduction in the scatter about the best fit x-y and ![]() relations, nor a significant shift of the quartiles of the
distributions. What happen instead is just a removal of the highest
mass/luminosity objects, which is expected since those are the least
relaxed on average. This is an indication that, intriguingly, the bulk
of this scatter should not be originated by the dynamical activity of
clusters, rather by triaxiality and concentration distributions. The
latter, particularly,
is expected to have a major impact since the cross section is
remarkably sensitive to it, and the concentration itself has a
substantial intrinsic scatter. Because of the relatively low resolution
of clusters in the simulation, we could compute only concentrations for
staked cluster samples, not for individual objects. Hence we could not
asses this issue in detail.
relations, nor a significant shift of the quartiles of the
distributions. What happen instead is just a removal of the highest
mass/luminosity objects, which is expected since those are the least
relaxed on average. This is an indication that, intriguingly, the bulk
of this scatter should not be originated by the dynamical activity of
clusters, rather by triaxiality and concentration distributions. The
latter, particularly,
is expected to have a major impact since the cross section is
remarkably sensitive to it, and the concentration itself has a
substantial intrinsic scatter. Because of the relatively low resolution
of clusters in the simulation, we could compute only concentrations for
staked cluster samples, not for individual objects. Hence we could not
asses this issue in detail.
4.2 Optical depths
4.2.1 Synthetic optical depth
In Fig. 6 we show the
differential optical depth as a function of lens redshift. The
differential optical depth is the integrand of Eq. (2),
and represents the contribution to the total optical depth that is
given by structures at different lens redshifts. As a consequence, the
integral under the black solid curve in Fig. 6 represents the total optical depth, that for sources at
![]() amount to
amount to
![]() .
The differential optical depth has the generic shape that is expected,
namely dropping at low and high redshift due to the geometric
suppression of the lensing efficiency. The total optical depth is
substantially lower than that reported for a
.
The differential optical depth has the generic shape that is expected,
namely dropping at low and high redshift due to the geometric
suppression of the lensing efficiency. The total optical depth is
substantially lower than that reported for a
![]() cosmology in Fedeli et al. (2008),
which is to be expected since there the authors used a complete source
redshift distribution, while here we adopted sources at a fixed
redshift. By multiplying the total optical depth with the number counts
of source galaxies at
cosmology in Fedeli et al. (2008),
which is to be expected since there the authors used a complete source
redshift distribution, while here we adopted sources at a fixed
redshift. By multiplying the total optical depth with the number counts
of source galaxies at
![]() it is possible to infer the abundance of arcs produced by those sources
that are visible below some given magnitude threshold (see the
discussion is Sect. 2).
it is possible to infer the abundance of arcs produced by those sources
that are visible below some given magnitude threshold (see the
discussion is Sect. 2).
The existence of a relation between the virial mass of galaxy clusters and their cross sections for giant arcs (Sect. 4.1) implies that we could in principle construct a synthetic realization of the optical depth in the following way. For each step in redshift we randomly extract a large number of masses, associate a cross section to each mass through the x-y relation described above, suitably randomized according to the scatter around the best fit relation, and use these cross sections for computing the differential optical depth at the fixed redshift. This kind of procedure would allow one to compute strong lensing optical depths based only on the scaling relations that we have found and without expensive calculations involving ray-tracing simulations and cross section evaluations.
In Fig. 7 we show the redshift evolution of the parameters
![]() and
and
![]() defined in the previous Sect. 4.1.
As announced, both of them oscillate around a roughly constant value.
We plot in the same Figure also the average values, computed over the
redshift range [0.1,1.1], since outside this range very little lensing
clusters are present per redshift snapshot, and the result of the
fitting procedure is less reliable. These two average values amount to
defined in the previous Sect. 4.1.
As announced, both of them oscillate around a roughly constant value.
We plot in the same Figure also the average values, computed over the
redshift range [0.1,1.1], since outside this range very little lensing
clusters are present per redshift snapshot, and the result of the
fitting procedure is less reliable. These two average values amount to
![]() and
and
![]() .
Although the procedure described above would make use of the specific vales
.
Although the procedure described above would make use of the specific vales
![]() and
and
![]() at each redshift
at each redshift ![]() ,
this would not be of very practical use. Therefore we decided to adopt the same values of the two parameters
,
this would not be of very practical use. Therefore we decided to adopt the same values of the two parameters ![]() and
and ![]() at each redshift snapshot, equal to the respective average values. At first, we tried to ignore the scatter around the best fit y-x
relation, i.e., we assigned at each mass the exact value that is
prescribed by the linear logarithmic fit with the redshift averaged
values. Another factor that needs to be taken into account is the
smallest mass
at each redshift snapshot, equal to the respective average values. At first, we tried to ignore the scatter around the best fit y-x
relation, i.e., we assigned at each mass the exact value that is
prescribed by the linear logarithmic fit with the redshift averaged
values. Another factor that needs to be taken into account is the
smallest mass
![]() that, at each redshift step, enters in the computation of the differential optical depth (M1 in Eq. (2)).
As it turns out this point is of fundamental importance, since the
optical depth tends to be dominated by the smallest clusters capable of
producing a non-vanishing cross section, being by far the more
abundant. Instead of adopting as such lower limit the smallest mass
that at each redshift produces a non-vanishing cross section in the M AREN OSTRUM U NIVERSE we let the redshift evolution of
that, at each redshift step, enters in the computation of the differential optical depth (M1 in Eq. (2)).
As it turns out this point is of fundamental importance, since the
optical depth tends to be dominated by the smallest clusters capable of
producing a non-vanishing cross section, being by far the more
abundant. Instead of adopting as such lower limit the smallest mass
that at each redshift produces a non-vanishing cross section in the M AREN OSTRUM U NIVERSE we let the redshift evolution of
![]() be
be
We adopted this procedure for a twofold reason. Firstly, choosing a different minimum mass at each redshift snapshot is not practical, exactly as it was not practical to use a different pair of best fitting parameters at each redshift. Second, it is likely that this minimum mass is siumlation-dependent, or in different words, that rerunning the same simulation several times would produce a distribution of minimum masses at a given redshift, due to the randomness of the cluster formation histories.
![\begin{figure}
\par\includegraphics[width=8.5cm]{14962f7}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg99.png)
|
Figure 7: The redshift evolution of the two parameters defining the best fit x-y relation (see the text for details), with the respective standard errors. The black and red solid horizontal lines represent the respective redshift averages, while the green horizontal line represents the slope expected for a SIS lens model. |
| Open with DEXTER | |
In Eq. (13) the function
![]() is the lensing efficiency that has been introduced in Sect. 3,
is the lensing efficiency that has been introduced in Sect. 3,
![]() is some pivotal lens redshift and
is some pivotal lens redshift and
![]() is the corresponding minimum lensing mass. We adopted as pivotal the
redshift at which the differential optical depth is maximal,
is the corresponding minimum lensing mass. We adopted as pivotal the
redshift at which the differential optical depth is maximal,
![]() ,
that also coincides with the broad maximum in the lensing efficiency reported in Fig. 1. At this redshift the smallest mass with non-vanishing cross section is
,
that also coincides with the broad maximum in the lensing efficiency reported in Fig. 1. At this redshift the smallest mass with non-vanishing cross section is
![]() .
Ideally, selecting a suitable value of q
for each lens redshift would allow to match the synthetic optical
depth, since one would encapsulate in this free parameter all the
remaining uncertainty that has not been taken into account, i.e., the
deviation of the parameters
.
Ideally, selecting a suitable value of q
for each lens redshift would allow to match the synthetic optical
depth, since one would encapsulate in this free parameter all the
remaining uncertainty that has not been taken into account, i.e., the
deviation of the parameters
![]() and
and
![]() from their redshift averages, the scatter around the best fit x-y relation, etc. In practice, we can choose a single value of q that gives an overall good fit to the true optical depth.
from their redshift averages, the scatter around the best fit x-y relation, etc. In practice, we can choose a single value of q that gives an overall good fit to the true optical depth.
The ``synthetic'' optical depth resulting from this procedure is represented in Fig. 6, together with the effect of allowing some uncertainty on the value of
![]() and changing q within some reasonable interval. The deviation of the synthetic optical depth from the true one for, e.g., q = 3.5 might seem quite significant. Particularly, the true optical depth appears to be quite overestimated at
and changing q within some reasonable interval. The deviation of the synthetic optical depth from the true one for, e.g., q = 3.5 might seem quite significant. Particularly, the true optical depth appears to be quite overestimated at
![]() due to the fact that both the parameters
due to the fact that both the parameters
![]() and
and
![]() are below the average at those redshifts (see Fig. 7).
However it should be recalled that the Figure has logarithmic scale,
and as a matter of fact the synthetic optical depth with q = 3.5 differs from the true one only by about
are below the average at those redshifts (see Fig. 7).
However it should be recalled that the Figure has logarithmic scale,
and as a matter of fact the synthetic optical depth with q = 3.5 differs from the true one only by about ![]() 10-15%,
which is a truly negligible amount given the large uncertainties
involved in the estimation of arc abundances. Increasing the value of q to, e.g., 4.5 reduces the discrepancy on the total optical depth to only
10-15%,
which is a truly negligible amount given the large uncertainties
involved in the estimation of arc abundances. Increasing the value of q to, e.g., 4.5 reduces the discrepancy on the total optical depth to only ![]() 5%,
however in this case the high-redshift tail of the differential optical
depth is rather underestimated. Based on these numbers and in Fig. 6 we suggest to adopt a value of
5%,
however in this case the high-redshift tail of the differential optical
depth is rather underestimated. Based on these numbers and in Fig. 6 we suggest to adopt a value of
![]() as a fair compromise.
as a fair compromise.
Also shown in Fig. 6 is the effect of uncertainty in the value of
![]() .
As a matter of fact, a substantial fluctuation on the minimum lensing
mass at redshifts close to the pivotal one is found, due to the fact
that in such a boundary situation small variations in the internal
structure of the lens are enough to scatter the lens itself above or
below the threshold for cross section production. In Fig. 6 we show as an example the effect of a 30% uncertainty on
.
As a matter of fact, a substantial fluctuation on the minimum lensing
mass at redshifts close to the pivotal one is found, due to the fact
that in such a boundary situation small variations in the internal
structure of the lens are enough to scatter the lens itself above or
below the threshold for cross section production. In Fig. 6 we show as an example the effect of a 30% uncertainty on
![]() ,
which can easily shift the total optical depth of
,
which can easily shift the total optical depth of ![]() 50%. The effect of changing the value of q within a reasonable interval is relatively similar in amplitude to the effect of
50%. The effect of changing the value of q within a reasonable interval is relatively similar in amplitude to the effect of
![]() fluctuations.
fluctuations.
We have to observe that the reasonable way in which the synthetic
optical depth approximates the true one is heavily dependent on the
values of ![]() and
and ![]() that we assume. Particularly, to produce variations to the synthetic
optical depth with magnitude similar to that reported in the left panel
of Fig. 6,
it is sufficient to modify the normalization or the slope of the
mass-cross section relation at the percent level. This is way smaller
than the fluctuations and errors that are reported in Fig. 7.
For instance, adopting the slope of the mass-cross section relation
that is found for SIS lens model, instead of the redshift average that
we adopted, would produce a gross underestimate of the true optical
depth. This argument can be turned around by saying that the synthetic
optical depth is a fair representation of the true one only if the
normalization and the slope of the mass-cross section relation adopted
stay very close to their redshift-average values computed here.
that we assume. Particularly, to produce variations to the synthetic
optical depth with magnitude similar to that reported in the left panel
of Fig. 6,
it is sufficient to modify the normalization or the slope of the
mass-cross section relation at the percent level. This is way smaller
than the fluctuations and errors that are reported in Fig. 7.
For instance, adopting the slope of the mass-cross section relation
that is found for SIS lens model, instead of the redshift average that
we adopted, would produce a gross underestimate of the true optical
depth. This argument can be turned around by saying that the synthetic
optical depth is a fair representation of the true one only if the
normalization and the slope of the mass-cross section relation adopted
stay very close to their redshift-average values computed here.
![\begin{figure}
\par\includegraphics[width=12cm]{14962f8}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg106.png)
|
Figure 8: The difference between the true distribution around the best fit mass-cross section relation and the best Gaussian (blue shaded histograms with black contours) and non-Gaussian (magenta shaded histograms) fits. Results for several different redshift snapshots are shown, as labeled in the plot. |
| Open with DEXTER | |
Lastly, we would like to comment on the fact that in the above procedure for computing synthetic optical depth we neglected the role of the scatter around the best fit y-x relation. As we mentioned in Sect. 4.1, the fits that we performed to the distributions of y-yx both with a Gaussian and a non-Gaussian functions are not precise enough for the purpose of increasing the precision of the synthetic optical depth. This can be understood as follows: as it appears evident from a close inspection of Fig. 3, neither the Gaussian nor the non-Gaussian functional forms fully appreciate the asymmetry in the scatter of cross sections around the best fit. Namely, the distributions of y-yx tend to be substantially skewed toward negative values as compared to the best fits. As a consequence, the introduction of the scatter around the best fit actually worsen the agreement of the synthetic optical depth to the true one. This fact can be better appreciated by analyzing Fig. 8. There, the scatter around the best fit mass-cross section relation is shown once the best Gaussian and non-Gaussian fits were removed. It is obvious that the best Gaussian fit is substantially more positively skewed with respect to the true distribution, especially at high redshift. The same remains true for the non-Gaussian fit, although to a lesser extent. This means that, including the scatter in the computation of the synthetic optical depth effectively equals at assigning higher cross sections to a given mass with respect to reality. As a result the synthetic optical depth tends to be a substantial overestimate of the true one if the scatter is included
In order to solve this, a better fit to the distributions of y-yx
would be required, maybe with the superposition of two curves. This
however would increase the number of free parameters from two to four
at least. We chose not to pursue this route, since it would add
substantial complication to a model that already works quite
acceptably. As a matter of fact, given the very simplistic nature of
the underlying assumptions (one best fit relation valid for all
redshifts, absence of scatter, etc.) it is very remarkable that the
true optical depth can be reproduced at this level with just one
adjustable parameter, q. This very simple model for computing
synthetic optical depths can be very helpful for, e.g., evaluate the
contribution to arc abundance that is given by structures in various
redshift ranges without performing any actual strong lensing
calculation. Summarizing, in evaluating synthetic optical depths for
sources at
![]() we suggest to stick to the precise values of
we suggest to stick to the precise values of ![]() and
and ![]() that we adopted, and to use a value of q between 3.5 and 4.5, with the threshold mass at the pivot redshift equaling
that we adopted, and to use a value of q between 3.5 and 4.5, with the threshold mass at the pivot redshift equaling
![]() h-1.
h-1.
4.2.2 The role of dynamical activity
In Fig. 9 we show the differential optical depth of the M AREN OSTRUM U NIVERSE
obtained by excising those clusters that are not relaxed enough. The
relaxation of a cluster was established via the virial equilibrium
parameter, defined in Paper I (see also Shaw et al. 2006). As can be seen the exclusion of clusters with a value of ![]() significantly different from zero causes an erosion of the
high-redshift tail of the differential optical depth. Particularly,
when only clusters with
significantly different from zero causes an erosion of the
high-redshift tail of the differential optical depth. Particularly,
when only clusters with
![]() are included, the differential optical depth peaks at
are included, the differential optical depth peaks at
![]() instead of
instead of
![]() ,
and the total optical depth is reduced by a factor of 2. In other
words, half of the number of giant arcs produced by sources at
,
and the total optical depth is reduced by a factor of 2. In other
words, half of the number of giant arcs produced by sources at
![]() are expected to be found inside clusters that are substantially
unrelaxed. A significant contribution to arc statistics from clusters
at
are expected to be found inside clusters that are substantially
unrelaxed. A significant contribution to arc statistics from clusters
at
![]() can be expected only by including objects with
can be expected only by including objects with
![]() .
.
This trend of the optical depth with the virial equilibrium of clusters
can be easily understood by looking at the redshift evolution of ![]() that has been presented in Paper I. Namely, while at
that has been presented in Paper I. Namely, while at ![]() the average
the average ![]() is quite close to zero, at high redshifts it tends to become strongly negative. This means that, removing clusters with
is quite close to zero, at high redshifts it tends to become strongly negative. This means that, removing clusters with ![]() very different from zero is equivalent at removing high-redshift
clusters, and hence the drop in the differential optical depth at large
very different from zero is equivalent at removing high-redshift
clusters, and hence the drop in the differential optical depth at large
![]() follows. Intriguingly, the redshift distribution of strong lensing
clusters carries information on the dynamical state of the deflectors:
selecting clusters that are capable of producing giant gravitational
arcs at
follows. Intriguingly, the redshift distribution of strong lensing
clusters carries information on the dynamical state of the deflectors:
selecting clusters that are capable of producing giant gravitational
arcs at
![]() we are automatically selecting objects that are relatively close to the
virial equilibrium. Vice versa, lensing clusters at high redshift are
very likely to be dynamically active.
we are automatically selecting objects that are relatively close to the
virial equilibrium. Vice versa, lensing clusters at high redshift are
very likely to be dynamically active.
![\begin{figure}
\par\includegraphics[width=9cm]{14962f9}\hfill\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg115.png)
|
Figure 9:
The differential optical depth in the M AREN OSTRUM U NIVERSE computed for all clusters in the simulation (black solid line) and by including only those clusters whose |
| Open with DEXTER | |
We wish to interpret this result in light of the incidence of gravitational arcs in high-redshift clusters found by, e.g., Gladders et al. (2003) (see also Zaritsky & Gonzalez 2003). Particularly, Gladders et al. (2003) analyzed the Red-sequence Cluster Survey (RCS, Gladders & Yee 2001), finding eight clusters at
![]() with
prominent gravitational arcs, for a total of 11 strong lensing
features, including tentative detections. By using Fig. 9 we can estimate that
with
prominent gravitational arcs, for a total of 11 strong lensing
features, including tentative detections. By using Fig. 9 we can estimate that ![]() 77% of the optical depth at
77% of the optical depth at
![]() is produced by clusters with
is produced by clusters with
![]() ,
which effectively means
,
which effectively means
![]() since the values of
since the values of ![]() are prominently negative, especially at high redshift (see Paper I). Thus, it is expected that
are prominently negative, especially at high redshift (see Paper I). Thus, it is expected that ![]() 8-9 of the 11 giant arcs of Gladders et al. (2003) are produced by substantially unrelaxed clusters. As a matter of fact, Gladders et al. (2003)
themselves argued that the high-redshift lensing clusters they found
are somewhat enhanced in their lensing efficiency by some physical
process, possibly the presence of substructures and dynamical activity.
8-9 of the 11 giant arcs of Gladders et al. (2003) are produced by substantially unrelaxed clusters. As a matter of fact, Gladders et al. (2003)
themselves argued that the high-redshift lensing clusters they found
are somewhat enhanced in their lensing efficiency by some physical
process, possibly the presence of substructures and dynamical activity.
Browsing the literature in order to confirm the fraction of strong lensing clusters that are dynamically unrelaxed gives inconclusive results. For instance, RCS 2319.9+0038 is part of a supercluster and is likely to be unrelaxed, as well as RCS 2156.7-0448 (Hicks et al. 2008). RCS 1620.2+2929 was shown by Gilbank et al. (2007) to have an excess velocity dispersion compared to what would be expected by its optical richness (Yee & Ellingson 2003), suggesting signs of dynamical activity. On the other hand, RCS 0224.5-0002 is likely a relaxed object (Hicks et al. 2007), totaling to 4 giant arcs found in dynamically active clusters versus 2 found in relaxed clusters. All the other RCS clusters used by Gladders et al. (2003) do not have information about the dynamical state. Obviously we are not able to draw any conclusion from this, but just want to stress that further study of the dynamical activity of strong lensing clusters, especially at high redshift, would be valuable in order to better characterize the cluster lens population.
4.2.3 X-ray selection effects
It is finally interesting to investigate how the optical depth
changes if clusters are selected with X-ray luminosity. This is
particularly worthy since past observational arc statistics studies
focused mainly on X-ray selected clusters (Gioia & Luppino 1994; Le Fevre et al. 1994; Luppino et al. 1999). In Fig. 10
we show the fraction of the total optical depth for giant arcs that is
contributed by clusters with luminosity above a given threshold. Under
the assumption that all sources lie at
![]() this corresponds to the fraction of gravitational arcs that are found
inside luminous clusters. Two lines are shown in Fig. 10, one referring to the bolometric X-ray luminosity (labeled
this corresponds to the fraction of gravitational arcs that are found
inside luminous clusters. Two lines are shown in Fig. 10, one referring to the bolometric X-ray luminosity (labeled ![]() ), the other to the luminosity computed in the [0.5,2] keV energy band (labeled
), the other to the luminosity computed in the [0.5,2] keV energy band (labeled ![]() ). The latter was estimated from the integrated luminosity by using the bolometric correction of Borgani et al. (1999).
For that we needed the global cluster temperature, which we estimated
from the redshift and the virial mass of the object by using the virial
relation
). The latter was estimated from the integrated luminosity by using the bolometric correction of Borgani et al. (1999).
For that we needed the global cluster temperature, which we estimated
from the redshift and the virial mass of the object by using the virial
relation
![\begin{displaymath}kT = \frac{1.38~{\rm keV}}{\gamma}\left(\frac{M}{10^{15}~M_\o...
...rm m},0} \Delta_{\rm v}(z_{\rm L}) \right]^{1/3}(1+z_{\rm L}),
\end{displaymath}](/articles/aa/full_html/2010/11/aa14962-10/img120.png)
|
(14) |
where
Since no clusters with
![]() erg s-1 have non-vanishing cross section (see Fig. 4),
the totality of the strong lensing optical depth is produced by
clusters with bolometric luminosity above that value, as can be seen in
Fig. 10. In other words, if one considers a complete cluster sample containing all the objects with
erg s-1 have non-vanishing cross section (see Fig. 4),
the totality of the strong lensing optical depth is produced by
clusters with bolometric luminosity above that value, as can be seen in
Fig. 10. In other words, if one considers a complete cluster sample containing all the objects with
![]() erg s-1, then this sample would include all the strong lensing clusters in the surveyed area. While several clusters with
erg s-1, then this sample would include all the strong lensing clusters in the surveyed area. While several clusters with
![]() erg s-1
exist, their contribution to the total optical depth is small, since
they are likely to be very massive and hence extremely rare. As a
matter of fact, Fig. 10 shows that such objects contribute only
erg s-1
exist, their contribution to the total optical depth is small, since
they are likely to be very massive and hence extremely rare. As a
matter of fact, Fig. 10 shows that such objects contribute only ![]() 20% of the total giant arc abundance. If one considers the band luminosity, clusters with
20% of the total giant arc abundance. If one considers the band luminosity, clusters with
![]() erg s-1
also contribute more than 90% of the total arc abundance. However,
the drop of the optical depth with luminosity is somewhat steeper than
before, with clusters having
erg s-1
also contribute more than 90% of the total arc abundance. However,
the drop of the optical depth with luminosity is somewhat steeper than
before, with clusters having
![]() erg s-1 contributing only
erg s-1 contributing only ![]() 20% to the total optical depth.
20% to the total optical depth.
These results are particularly relevant in order to establish the
reliability of observational studies directed toward arc statistics. As
a classic example (and without the pretense of being rigorous), we
considered the work of Le Fevre et al. (1994),
where the authors performed a search for giant arcs inside clusters
extracted from the Einstein Medium Sensitivity Survey (EMSS, Gioia & Luppino 1994) by having luminosities in the [0.3,3.5] keV energy band larger than
![]() erg s-1.
Although we did not compute the luminosities in that energy band for
all of our simulated clusters , the relative result will lie somewhere
in between the red and black lines in Fig. 10, implying that at least
erg s-1.
Although we did not compute the luminosities in that energy band for
all of our simulated clusters , the relative result will lie somewhere
in between the red and black lines in Fig. 10, implying that at least ![]() 20%
of the arcs were missed in that sample. We estimated the true
luminosity in the [0.3,3.5] keV energy band only for a subsample
of the M AREN OSTRUM U NIVERSE lensing clusters, and found that this fraction should be about
20%
of the arcs were missed in that sample. We estimated the true
luminosity in the [0.3,3.5] keV energy band only for a subsample
of the M AREN OSTRUM U NIVERSE lensing clusters, and found that this fraction should be about ![]() .
Hence, these observational estimates of arc abundances would have to be
corrected for this factor, thus worsening the disagreement with
theoretical estimates (Fedeli et al. 2008).
Nevertheless, such a correction is likely to be small compared to other
uncertainties concerning theoretical and observational estimates of
arc statistics.
.
Hence, these observational estimates of arc abundances would have to be
corrected for this factor, thus worsening the disagreement with
theoretical estimates (Fedeli et al. 2008).
Nevertheless, such a correction is likely to be small compared to other
uncertainties concerning theoretical and observational estimates of
arc statistics.
![\begin{figure}
\par\includegraphics[width=9cm]{14962f10}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg131.png)
|
Figure 10:
The fraction of the total optical depth that is contributed by clusters of the M AREN OSTRUM U NIVERSE with logarithm of the bolometric X-ray luminosity (in units of 1044 erg s-1,
|
| Open with DEXTER | |
This kind of study is somewhat similar to the analysis performed in Fedeli & Bartelmann (2007), where the semi-analytic optical depth actually observed in flux limited X-ray cluster samples was detailed. However, the two works cannot be directly compared because there a full account for instrumental effects was presented that is missing here and a different plasma model is used (Raymond & Smith 1977).
5 Summary and discussion
In this work we investigated the optical depth emerging from the strong
lensing properties of a very large set of numerical galaxy clusters
extracted from the M AREN OSTRUM U NIVERSE cosmological simulation. The simulation has the same boxsize of the MILLENNIUM run (Springel 2005),
and includes an equal number of particles for both dark matter and
adiabatic gas. The cosmological parameters used in the simulation are
in agreement with the WMAP-1 year data release, and in particular
the normalisation of the matter power spectrum is
![]() .
Although this is higher than the results of the WMAP-5 year data analysis (Komatsu et al. 2009, see also Komatsu et al. 2010),
the two are still consistent at 95% Confidence Level.
Additionally, studies of the present abundance of X-ray clusters
indicate a somewhat higher normalization than found by the WMAP team (Yepes et al. 2007; Wojtak & Lokas 2010; Wen et al. 2010).
.
Although this is higher than the results of the WMAP-5 year data analysis (Komatsu et al. 2009, see also Komatsu et al. 2010),
the two are still consistent at 95% Confidence Level.
Additionally, studies of the present abundance of X-ray clusters
indicate a somewhat higher normalization than found by the WMAP team (Yepes et al. 2007; Wojtak & Lokas 2010; Wen et al. 2010).
Either way, a lower normalization of the matter power spectrum would imply a later formation of cosmic structure, with consequent lower abundance of massive galaxy clusters and a lower average concentration thereof. Both of these effects would act to reduce the optical depth (Fedeli et al. 2008), however, we expect the relative contributions to the arc abundance given by unrelaxed/luminous clusters to be mildly affected. Additionally, a lower dark matter halo concentration might be compensated by the introduction of gas cooling, that would increase the amount of mass flowing to the central region of galaxy clusters.
Before summing up, there is one point of our analysis that we would like to stress. The population of simulated dark matter halos capable of producing giant arcs has a lower mass limit due to the fact that when caustic curves become too small compared to the average source size, the related images can only very rarely be strongly distorted. For this reason isolated massive galaxies, that yet can produce arcs in particularly favorable circumstances, did not enter in the computation of the optical depths. Similarly, the simulation cannot realistically account for the formation of individual galaxies inside clusters due to the lack of baryon cooling, and therefore giant arcs that are mainly produced by those galaxies are also not included in our computations. However we argue for the influence of these issues on the optical depths to be small, since the effect of individual galaxies on the strong lensing cross sections of clusters has already been estimated (Meneghetti et al. 2000; Wambsganss et al. 2008) to be mild, and the probability of isolated galaxies for producing giant arcs is much too small for it being compensated by their larger abundance. Besides, real strong cluster lensing observations do not focus, by definition, on lensing by isolated galaxies. Nevertheless, the aforementioned limitations of our analysis are to be kept in mind.
The main conclusions that we reached in this paper can be summarized as follows.
- We quantified the correlation between the virial mass of
galaxy clusters and the cross section for giant arcs. This relation is
approximately linear in logarithm with a slope around
 1.5
and accounts for the expected fact that more massive objects have an
higher probability of producing strong lensing events. The parameters
of the best fit are roughly constant with redshift, although
significant oscillations around the mean are displayed.
1.5
and accounts for the expected fact that more massive objects have an
higher probability of producing strong lensing events. The parameters
of the best fit are roughly constant with redshift, although
significant oscillations around the mean are displayed.
- A similar correlation (with a similar slope) was found between the bolometric X-ray luminosity and the lensing efficiency. This correlation appears to the tighter than the previous one, reflecting the fact that both X-ray emissivity and lensing cross sections are particularly sensitive to the processes occurring at the very center of galaxy clusters.
- Both the correlations described above display a substantial scatter. In particular, the scatter around the best fit mass-cross section relation can be up to one order of magnitude. We found that the distributions around the best fit logarithmic relations are approximately Gaussian, although significant deviations from Gaussianity might be found.
- Using the best fit correlations between mass and lensing efficiency we managed to construct a synthetic optical depth that with only one adjustable parameter manages to reproduce acceptably well the true differential optical depth.
- We computed the contribution to the total optical depth that is given by relaxed and unrelaxed structures, where relaxation was defined as deviation from virial equilibrium. We found that unrelaxed structures mainly contribute to the high-redshift part of the optical depth, in agreement with the standard paradigm for structure formation.
- Similarly, we evaluated the contribution to the total arc abundance given by structures of various X-ray luminosity, thus quantifying the bias present in arc statistic studies based on X-ray selected clusters.
We believe the large set of strong lensing cross sections computed in this work to have a wide range of future applications beyond those exploited here and in Paper I, since it covers an abundant sample of realistically simulated galaxy clusters. We are currently planning to use cluster observables like the X-ray luminosity to construct realistic past light cones, in order to better evaluate possible selection effects and to better compare the lens population to the overall cluster population.
AcknowledgementsPart of this work has been performed under the Project HPC-EUROPA (RII3-CT-2003-506079), with the support of the European Community - Research Infrastructure Action under the FP6 ``Structuring the European Research Area'' Programme. We acknowledge financial contributions from contracts ASI-INAF I/023/05/0, ASI-INAF I/088/06/0 and ASI ``EUCLID-DUNE'' I/064/08/0. We warmly thank F. Pace for help in performing the strong lensing analysis and M. Roncarelli for aid in the computation of X-ray luminosities. We additionally would like to acknowledge M. Bartelmann and L. Moscardini for insightful discussions on the manuscript. The M AREN OSTRUM U NIVERSE simulation has been done at BSC-CNS (Spain) and analyzed at NIC Jülich (Germany). G.Y. acknowledges support of MICINN (Spain) through research grants FPA2009-08958 and AYA2009-13875-C03-02. We are grateful to an anonymous referee for comments that helped improving the presentation of our work.
References
- Bartelmann, M., Huss, A., Colberg, J., Jenkins, A., & Pearce, F. 1998, A&A, 330, 1 [NASA ADS] [Google Scholar]
- Bartelmann, M., Meneghetti, M., Perrotta, F., Baccigalupi, C., & Moscardini, L. 2003, A&A, 409, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Blinnikov, S., & Moessner, R. 1998, A&AS, 130, 193 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Borgani, S., Rosati, P., Tozzi, P., & Norman, C. 1999, ApJ, 517, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Navarro, J. F., & Frenk, C. S. 1998, ApJ, 503, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Elíasdóttir, Á., Limousin, M., Richard, J., et al. 2007, [arXiv:0710.5636] [Google Scholar]
- Evrard, A. E., Bialek, J., Busha, M., et al. 2008, ApJ, 672, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Fedeli, C., & Bartelmann, M. 2007, A&A, 474, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fedeli, C., Meneghetti, M., Bartelmann, M., Dolag, K., & Moscardini, L. 2006, A&A, 447, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fedeli, C., Bartelmann, M., Meneghetti, M., & Moscardini, L. 2007, A&A, 473, 715 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fedeli, C., Bartelmann, M., Meneghetti, M., & Moscardini, L. 2008, A&A, 486, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilbank, D. G., Yee, H. K. C., Ellingson, E., et al. 2007, AJ, 134, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Gioia, I., & Luppino, G. 1994, ApJS, 94, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Gladders, M. D., & Yee, H. K. C. 2001, in The New Era of Wide Field Astronomy, ed. R. Clowes, A. Adamson, & G. Bromage, ASP Conf. Ser., 232, 126 [Google Scholar]
- Gladders, M., Hoekstra, H., Yee, H., Hall, P., & Barrientos, L. 2003, ApJ, 593, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlöber, S., & Yepes, G. 2007, ApJ, 664, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Hennawi, J. F., Dalal, N., Bode, P., & Ostriker, J. P. 2007, ApJ, 654, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Hicks, A. K., Ellingson, E., Hoekstra, H., et al. 2007, ApJ, 671, 1446 [NASA ADS] [CrossRef] [Google Scholar]
- Hicks, A. K., Ellingson, E., Bautz, M., et al. 2008, ApJ, 680, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Hilbert, S., White, S. D. M., Hartlap, J., & Schneider, P. 2008, MNRAS, 386, 1845 [NASA ADS] [CrossRef] [Google Scholar]
- Horesh, A., Maoz, D., Ebeling, H., Seidel, G., & Bartelmann, M. 2010, MNRAS, 781 [Google Scholar]
- Kaiser, N., Squires, G., & Broadhurst, T. 1995, ApJ, 449, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Gottlöber, S., Kravtsov, A. V., & Khokhlov, A. M. 1999, ApJ, 516, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2010, ApJS, submitted [arXiv:1001.4538] [Google Scholar]
- Le Fevre, O., Hammer, F., Angonin, M. C., Gioia, I. M., & Luppino, G. A. 1994, ApJ, 422, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Lenzen, F., Schindler, S., & Scherzer, O. 2004, A&A, 416, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Richard, J., Kneib, J., et al. 2008, A&A, 489, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lo Verde, M., Miller, A., Shandera, S., & Verde, L. 2008, J. Cosmol. Astro-Part. Phys., 4, 14 [Google Scholar]
- Luppino, G., Gioia, I., Hammer, F., Le Fèvre, O., & Annis, J. 1999, A&AS, 136, 117 [Google Scholar]
- Meneghetti, M., Bolzonella, M., Bartelmann, M., Moscardini, L., & Tormen, G. 2000, MNRAS, 314, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Bartelmann, M., & Moscardini, L. 2003a, MNRAS, 346, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Bartelmann, M., & Moscardini, L. 2003b, MNRAS, 340, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Argazzi, R., Pace, F., et al. 2007, A&A, 461, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneghetti, M., Fedeli, C., Pace, F., Gottlöber, S., & Yepes, G. 2010, A&A, 519, A90 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayan, R., & Bartelmann, M. 1999, in Formation of Structure in the Universe, ed. A. Dekel, & J. Ostriker (Cambridge: Cambridge University Press), 360 [Google Scholar]
- Navarro, J., Frenk, C., & White, S. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Hennawi, J. F., Gladders, M. D., et al. 2009, ApJ, 699, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Padmanabhan, T., & Subramanian, K. 1988, MNRAS, 233, 265 [NASA ADS] [Google Scholar]
- Puchwein, E., Bartelmann, M., Dolag, K., & Meneghetti, M. 2005, A&A, 442, 405 [Google Scholar]
- Raymond, J. C., & Smith, B. W. 1977, ApJS, 35, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Smith, G. P., Kneib, J., et al. 2010, MNRAS, 313 [Google Scholar]
- Seidel, G., & Bartelmann, M. 2007, A&A, 472, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shaw, L. D., Weller, J., Ostriker, J. P., & Bode, P. 2006, ApJ, 646, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D., Verde, L., Peiris, H., Komatsu, E., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, K., & Cowling, S. A. 1986, MNRAS, 219, 333 [NASA ADS] [Google Scholar]
- Torri, E., Meneghetti, M., Bartelmann, M., et al. 2004, MNRAS, 349, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Wambsganss, J., Ostriker, J. P., & Bode, P. 2008, ApJ, 676, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, Z. L., Han, J. L., & Liu, F. S. 2010, MNRAS, 407, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Wojtak, R., & Lokas, E. L. 2010, MNRAS, submitted [Google Scholar]
- Yee, H. K. C., & Ellingson, E. 2003, ApJ, 585, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Yepes, G., Sevilla, R., Gottlöber, S., & Silk, J. 2007, ApJ, 666, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., & Gonzalez, A. 2003, ApJ, 584, 691 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{14962f1}
\vspace*{5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg31.png)
|
Figure 1: The redshift distributions of strong lensing clusters in the M AREN OSTRUM U NIVERSE. The black histogram considers all clusters displaying critical lines, the red one those with a non-vanishing cross section for giant arcs, and the blue one those expected to produce at least one giant arc on average. The thick solid green curve represents the lensing efficiency, given by the normalized lensing distance, while the dashed one represents the lensing efficiency weighted for the cluster abundance (see the text for details). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm]{14962f2}
\vspace*{8mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg42.png)
|
Figure 2:
The correlation between the logarithm of the virial mass (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm]{14962f3}
\vspace*{-2.5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg53.png)
|
Figure 3:
The distribution of the logarithm of cross sections for giant arcs (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm]{14962f4}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg66.png)
|
Figure 4:
The correlation between the logarithm of the cross section for giant arcs (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm]{14962f5}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg68.png)
|
Figure 5:
The distribution of the logarithm of cross sections for giant arcs (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{ \includegraphics[width=8cm]{14962f6a} \includegraphics[width=8cm]{14962f6b} }\vspace*{2.5mm}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg86.png)
|
Figure 6: Left panel. The differential optical depth for giant arcs obtained by all clusters in the M AREN OSTRUM U NIVERSE as a function of lens redshift (black solid line). The red dashed line represents the synthetic differential optical depth obtained with the procedure outlined in the text (q=3.5), while the shaded area represents the effect of a 30% uncertainty on the minimum mass at the pivotal redshift (see the text for details). Right panel. Same as the left panel but with the blue and green dashed lines now representing the synthetic optical depths computed with values of q different from 3.5, as labeled. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{14962f7}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg99.png)
|
Figure 7: The redshift evolution of the two parameters defining the best fit x-y relation (see the text for details), with the respective standard errors. The black and red solid horizontal lines represent the respective redshift averages, while the green horizontal line represents the slope expected for a SIS lens model. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm]{14962f8}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg106.png)
|
Figure 8: The difference between the true distribution around the best fit mass-cross section relation and the best Gaussian (blue shaded histograms with black contours) and non-Gaussian (magenta shaded histograms) fits. Results for several different redshift snapshots are shown, as labeled in the plot. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{14962f9}\hfill\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg115.png)
|
Figure 9:
The differential optical depth in the M AREN OSTRUM U NIVERSE computed for all clusters in the simulation (black solid line) and by including only those clusters whose |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{14962f10}
\end{figure}](/articles/aa/full_html/2010/11/aa14962-10/Timg131.png)
|
Figure 10:
The fraction of the total optical depth that is contributed by clusters of the M AREN OSTRUM U NIVERSE with logarithm of the bolometric X-ray luminosity (in units of 1044 erg s-1,
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



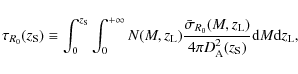
![\begin{displaymath}
\tau_{R_0}(z_{\rm S}) = \int_0^{z_{\rm S}} \left[\sum_{i=1}^...
...i}^{M_{i+1}} N(M,z_{\rm L}) {\rm d}M \right] {\rm d}z_{\rm L},
\end{displaymath}](/articles/aa/full_html/2010/11/aa14962-10/img26.png)
![\begin{displaymath}
\sigma_{R_0} = \frac{32\pi^3 D_{\rm A}^2(z_{\rm L},z_{\rm S}...
...t[\frac{h(z_{\rm L})M}{10^{15}~M_\odot} \right]^{4\alpha}\cdot
\end{displaymath}](/articles/aa/full_html/2010/11/aa14962-10/img57.png)
![\begin{displaymath}
p(y-y_x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left[-\frac{(y-y_...
...gma^2}\right] \left[ 1+\sigma H_3(y-y_0)\frac{S_3}{6} \right],
\end{displaymath}](/articles/aa/full_html/2010/11/aa14962-10/img69.png)
![\begin{displaymath}
M_{\rm min}(z_{\rm L}) = M_{\rm min, p} \left[\frac{\varepsilon(z_{\rm L,p})}{\varepsilon(z_{\rm L})}\right]^q\cdot
\end{displaymath}](/articles/aa/full_html/2010/11/aa14962-10/img98.png)