| Issue |
A&A
Volume 518, July-August 2010
Herschel: the first science highlights
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014227 | |
| Published online | 20 August 2010 | |
 Y/
Y/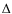 Z
from the analysis of local K dwarfs
Z
from the analysis of local K dwarfs
M. Gennaro1,![]() - P. G. Prada
Moroni2,3 - S. Degl'Innocenti2,3
- P. G. Prada
Moroni2,3 - S. Degl'Innocenti2,3
1 - Max Planck Institute for Astronomy, Königstuhl 17, 69117
Heidelberg, Germany
2 - Physics Department ``E. Fermi'', University of Pisa, Largo B.
Pontecorvo 3, 56127 Pisa, Italy
3 - INFN, Largo B. Pontecorvo 3, 56127 Pisa, Italy
Received 9 February 2010 / Accepted 28 April 2010
Abstract
Context. The stellar helium-to-metal enrichment
ratio, ![]() ,
is a widely studied astrophysical quantity. However, its value has
still not been precisely constrained.
,
is a widely studied astrophysical quantity. However, its value has
still not been precisely constrained.
Aims. This paper is focused on studying the main
sources of uncertainty that affect the
![]() ratio derived from the analysis of the low-main sequence (MS) stars in
the solar neighborhood.
ratio derived from the analysis of the low-main sequence (MS) stars in
the solar neighborhood.
Methods. The possibility of inferring the value of
the helium-to-metal enrichment ratio from the study of low-MS stars
relies on the dependence of the stellar luminosity and effective
temperature on the initial helium and metal abundances. The
![]() ratio is obtained by comparing the magnitude difference between the
observed stars and a reference, theoretical zero age main sequence
(ZAMS) with the related theoretical magnitude differences computed from
a new set of stellar models with up-to-date input physics and a fine
grid of chemical compositions. A Monte Carlo approach has been used to
evaluate the impact of different sources of uncertainty, i.e.
observational errors, evolutionary effects, systematic uncertainties of
the models. As a check of the procedure, the method was applied to a
different data set, namely the low-MS of the Hyades.
ratio is obtained by comparing the magnitude difference between the
observed stars and a reference, theoretical zero age main sequence
(ZAMS) with the related theoretical magnitude differences computed from
a new set of stellar models with up-to-date input physics and a fine
grid of chemical compositions. A Monte Carlo approach has been used to
evaluate the impact of different sources of uncertainty, i.e.
observational errors, evolutionary effects, systematic uncertainties of
the models. As a check of the procedure, the method was applied to a
different data set, namely the low-MS of the Hyades.
Results. Once a set of ZAMS and atmosphere models
had been chosen, we found that the inferred value of
![]() is sensitive to the age of the stellar sample, even if we restricted
the data set to low-luminosity stars. The lack of an accurate age
estimate of low-mass field stars leads to underestimating the inferred
is sensitive to the age of the stellar sample, even if we restricted
the data set to low-luminosity stars. The lack of an accurate age
estimate of low-mass field stars leads to underestimating the inferred
![]() of
of ![]() 2 units.
On the contrary, the method firmly recovers the
2 units.
On the contrary, the method firmly recovers the
![]() value for unevolved samples of stars like the Hyades low-MS. Adopting a
solar-calibrated mixing-length parameter and the PHOENIX GAIA v2.6.1
atmospheric models, we find
value for unevolved samples of stars like the Hyades low-MS. Adopting a
solar-calibrated mixing-length parameter and the PHOENIX GAIA v2.6.1
atmospheric models, we find
![]() once the age correction has been applied. The Hyades sample provided a
perfectly consistent value.
once the age correction has been applied. The Hyades sample provided a
perfectly consistent value.
Conclusions. We have demonstrated that assuming that
low-mass stars in the solar neighborhood can be considered as unevolved
does not necessarily hold, and it may indeed lead to a bias in the
inferred ![]() .
The effect of the still poorly constrained efficiency of the
superadiabatic convection and of different atmosphere models adopted to
transform luminosities and effective temperature into colors and
magnitudes are also discussed.
.
The effect of the still poorly constrained efficiency of the
superadiabatic convection and of different atmosphere models adopted to
transform luminosities and effective temperature into colors and
magnitudes are also discussed.
Key words: Galaxy: fundamental parameters - solar neighborhood - stars: abundances - stars: low-mass
1 Introduction
It is a well known and firm result of stellar evolution studies that the main structural, observational, and evolutionary characteristics of a star of given mass are sensitive to the original chemical composition, i.e., the initial helium and metal abundances, Y and Z, respectively. As a consequence, these parameters also affect the observable quantities of stellar systems from star clusters to galaxies.
While the present Z in a stellar atmosphere can be obtained by direct spectroscopic measurements of some tracer element, mainly iron, with the additional assumption on the mixture of heavy elements, the situation of Y is completely different. In the vast majority of stars, the helium lines cannot be observed, with the exception of those hotter than 20 000 K. This means that, for the low-mass stars, which are the most common and long-lasting objects in the Universe, helium can be directly observed only in advanced evolutionary phases, as the blue part of the horizontal branch or in the post-asymptotic giant branch. Thus, the actually measured helium abundance is not the original one, but instead the result of several complex processes, like dredge-up of nuclearly processed material, diffusion, and radiative levitation, which severely alter the surface chemical composition. As a consequence, to evaluate the original Y, the only possibility is to rely on indirect methods. This explains why such an important parameter is still poorly constrained.
As suggested by Peimbert
& Torres-Peimbert in 1974
from analysis of the chemical composition of the HII regions in the
Large Magellanic Cloud, a common approach in both stellar and
population synthesis models is to assume a linear relationship between
the original Y and Z,
where
In the past four decades there has been continuous effort to
constrain both the ![]() (see e.g. Kunth
& Sargent 1983; Pagel et al. 1986; Peebles 1966;
Peimbert
& Torres-Peimbert 1974; Lequeux et al. 1979; Peimbert
& Torres-Peimbert 1976; Churchwell et al. 1974;
Kunth 1986;
Izotov
et al. 1994; Peimbert et al. 2002; Olive &
Steigman 1995; Peimbert et al. 2007; Izotov
et al. 1997; Dunkley et al. 2009; Izotov
et al. 2007; Olive et al. 1997; Pagel
et al. 1992; Spergel et al. 2007; Mathews
et al. 1993) and the ratio
(see e.g. Kunth
& Sargent 1983; Pagel et al. 1986; Peebles 1966;
Peimbert
& Torres-Peimbert 1974; Lequeux et al. 1979; Peimbert
& Torres-Peimbert 1976; Churchwell et al. 1974;
Kunth 1986;
Izotov
et al. 1994; Peimbert et al. 2002; Olive &
Steigman 1995; Peimbert et al. 2007; Izotov
et al. 1997; Dunkley et al. 2009; Izotov
et al. 2007; Olive et al. 1997; Pagel
et al. 1992; Spergel et al. 2007; Mathews
et al. 1993) and the ratio
![]() (Perrin
et al. 1977; Fernandes et al. 1996;
Casagrande
et al. 2007; Renzini 1994; Peimbert
& Serrano 1980; Faulkner 1967; Pagel &
Portinari 1998; Lequeux et al. 1979; Fukugita
& Kawasaki 2006; Izotov & Thuan 2004; Pagel
et al. 1992; Jimenez et al. 2003; Peimbert 1986).
(Perrin
et al. 1977; Fernandes et al. 1996;
Casagrande
et al. 2007; Renzini 1994; Peimbert
& Serrano 1980; Faulkner 1967; Pagel &
Portinari 1998; Lequeux et al. 1979; Fukugita
& Kawasaki 2006; Izotov & Thuan 2004; Pagel
et al. 1992; Jimenez et al. 2003; Peimbert 1986).
Indeed, as previously mentioned, the relationship between Y
and Z adopted in stellar models directly affects
some important quantities of stellar systems, both resolved and not,
inferred by comparing observations and theoretical predictions. Thus, a
precise determination of ![]() and
and ![]() is paramount for studies not only of stellar evolution, but also of
galaxy evolution. Furthermore, an accurate estimate of
is paramount for studies not only of stellar evolution, but also of
galaxy evolution. Furthermore, an accurate estimate of ![]() is of great cosmological interest, because it constrains the early
evolution of the
Universe, when the Big Bang nucleosynthesis occurred. In this paper we
focus on the value of the
is of great cosmological interest, because it constrains the early
evolution of the
Universe, when the Big Bang nucleosynthesis occurred. In this paper we
focus on the value of the
![]() ratio. In the past, several techniques have been used to determine such
a ratio by means of HII regions, both galactic and extragalactic,
planetary nebulae (PNe), the Sun and chemical evolution models of the
Galaxy (see Sect. 9
for a brief summary of these results).
ratio. In the past, several techniques have been used to determine such
a ratio by means of HII regions, both galactic and extragalactic,
planetary nebulae (PNe), the Sun and chemical evolution models of the
Galaxy (see Sect. 9
for a brief summary of these results).
An alternative and well established way to determine the value
of the helium-to-metallicity enrichment ratio takes advantage of the
dependence of the location of stars in the Hertzsprung-Russell (HR)
diagram on their helium content. From the study of stellar populations
in the galactic bulge Renzini (1994)
inferred
![]() .
A frequently adopted approach relies on the analysis of the fine
structure of the low-MS of the local field stars in the HR diagram.
Pioneers of such an approach have been Faulkner, who found
.
A frequently adopted approach relies on the analysis of the fine
structure of the low-MS of the local field stars in the HR diagram.
Pioneers of such an approach have been Faulkner, who found
![]() (Faulkner 1967) and
Perrin and collaborators, who obtained
(Faulkner 1967) and
Perrin and collaborators, who obtained
![]() (Perrin et al. 1977).
Following these early studies, Fernandes
et al. (1996)
constrained the value of
(Perrin et al. 1977).
Following these early studies, Fernandes
et al. (1996)
constrained the value of
![]() to be higher than 2, by comparing the broadening in the HR diagram of
the low-mass MS stars in the solar neighborhood and the theoretical
ZAMS of several Y and Z. With a
similar approach but taking advantage of Hipparcos data, Pagel & Portinari (1998)
inferred
to be higher than 2, by comparing the broadening in the HR diagram of
the low-mass MS stars in the solar neighborhood and the theoretical
ZAMS of several Y and Z. With a
similar approach but taking advantage of Hipparcos data, Pagel & Portinari (1998)
inferred ![]() .
This kind of approach culminated recently in the works by Jimenez et al. (2003)
and Casagrande et al.
(2007) who provided, respectively,
.
This kind of approach culminated recently in the works by Jimenez et al. (2003)
and Casagrande et al.
(2007) who provided, respectively,
![]() and
and ![]() .
.
The present analysis deals with the determination of the
![]() ratio by means of the comparison between the local K dwarf
stars, for which accurate measures of both the [Fe/H] and parallaxes
are available, and state-of-the-art stellar models. A great effort has
been devoted to discuss the effect of the main uncertainties still
present in stellar models on the inferred value of
ratio by means of the comparison between the local K dwarf
stars, for which accurate measures of both the [Fe/H] and parallaxes
are available, and state-of-the-art stellar models. A great effort has
been devoted to discuss the effect of the main uncertainties still
present in stellar models on the inferred value of
![]() .
.
In Sect. 2 we present the set of low-mass stellar models we have computed for this paper; in Sect. 3 we describe the data set we have used; Sect. 4 contains the description of the analysis method, while Sect. 5 deals with the possible sources of uncertainty that could affect the method itself. Results for the adopted data set are presented in Sect. 6. In Sect. 7 we investigate the possibility of a non linear relation between Y and Z. In Sect. 8 we apply our method to an independent and unevolved set of stars, i.e. the Hyades low-main sequence. We compare our results to those obtained by other authors, with independent methods, in Sect. 9. Section 10 contains the final discussion and summary of the whole paper.
2 The models
The stellar models have been computed on purpose for the present work
with an updated version of the FRANEC evolutionary code which includes
the state-of the art input physics (see e.g. Chieffi & Straniero 1989; Tognelli
et al. 2010; Valle et al. 2009; Degl'Innocenti
et al. 2008).
The main updating of the code with respect to previous versions include
the 2006 release of the OPAL Equation of state (EOS) ![]() (see also Rogers et al. 1996) and,
for temperatures higher than
12 000 K, radiative opacity tables
(see also Rogers et al. 1996) and,
for temperatures higher than
12 000 K, radiative opacity tables![]() (see also Iglesias & Rogers 1996),
while the opacities by Ferguson
et al. (2005) are adopted for lower temperatures
(see also Iglesias & Rogers 1996),
while the opacities by Ferguson
et al. (2005) are adopted for lower temperatures![]() .
The electron-conduction opacities are by Shternin
& Yakovlev (2006) (see also Potekhin
1999). The opacity tables have been calculated by assuming
the solar mixture by Asplund
et al. (2005).
.
The electron-conduction opacities are by Shternin
& Yakovlev (2006) (see also Potekhin
1999). The opacity tables have been calculated by assuming
the solar mixture by Asplund
et al. (2005).
The extension of the convectively unstable regions is
determined by using the classical Schwarzschild criterion. The mixing
length formalism (Böhm-Vitense 1958)
is used to model the super-adiabatic convection typical of the outer
layers. As it is well known, within this simplified scheme, the
efficiency of convective transport depends on a free parameter that has
to be calibrated using observations. We adopted the usual ``solar''
calibration of the ![]() of the mixing-length. More in detail, this means that we chose the
value of
of the mixing-length. More in detail, this means that we chose the
value of ![]() provided by a standard solar model (SSM) computed with the same FRANEC
code and the same input physics we used to compute all the other
stellar tracks.
provided by a standard solar model (SSM) computed with the same FRANEC
code and the same input physics we used to compute all the other
stellar tracks.
Note that the ``solar'' calibrated value of the ![]() parameter strongly depends on the chosen outer boundary conditions
needed to solve the differential equations describing the inner stellar
structure, that is, the main physical quantities at the base of the
photosphere (e.g. Tognelli
et al. 2010; Montalban et al. 2004).
In order to get these quantities, we followed the procedure commonly
adopted in stellar computations, which consists in a direct integration
of the equations describing a 1D atmosphere in hydrostatic equilibrium
and in the diffusive approximation of radiative
transport, plus a gray T(
parameter strongly depends on the chosen outer boundary conditions
needed to solve the differential equations describing the inner stellar
structure, that is, the main physical quantities at the base of the
photosphere (e.g. Tognelli
et al. 2010; Montalban et al. 2004).
In order to get these quantities, we followed the procedure commonly
adopted in stellar computations, which consists in a direct integration
of the equations describing a 1D atmosphere in hydrostatic equilibrium
and in the diffusive approximation of radiative
transport, plus a gray T(![]() )
relationship between the temperature and the optical depth. The
classical semiempirical T(
)
relationship between the temperature and the optical depth. The
classical semiempirical T(![]() )
relationship by Krishna Swamy (1966)
has been chosen. If a non-gray and more realistic model atmosphere is
used, the solar calibrated value of
)
relationship by Krishna Swamy (1966)
has been chosen. If a non-gray and more realistic model atmosphere is
used, the solar calibrated value of ![]() is
different (see e.g. Tognelli
et al. 2010, for a detailed discussion).
is
different (see e.g. Tognelli
et al. 2010, for a detailed discussion).
Moreover, the ``solar'' calibrated value of the ![]() parameter depends also on the input physics adopted in the SSM
computation. Thus, to the sake of consistency, if the solar calibration
approach is followed to fix the
parameter depends also on the input physics adopted in the SSM
computation. Thus, to the sake of consistency, if the solar calibration
approach is followed to fix the ![]() parameter of a set of stellar models, the input physics and boundary
conditions adopted to compute these models have to be the same as those
used in the reference SSM. In spite of its widespread use, the solar
calibration of the mixing-length does not rely on a firm theoretical
ground, since there are not compelling reasons to guarantee that the
efficiency of superadiabatic convective transport should be same in
stars of different mass and/or in different stages of evolution (see
e.g. Montalban et al. 2004,
and references therein). However, for what concerns the present paper,
such an
approach should be quite safe, since we deal with stars in the mass
range 0.7-0.9
parameter of a set of stellar models, the input physics and boundary
conditions adopted to compute these models have to be the same as those
used in the reference SSM. In spite of its widespread use, the solar
calibration of the mixing-length does not rely on a firm theoretical
ground, since there are not compelling reasons to guarantee that the
efficiency of superadiabatic convective transport should be same in
stars of different mass and/or in different stages of evolution (see
e.g. Montalban et al. 2004,
and references therein). However, for what concerns the present paper,
such an
approach should be quite safe, since we deal with stars in the mass
range 0.7-0.9
![]() and that are on the Main
Sequence. We also computed models with a
different value of
and that are on the Main
Sequence. We also computed models with a
different value of ![]() ,
namely 2.4, in order to quantify the effect of an uncertainty in the
efficiency of the mixing-length on the inferred
,
namely 2.4, in order to quantify the effect of an uncertainty in the
efficiency of the mixing-length on the inferred
![]() ratio.
ratio.
Our reference theoretical models have been transformed from
the
![]() to the
to the ![]() diagram by means of synthetic photometry using the spectra database
GAIA v2.6.1 calculated from PHOENIX model atmospheres (Brott et al. 2005). We
performed additional simulations adopting the Castelli
& Kurucz (2003) model atmospheres, to check the
effect of the adopted color transformations on the inferred
diagram by means of synthetic photometry using the spectra database
GAIA v2.6.1 calculated from PHOENIX model atmospheres (Brott et al. 2005). We
performed additional simulations adopting the Castelli
& Kurucz (2003) model atmospheres, to check the
effect of the adopted color transformations on the inferred
![]() ratio.
ratio.
The original helium abundance in the stellar models has been
obtained following Eq. (1),
where Z, once a solar mixture is assumed, is
directly related to the observable [Fe/H] by
We used for
Stellar models have been calculated for 9
![]() values (0.5, 1, 2 ... 8) and 5 [Fe/H] values (from -0.6 to +0.2 in
steps of 0.2 dex). For each of these 45 combinations we
calculated evolutionary tracks for 11 stellar masses (from 0.5
to 1.0
values (0.5, 1, 2 ... 8) and 5 [Fe/H] values (from -0.6 to +0.2 in
steps of 0.2 dex). For each of these 45 combinations we
calculated evolutionary tracks for 11 stellar masses (from 0.5
to 1.0
![]() in steps of 0.05
in steps of 0.05
![]() )
in order to build zero age main sequence (ZAMS) curves that cover the
whole HR region corresponding to the adopted data set (see
Sect. 3). For each stellar mass we calculated its evolution
starting from the pre-main sequence (PMS) phase.
)
in order to build zero age main sequence (ZAMS) curves that cover the
whole HR region corresponding to the adopted data set (see
Sect. 3). For each stellar mass we calculated its evolution
starting from the pre-main sequence (PMS) phase.
To determine the ZAMS position we used the following operative
criterion: we calculated the local Kelvin-Helmoltz timescale for each
model, i.e.
![]() ,
where
,
where ![]() and L are the gravitational binding energy and the
total luminosity; then we compared this number with the local
evolutionary timescale,
and L are the gravitational binding energy and the
total luminosity; then we compared this number with the local
evolutionary timescale,
![]() ,
i.e. the inverse of the instantaneous rate of change of the luminosity.
We found that a good operative definition of ZAMS is obtained by taking
the first model for which
,
i.e. the inverse of the instantaneous rate of change of the luminosity.
We found that a good operative definition of ZAMS is obtained by taking
the first model for which
![]() .
.
As previously mentioned, an additional set of models, with the
related ZAMS, has been computed for a value of the mixing-length
parameter, ![]() .
Thus, the present analysis can rely on a very fine grid of stellar
models consisting of about a thousand evolutionary tracks calculated
from the PMS phase to the central hydrogen exhaustion.
.
Thus, the present analysis can rely on a very fine grid of stellar
models consisting of about a thousand evolutionary tracks calculated
from the PMS phase to the central hydrogen exhaustion.
3 The data set
The stars of our sample have been selected among the HIPPARCOS (ESA 1997) stars with relative error on
the parallax less than 5%. B and V
band photometry are also taken from HIPPARCOS data set and they have
typical errors between 0.01 and 0.02 mag; combining them gives
(B -V) colors with errors on the
order of 0.03 mag. From the parallax and the observed V magnitude
we computed the absolute magnitude MV;
with the quoted typical errors on V and parallax,
the error on the absolute magnitude is ![]() 0.1 mag, largely dominated by the error
on the parallax.
Given the low values of the distances, always less than 30 pc
for the stars in our sample, we also assume that the reddening is
negligible, so that (B
- V)0 =(B
- V).
Our sample has been restricted only to those stars with
0.1 mag, largely dominated by the error
on the parallax.
Given the low values of the distances, always less than 30 pc
for the stars in our sample, we also assume that the reddening is
negligible, so that (B
- V)0 =(B
- V).
Our sample has been restricted only to those stars with ![]() in order to take objects with long evolutionary time scales and hence
minimize evolutionary effects.
in order to take objects with long evolutionary time scales and hence
minimize evolutionary effects.
Table 1: [Fe/H] for the 4 stars in common in the Taylor (2005) and Geneva-Copenhagen catalogs.
[Fe/H] determinations are taken from the Geneva-Copenhagen
survey of the Solar neighborhood catalog (Nordström
et al. 2004, hereafter N04), for
86 objects, and from the catalog by Taylor (Taylor 2005, hereafter T05) for
21 objects. Of these 107 objects, 4 have [Fe/H]
determinations from both catalogs; in these cases we only count the
stars once, using their T05 metallicities. The total number is then
reduced to 103 stars.
N04 metallicity values are derived by a calibrated relation between
Strömgren photometry measurements and spectroscopic determinations of
metal abundances for a subset of objects.
The T05 catalog is instead a collection of spectroscopic
determinations of metal abundances from the literature, where different
results are put by the author on the same temperature scale; if more
determinations are available for the same object, they are
weight-averaged according to their quality. As pointed out in Taylor (2005), determination of
[Fe/H] from different authors may suffer strong systematic deviations,
due to the different temperature scale chosen. The author showed that
it is possible to reach a very good zero-point accuracy when data from
different sources are put together in an appropriate way.
Indeed a systematic difference in metallicity can be seen for the 4
stars that we have in common in our subsamples of the N04 and T05
catalogs. The metallicities for these objects are shown in
Table 1.
There we also show the new determinations of Geneva-Copenhagen
metallicities using an improved calibration (Holmberg
et al. 2007, hereafter H07). As shown by the
authors, the N04 and H07 spectro-photometric calibrations give
internally consistent results; only one of the 4 stars in common shows
a small change in the [Fe/H] between the two catalogs. The average
shift in [Fe/H] on this small sample and its standard deviation is
![]() .
Taylor (2005) calculates the
expected offset between his metallicity scale and the Nordström et al. (2004)
one; according to his Table 10, for all the stars in our N04
sub-sample this offset is expected to be
.
Taylor (2005) calculates the
expected offset between his metallicity scale and the Nordström et al. (2004)
one; according to his Table 10, for all the stars in our N04
sub-sample this offset is expected to be
![]() ,
somewhat lower than what we find for our stars in common, which, anyway
are only 4. We decided to apply the -0.023 offset to the
Geneva-Copenhagen metallicities in their old version, i.e. the N04,
since it is for the Nordström
et al. (2004) calibration that Taylor (2005) evaluates the
zero-point offset.
,
somewhat lower than what we find for our stars in common, which, anyway
are only 4. We decided to apply the -0.023 offset to the
Geneva-Copenhagen metallicities in their old version, i.e. the N04,
since it is for the Nordström
et al. (2004) calibration that Taylor (2005) evaluates the
zero-point offset.
In the Geneva-Copenhagen survey the repeated radial velocity measurements allow detections of almost all the possible binaries in the sample; we flagged out all the suspect binaries in the catalog. The Taylor (2005) [Fe/H] catalog is instead free of such contaminants, given its spectroscopic nature.
Our final sample is made of 103 stars with good parallaxes,
photometry and [Fe/H] determinations. The typical errors are given by:
![]() ,
,
![]() and
and
![]() .
The error on the absolute magnitude is mainly due to the error on the
parallax.
Metallicities range from [Fe/H] = -0.6 dex
to +0.2 dex; magnitudes range from MV
= 6.0 mag to
.
The error on the absolute magnitude is mainly due to the error on the
parallax.
Metallicities range from [Fe/H] = -0.6 dex
to +0.2 dex; magnitudes range from MV
= 6.0 mag to ![]() mag.
The color-magnitude diagram (CMD) for the data is shown in
Fig. 1,
where the data are grouped in [Fe/H] bins 0.2 dex wide.
mag.
The color-magnitude diagram (CMD) for the data is shown in
Fig. 1,
where the data are grouped in [Fe/H] bins 0.2 dex wide.

|
Figure 1:
The data color-magnitude diagram. Overplotted are three ZAMS all
computed with |
| Open with DEXTER | |
4 The method
The idea to determine the
![]() ratio using the position of low-mass MS stars in the HR diagram relies
on the well known dependence of their luminosity and effective
temperature on the original Y and Z.
It is in fact firmly established that an increase of Y
at fixed Z makes a star brighter and hotter. A
decrease of Z at fixed Y leads
to the same result. Such a behavior is the consequence of the effect on
the opacity and mean molecular weight, i.e. the former gets higher as Z
increases, while the latter grows with Y.
ratio using the position of low-mass MS stars in the HR diagram relies
on the well known dependence of their luminosity and effective
temperature on the original Y and Z.
It is in fact firmly established that an increase of Y
at fixed Z makes a star brighter and hotter. A
decrease of Z at fixed Y leads
to the same result. Such a behavior is the consequence of the effect on
the opacity and mean molecular weight, i.e. the former gets higher as Z
increases, while the latter grows with Y.
As early shown by Faulkner
(1967), who studied the effect of chemical composition
variations on the position of theoretical ZAMS, a simple but
instructive explanation of this behavior can be obtained by means of
homology relations (see also Fernandes
et al. 1996). Within this framework, it can be shown
that varying Y and Z in such a
way that ![]() ,
leaves the bolometric magnitude
,
leaves the bolometric magnitude
![]() of ZAMS at fixed effective temperature unchanged. This explains why the
broadening of the local low-MS provides a
of ZAMS at fixed effective temperature unchanged. This explains why the
broadening of the local low-MS provides a
![]() indicator.
indicator.
However, this is not the whole story, as clearly proven by Castellani et al. (1999),
who computed a fine grid of full evolutionary models of ZAMS stars with
several metal and helium abundances.
They showed that the ![]() of ZAMS at a given
of ZAMS at a given ![]() depends quadratically on
depends quadratically on ![]() and that only in a narrow range around the solar metallicity such a
dependence can be reasonably linearized to
and that only in a narrow range around the solar metallicity such a
dependence can be reasonably linearized to
![]() (see also Fernandes
et al. 1996). In addition, when comparing ZAMS
models with real stars, one has to take into account the effect on the
color indices. Castellani
et al. (1999) showed that a
(see also Fernandes
et al. 1996). In addition, when comparing ZAMS
models with real stars, one has to take into account the effect on the
color indices. Castellani
et al. (1999) showed that a
![]() is required to keep unchanged the B-V
color at MV
= 6 in a narrow range around
is required to keep unchanged the B-V
color at MV
= 6 in a narrow range around
![]() .
The discrepancy between the
.
The discrepancy between the
![]() required to keep the
required to keep the ![]() and B-V unchanged clearly proves
the crucial role played by the model atmospheres. In Sect. 5.4 we will
further discuss the effect of different assumptions on the
color-transformations on the inferred
and B-V unchanged clearly proves
the crucial role played by the model atmospheres. In Sect. 5.4 we will
further discuss the effect of different assumptions on the
color-transformations on the inferred
![]() .
.
The use of ZAMS models is allowed as long as observational
data really lie on the ZAMS, or very close to it.
Although this assumption is implicit in many studies which derive the
![]() from the fine structure of the low-MS, a detailed discussion of the
effect of a deviation from such an assumption on the inferred value of
the helium-to-metal enrichment ratio is still lacking.
The reason is that very faint (
from the fine structure of the low-MS, a detailed discussion of the
effect of a deviation from such an assumption on the inferred value of
the helium-to-metal enrichment ratio is still lacking.
The reason is that very faint (![]() )
local MS stars are usually considered as if they
were still on the ZAMS, since their evolutionary timescales are longer
than the Galactic Disk age. We will show in Sect. 5.2 that
this assumption is indeed critical, since underestimating the effects
of age on both the position of the stars in the CMD and the diffusion
of heavy elements below the photosphere leads to a severe bias in the
final estimate of the enrichment ratio. We take this bias into account
when giving the final result on
)
local MS stars are usually considered as if they
were still on the ZAMS, since their evolutionary timescales are longer
than the Galactic Disk age. We will show in Sect. 5.2 that
this assumption is indeed critical, since underestimating the effects
of age on both the position of the stars in the CMD and the diffusion
of heavy elements below the photosphere leads to a severe bias in the
final estimate of the enrichment ratio. We take this bias into account
when giving the final result on
![]() for our work.
for our work.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14227f02.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14227-10/Timg52.png)
|
Figure 2:
Illustrative example of how theoretichal and observational
differences are computed and used to produce a
|
| Open with DEXTER | |
Following Jimenez et al.
(2003), we did not directly use the broadening of the local
low-MS in the CMD, instead, we compared models and data in a diagram
like that of Fig. 2,
right panel. After choosing a reference ZAMS, theoretical
differences in magnitude, ![]() ,
between that reference ZAMS and the other ZAMS curves, computed for
different values of [Fe/H] and
,
between that reference ZAMS and the other ZAMS curves, computed for
different values of [Fe/H] and
![]() ,
are measured at a fixed value of the color index B
- V (see Fig. 2, left
panel).
We checked that, within the current accuracy of the data, the derived
,
are measured at a fixed value of the color index B
- V (see Fig. 2, left
panel).
We checked that, within the current accuracy of the data, the derived
![]() value it is not affected by changing the reference ZAMS and/or the
color index value. In fact, the ZAMS loci, in the range of magnitudes
and colors that is involved here, are almost parallel to each other and
the effect of the uncertain position of the star caused by the
observational errors is much stronger than that caused by a different
choice of the reference ZAMS and/or the color index value.
value it is not affected by changing the reference ZAMS and/or the
color index value. In fact, the ZAMS loci, in the range of magnitudes
and colors that is involved here, are almost parallel to each other and
the effect of the uncertain position of the star caused by the
observational errors is much stronger than that caused by a different
choice of the reference ZAMS and/or the color index value.
The differences ![]() obviously depend on the chemical composition, i.e. on both
obviously depend on the chemical composition, i.e. on both
![]() and [Fe/H], as is clearly visible in Fig. 2 (right
panel). Observational differences between the
data set and the same reference ZAMS are also measured in the way
illustrated in Fig. 2
(left panel) and are plotted in Fig. 2 (right
panel) as a function of [Fe/H].
and [Fe/H], as is clearly visible in Fig. 2 (right
panel). Observational differences between the
data set and the same reference ZAMS are also measured in the way
illustrated in Fig. 2
(left panel) and are plotted in Fig. 2 (right
panel) as a function of [Fe/H].
To find the value of
![]() that gives the best fit to the data, we assign to each star errors in
the three quantities MV,
B - V and [Fe/H]. The errors in MV
and B - V are assigned in the
CMD, i.e. before the differences
that gives the best fit to the data, we assign to each star errors in
the three quantities MV,
B - V and [Fe/H]. The errors in MV
and B - V are assigned in the
CMD, i.e. before the differences
![]() are calculated; then the error in [Fe/H] is assigned in the
are calculated; then the error in [Fe/H] is assigned in the
![]() diagram.
Magnitude and color errors are considered to be distributed as Gaussian
with
diagram.
Magnitude and color errors are considered to be distributed as Gaussian
with ![]() equal to the quoted uncertainty for that star; the assumption of
Gaussian errors is reasonable, considering that they come from the
HIPPARCOS photometric errors plus (for the absolute magnitude) the
HIPPARCOS parallax error; these two sources of error are independent
and our objects are all close by and have well determined parallaxes,
so that they don't suffer the Lutz-Kelker bias. Regarding the [Fe/H]
value the situation is different, since the errors associated to each
value are highly affected by systematic effects like the choice of the
temperature scale; for this reason, and since we cannot reconstruct the
real error distribution in [Fe/H], we adopted an uniform distribution
of [Fe/H] errors. Anyway, we have also checked that a Gaussian
distribution for [Fe/H] values leaves the results essentially
unaffected.
equal to the quoted uncertainty for that star; the assumption of
Gaussian errors is reasonable, considering that they come from the
HIPPARCOS photometric errors plus (for the absolute magnitude) the
HIPPARCOS parallax error; these two sources of error are independent
and our objects are all close by and have well determined parallaxes,
so that they don't suffer the Lutz-Kelker bias. Regarding the [Fe/H]
value the situation is different, since the errors associated to each
value are highly affected by systematic effects like the choice of the
temperature scale; for this reason, and since we cannot reconstruct the
real error distribution in [Fe/H], we adopted an uniform distribution
of [Fe/H] errors. Anyway, we have also checked that a Gaussian
distribution for [Fe/H] values leaves the results essentially
unaffected.
Once a ``new'' data set is created from the original value
plus the errors, we determine the theoretical curve which minimizes the
quantity:
where j runs over the curves (i.e. over different

|
Figure 3:
Results of 105 simulation runs to determine the
best fitting |
| Open with DEXTER | |
5 Analysis of possible sources of uncertainty using artificial data sets
To check the reliability of the procedure described above and to
evaluate the contribution of the various possible sources of
uncertainty, we applied our method to a number of artificial data sets
with controlled input parameters.
These sets have been created by interpolation in our fine grid of
stellar models.
Stellar masses are randomly generated from a power law initial mass
function (IMF)
![]() with a slope of
with a slope of ![]() (Kroupa 2001;
Salpeter
1955); an IMF with a unique value of the exponent is a good
law in our range of simulated masses (
(Kroupa 2001;
Salpeter
1955); an IMF with a unique value of the exponent is a good
law in our range of simulated masses (
![]() ).
The chemical composition is calculated by fixing the input value of
).
The chemical composition is calculated by fixing the input value of
![]() and extracting random values for [Fe/H] for each star; Y
and Z are then calculated using the two
Eqs. (1)
and (2).
In what concerns the stellar ages generation, we performed different
kind of simulations, adopting three age-laws (i.e. star formation
rates, SFRs), namely a Dirac's delta centered about a given age (i.e.
coeval stars), a uniform and an exponentially decaying age
distribution, respectively, in the range 0-7 Gyr, a reasonable
approximation for the age of the galactic disk.
and extracting random values for [Fe/H] for each star; Y
and Z are then calculated using the two
Eqs. (1)
and (2).
In what concerns the stellar ages generation, we performed different
kind of simulations, adopting three age-laws (i.e. star formation
rates, SFRs), namely a Dirac's delta centered about a given age (i.e.
coeval stars), a uniform and an exponentially decaying age
distribution, respectively, in the range 0-7 Gyr, a reasonable
approximation for the age of the galactic disk.
Since the FRANEC code includes a treatment of diffusion of the
elements, given a star of age ![]() ,
we take from the models the corresponding surface value of [Fe/H]
,
we take from the models the corresponding surface value of [Fe/H]![]() ,
which is different from the initial value [Fe/H]0
because of diffusion itself. This is the value that we use for the
recovery, because in a real star the observed [Fe/H] is the present
one and not the initial. Note that neglecting diffusion may lead to a
bias (an underestimate, indeed) in the final
,
which is different from the initial value [Fe/H]0
because of diffusion itself. This is the value that we use for the
recovery, because in a real star the observed [Fe/H] is the present
one and not the initial. Note that neglecting diffusion may lead to a
bias (an underestimate, indeed) in the final
![]() if the sample of stars is old enough to have experienced a not
negligible amount of diffusion of heavy elements; we will show this in
Sect. 5.2.
if the sample of stars is old enough to have experienced a not
negligible amount of diffusion of heavy elements; we will show this in
Sect. 5.2.
When generating the stellar models parameters for our sets of stars, we do not take into account any age-metallicity relation, hence [Fe/H] and age values are independently and randomly extracted. Recent works (Holmberg et al. 2007; Nordström et al. 2004) have indeed shown that there is no evidence of an age-metallicity relation for local disk stars. Given mass, age and chemical composition, we interpolated in our fine grid of stellar models to obtain the observational properties of the simulated stars. The number of stars in each simulated set is 110, a number comparable to the 103 stars of our real data sample. In the following and in the related figures, we will refer to the input parameters of our simulated samples using the subscript in and to the output of the recovery method using the subscript out.
5.1 The effect of measurements errors
The first test we have performed was made to check whether our recovery
method was able to get the right
![]() from an ``ideal'' sample of stars affected only by observational errors
on the magnitude, color and [Fe/H] values. By ideal we mean a sample
that, regardless of masses and [Fe/H] distribution (which indeed were
generated in a completely random fashion), contains only stars really
lying on the ZAMS. It is worth to point out that in the case
of the real data, this is only a simplifying assumption, which cannot
be exactly fulfilled, since the observed stars in our sample have
unknown ages that span the whole range of ages in the Galactic disk.
from an ``ideal'' sample of stars affected only by observational errors
on the magnitude, color and [Fe/H] values. By ideal we mean a sample
that, regardless of masses and [Fe/H] distribution (which indeed were
generated in a completely random fashion), contains only stars really
lying on the ZAMS. It is worth to point out that in the case
of the real data, this is only a simplifying assumption, which cannot
be exactly fulfilled, since the observed stars in our sample have
unknown ages that span the whole range of ages in the Galactic disk.
Once the artificial sample has been generated, we associated to each star an error in absolute magnitude, color and [Fe/H] typical of our real sample of data, i.e., 0.1 mag, 0.03 mag and 0.1 dex respectively (see Sect. 3) .
We found that our recovery method is not affected by
observational errors on this order of magnitude. As it is possible to
see in Fig. 4,
given a
![]() of 4, the best value that comes out from our Monte Carlo method and the
Gaussian fit to the histogram of occurrences is indeed
of 4, the best value that comes out from our Monte Carlo method and the
Gaussian fit to the histogram of occurrences is indeed
![]() .
So the outcome of the method is perfectly consistent with the input
value and; moreover it has a very narrow range of 1.26 at a level of
.
So the outcome of the method is perfectly consistent with the input
value and; moreover it has a very narrow range of 1.26 at a level of ![]() ,
which is comparable to the resolution in our models grid (1 unit), and
which we may quote as the nominal or intrinsic error of the method,
associated to the typical error of the actual data.
,
which is comparable to the resolution in our models grid (1 unit), and
which we may quote as the nominal or intrinsic error of the method,
associated to the typical error of the actual data.

|
Figure 4: Results of a test for a sample of 110 simulated stars lying on the ZAMS (see text for more details). Overplotted is the best-fit Gaussian. |
| Open with DEXTER | |
5.2 The effects of age and heavy elements diffusion

|
Figure 5:
Results of a test for a sample of 110 simulated stars not lying on the
ZAMS. Ages are uniformly distributed between 0 and 7 Gyr. The solid
line gives the result when heavy elements diffusion is taken into
account, while the dashed line corresponds to the case where [Fe/H]t
is equal to [Fe/H]
|
| Open with DEXTER | |
Although our stellar sample has been obtained by selecting very faint
stars (MV
> 6 mag, i.e.
![]() ,
the actual value depending on the chemical composition), we found that
evolutionary effects strongly affect the final result introducing a non
negligible bias. This is actually one of the most
important results of this work. Thus, one should be very careful in
properly taking into account the evolutionary effects, i.e. the
displacement from the ZAMS, when helium-to-metals enrichment ratio is
derived from the low MS fine structure.
,
the actual value depending on the chemical composition), we found that
evolutionary effects strongly affect the final result introducing a non
negligible bias. This is actually one of the most
important results of this work. Thus, one should be very careful in
properly taking into account the evolutionary effects, i.e. the
displacement from the ZAMS, when helium-to-metals enrichment ratio is
derived from the low MS fine structure.
Indeed, by creating artificial stellar data sets with
![]() ,
but no longer on their ZAMS position, we found an output
value of our recovery method of
,
but no longer on their ZAMS position, we found an output
value of our recovery method of
![]() .
The actual best-fit value for each simulated data set depends on the
exact
parameters used to generate the artificial sample, like the maximum age
or the
functional form of the age distribution (uniform or with an
exponentially
decaying SFR). The total number of stars, their [Fe/H] and magnitude
ranges
are always kept the same between the different simulated data set.
Figure 5
shows the results of our method using data sets where the simulated
stars have ages uniformly distributed between 0 and 7 Gyr. The
dashed line indicates the results when the [Fe/H] values associated to
each
star at a given age are the same as the ones at the ZAMS; whereas the
solid
line indicates the results when diffusion is taken into account, i.e.
the
value at a given time [Fe/H]t
is different from [Fe/H]
.
The actual best-fit value for each simulated data set depends on the
exact
parameters used to generate the artificial sample, like the maximum age
or the
functional form of the age distribution (uniform or with an
exponentially
decaying SFR). The total number of stars, their [Fe/H] and magnitude
ranges
are always kept the same between the different simulated data set.
Figure 5
shows the results of our method using data sets where the simulated
stars have ages uniformly distributed between 0 and 7 Gyr. The
dashed line indicates the results when the [Fe/H] values associated to
each
star at a given age are the same as the ones at the ZAMS; whereas the
solid
line indicates the results when diffusion is taken into account, i.e.
the
value at a given time [Fe/H]t
is different from [Fe/H]
![]() .
Even without taking into account diffusion, the method gives an output
value of
.
Even without taking into account diffusion, the method gives an output
value of
![]() ,
quite different from
,
quite different from
![]() .
When also diffusion is taken into account, the best fit value suffers
an additional shift, with
.
When also diffusion is taken into account, the best fit value suffers
an additional shift, with
![]() .
Since we don't know what is the real age distribution of the stars of
our sample we cannot really quantify the bias, but after many
experiments with several data set, we conclude that it must be on the
order of
.
Since we don't know what is the real age distribution of the stars of
our sample we cannot really quantify the bias, but after many
experiments with several data set, we conclude that it must be on the
order of
![]() .
.
The effect of evolution on the derived enrichment ratio is
easy to understand by looking at Fig. 6. Here two
ZAMS with different values of
![]() ,
namely 2 and 4, and same [Fe/H] = 0.0 are
shown together with isochrones of 1 and 7 Gyr, calculated with
,
namely 2 and 4, and same [Fe/H] = 0.0 are
shown together with isochrones of 1 and 7 Gyr, calculated with
![]() and
[Fe/H] = 0.0; it is clear that evolution causes a
shift of the whole curve towards redder colors
and
[Fe/H] = 0.0; it is clear that evolution causes a
shift of the whole curve towards redder colors![]() in a completely indistinguishable fashion as a lower
in a completely indistinguishable fashion as a lower
![]() does.
does.
As a summary, this means that, even if our observational
data set has been selected with a very strict cutoff of MV
= 6 mag, evolutionary effects still play an important role.
The real, unbiased value of
![]() coming out from our analisys has then to be corrected, by subtracting
coming out from our analisys has then to be corrected, by subtracting
![]() from the nominal value given by the Monte Carlo method. We then expect
that the real value is higher by about two units than what can be found
by blindly applying this method to the data.
from the nominal value given by the Monte Carlo method. We then expect
that the real value is higher by about two units than what can be found
by blindly applying this method to the data.

|
Figure 6:
The evolution of stars mimics lower values of the enrichment ratio. A
7 Gyr isochrone calculated for
|
| Open with DEXTER | |
5.3 The effects of the uncertainty on the mixing-length efficiency
The current generation of stellar models is not yet able to firmly
predict the effective temperature of stars with a convective envelope,
such as those belonging to our sample. The reason is that a
satisfactory and fully consistent theory of convection in
superadiabatic regimes is still lacking, hence a very simplified
approach is usually followed. The approach commonly adopted in the vast
majority of evolutionary codes is to
implement the mixing-length theory (Böhm-Vitense
1958), in which the average efficiency of convective energy
transport depends on a free parameter ![]() that must be calibrated. Our reference set of stellar models has been
computed adopting our solar calibrated value of the mixing length
parameter, namely
that must be calibrated. Our reference set of stellar models has been
computed adopting our solar calibrated value of the mixing length
parameter, namely ![]() .
Nevertheless, we calculated a whole new grid of models using
.
Nevertheless, we calculated a whole new grid of models using
![]() in order to evaluate the effect of this still uncertain parameter on
the derived value of
in order to evaluate the effect of this still uncertain parameter on
the derived value of ![]() .
As well known, the predicted effective temperature of a stellar model
with a convective envelope is an increasing function of the value of
the mixing length parameter
.
As well known, the predicted effective temperature of a stellar model
with a convective envelope is an increasing function of the value of
the mixing length parameter ![]() ,
as a consequence of the shallower temperature gradient due to a more
efficient convective energy transfer.
,
as a consequence of the shallower temperature gradient due to a more
efficient convective energy transfer.
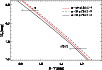
Figure 7
shows the effect of different adopted ![]() values on the calculated ZAMS. The assumed mixing-length parameter
affects also the inferred
values on the calculated ZAMS. The assumed mixing-length parameter
affects also the inferred
![]() ratio, since it directly influences the predicted position in the HR
diagram of the ZAMS models. As one can easily see in Fig. 7, in order to
recover the ZAMS locus of models computed with an higher value of
ratio, since it directly influences the predicted position in the HR
diagram of the ZAMS models. As one can easily see in Fig. 7, in order to
recover the ZAMS locus of models computed with an higher value of ![]() ,
a lower
,
a lower ![]() ratio is needed. Notice also that, the impact of the mixing-length
efficiency on the predicted effective temperature of ZAMS models of the
same chemical composition becomes progressively smaller at faint
magnitudes, i.e. for very low-masses. Such a behavior is the
consequence of the almost adiabatic nature of convection in the
envelopes of very-low mass stars (
ratio is needed. Notice also that, the impact of the mixing-length
efficiency on the predicted effective temperature of ZAMS models of the
same chemical composition becomes progressively smaller at faint
magnitudes, i.e. for very low-masses. Such a behavior is the
consequence of the almost adiabatic nature of convection in the
envelopes of very-low mass stars (
![]() ),
characterized by high densities and low temperatures.
),
characterized by high densities and low temperatures.
|
Figure 7:
Effect of changing the mixing length parameter from
|
| Open with DEXTER | |
Since an increase in ![]() affects the models in the same direction as an increase in
affects the models in the same direction as an increase in
![]() ,
we find, as expected, that our recovery
method gives a lower value of the enrichment ratio when ZAMS calculated
for
,
we find, as expected, that our recovery
method gives a lower value of the enrichment ratio when ZAMS calculated
for
![]() are used, that is,
are used, that is,
![]() ,
quite different from
,
quite different from
![]() .
This is shown in Fig. 8
which reports the output of the Monte Carlo method, when the same data
set of Sect. 5.1
is used, i.e. a set of stars lying on the ZAMS calculated with
.
This is shown in Fig. 8
which reports the output of the Monte Carlo method, when the same data
set of Sect. 5.1
is used, i.e. a set of stars lying on the ZAMS calculated with
![]() .
We already
mentioned that the use of the solar calibration should be the safer
choice when dealing with Main Sequence stars of solar-like masses such
those of our data set. On the other hand, this numeric experiment
allows the quantification of the effects of a wrong assumption of the
mixing length parameter in the adopted stellar models on the inferred
helium-to-metals enrichment ratio.
.
We already
mentioned that the use of the solar calibration should be the safer
choice when dealing with Main Sequence stars of solar-like masses such
those of our data set. On the other hand, this numeric experiment
allows the quantification of the effects of a wrong assumption of the
mixing length parameter in the adopted stellar models on the inferred
helium-to-metals enrichment ratio.

|
Figure 8:
Results for the same data set of Fig.4.
In this case we ran our Monte Carlo method using ZAMS calculated with a
mixing length parameter |
| Open with DEXTER | |
5.4 The effects of different transformations from the theoretical to the observational plane
To compare observational data with stellar models, one needs to
transform the theoretical predictions of evolutionary codes from the
![]() plane (HR diagram) to the observational plane, in our case the
plane (HR diagram) to the observational plane, in our case the
![]() Color-Magnitude diagram.
A common procedure is to use synthetic stellar spectra, calculated
using model atmosphere codes, and to convolve them with the filter
throughput of the photometric system needed; this technique, referred
to as synthetic photometry is described in detail
in, e.g. Girardi et al.
(2002).
We transformed our models using PHOENIX (Brott
et al. 2005) and ATLAS9 (Castelli
& Kurucz 2003) model atmospheres; the UBVRIJHKL
Johnson-Cousin-Glass photometric system zero points are those of
Table A1 in Bessel
et al. (1999).
Color-Magnitude diagram.
A common procedure is to use synthetic stellar spectra, calculated
using model atmosphere codes, and to convolve them with the filter
throughput of the photometric system needed; this technique, referred
to as synthetic photometry is described in detail
in, e.g. Girardi et al.
(2002).
We transformed our models using PHOENIX (Brott
et al. 2005) and ATLAS9 (Castelli
& Kurucz 2003) model atmospheres; the UBVRIJHKL
Johnson-Cousin-Glass photometric system zero points are those of
Table A1 in Bessel
et al. (1999).
Both model atmosphere grids completely cover our range of
![]() and [Fe/H]. An exhaustive description of these models is far beyond the
scope of this paper, nevertheless we want to mention briefly some of
the most important differences between them.
The ATLAS9 code solves the radiative transfer equation in a plane
parallel atmosphere, while PHOENIX code takes into account the
curvature of the atmosphere, even though in spherical symmetry, i.e.
keeping a 1D approach. This difference is not very important for dwarf
stars, for which the curvature (i.e. the ratio of the extent of the
atmosphere to the radius of the base of the atmosphere) is very low.
More important is the different database of molecular opacities for the
two models. While atomic opacities databases are similar between the
two models, PHOENIX models include a lot of molecular species (
and [Fe/H]. An exhaustive description of these models is far beyond the
scope of this paper, nevertheless we want to mention briefly some of
the most important differences between them.
The ATLAS9 code solves the radiative transfer equation in a plane
parallel atmosphere, while PHOENIX code takes into account the
curvature of the atmosphere, even though in spherical symmetry, i.e.
keeping a 1D approach. This difference is not very important for dwarf
stars, for which the curvature (i.e. the ratio of the extent of the
atmosphere to the radius of the base of the atmosphere) is very low.
More important is the different database of molecular opacities for the
two models. While atomic opacities databases are similar between the
two models, PHOENIX models include a lot of molecular species (![]() 650) and
molecular transitions (
650) and
molecular transitions (![]() 550 millions)
which play an important role for low mass stars, specially as the
metallicity increases.
550 millions)
which play an important role for low mass stars, specially as the
metallicity increases.
Figure 9
shows the comparison between ZAMS models transformed using the two sets
of model atmosphere. It is evident how the PHOENIX ZAMS are always
redder in the B-V color than the
ATLAS9 ones at fixed magnitude. Moreover the differences in stellar
colors increase with decreasing mass (increasing magnitude) and also,
at a given magnitude, the differences increase with increasing
metallicity (from left to right in Fig. 9). Note that
both a lower temperature and a higher metal content favor the formation
of chemical composites; in particular the first molecules start forming
when the effective temperatures drops below ![]() 4000 K.
4000 K.
The sizeable difference in magnitude and color index between
the same theoretical ZAMS transformed into the observational plane by
the two quoted model atmospheres, directly translates into a large
difference in the inferred
![]() value. We used the ATLAS9 ZAMS, running our recovery method on a
simulated data set with
value. We used the ATLAS9 ZAMS, running our recovery method on a
simulated data set with
![]() but generated using the PHOENIX ZAMS. The ATLAS9 ZAMS are so much bluer
than the PHOENIX ones that in each iteration of the method we always
find the lowest possible value of
but generated using the PHOENIX ZAMS. The ATLAS9 ZAMS are so much bluer
than the PHOENIX ones that in each iteration of the method we always
find the lowest possible value of
![]() available in our grid of models, i.e. 0.5.
available in our grid of models, i.e. 0.5.
The uncertainty due to the chosen model atmosphere is then by far the most severe source of uncertainty affecting the final value of the enrichment ratio, at least among the uncertainties coming from the models side.
5.5 The effects of different choices for the heavy elements mixture

|
Figure 9:
ZAMS transformed into the observational plane using PHOENIX (solid
lines) and ATLAS9 (dashed lines) model atmospheres. All the ZAMS shown
have been calculated with
|
| Open with DEXTER | |
As previously explained, all the models in our grid have been
calculated using the solar-scaled mixture by Asplund
et al. (2005), hereafter AGS05.
A new version of the solar mixture has been recently published by the
same group in Asplund et al.
(2009), hereafter AGSS09.
The true dependence of the inferred
![]() on the mixture choice could be
evaluated only by re-calculating an equivalent grid of models using the
new
mixture and by re-running the whole procedure illustrated in this work.
However,
the exact determination of the solar mixture is still an open problem,
thus a
recalculation of all the models is not needed, in our opinion, until
this issue
will be definitively settled. Nevertheless, to have an idea of the
influence of a variation
of the solar mixture on our results, we computed two new sets of ZAMS
with different mixtures and compared them with our reference AGS05 ZAMS
in the CMD.
This gives at least an indication of how the inferred enrichment ratio
may depend on the mixture.
In addition to the ZAMS for AGS05 and AGSS09 mixtures, we also computed
and compared ZAMS
calculated with the older mixture by Grevesse
& Noels (1993), hereafter GN93, still widely used in
the literature.
We highlight the fact that we can control the effect of the mixture
changes
on the stellar structure, by using opacity tables calculated with
different
mixtures both for the high-temperature (OPAL) and low-temperature
(Ferguson et al. 2005)
opacities. On the other hand we cannot evaluate the effects of
different mixtures on the model atmosphere, i.e. on the transformation
of our
theoretical models from the theoretical HR diagram to the CMD, since
PHOENIX synthetic
spectra are available only for a single mixture of heavy elements.
on the mixture choice could be
evaluated only by re-calculating an equivalent grid of models using the
new
mixture and by re-running the whole procedure illustrated in this work.
However,
the exact determination of the solar mixture is still an open problem,
thus a
recalculation of all the models is not needed, in our opinion, until
this issue
will be definitively settled. Nevertheless, to have an idea of the
influence of a variation
of the solar mixture on our results, we computed two new sets of ZAMS
with different mixtures and compared them with our reference AGS05 ZAMS
in the CMD.
This gives at least an indication of how the inferred enrichment ratio
may depend on the mixture.
In addition to the ZAMS for AGS05 and AGSS09 mixtures, we also computed
and compared ZAMS
calculated with the older mixture by Grevesse
& Noels (1993), hereafter GN93, still widely used in
the literature.
We highlight the fact that we can control the effect of the mixture
changes
on the stellar structure, by using opacity tables calculated with
different
mixtures both for the high-temperature (OPAL) and low-temperature
(Ferguson et al. 2005)
opacities. On the other hand we cannot evaluate the effects of
different mixtures on the model atmosphere, i.e. on the transformation
of our
theoretical models from the theoretical HR diagram to the CMD, since
PHOENIX synthetic
spectra are available only for a single mixture of heavy elements.

|
Figure 10:
ZAMS calculated for the three different mixtures, GN93, AGS05 and
AGSS09, with |
| Open with DEXTER | |
The effect of the adopted solar mixture on the models is twofold.
First, for a given global metallicity Z,
changing the internal distribution of metals will
mainly affect the opacity and the nuclear burning efficiency (via the
CNO
abundances). For models with the same Y and Z,
the ZAMS computed with the
GN93 mixture are bluer than that with the AGSS09 one, which, in turn,
is bluer than the
ZAMS computed with the AGS05 mixture (see e.g. Degl'Innocenti et al. 2006;
Tognelli
et al. 2010). Second, for a given choice of the two
values of ![]() and
[Fe/H], it is clear from the coupled Eqs. (1) and 2) that the values
of Y and Z will be different,
given the different values of
and
[Fe/H], it is clear from the coupled Eqs. (1) and 2) that the values
of Y and Z will be different,
given the different values of
![]() .
More in detail, the GN93 mixture provides models with higher Z.
These models are thus redder on the CMD, than those calculated with
AGSS09 mixture. The latter mixture, in turn, provides models
that have higher Z and appear redder than the AGS05
mixture. Thus, the effects on the opacity and on the scaling, i.e. the
actual value of Z given [Fe/H] and the different
.
More in detail, the GN93 mixture provides models with higher Z.
These models are thus redder on the CMD, than those calculated with
AGSS09 mixture. The latter mixture, in turn, provides models
that have higher Z and appear redder than the AGS05
mixture. Thus, the effects on the opacity and on the scaling, i.e. the
actual value of Z given [Fe/H] and the different
![]() ,
affect the ZAMS position in opposite directions.
,
affect the ZAMS position in opposite directions.
We calculated models for the two additional mixtures by fixing
![]() and
choosing the two values
and
choosing the two values
![]() and 0.2.
The results of the calculations are shown in Fig. 10.
The corresponding Y and Z
values for each mixture are shown in Table 2 where also the
corresponding
and 0.2.
The results of the calculations are shown in Fig. 10.
The corresponding Y and Z
values for each mixture are shown in Table 2 where also the
corresponding
![]() values
are indicated. From Fig. 10 one can see
that GN93 models seem to be slightly redder than our reference AGS05
models; when
compared to observational data, an higher value of
values
are indicated. From Fig. 10 one can see
that GN93 models seem to be slightly redder than our reference AGS05
models; when
compared to observational data, an higher value of
![]() would
then
be needed to reproduce observations, as compared to the AS05 mixture.
AGSS09 ZAMS go in the opposite direction meaning that the inferred
value of the enrichment ratio would be lower when compared to AGS05.
In the comparison between AGS05 and AGSS09, which have quite similar
would
then
be needed to reproduce observations, as compared to the AS05 mixture.
AGSS09 ZAMS go in the opposite direction meaning that the inferred
value of the enrichment ratio would be lower when compared to AGS05.
In the comparison between AGS05 and AGSS09, which have quite similar
![]() ,
the effect on the opacity and burning efficiency seems to
prevail on the scaling; viceversa in the comparison between AGS05
and GN93, the huge difference in
,
the effect on the opacity and burning efficiency seems to
prevail on the scaling; viceversa in the comparison between AGS05
and GN93, the huge difference in
![]() compensates for the opacity
effect, and the much higher Z value in the
GN93 case brings the ZAMS models toward redder colors when compared to
AGS05.
compensates for the opacity
effect, and the much higher Z value in the
GN93 case brings the ZAMS models toward redder colors when compared to
AGS05.
The relative behavior of different ZAMS is moreover a non
trivial function of the actual value of [Fe/H], given the non linear
relation between the two couples of values
![]() ,
represented by the two Eqs. (1) and (2).
Overall it seems that changing the mixture affects our method in a non
negligible way, but a totally consistent check could be done only when
the appropriate model atmospheres are used to do the transformation
from the HR diagram to the CMD and only calculating complete grids of
models for different mixtures.
,
represented by the two Eqs. (1) and (2).
Overall it seems that changing the mixture affects our method in a non
negligible way, but a totally consistent check could be done only when
the appropriate model atmospheres are used to do the transformation
from the HR diagram to the CMD and only calculating complete grids of
models for different mixtures.
Table 2:
Y and Z values for the three
different adopted mixtures (see text in Sect. 5.5),
for two reference values of [Fe/H] and
![]() .
.
6 Results using the observational data
After having carefully checked the capability of our recovery method and having studied many uncertainty sources by means of controlled artificial data sets, we applied the above technique on the sample of real observational data described in Sect. 3.
Figure 3
shows the result of the Monte Carlo recovery method applied to the
local low-MS field stars, which provides a nominal value of the
enrichment ratio of
![]() .
.
This result for the enrichment ratio is obtained using our
favorite set of
models, i.e. ZAMS calculated with the solar
![]() and transformed using the PHOENIX model atmospheres.
We showed in Sects. 5.3 and 5.4 the significative effects on
the inferred
helium-to-metals enrichment ratio of a different choice of the mixing
length parameter
and transformed using the PHOENIX model atmospheres.
We showed in Sects. 5.3 and 5.4 the significative effects on
the inferred
helium-to-metals enrichment ratio of a different choice of the mixing
length parameter ![]() and of the model atmosphere, respectively, in the
case of synthetic data. The recovery procedure applied to the real
observational data provides a nominal value of the enrichment ratio of
and of the model atmosphere, respectively, in the
case of synthetic data. The recovery procedure applied to the real
observational data provides a nominal value of the enrichment ratio of
![]() adopting the set of theoretical models computed
with
adopting the set of theoretical models computed
with ![]() and transformed into the observational plane by means of
PHOENIX atmosphere models and
and transformed into the observational plane by means of
PHOENIX atmosphere models and
![]() adopting our standard set of models with
adopting our standard set of models with
![]() but the ATLAS9 atmosphere models.
but the ATLAS9 atmosphere models.
Moreover, we will show a self-consistency check in
Sect. 8,
to prove that inside our choice the result we
obtain for ![]() can be used to calculate models that fit very well an independent data
set, in particular the Hyades main sequence.
can be used to calculate models that fit very well an independent data
set, in particular the Hyades main sequence.
In Sect. 3
we mentioned the fact that the fit of a Gaussian distribution to the
histogram of occurrences of Fig. 3 is not
perfect. The actual distribution looks quite flat in the range
![]() and the
and the ![]() of the fitting Gaussian is twice as big as what we would expect from
the observational uncertainties alone (see Sect. 5.1).
We also mentioned that our [Fe/H] estimates come from two different
catalogs, and that the N04 data have been re-zeroed according to T05
transformations. Nevertheless, when considering the two subsets of data
separately, a large difference in the final result is still visible, as
if the different [Fe/H] scale adopted, even after the re-zeroing, would
mimic a bimodal chemical composition distribution.
From Fig. 11
it is clear that the two results for the separate
subsets are inconsistent at
of the fitting Gaussian is twice as big as what we would expect from
the observational uncertainties alone (see Sect. 5.1).
We also mentioned that our [Fe/H] estimates come from two different
catalogs, and that the N04 data have been re-zeroed according to T05
transformations. Nevertheless, when considering the two subsets of data
separately, a large difference in the final result is still visible, as
if the different [Fe/H] scale adopted, even after the re-zeroing, would
mimic a bimodal chemical composition distribution.
From Fig. 11
it is clear that the two results for the separate
subsets are inconsistent at ![]() level. The final result we get for the
whole set, is then an average of the two distributions of
Fig. 11;
unfortunately this method is quite sensitive to the adopted scale of
[Fe/H] determinations. We won't choose any of the two subsets as the best
one, we just state that systematics is probably still
affecting the [Fe/H] of our objects, even after the correction of N04
zero point.
Anyway, in order to proceed further with the analysis we will use the
results of the Gaussian fit to the histogram of occurrences for the
whole sample of data as our nominal value for
level. The final result we get for the
whole set, is then an average of the two distributions of
Fig. 11;
unfortunately this method is quite sensitive to the adopted scale of
[Fe/H] determinations. We won't choose any of the two subsets as the best
one, we just state that systematics is probably still
affecting the [Fe/H] of our objects, even after the correction of N04
zero point.
Anyway, in order to proceed further with the analysis we will use the
results of the Gaussian fit to the histogram of occurrences for the
whole sample of data as our nominal value for
![]() .
As we showed in Sect. 5.2, to
obtain the real
.
As we showed in Sect. 5.2, to
obtain the real ![]() value, the nominal value of
value, the nominal value of
![]() provided by the recovery method must be corrected for the age-bias,
i.e. the artificial shift in the recovered value of the enrichment
ratio caused by neglecting evolutionary effects and diffusion. We
estimated the extent of such a correction to be of
provided by the recovery method must be corrected for the age-bias,
i.e. the artificial shift in the recovered value of the enrichment
ratio caused by neglecting evolutionary effects and diffusion. We
estimated the extent of such a correction to be of
![]() by means of Monte Carlo simulations. Thus, the final corrected value of
the helium-to-metals enrichment, combining the errors in quadrature is
by means of Monte Carlo simulations. Thus, the final corrected value of
the helium-to-metals enrichment, combining the errors in quadrature is
![]() .
.
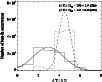
|
Figure 11: Results of our Monte Carlo method when applied separately to the subsets of objects with [Fe/H] from T05 and N04 (the latter corrected using Table 10 of T05). The solid lines are for T05, the dashed for N04. Overplotted are the best-fit Gaussians. |
| Open with DEXTER | |
7 A possible non-linear relation between Y and Z?
In their recent work, Casagrande
et al. (2007) suggested that the assumption of a
linear relation between metals and helium enrichment of the ISM, which
leads to the definition of the enrichment ratio itself (see
Eq. (1))
may not necessarily be valid.
We tried to check whether it is possible to unambiguously infer such a
non linear behavior from the presently available data accurateness. We
performed the test by means of an artificial and controlled data set
built interpolating our stellar models. The synthetic stellar sample
mimics the main characteristics of the real data set. In particular, we
simulated stars divided in metallicity bins 0.1 dex wide in
the range [Fe/H] ![]() ,
with the same number of stars in each bin as our observational data,
for a total number of 103 objects. To avoid the additional
difficulties introduced by the age-bias, the simulated stars were taken
on their ZAMS position.
We then ran our Monte Carlo method bin by bin to see whether our
recovery is able to recover the input value for
,
with the same number of stars in each bin as our observational data,
for a total number of 103 objects. To avoid the additional
difficulties introduced by the age-bias, the simulated stars were taken
on their ZAMS position.
We then ran our Monte Carlo method bin by bin to see whether our
recovery is able to recover the input value for
![]() in each bin, given the typical observational errors on our objects.
in each bin, given the typical observational errors on our objects.
Figure 12
shows the outcome of such an experiment. On the two panels each point
represents the result of the Monte Carlo method when applied to the
corresponding [Fe/H] bin, with its 1![]() uncertainty; both values come from the Gaussian fitting of the
histogram of occurrences. The dashed lines represent the results of the
Gaussian fit the histogram of occurrences when the method is applied to
the whole sample of simulated stars; the shaded area corresponds to the
1
uncertainty; both values come from the Gaussian fitting of the
histogram of occurrences. The dashed lines represent the results of the
Gaussian fit the histogram of occurrences when the method is applied to
the whole sample of simulated stars; the shaded area corresponds to the
1![]() uncertainty around the mean. The two panels represent results for two
different ways of binning the data; on the left panel we show the
results when data are binned in 0.1 dex wide non overlapping
bins; on the right panel the results are for 0.2 dex wide
bins, in this case adjacent bins have an overlap of 0.1 dex,
meaning e.g. that a [Fe/H] = -0.35 star can be found
in both the [-0.5, -0.3] and the [-0.4, -0.2] bins.
Regardless from the way the binning is performed, it follows from this
numerical experiment that the method works fine only for [Fe/H] values
equal or greater than -0.3 dex.
uncertainty around the mean. The two panels represent results for two
different ways of binning the data; on the left panel we show the
results when data are binned in 0.1 dex wide non overlapping
bins; on the right panel the results are for 0.2 dex wide
bins, in this case adjacent bins have an overlap of 0.1 dex,
meaning e.g. that a [Fe/H] = -0.35 star can be found
in both the [-0.5, -0.3] and the [-0.4, -0.2] bins.
Regardless from the way the binning is performed, it follows from this
numerical experiment that the method works fine only for [Fe/H] values
equal or greater than -0.3 dex.
![]() determinations with this method, considering only lower values of the
metallicity are unreliable. The missing points in the two panel,
correspond to bins where the Gaussian fit failed, simply because the
histogram of occurrences is too irregular to be fitted by a Gaussian.
determinations with this method, considering only lower values of the
metallicity are unreliable. The missing points in the two panel,
correspond to bins where the Gaussian fit failed, simply because the
histogram of occurrences is too irregular to be fitted by a Gaussian.
Hence any discussion of a possible non linearity of the
helium-to-metals enrichment relation, extending over a wide range of
metallicities, cannot be carried on when Y and Z
value are determined from low-main sequence fitting. The fine structure
of the low main sequence at values of the metallicity lower than -0.3
dex is indeed too weakly dependent on the chemical composition, to be
used to infer any non linear behavior of the ISM enrichment in helium
and metals.
This is quite clear from the right panel of Fig. 2, which
shows that the separation among curves with different
![]() becomes progressively smaller and smaller as the [Fe/H] decreases. At
low enough values of [Fe/H], this separation is simply too small with
respect to the spread of the observed point, due to the current
uncertainties in both magnitudes and [Fe/H], which are on the order of
0.1 mag and 0.1 dex respectively, to allow a correct determination of
the stars chemical composition. This uncertainty is reflected in the
large error bars of the lower metallicity bins of Fig. 12.
becomes progressively smaller and smaller as the [Fe/H] decreases. At
low enough values of [Fe/H], this separation is simply too small with
respect to the spread of the observed point, due to the current
uncertainties in both magnitudes and [Fe/H], which are on the order of
0.1 mag and 0.1 dex respectively, to allow a correct determination of
the stars chemical composition. This uncertainty is reflected in the
large error bars of the lower metallicity bins of Fig. 12.
We are not claiming that any non linear law for the helium-to-metals enrichment of the ISM must be ruled out; we are just stating that better data are needed to confirm this possibility by making use of the fine structure of the low main sequence. The GAIA mission will provide us with better parallaxes, which will yield better absolute magnitude determinations. Advances in 3D and NLTE stellar atmospheres modeling will also produce better constrained spectroscopic abundances determinations in the future.
![\begin{figure}
\par\includegraphics[width=17cm]{14227f12.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14227-10/Timg95.png)
|
Figure 12:
Output values of the recovery method when data are binned in
metallicity (see text for details). The green dashed lines represent
the |
| Open with DEXTER | |
8 The Hyades test
As previously discussed, the
![]() provided by the recovery procedure must be corrected for the age-bias,
since the above described technique uses the theoretical ZAMS loci as
reference mile stones in the CMD. Hence, any unaccounted displacements
of the observed stars from the ZAMS due to evolutionary effects
translates directly in an underestimate of the inferred
provided by the recovery procedure must be corrected for the age-bias,
since the above described technique uses the theoretical ZAMS loci as
reference mile stones in the CMD. Hence, any unaccounted displacements
of the observed stars from the ZAMS due to evolutionary effects
translates directly in an underestimate of the inferred
![]() .
Clearly, the younger the stellar sample analyzed, the smaller such
unaccounted displacements and the smaller the related age-bias.
.
Clearly, the younger the stellar sample analyzed, the smaller such
unaccounted displacements and the smaller the related age-bias.
To safely neglect any possible bias due to evolution, we also
applied our recovery method to a very young stellar sample: the stars
of the lowest part (
![]() )
of the Hyades MS. For this well studied cluster an age of about
)
of the Hyades MS. For this well studied cluster an age of about
![]() Myr
is generally estimated (see e.g. Castellani et al. 2002,2001;
Perryman
et al. 1998). Thus, the selected low luminosity
stars, which correspond to masses lower than about
Myr
is generally estimated (see e.g. Castellani et al. 2002,2001;
Perryman
et al. 1998). Thus, the selected low luminosity
stars, which correspond to masses lower than about
![]() ,
are really on, or at least very close to, their ZAMS position.
Moreover, the data available for this cluster are even more precise
than those of our data set for field stars in the solar neighborhood;
using the kinematically corrected parallaxes data from Madsen, Dravins & Lindegren (2002)
the typical errors are
,
are really on, or at least very close to, their ZAMS position.
Moreover, the data available for this cluster are even more precise
than those of our data set for field stars in the solar neighborhood;
using the kinematically corrected parallaxes data from Madsen, Dravins & Lindegren (2002)
the typical errors are
![]() and
and ![]() .
The metallicity value we use for the Hyades is taken from Perryman et al. (1998):
[Fe/H] =
.
The metallicity value we use for the Hyades is taken from Perryman et al. (1998):
[Fe/H] = ![]() .
.
By running our Monte Carlo method, the value found for the
enrichment ratio is
![]() ,
in perfect agreement with what we found using local MS stars and taking
into account the evolutionary bias.
,
in perfect agreement with what we found using local MS stars and taking
into account the evolutionary bias.
To further check the consistency of this final result, we
calculated isochrones using the closest value of the enrichment ratio
in our grid, i.e. ![]() ,
and for the extreme values of Perryman
et al. (1998) [Fe/H] interval, i.e. 0.09 and
0.19 dex.
Models are calculated for our solar calibrated value of the mixing
length parameter and transformed to the observational plane using
PHOENIX model atmosphere.
Average extinction towards the Hyades is negligible and this cluster is
old enough not to present any intra-cluster material, so also
differential extinction can be ignored; hence we assume
,
and for the extreme values of Perryman
et al. (1998) [Fe/H] interval, i.e. 0.09 and
0.19 dex.
Models are calculated for our solar calibrated value of the mixing
length parameter and transformed to the observational plane using
PHOENIX model atmosphere.
Average extinction towards the Hyades is negligible and this cluster is
old enough not to present any intra-cluster material, so also
differential extinction can be ignored; hence we assume
![]() .
.
Figure 13
shows the CMD of the Hyades with overimposed our isochrones.
The good agreement between our models with the chemical composition
derived by the recovery method and the Hyades data is quite encouraging
and make us confident about the adopted procedure.
Even more important is that the fit to the Hyades MS is good also at
higher luminosities. Stars with
![]() (corresponding to a magnitude
(corresponding to a magnitude
![]() ,
the exact value depending on chemical composition and age) have
essentially radiative envelopes, meaning that their predicted
temperatures are not affected by the choice on the mixing length
parameter,
,
the exact value depending on chemical composition and age) have
essentially radiative envelopes, meaning that their predicted
temperatures are not affected by the choice on the mixing length
parameter, ![]() .
.

|
Figure 13: The CMD for the Hyades Main Sequence. Isochrones for two values of the age are overplotted: 500 Myr (black lines) and 600 Myr (red lines). Dashed and solid lines correspond to two different values of the chemical composition. Y and Z values are obtained from Equations (1) and (2) using [Fe/H] = 0.09 dex (dashed lines) and [Fe/H] = 0.19 dex (solid lines). |
| Open with DEXTER | |
9 Comparison with independent methods
Many independent approaches have been followed in the past to determine
the helium-to-metals enrichment ratio. A detailed comparison between
the value of helium-to-metal enrichment ratio
![]() obtained by means of different techniques is beyond the aim of the
paper, since it would require a careful discussion of the different
uncertainty sources, both systematics and random, affecting the various
techniques. Furthermore, the primordial helium abundance
obtained by means of different techniques is beyond the aim of the
paper, since it would require a careful discussion of the different
uncertainty sources, both systematics and random, affecting the various
techniques. Furthermore, the primordial helium abundance ![]() adopted by different authors and/or in different periods can be very
different, affecting the inferred
adopted by different authors and/or in different periods can be very
different, affecting the inferred
![]() value. On the other hand, we think that a brief description of the
results provided by different approaches might be of interest.
value. On the other hand, we think that a brief description of the
results provided by different approaches might be of interest.
One of the most fruitful consists in observing
HII regions in the Milky Way
and in other galaxies. The pioneering papers by Peimbert & Torres-Peimbert (1976,1974)
and by Lequeux et al. (1979),
devoted respectively to the HII regions in the Magellanic
Clouds
and in irregular and blue compact galaxies, derived a value of the
helium to metals enrichment ratio of
![]() .
From observations of extragalactic HII regions, Pagel
et al. (1992) found that
.
From observations of extragalactic HII regions, Pagel
et al. (1992) found that
![]() ,
with a preferred value close to 4, while
Peimbert et al. (2000)
obtained
,
with a preferred value close to 4, while
Peimbert et al. (2000)
obtained
![]() from NGC346, the brightest HII region in SMC. A detailed study of a
copious sample of spectroscopic observations of HII regions in blue
compact galaxies performed by Izotov
& Thuan (2004) led to
from NGC346, the brightest HII region in SMC. A detailed study of a
copious sample of spectroscopic observations of HII regions in blue
compact galaxies performed by Izotov
& Thuan (2004) led to
![]() .
However, a reanalysis of the same data by Fukugita
& Kawasaki (2006) provides
.
However, a reanalysis of the same data by Fukugita
& Kawasaki (2006) provides
![]() ,
values that becomes as low as 1.1
,
values that becomes as low as 1.1![]() 1 if stellar absorption is taken into account.
1 if stellar absorption is taken into account.
From observations of galactic HII regions, such as
the Orion nebula, M8 and M17, various
authors found ![]() (see also Esteban
et al. 1999; Deharveng et al. 2000).
As an example Peimbert
et al. (2000) found
(see also Esteban
et al. 1999; Deharveng et al. 2000).
As an example Peimbert
et al. (2000) found
![]() adopting
a temperature fluctuation parameter t2=0.037
(recommended) and
adopting
a temperature fluctuation parameter t2=0.037
(recommended) and ![]() adopting t2=0.000. More
recently, Balser (2006)
derived
adopting t2=0.000. More
recently, Balser (2006)
derived
![]() from the analysis of the sole M17 and S206, whereas taking
into account also the HII regions belonging to the Magellanic Clouds
and metal-poor galaxies, she found
from the analysis of the sole M17 and S206, whereas taking
into account also the HII regions belonging to the Magellanic Clouds
and metal-poor galaxies, she found
![]() .
The
last author warns also on the systematic underestimation of the
measured helium abundance caused by a clumping in HII regions
(see also Mathis & Wood 2005).
Finally, a new estimate of the chemical composition of M17 by Carigi & Peimbert (2008)
yields
.
The
last author warns also on the systematic underestimation of the
measured helium abundance caused by a clumping in HII regions
(see also Mathis & Wood 2005).
Finally, a new estimate of the chemical composition of M17 by Carigi & Peimbert (2008)
yields
![]() and
and ![]() adopting
t2=0.036 and 0.000,
respectively.
adopting
t2=0.036 and 0.000,
respectively.
A useful technique to empirically constrain the stellar helium
to heavier
elements enrichment ratio is the analysis of the chemical composition
of planetary nebulae (PNe). These objects present the
advantage of being
numerous in a wide range of metallicity and of allowing precise
estimates of helium abundance.
On the other hand, it is a well established result of stellar evolution
that
the chemical composition of low and intermediate mass stars, i.e. the
PNe's
progenitors, is strongly modified by the dredge-up episodes, which
enrich the envelope with inner material previously processed by nuclear
reactions,
that is mainly with fresh helium and, in the case of III dredge-up in
thermally
pulsating AGB stars, also with heavier elements, mainly carbon. Thus,
the chemical composition of PNe is not representative of the
protostellar cloud and in order to derive the original interstellar
abundances a correction must be applied which takes into account the
evolution of the surface abundances of the progenitor star. In the
early attempts to determine the
![]() ratio using the
PNe in the late '70 s, such a correction was neglected and
values in the range 2.2-3.6 were obtained (see e.g. Dodorico
et al. 1976; Peimbert & Serrano 1980).
In our knowledge, Chiappini
& Maciel (1994) were the first to take into account
the correction due to the evolution of the progenitor star and
they obtained
ratio using the
PNe in the late '70 s, such a correction was neglected and
values in the range 2.2-3.6 were obtained (see e.g. Dodorico
et al. 1976; Peimbert & Serrano 1980).
In our knowledge, Chiappini
& Maciel (1994) were the first to take into account
the correction due to the evolution of the progenitor star and
they obtained
![]() .
More recently, Maciel (2001)
found
.
More recently, Maciel (2001)
found ![]() adopting
adopting
![]() and
and ![]() with
with ![]() .
.
An important independent constraint on the stellar helium to
heavier
elements enrichment ratio is provided by the Sun, for which very
detailed and
accurate data are available. In order to derive the
![]() ratio
from
the Sun, the precise spectroscopic estimates of the solar
photospheric chemical composition are not enough because they
significantly differ from the original ones due to diffusion and
gravitational settling. Thus, one has to rely on a standard solar model
(SSM), that is, a stellar model of 1
ratio
from
the Sun, the precise spectroscopic estimates of the solar
photospheric chemical composition are not enough because they
significantly differ from the original ones due to diffusion and
gravitational settling. Thus, one has to rely on a standard solar model
(SSM), that is, a stellar model of 1
![]() which at the age of the Sun
(i.e.
which at the age of the Sun
(i.e. ![]() 4.56 Gyr)
fits the
solar observables. As a result of such a procedure, the initial
metallicity
4.56 Gyr)
fits the
solar observables. As a result of such a procedure, the initial
metallicity
![]() and helium
and helium
![]() abundance are inferred. As largely debated
in recent years (see e.g Bahcall et al. 2005b; Basu & Antia
2008; Serenelli
et al. 2009; Christensen-Dalsgaard et al.
2009, and references therein), the very good agreement
between the SSM and the helioseismological constraints, mainly the
sound speed profile, the extension
of the convective envelope and the surface helium abundance, achieved
at the end of the last century has been compromised by the new
determinations of the metal abundances based on 3D photospheric models
by Asplund et al. (2005),
and only slightly alleviated by the very recent release by Asplund et al. (2009).
With these caveats, the initial helium and metal abundance of the Sun
provided
by the current SSMs allow determination of the
abundance are inferred. As largely debated
in recent years (see e.g Bahcall et al. 2005b; Basu & Antia
2008; Serenelli
et al. 2009; Christensen-Dalsgaard et al.
2009, and references therein), the very good agreement
between the SSM and the helioseismological constraints, mainly the
sound speed profile, the extension
of the convective envelope and the surface helium abundance, achieved
at the end of the last century has been compromised by the new
determinations of the metal abundances based on 3D photospheric models
by Asplund et al. (2005),
and only slightly alleviated by the very recent release by Asplund et al. (2009).
With these caveats, the initial helium and metal abundance of the Sun
provided
by the current SSMs allow determination of the
![]() ,
once a
primordial helium abundance
,
once a
primordial helium abundance ![]() is chosen. Table 3
shows the results of
SSMs computed by different groups by assuming different solar heavy
elements mixtures. As can be easily seen, different authors provide
values in good mutual agreement, values that translate in
is chosen. Table 3
shows the results of
SSMs computed by different groups by assuming different solar heavy
elements mixtures. As can be easily seen, different authors provide
values in good mutual agreement, values that translate in
![]() ,
if
,
if ![]() by Izotov et al. (2007)
is used.
by Izotov et al. (2007)
is used.
Table 3:
Initial helium ![]() and metal
and metal ![]() abundances provided by recent standard solar models by different
authors (see footnotes).
abundances provided by recent standard solar models by different
authors (see footnotes).
In principle the
![]() ratio can also be theoretically predicted by models of galactic
chemical evolution.
These predictions rely on several assumption on the initial mass
function, star formation rate, star formation efficiency, stellar
yields from intermediate and massive stars, ISM mixing; so
even though they are quite powerful, due to the uncertainties on each
of the aforementioned quantities they are still quite uncertain in
predicting the expected helium to metals enrichment ratio and provide
values which span a range of
ratio can also be theoretically predicted by models of galactic
chemical evolution.
These predictions rely on several assumption on the initial mass
function, star formation rate, star formation efficiency, stellar
yields from intermediate and massive stars, ISM mixing; so
even though they are quite powerful, due to the uncertainties on each
of the aforementioned quantities they are still quite uncertain in
predicting the expected helium to metals enrichment ratio and provide
values which span a range of
![]() between about 1 and 4 (Carigi
2000; Fields
& Olive 1998; Tosi 1996; Serrano & Peimbert 1981;
Timmes
et al. 1995; Chiappini et al. 1997;
Romano
et al. 2005; Carigi & Peimbert 2008; Chiappini
et al. 2002). Among the parameters that mostly
affect the outcomes of chemical evolution models we mention some of the
most important, such as the SN Ia rate, which strongly affects the iron
enrichment, the star formation history and the initial mass function,
since stars of different mass, which evolve on different time scales,
contribute differently to the production of Y and Z;
the maximum stellar mass that enriches the interstellar medium is an
other important parameter. Moreover, as far as the chemical enrichment
of the interstellar medium is concerned, stellar models, which provide
the yields to
chemical models, are still significantly affected by poorly understood
physical processes, such as convection, which affects the stellar
yields through the efficiency of dredge-up phenomena and hot-bottom
burning, mass-loss, which directly influence the enrichment, and
rotation, which has a strong impact on the helium, carbon, nitrogen and
oxygen yields (Meynet & Maeder
2002). As a consequence, stellar yields provided by different
authors still show not negligible discrepancies. Thus, the results of
chemical evolution models depend on the adopted set of stellar yields (Carigi 2000;
Fields
& Olive 1998; Chiappini et al. 2003).
For example, it has long been known that the
between about 1 and 4 (Carigi
2000; Fields
& Olive 1998; Tosi 1996; Serrano & Peimbert 1981;
Timmes
et al. 1995; Chiappini et al. 1997;
Romano
et al. 2005; Carigi & Peimbert 2008; Chiappini
et al. 2002). Among the parameters that mostly
affect the outcomes of chemical evolution models we mention some of the
most important, such as the SN Ia rate, which strongly affects the iron
enrichment, the star formation history and the initial mass function,
since stars of different mass, which evolve on different time scales,
contribute differently to the production of Y and Z;
the maximum stellar mass that enriches the interstellar medium is an
other important parameter. Moreover, as far as the chemical enrichment
of the interstellar medium is concerned, stellar models, which provide
the yields to
chemical models, are still significantly affected by poorly understood
physical processes, such as convection, which affects the stellar
yields through the efficiency of dredge-up phenomena and hot-bottom
burning, mass-loss, which directly influence the enrichment, and
rotation, which has a strong impact on the helium, carbon, nitrogen and
oxygen yields (Meynet & Maeder
2002). As a consequence, stellar yields provided by different
authors still show not negligible discrepancies. Thus, the results of
chemical evolution models depend on the adopted set of stellar yields (Carigi 2000;
Fields
& Olive 1998; Chiappini et al. 2003).
For example, it has long been known that the
![]() ratio grows by increasing the mass-loss rate of both intermediate and
massive stars (see e.g. Iben
& Truran 1978; Peimbert 1986; Renzini
& Voli 1981).
ratio grows by increasing the mass-loss rate of both intermediate and
massive stars (see e.g. Iben
& Truran 1978; Peimbert 1986; Renzini
& Voli 1981).
Chiappini et al.
(2003) predicted a value of the enrichment ratio
![]() ,
if the stellar models by Meynet
& Maeder (2002), which take into account rotation,
are adopted in their chemical evolution model, whereas a value
of 1.5 is obtained, if the stellar computations by van den Hoek & Groenewegen
(1997), for the low and intermediate mass stars, and Woosley & Weaver (1995),
for the massive ones, are used. The recent version of the chemical
evolution model by Carigi &
Peimbert (2008) provides
,
if the stellar models by Meynet
& Maeder (2002), which take into account rotation,
are adopted in their chemical evolution model, whereas a value
of 1.5 is obtained, if the stellar computations by van den Hoek & Groenewegen
(1997), for the low and intermediate mass stars, and Woosley & Weaver (1995),
for the massive ones, are used. The recent version of the chemical
evolution model by Carigi &
Peimbert (2008) provides
![]() 1.70
and 1.62, if high or low wind yields are adopted, respectively.
1.70
and 1.62, if high or low wind yields are adopted, respectively.
10 Conclusions
The principal aim of this work was to test the reliability of the
determination of ![]() by the comparison between low-MS stars and theoretical ZAMS models. A
very fine grid of stellar models has been computed for many values of
by the comparison between low-MS stars and theoretical ZAMS models. A
very fine grid of stellar models has been computed for many values of
![]() ,
[Fe/H] and masses adopting two different mixing-length parameters
,
[Fe/H] and masses adopting two different mixing-length parameters ![]() ,
namely 1.97 (our solar calibration) and 2.4, and two different sets of
atmosphere models to transform luminosities and effective temperatures
into magnitudes and color indices, the
PHOENIX GAIA v2.6.1 models (Brott
et al. 2005) and the ATLAS9 ones (Castelli & Kurucz 2003),
respectively.
,
namely 1.97 (our solar calibration) and 2.4, and two different sets of
atmosphere models to transform luminosities and effective temperatures
into magnitudes and color indices, the
PHOENIX GAIA v2.6.1 models (Brott
et al. 2005) and the ATLAS9 ones (Castelli & Kurucz 2003),
respectively.
A detailed analysis of the capabilities of the method and of the main uncertainty sources affecting the derived results has been performed by means of many numerical experiments on synthetic data set produced under controlled conditions and with precisely known properties.
One of the main findings of the paper is that the inferred
value of ![]() is quite sensitive to the age of the stellar sample, even in the case
in which only very faint (i.e. MV
> 6 mag) MS stars are selected. By means of numerical
experiment we showed that the lack of an age estimate of low mass field
stars leads to an underestimate of the inferred
is quite sensitive to the age of the stellar sample, even in the case
in which only very faint (i.e. MV
> 6 mag) MS stars are selected. By means of numerical
experiment we showed that the lack of an age estimate of low mass field
stars leads to an underestimate of the inferred
![]() of about 2 units. As a consequence, the face value of the
helium-to-metals enrichment ratio
provided by the recovery procedure applied to the solar neighborhood
stellar sample must be corrected for this age-bias.
of about 2 units. As a consequence, the face value of the
helium-to-metals enrichment ratio
provided by the recovery procedure applied to the solar neighborhood
stellar sample must be corrected for this age-bias.
Adopting our reference set of models (i.e. those with our
``solar'' calibrated ![]() )
transformed into the observational plane using the PHOENIX
GAIA v2.6.1 model atmospheres, we found
)
transformed into the observational plane using the PHOENIX
GAIA v2.6.1 model atmospheres, we found
![]() .
.
Such a result has been checked against an independent and very
accurate data set, that is, the low-MS of the Hyades cluster. This
sample has the additional advantage to be unaffected by the age-bias,
since its very young age (i.e.
![]() Myr)
guarantees that the low-mass (<
Myr)
guarantees that the low-mass (<
![]() )
MS stars which constitutes the sample are essentially unevolved. The
recovery method provided again
)
MS stars which constitutes the sample are essentially unevolved. The
recovery method provided again
![]() ,
in
perfect agreement with the result for field stars.
,
in
perfect agreement with the result for field stars.
To further check the consistency of this final result, we
calculated isochrones with
![]() (the closest in our grid of models) and the measured [Fe/H] of Hyades.
The good agreement between these isochrones and the Hyades MS, not only
in the faint part belonging to the sample but also at higher
luminosities, is a further proof of the internal consistency of the
recovery procedure.
(the closest in our grid of models) and the measured [Fe/H] of Hyades.
The good agreement between these isochrones and the Hyades MS, not only
in the faint part belonging to the sample but also at higher
luminosities, is a further proof of the internal consistency of the
recovery procedure.
The effect of a change in the assumed efficiency of the
superadiabatic convection (i.e. the ![]() parameter) in the
stellar models used to build the ZAMS and in the adopted atmosphere
models used to transform luminosities and effectives temperatures into
magnitudes and color indices has been discussed, too. More in detail,
the recovery method yield a nominal value
of
parameter) in the
stellar models used to build the ZAMS and in the adopted atmosphere
models used to transform luminosities and effectives temperatures into
magnitudes and color indices has been discussed, too. More in detail,
the recovery method yield a nominal value
of ![]() when adopting the set of theoretical models computed
with
when adopting the set of theoretical models computed
with ![]() and transformed into the observational plane by means of
PHOENIX atmosphere models and
and transformed into the observational plane by means of
PHOENIX atmosphere models and
![]() when adopting our standard set
of models with
when adopting our standard set
of models with ![]() but the ATLAS9 atmosphere models.
These values become about 3.6 and 2.5, respectively, once corrected for
the
age bias.
but the ATLAS9 atmosphere models.
These values become about 3.6 and 2.5, respectively, once corrected for
the
age bias.
Our data have [Fe/H] determinations coming from two different
sources, i.e. Nordström
et al. (2004) and Taylor
(2005) catalogs.
The 4 stars we have in common from the two catalogs show a
disagreement in the [Fe/H] scale between the two catalogs. This
disagreement was already identified in Taylor
(2005) where the author provides a Table to put the different
determinations of the two catalogs on the same [Fe/H] scale.
Nevertheless, even after the re-zeroing procedure suggested by Taylor (2005), we still find some
disagreement in the final results on
![]() when the two catalogs are considered separately. Probably an even more
accurate study of the zero points of metallicity determinations is
needed.
when the two catalogs are considered separately. Probably an even more
accurate study of the zero points of metallicity determinations is
needed.
We are very grateful to Emanuele Tognelli for his contribution to the updating of the code and to Steven N. Shore for the many pleasant discussions about the topic. P.G.P.M. thanks Wolfgang Brandner for the kind hospitality at Max-Planck-Institute for Astronomy, Heidelberg, where a part of the paper has been written. This work has been supported by PRIN-MIUR 2007 (Multiple stellar populations in globular clusters: census, characterizations and origin, PI G. Piotto)
References
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. F. N. Bash, & T. J. Barnes, ASP Conf. Ser., 336, 25 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Serenelli, A. M., & Basu, S. 2005a, ApJ, 621, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Basu, Pinsonneault, M. S., & Serenelli, A. M. 2005b, ApJ, 618, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Balser, D. S. 2006, AJ, 132, 2326 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., & Antia, H. M. 2008, Phys. Rep., 457, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Zs.f.Ap., 46, 108 [Google Scholar]
- Bessell, M. S., Castelli, F., & Plez, B. 1999, A&A, 333, 231 [Google Scholar]
- Brott, I., & Hauschildt, P. H. 2005, ESA Special Publication, 576, 565 [Google Scholar]
- Carigi, L. 2000, Rev. Mex. Astron. Astrofis., 36, 171 [NASA ADS] [Google Scholar]
- Carigi, L., & Peimbert, M. 2008, Rev. Mex. Astron. Astrofis., 44, 341 [NASA ADS] [Google Scholar]
- Casagrande, L., Flynn, C., Portinari, L., Girardi, L., & Jimenez, R. 2007, MNRAS, 382, 1516 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, V., Degl'Innocenti, S., & Marconi, M. 1999, A&A, 349, 834 [NASA ADS] [Google Scholar]
- Castellani, V., Degl'Innocenti, S., & Prada Moroni, P. G. 2001, MNRAS, 320, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, V., Degl'Innocenti, S., Prada Moroni, P. G., & Tordiglione, V. 2002, MNRAS, 334, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L., IAU Symp., 210, 20 [Google Scholar]
- Chiappini, C., & Maciel, W. J. 1994, A&A, 288, 921 [NASA ADS] [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Renda, A., & Matteucci, F. 2002, A&A, 395, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Matteucci, F., Meynet, G. 2003, A&A, 410, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chieffi, A., & Straniero, O. 1989, ApJS, 71, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., di Mauro, M. P., Houdek, G., & Pijpers, F. 2009, A&A, 494, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Churchwell, E., Mezger, P. G., & Huchtmeier, W. 1974, A&A, 32, 283 [NASA ADS] [Google Scholar]
- Deharveng, L., Pena, M., Caplan, J., & Costero, R. 2000, MNRAS, 311, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Degl'Innocenti, S., Prada Moroni, P. G., & Ricci, B. 2006, Ap&SS, 305, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Degl'Innocenti, S., Prada Moroni, P. G., Marconi, M., & Ruoppo, A. 2008, Ap&SS, 316, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Dodorico, S., Peimbert, M., & Sabbadin, F. 1976, A&A, 47, 341 [NASA ADS] [Google Scholar]
- Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] [Google Scholar]
- The Hipparcos and Tycho Catalogues (ESA 1997) [Google Scholar]
- Esteban, C., Peimbert, M., Torres-Peimbert, S., Garcia-Rojas, J. 1999, Rev. Mex. Astron. Astrofis., 35, 65 [Google Scholar]
- Faulkner, J. 1967, ApJ, 147, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Fields, B. D., & Olive, K. A. 1998, ApJ, 506, 177 [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandes, J., Lebreton, Y., & Baglin, A. 1996, A&A, 311, 127 [NASA ADS] [Google Scholar]
- Fukugita, M., & Kawasaki, M. 2006, ApJ, 646, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, Origin and Evolution of the Elements, 15 [Google Scholar]
- Guzik, J. A., Watson, L. S., & Cox, A. N. 2005, ApJ, 627, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Iben, I., Jr., & Truran, J. W. 1978, ApJ, 220, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., & Thuan, T. X. 2004, ApJ, 602, 200 [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Lipovetsky, V. A. 1994, ApJ, 435, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Lipovetsky, V. A. 1997, ApJS, 108, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Stasinska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenez, R., Flynn, C., MacDonald, J., & Gibson, B. K. 2003, Science, 299, 1552 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krishna Swamy, K. S. 1966, ApJ, 145, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D. 1986, PASP, 98, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D., & Sargent, W. L. W. 1983, ApJ, 273, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 [NASA ADS] [Google Scholar]
- Maciel, W. J. 2001, Ap&SS, 277, 545 [Google Scholar]
- Madsen, S., Dravins, D., & Lindegren, L. 2002, A&A, 381, 446 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathews, G. J., Boyd, R. N., & Fuller, G. M. 1993, ApJ, 403, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., & Wood, K. 2005, MNRAS, 360, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2002, A&A, 390, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montalban, J., D'Antona, F., Kupka, F., & Heiter, U. 2004, A&A, 416, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordtröm, B., Mayor, M., Andersen, J., et al 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olive, K. A., & Steigman, G. 1995, ApJS, 97, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Olive, K. A., Steigman, G., & Skillman, E. D. 1997, ApJ, 483, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J., & Portinari, L. 1998, MNRAS, 298, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J., Terlevich, R. J., & Melnick, J. 1986, PASP, 98, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J., Simonson, E. A., Terlevich, R. J., & Edmunds, M. G. 1992, MNRAS, 255, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1966, ApJ, 146, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M. 1986, PASP, 98, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., & Serrano, A. 1980, Rev. Mex. Astron. Astrofis., 5, 9 [NASA ADS] [Google Scholar]
- Peimbert, M., & Torres-Peimbert, S. 1974, ApJ, 193, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., & Torres-Peimbert, S. 1976, ApJ, 203, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., Peimbert, A., & Ruiz, M. T. 2000, ApJ, 541, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., Carigi, L., & Peimbert, A. 2001, Ap&SS Suppl., 277, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, A., Peimbert, M., & Luridiana, V. 2002, ApJ, 565, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., Luridiana, V., Peimbert, A., & Carigi, L. 2007, ASP Conf. Ser., 374, 81 [NASA ADS] [Google Scholar]
- Perrin, M.-N., de Strobel, G. C., Cayrel, R., & Hejlesen, P. M. 1977, A&A, 54, 779 [NASA ADS] [Google Scholar]
- Perryman, M. A. C., Brown, A. G. A., Lebreton, Y., et al. 1998, A&A, 331, 81 [NASA ADS] [Google Scholar]
- Potekhin, A. Y. 1999, A&A, 351, 787 [NASA ADS] [Google Scholar]
- Renzini, A. 1994, A&A, 285, L5 [NASA ADS] [Google Scholar]
- Renzini, A., & Voli, M. 1981, A&A, 94, 175 [NASA ADS] [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Chiappini, C., Matteucci, F., & Tosi, M. 2005, A&A, 430, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Serenelli, A. M., Basu, S., Ferguson, J. W., & Asplund, M. 2009, ApJ, 705, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Serrano, A., & Peimbert, M. 1981, Rev. Mex. Astron. Astrofis., 5, 109 [NASA ADS] [Google Scholar]
- Shternin, P. S., & Yakovlev, D. G. 2006, PhRvD, 74, 3004 [NASA ADS] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, B. J., ApJS, 161, 444 [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995, ApJS, 98, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Tognelli, E., Prada Moroni, P. G., & Degl'Innocenti, S. 2010, A&A, submitted [Google Scholar]
- Tosi, M. 1996, ASP Conf. Ser., 98, 299 [NASA ADS] [Google Scholar]
- Valle, G., Marconi, M., Degl'Innocenti, S., & Prada Moroni, P. G. 2009, A&A, 507, 1541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...
![[*]](/icons/foot_motif.png)
- Member of the International Max Planck Research School for Astronomy and Cosmic Physics at the University of Heidelberg, IMPRS-HD, Germany.
- ... (EOS)
![[*]](/icons/foot_motif.png)
- http://www-phys.llnl.gov/Research/OPAL/EOS_2005
- ... tables
![[*]](/icons/foot_motif.png)
- http://www-phys.llnl.gov/Research/OPAL/opal.html
- ... temperatures
![[*]](/icons/foot_motif.png)
- http://webs.wichita.edu/physics/opacity
- ... colors
![[*]](/icons/foot_motif.png)
- A single star becomes hotter and more luminous after leaving the ZAMS, here we are referring to the overall shape of the isochrones and ZAMS in this range of magnitudes and colors.
All Tables
Table 1: [Fe/H] for the 4 stars in common in the Taylor (2005) and Geneva-Copenhagen catalogs.
Table 2:
Y and Z values for the three
different adopted mixtures (see text in Sect. 5.5),
for two reference values of [Fe/H] and
![]() .
.
Table 3:
Initial helium ![]() and metal
and metal ![]() abundances provided by recent standard solar models by different
authors (see footnotes).
abundances provided by recent standard solar models by different
authors (see footnotes).
All Figures

|
Figure 1:
The data color-magnitude diagram. Overplotted are three ZAMS all
computed with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{14227f02.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14227-10/Timg52.png)
|
Figure 2:
Illustrative example of how theoretichal and observational
differences are computed and used to produce a
|
| Open with DEXTER | |
| In the text | |

|
Figure 3:
Results of 105 simulation runs to determine the
best fitting |
| Open with DEXTER | |
| In the text | |

|
Figure 4: Results of a test for a sample of 110 simulated stars lying on the ZAMS (see text for more details). Overplotted is the best-fit Gaussian. |
| Open with DEXTER | |
| In the text | |

|
Figure 5:
Results of a test for a sample of 110 simulated stars not lying on the
ZAMS. Ages are uniformly distributed between 0 and 7 Gyr. The solid
line gives the result when heavy elements diffusion is taken into
account, while the dashed line corresponds to the case where [Fe/H]t
is equal to [Fe/H]
|
| Open with DEXTER | |
| In the text | |

|
Figure 6:
The evolution of stars mimics lower values of the enrichment ratio. A
7 Gyr isochrone calculated for
|
| Open with DEXTER | |
| In the text | |

|
Figure 7:
Effect of changing the mixing length parameter from
|
| Open with DEXTER | |
| In the text | |

|
Figure 8:
Results for the same data set of Fig.4.
In this case we ran our Monte Carlo method using ZAMS calculated with a
mixing length parameter |
| Open with DEXTER | |
| In the text | |

|
Figure 9:
ZAMS transformed into the observational plane using PHOENIX (solid
lines) and ATLAS9 (dashed lines) model atmospheres. All the ZAMS shown
have been calculated with
|
| Open with DEXTER | |
| In the text | |

|
Figure 10:
ZAMS calculated for the three different mixtures, GN93, AGS05 and
AGSS09, with |
| Open with DEXTER | |
| In the text | |

|
Figure 11: Results of our Monte Carlo method when applied separately to the subsets of objects with [Fe/H] from T05 and N04 (the latter corrected using Table 10 of T05). The solid lines are for T05, the dashed for N04. Overplotted are the best-fit Gaussians. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm]{14227f12.eps}
\end{figure}](/articles/aa/full_html/2010/10/aa14227-10/Timg95.png)
|
Figure 12:
Output values of the recovery method when data are binned in
metallicity (see text for details). The green dashed lines represent
the |
| Open with DEXTER | |
| In the text | |

|
Figure 13: The CMD for the Hyades Main Sequence. Isochrones for two values of the age are overplotted: 500 Myr (black lines) and 600 Myr (red lines). Dashed and solid lines correspond to two different values of the chemical composition. Y and Z values are obtained from Equations (1) and (2) using [Fe/H] = 0.09 dex (dashed lines) and [Fe/H] = 0.19 dex (solid lines). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



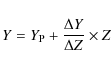
![\begin{displaymath}
Z = \frac{1-Y_{\rm P}}{1+\frac{\Delta Y}{\Delta Z}+ \frac{1}{(Z/X)_{\hbox{$\odot$ }}} \times 10^{-{\rm [Fe/H]}}} \cdot
\end{displaymath}](/articles/aa/full_html/2010/10/aa14227-10/img31.png)
![\begin{displaymath}
\mathcal{D}_j = \sum_i \left[\frac{\Delta M_{V,i} - \Delta M_{V,j}({\rm [Fe/H]}_i)}{\sigma (\Delta M_{V,i})}\right]^2 ,
\end{displaymath}](/articles/aa/full_html/2010/10/aa14227-10/img55.png)