| Issue |
A&A
Volume 521, October 2010
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200913431 | |
| Published online | 18 October 2010 | |
Non-spherical core collapse supernovae
III. Evolution towards homology and dependence on the numerical resolution
A. Gawryszczak1 - J. Guzman2 - T. Plewa2 - K. Kifonidis3
1 - Nicolaus Copernicus Astronomical Center,
Bartycka 18,
00-716 Warsaw, Poland
2 -
Department of Scientific Computing,
Florida State University,
Tallahassee, FL 32306, USA
3 -
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Straße 1,
85741 Garching, Germany
Received 8 October 2009 / Accepted 24 June 2010
Abstract
Aims. We study the hydrodynamic evolution of a non-spherical
core-collapse supernova in two spatial dimensions. We begin our study
from the moment of shock revival - taking into account neutrino heating
and cooling, nucleosynthesis, convection, and the standing accretion
shock (SASI) instability of the supernova blast - and continue for the
first week after the explosion when the expanding flow becomes
homologous and the ejecta enter the early supernova remnant (SNR)
phase. We observe the growth and interaction of Richtmyer-Meshkov,
Rayleigh-Taylor, and Kelvin-Helmholtz instabilities resulting in an
extensive mixing of the heavy elements throughout the ejecta. We obtain
a series of models at progressively higher resolution and provide a
discussion of numerical convergence.
Methods. Different from previous studies, our computations are
performed in a single domain. Periodic mesh mapping is avoided. This is
made possible by employing cylindrical coordinates, and an adaptive
mesh refinement (AMR) strategy in which the computational workload
(defined as the product of the total number of computational cells and
the length of the time step) is monitored and, if necessary, reduced.
Results. Our results are in overall good agreement with the AMR
simulations we have reported in the past. We show, however, that
numerical convergence is difficult to achieve, due to the strongly
non-linear nature of the problem. Even more importantly, we find that
our model displays a strong tendency to expand laterally away from the
equatorial plane and toward the poles. We demonstrate that this
expansion is a physical property of the low-mode, SASI
instability. Although the SASI operates only within about the first
second of the explosion, it leaves behind a large lateral velocity
gradient in the post shock layer which affects the evolution for
minutes and hours later. This results in a prolate deformation of the
ejecta and a fast advection of the highest-velocity
![]() -rich
material from moderate latitudes to the polar regions of our grid
within only 300 s after core bounce. This effect - if confirmed by
3D simulations - might actually be responsible for the global asymmetry
of the nickel lines in SN 1987A. Yet, it also poses difficulties
for the analysis of 2D SASI-dominated explosions in terms of the
maximum nickel velocities, since discretization errors at the poles are
considered non-negligible.
-rich
material from moderate latitudes to the polar regions of our grid
within only 300 s after core bounce. This effect - if confirmed by
3D simulations - might actually be responsible for the global asymmetry
of the nickel lines in SN 1987A. Yet, it also poses difficulties
for the analysis of 2D SASI-dominated explosions in terms of the
maximum nickel velocities, since discretization errors at the poles are
considered non-negligible.
Conclusions. The simulations demonstrate that significant radial
and lateral motions in the post-shock region, produced by convective
overturn and the SASI during the early explosion phase, contribute to
the evolution for minutes and hours after shock revival. They lead to
both later clump formation, and a significant prolate deformation of
the ejecta which are observed even as late as one week after the
explosion. This ejecta deformation may be considered final, since the
expansion has long become homologous by that time. As pointed out in
the recent analysis by Kjaer et al., such an ejecta morphology is in
good agreement with the observational data of SN 1987A. Systematic
future studies are needed to investigate how the SASI-induced late-time
lateral expansion that we find in this work depends on the dominant
mode of the SASI when the early explosion phase ends, and to which
extent it is affected by the dimensionality of the simulations. The
impact on and importance of the SASI for the distribution of iron group
nuclei and the morphology of the young SNR argues for future
three-dimensional explosion and post-explosion studies on
singularity-free grids that cover the entire sphere. Given the results
of our 2D resolution study, present three-dimensional simulations must
be regarded as underresolved, and their conclusions must be verified by
a proper numerical convergence analysis in three dimensions.
Key words: hydrodynamics - instabilities - shock waves - supernovae: general
1 Introduction
More than twenty years after the appearance of SN 1987A, the landmark event in both modern observational and theoretical supernova (SN) science, the growing observational SN database continues to challenge supernova modelers. It is currently accepted that core-collapse supernovae and their remnants are generally characterized by large-scale anisotropies, mixing and smaller-scale clumping of material, together with the penetration of such clumps into the outermost layers of the ejecta (see e.g. Wang & Wheeler 2008; Leonard et al. 2006; Aschenbach et al. 1995; Hughes et al. 2000; Hanuschik et al. 1988; Li et al. 1993; Kjaer et al. 2010; Wang et al. 2002, and references therein).
The general interpretation of these properties of stellar explosions is that they are the result of hydrodynamic instabilities. Stimulated mainly by SN 1987A, many research groups have performed simulations of the late-time (beyond about 1 s after core bounce) hydrodynamic evolution of core-collapse SNe in the hope to reproduce and understand these observations (for a detailed bibliography of early work along these lines see the first paper of the present series, Kifonidis et al. 2003).
Historically, such simulations can be classified into two main
types. Models in which a separate multidimensional neutrino
radiation-hydrodynamic modeling of the supernova explosion mechanism
is attempted, from which the subsequent late-time hydrodynamic
evolution is started, belong to the ``radiation-hydrodynamic explosion
initiation'' or, in short, the RHD approach. In contrast, models in
which the detailed physics of the ``supernova engine'' is neglected,
and the explosion is artificially triggered by some form of manual
energy deposition into a stellar progenitor model![]() , may be assigned to the
``non-radiation-hydrodynamic explosion initiation'' or (in short) the
non-RHD approach.
, may be assigned to the
``non-radiation-hydrodynamic explosion initiation'' or (in short) the
non-RHD approach.
The non-RHD approach is the older of the two, and has been in exclusive use - in many variations - until the late nineties. It continues to be used even today in works where the complicated physics that causes the SN explosion cannot be modeled due to computational or other constraints, and where the ease in setting up a simulation is of primary importance, as e.g. in performing first studies of three-dimensional phenomena (Hungerford et al. 2005,2003), in setting up several different explosions in a number of progenitors (Joggerst et al. 2009), or in the testing of certain hypotheses, such as the possible formation of jets during the explosion and their impact on late-time SN evolution (Couch et al. 2009).
Unfortunately, the non-RHD approach is unsatisfactory from a theoretical point of view as it neglects physics which is known to be important in the supernova context, as e.g. neutrino heating and cooling, and non-radial hydrodynamic instabilities like the standing accretion shock instability (or SASI, Foglizzo 2009; Scheck et al. 2004; Blondin et al. 2003; Laming 2007; Scheck et al. 2008), and multidimensional convection (Foglizzo et al. 2006; Scheck et al. 2008), which occur within the first second after core bounce.
This has motivated work on the more advanced models of the RHD type, which hold the promise to yield a fully consistent hydrodynamic description of the explosion, once the present computational difficulties which are connected to neutrino-driven supernova modeling (cf. Buras et al. 2006a,b) have been overcome. Such RHD models were introduced (in two spatial dimensions) by Kifonidis et al. (2000) and improved and extended in the first two installments of the present series (Kifonidis et al. 2006,2003, henceforth Papers I and II, respectively).
At present, both the RHD and the non-RHD approach make use of parametrizations and assumptions. The level of the employed approximations is, however, fundamentally different. In the non-RHD approach the entire hydrodynamic structure of a model is prescribed. A severe consequence of such ``structural parametrization'', as we will call it in the following, is the tendency to bias the subsequent evolution with preconceived notions and assumptions, which are unavoidably introduced in attempts to set up simple initial data (see the discussion in Papers I and II). In contrast, the approximations used in RHD type models mainly center on the level of accuracy at which the (computationally very expensive) neutrino physics is treated. The hydrodynamics is then calculated consistently in response to the resulting neutrino heating. The approximations made in RHD type models are therefore far less intrusive than those in models of the non-RHD type.
In Paper I, for instance, a neutrino-hydrodynamics code which was based on a simple neutrino light-bulb scheme was used to model the evolution encompassing the first second of the supernova, given a boundary condition for the dense, contracting, and neutrino-radiating neutron star core, which was excised from the computational domain for reasons of efficiency.
Paper II improved upon this treatment, by replacing the neutrino light bulb with the more accurate, gray neutrino transport scheme developed by Scheck et al. (2006). Furthermore, the boundary neutrino fluxes were taken to mimic results of supernova simulations employing full Boltzmann neutrino transport, but were slightly varied around those values. This led to a more accurate description of the ratio of hydrodynamic to heating time scales in the post-shock flow than in the models of Paper I, and allowed to properly account for large-scale, non-radial, low-mode (bi- and quadrupolar) hydrodynamic SASI instabilities during the first second of the explosion.
In both Papers I and II the late-time hydrodynamics was subsequently computed with an Adaptive Mesh Refinement (AMR) code. Followed to about six hours after core bounce, the RHD models presented in Paper II have demonstrated great potential to give good agreement with observations. One particular simulation, model b23a, was successful in accounting for the most intriguing features of SN 1987A. Based on a recent analysis of SN 1987A's ejecta morphology Kjaer et al. (2010) in fact argue that only SASI-dominated explosions (such as model b23a) are fully consistent with the observational data, while jet-induced explosions, as favored by Wang et al. (2002), are not.
Of course, the additional physics in such RHD models does not come without cost. Temporal and spatial scales need to be resolved that are absent in models of the non-RHD type. The computational problems encountered in trying to account for this physics, along with the need to evolve the models to times sufficiently late for making comparisons against observations makes such detailed modeling daunting, already in two, but even more so in three dimensions.
This is exemplified by the difficulties that Hammer et al. (2009) have experienced in attempting first three-dimensional simulations of this type. Their runs were initialized from 3D neutrino radiation-hydrodynamic simulations of the explosion performed by Scheck (2007), which served as data for late-time 3D (purely) hydrodynamic calculations. Because of limited computational resources, the 3D neutrino radiation-hydrodynamic models of Scheck (2007) had only followed four nuclear species, and lacked a detailed treatment of nucleosynthesis under non-NSE conditions. Even with this approximation, his best resolved run could only be evolved to a time of 0.5 s after bounce, just about half the evolutionary time deemed necessary in 2D modeling attempts of the explosion phase. The explosion energy in his model was therefore far from being saturated. In addition, Scheck (2007) had considered boundary neutrino fluxes that would have only given a very low-energy explosion.
In order to still use this model as initial data for their
subsequent simulations, Hammer et al. (2009) artificially changed its
energy distribution to match typical SN explosion
energies of ![]() 1 Bethe. Unfortunately, the bias for the later
evolution that such manipulation introduces is hard to
quantify. Such modification of an RHD model might, in fact, be viewed
as a regression to structural parametrization. Moreover, the
resolution that Hammer et al. (2009) could afford in three dimensions
using a single-mesh PPM code was naturally substantially inferior to
that which has been achieved in the best-resolved two dimensional
studies that made use of AMR techniques. Nevertheless, their results
are interesting, since they indicate that 2D axisymmetric
simulations overestimate the drag coefficient of newly formed clumps
which are enriched in heavy elements, an effect which has been
predicted for some time (see e.g. Paper I; and Kane et al. 2000).
While more accurate and better resolved 3D studies must and will be
performed in the future, there are still a lot of unsettled issues
even in two spatial dimensions.
1 Bethe. Unfortunately, the bias for the later
evolution that such manipulation introduces is hard to
quantify. Such modification of an RHD model might, in fact, be viewed
as a regression to structural parametrization. Moreover, the
resolution that Hammer et al. (2009) could afford in three dimensions
using a single-mesh PPM code was naturally substantially inferior to
that which has been achieved in the best-resolved two dimensional
studies that made use of AMR techniques. Nevertheless, their results
are interesting, since they indicate that 2D axisymmetric
simulations overestimate the drag coefficient of newly formed clumps
which are enriched in heavy elements, an effect which has been
predicted for some time (see e.g. Paper I; and Kane et al. 2000).
While more accurate and better resolved 3D studies must and will be
performed in the future, there are still a lot of unsettled issues
even in two spatial dimensions.
First, few calculations were carried into the phase of homology, and in the cases where this has been done (Herant & Benz 1991, 1992, Herant & Woosley 1994) the late-time models do not include the early explosion stages in a self-consistent way. Second, most of the existing models have relatively low resolution and none of the more recent works known to us has discussed numerical model convergence, or provided any estimates of accuracy for such important quantities as the maximum nickel velocities in the ejecta. As we will show in this paper even highly resolved 2D AMR models still show variations in the maximum nickel velocities. Third, in models of the RHD type the effects on these velocities due to radioactive heating by the decay of nickel and cobalt remain to date unquantified (in models that were started from simple non-RHD explosions, Herant & Benz 1992, have noticed a mild acceleration due to radioactive heating). Fourth, parameter studies with different stellar models, to investigate the sensitivity of the results on the density and pressure profiles of the progenitor, have not yet been performed for models of the RHD type. And fifth, the effects of fall-back have not been studied in most simulations, since gravity has either been completely neglected or treated in the monopole approximation.
In the present paper we are going to address the first two of these points. Our goal is to attain homologous expansion in high-resolution mesh-based simulations that are initiated from radiation-hydrodynamic models of the early SN explosion phase, and to provide a resolution study in order to quantify numerical uncertainties. Ultimately, we would like to evolve the simulations well into the SN remnant phase, in order to compare such explosion models - and hence SN theory - with a larger observational data base than it has been possible in the past. In the process we face some new challenges that such late-time computations pose. In particular we aim to resolve, with limited computational power, and within a reasonable amount of time, all crucial physics participating in the evolution.
Our models are based on the
![]() blue supergiant star by
Woosley et al. (1988). Within this progenitor is embedded the
SASI-dominated explosion model b23a that was presented in Paper II. To
allow for computations beyond the shock breakout from the stellar
surface, we have added a stellar wind outside the progenitor star. We
begin our simulations at the final time of the explosion model (
blue supergiant star by
Woosley et al. (1988). Within this progenitor is embedded the
SASI-dominated explosion model b23a that was presented in Paper II. To
allow for computations beyond the shock breakout from the stellar
surface, we have added a stellar wind outside the progenitor star. We
begin our simulations at the final time of the explosion model (![]() 1 s
after core bounce), and continue to a final simulation time of
7 days, when the expansion is expected to be completely
homologous.
1 s
after core bounce), and continue to a final simulation time of
7 days, when the expansion is expected to be completely
homologous.
We have structured this paper as follows. In Sect. 2 we shall give an overview of our computational approach, and our initial and boundary conditions. The results of our simulations will be presented in Sect. 3, starting with a discussion of the dynamics of spherically symmetric (1-D) models - which serve as a reference - and progressing to a high-resolution two-dimensional model. In Sect. 4 we provide a detailed analysis of our multidimensional simulations, commenting on aspects such as the global lateral expansion of our SASI-dominated models, the resulting anisotropy of the final metal distribution in the ejecta, the extent of the mixing of heavy elements in mass, the evolution towards homology, and the numerical convergence in two dimensions. Section 5 finally provides a summary of our findings.
2 Computational model
2.1 Hydrodynamics
We are numerically solving Euler's equations of compressible hydrodynamics in conservative form. We use the Eulerian version of the Piecewise Parabolic Method (PPM) by Colella & Woodward (1984) as implemented in A RDENT/FLASH, a parallel, block-structured, AMR hydrodynamic code (Fryxell et al. 2000). PPM is a high-order shock-capturing Godunov-type scheme (Godunov 1959), is formally second order accurate in space, and uses Strang-type directional splitting for time advancement (Strang 1968) to achieve second order accuracy in time. We are keeping track of 19 passively advected nuclear species by solving a separate advection equation for each specie. A list of the species is given in Table 1.
Table 1: Passively advected nuclear species.
The system of hydrodynamic equations is closed using an electron-positron
equation of state based on table interpolation of the Helmholtz free
energy (Timmes & Swesty 2000). The Helmholtz equation of state (EoS) takes
into account contributions from electrons and positrons (degenerate
and/or relativistic), radiation pressure, and ions assuming complete
ionization. The physical limits of this EoS are
![]() g cm-3, and
104 < T < 1011 K, appropriate for
stellar interiors and the early stages of post-explosion supernova
remnant evolution. To allow for the evolution at very late times, we have
extended the original Helmholtz EoS to the low-density, low-temperature
regime, by blending it smoothly with an ideal gas equation of state.
g cm-3, and
104 < T < 1011 K, appropriate for
stellar interiors and the early stages of post-explosion supernova
remnant evolution. To allow for the evolution at very late times, we have
extended the original Helmholtz EoS to the low-density, low-temperature
regime, by blending it smoothly with an ideal gas equation of state.
2.2 Simulation setup
Previous simulations of multidimensional core-collapse supernovae have been typically performed in spherical coordinates, which severely limits the time step due to the small grid spacing towards the center, combined with the extreme flow conditions prevailing in that region. Another drawback of using spherical geometry is the fact that while one may be resolving the interior of the star very well, the resolution is quickly lost (especially in the angular direction) at large radii. Thus the resolution is also highly nonuniform, making convergence analysis difficult. Also, while spherical geometry might be optimal at early times of the simulation, it is not desirable at later times when the dynamics we are most interested in is taking place far away from the center. Yet another disadvantage of using spherical geometry is the presence of a grid singularity at the center of the grid, which in most cases is avoided by using a computational domain whose inner radial boundary is located at a finite radius. We avoid most problems associated with a spherical mesh by using a cylindrical grid. Also, a cylindrical mesh can be easily combined with adaptive mesh refinement, avoiding cumbersome remeshing/restart procedures, and allowing us to take the simulations farther in time than we otherwise would have been able to.
Our two-dimensional cylindrical grid covers the region
![]() cm in radius and
cm in radius and
![]() cm in the vertical direction. We impose a reflecting boundary
condition at R=0 (symmetry axis) and allow for free flow everywhere
else. The center of the star, where the neutron star is forming, is
approximated by a non-moving gravitating sink hole. The hole is
treated as a point-mass located at the grid center with an initial
mass of
cm in the vertical direction. We impose a reflecting boundary
condition at R=0 (symmetry axis) and allow for free flow everywhere
else. The center of the star, where the neutron star is forming, is
approximated by a non-moving gravitating sink hole. The hole is
treated as a point-mass located at the grid center with an initial
mass of
![]() .
It occupies a semi-circular region extending up
to 3 computational cells from the center. The velocity of the material
inside the hole is reset to zero after every step. The density inside
the sink hole is kept constant (
.
It occupies a semi-circular region extending up
to 3 computational cells from the center. The velocity of the material
inside the hole is reset to zero after every step. The density inside
the sink hole is kept constant (
![]() of the density of
the material just outside the hole) and the mass of material accreted
into the hole is added to the central point mass (representing the
neutron star). The gravity of the central mass and the self-gravity of
the mass residing on the grid are calculated in the spherically
symmetric (monopole) approximation.
of the density of
the material just outside the hole) and the mass of material accreted
into the hole is added to the central point mass (representing the
neutron star). The gravity of the central mass and the self-gravity of
the mass residing on the grid are calculated in the spherically
symmetric (monopole) approximation.
At the start of our simulation the grid is populated with three
distinct components. Excluding the inner core occupied by the sink
hole, the explosion component extends up to a radius of
![]() cm. (In what follows, the radial distance from the
grid origin is denoted as r.) The explosion component is the b23a model at a time of t=0.92 s after core bounce, that was obtained in
Paper II. Model b23a in turn is based on the WPE15 ls (180)
post-collapse model of the
cm. (In what follows, the radial distance from the
grid origin is denoted as r.) The explosion component is the b23a model at a time of t=0.92 s after core bounce, that was obtained in
Paper II. Model b23a in turn is based on the WPE15 ls (180)
post-collapse model of the
![]() progenitor of Woosley et al. (1988)
presented by Bruenn (1993).
progenitor of Woosley et al. (1988)
presented by Bruenn (1993).
In an attempt to minimize a possible contribution and
accumulation of numerical discretization errors near the polar axis
of the explosion model, two 10-degree wide sections near the axis of
model b23a were overwritten by mirror-reflections of the abutting
mesh regions (i.e. in these regions the density, for instance, was
initialized according to
![]() ).
However, pronounced axial flows still developed during the
subsequent evolution. As we will show below, these axial flows are
promoted by the global lateral expansion of that SASI explosion
model. We recognize that the flow dynamics near the symmetry axis
is due to a blend of a real physical effect, the fact that the
degrees of freedom of the flow are restricted, and the likely
presence of non-negligible discretization errors in these regions (see
Sect. 4).
).
However, pronounced axial flows still developed during the
subsequent evolution. As we will show below, these axial flows are
promoted by the global lateral expansion of that SASI explosion
model. We recognize that the flow dynamics near the symmetry axis
is due to a blend of a real physical effect, the fact that the
degrees of freedom of the flow are restricted, and the likely
presence of non-negligible discretization errors in these regions (see
Sect. 4).
The progenitor model is identical to that which we already used in
Paper II (Woosley, private communication). The model envelope
extends up to a radius of
![]() cm. The
remaining portion of the computational domain is filled with a stellar wind. The wind is spherically symmetric with a velocity of
15
cm. The
remaining portion of the computational domain is filled with a stellar wind. The wind is spherically symmetric with a velocity of
15
![]() ,
a temperature of
,
a temperature of
![]() K, and a density
corresponding to a constant mass loss rate of
K, and a density
corresponding to a constant mass loss rate of
![]() yr-1. To map the explosion and progenitor
component to our computational domain we employ monotonic cubic
interpolation (Steffen 1990).
yr-1. To map the explosion and progenitor
component to our computational domain we employ monotonic cubic
interpolation (Steffen 1990).
2.3 Computational strategy
Since A RDENT/FLASH uses AMR we are able to study the hydrodynamic evolution with many levels of refinement. In our case the mesh is refined if there are density jumps >0.2, pressure jumps >0.4, or if the abundance of nickel exceeds 10% by mass. We initially start the simulations with a large number of refinement levels and then remove these levels depending on the instantaneous number of zones (to limit memory use), and the calculated step size (to limit computational time). The latter two refinement criteria allow us to control the total computational cost of an individual model.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13431fg1.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg69.png)
|
Figure 1:
Computational workload in the two-dimensional 15 km
resolution model of a supernova explosion as a function of the
logarithm of the simulation time. The number of zones is shown
with a thick solid line ( bottom curve). The simulation begins
with an effective resolution of 15 km which is gradually
decreased with time; at the final time the effective model
resolution is 393 216 km. The wall-clock time per double
time-step is shown with a thin line ( upper curve). Rapid
variations in the wall-clock time are partly due to mesh refinement
( |
| Open with DEXTER | |
In Fig. 1 we show the number of mesh cells (bottom curve) as a function of the
simulation time. The top curve in this figure shows the wall-clock
time for every double time-step in the simulation. We note 4-5 s variations (![]() 15% amplitude) in the wall-clock time
due to mesh adaptation, which takes place every other double time
step. Erratic variations of much larger (
15% amplitude) in the wall-clock time
due to mesh adaptation, which takes place every other double time
step. Erratic variations of much larger (![]() 20-30 s) amplitude
correspond to writing output files (extreme cases are due to
I/O congestion on the computing system).
20-30 s) amplitude
correspond to writing output files (extreme cases are due to
I/O congestion on the computing system).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13431fg2.epsi}\hspace*{3mm}
\includegraphics[width=7.5cm,clip]{13431fg3.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg71.png)
|
Figure 2:
Supernova shock dynamics in one- and two-dimensional
explosion models. ( Left panel) Evolution of the shock speed
(left scale) as a function of radius in the one-dimensional
(thin) and two-dimensional (medium line) 15 km model. The run of
the mass distribution
|
| Open with DEXTER | |
The general semi-periodic shape of the curves reflects our refinement
strategy. During each cycle occupying several hundred time steps, the
number of computational cells increases. Once the maximum allowed
number of cells is reached, the finest level of refinement is
automatically removed and the computation proceeds without
interruption. The mesh level removal is done gradually over several
time steps to avoid problems with mapping the mesh hierarchy to the
process space. Occasionally, the flow conditions may change such that
the time step is reduced below a certain threshold (e.g. during shock
acceleration at
![]() ,
see also
Fig. 2
below) and significantly many more mesh cells are removed to limit the
computational workload. The total computational cost of the 15 km
model is
,
see also
Fig. 2
below) and significantly many more mesh cells are removed to limit the
computational workload. The total computational cost of the 15 km
model is
![]() steps and
steps and
![]() h on
NERSC's Franklin Cray XT4 with 32 cores.
h on
NERSC's Franklin Cray XT4 with 32 cores.
3 Model results
Although the main focus of this work is the effects of two-dimensional hydrodynamic instabilities, we start with one-dimensional models as these are useful for understanding the gross overall dynamics of the system, serve as a reference point in the development of two-dimensional models, and - very importantly in the present context - help optimizing computational strategies in adaptive simulations. In two spatial dimensions fluid instabilities typically grow at contact discontinuities due to the preexisting flow perturbations and the interaction with the passing shock wave. This complicates the flow pattern, and usually renders the models too costly for making numerous adjustments to the simulation strategy.
We expect that our simulations will be largely consistent with those reported in Paper II. This is because several essential components of the two models, both physics-related and computational, are common. However, we anticipate to observe also some differences due to the highly non-linear nature of the problem, the use of a different grid geometry, the lack of mesh remapping, and the overall higher mesh resolution.
3.1 Spherically symmetric model
We have computed one-dimensional models at effective resolutions of
240, 120, 60, 30, and 15 km. Figure 3
shows the density distribution as a function of the logarithm of the
radius in these one-dimensional models at t=7 days. As we increase
the effective resolution from 240 km (dashed line in
Fig. 3) to 120 km (dotted line), the density
increases by ![]() 25% at the first density maximum (
25% at the first density maximum (
![]() )
and decreases by
)
and decreases by ![]() 10% at the second maximum
(
10% at the second maximum
(
![]() ). Doubling the resolution to 60 km (thin
solid line) results in a mild density increase at both maxima by
<10%. The density at the second maximum oscillates with the
resolution with a progressively smaller amplitude, while more
monotonic convergence is observed at the first maximum. Despite the
aforementioned variations, the one-dimensional density profile seems
fairly well established already at a resolution of 60 km.
). Doubling the resolution to 60 km (thin
solid line) results in a mild density increase at both maxima by
<10%. The density at the second maximum oscillates with the
resolution with a progressively smaller amplitude, while more
monotonic convergence is observed at the first maximum. Despite the
aforementioned variations, the one-dimensional density profile seems
fairly well established already at a resolution of 60 km.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{13431fg4.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg76.png)
|
Figure 3: Density profiles in log scale as a function of the logarithm of the radius in the densest part of the ejecta in one-dimensional models at the final time (t=7 days). Results are shown for models with a resolution of 15 (thick solid), 30 (medium solid), 60 (thin solid), 120 (dotted), and 240 km (dashed line). Note the gradual decrease in the density variation as the mesh resolution increases, which is indicative of numerical convergence. The density profiles of models with a resolution of at least 60 km appear very closely matched. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13431fg5.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg77.png)
|
Figure 4: Evolution of the density in log scale before shock breakout for the one-dimensional explosion model at an effective resolution of 15 km. The initial positions of the Si/O, (C+O)/He, and He/H composition interfaces are marked by dotted vertical lines. |
| Open with DEXTER | |
We begin our simulation at t=0.92 s after core bounce with the
supernova shock located just past the Si/O interface at
![]() cm (see Fig. 4).
Behind the supernova shock one can notice a reverse shock at
cm (see Fig. 4).
Behind the supernova shock one can notice a reverse shock at
![]() cm that was formed when the main shock entered
the oxygen core (cf. Paper I). In between the two shocks sits a
dense shell of metal-rich material which contains most of the ejecta
mass. The dense shell is moving outward due in part to its momentum,
and the combined action of pressure gradients in the shocked gas, the
gravity of the central mass, and the self-gravity of the
progenitor. The reverse shock present at t=0.92 s eventually
disappears from the grid as it passes through the inner region (sink
hole), but is partially reflected. In addition to the original reverse
shock, two more reverse shocks form during the passage of the
supernova shock through the envelope. The first of those
reverse shocks originates when the supernova shock enters the
helium shell, and the second one after the shock enters the
hydrogen envelope. Those shocks can be seen in
Fig. 4 at t=20 s and t=1500 s at radius
cm that was formed when the main shock entered
the oxygen core (cf. Paper I). In between the two shocks sits a
dense shell of metal-rich material which contains most of the ejecta
mass. The dense shell is moving outward due in part to its momentum,
and the combined action of pressure gradients in the shocked gas, the
gravity of the central mass, and the self-gravity of the
progenitor. The reverse shock present at t=0.92 s eventually
disappears from the grid as it passes through the inner region (sink
hole), but is partially reflected. In addition to the original reverse
shock, two more reverse shocks form during the passage of the
supernova shock through the envelope. The first of those
reverse shocks originates when the supernova shock enters the
helium shell, and the second one after the shock enters the
hydrogen envelope. Those shocks can be seen in
Fig. 4 at t=20 s and t=1500 s at radius
![]() cm and
cm and
![]() cm,
respectively. They form when the leading shock first
accelerates and then decelerates, which means the freshly shocked
material is moving slower than the shocked material at earlier
time. This leads to piling up of the shocked material, and local
density and pressure increase. If the conditions are right, and the
shocked material moves supersonically with respect to the dense
region, this acoustic perturbation becomes a reverse shock
(Herant et al. 1994). Similarly to the original reverse shock, the
additional reverse shocks are reflected off the central region.
cm,
respectively. They form when the leading shock first
accelerates and then decelerates, which means the freshly shocked
material is moving slower than the shocked material at earlier
time. This leads to piling up of the shocked material, and local
density and pressure increase. If the conditions are right, and the
shocked material moves supersonically with respect to the dense
region, this acoustic perturbation becomes a reverse shock
(Herant et al. 1994). Similarly to the original reverse shock, the
additional reverse shocks are reflected off the central region.
A shock wave accelerates (decelerates) when it travels through a
medium with the density decreasing faster (slower) than
![]() (Sedov 1959; Herant et al. 1994). In other words the shock speed
depends on the mass overrun by the shock,
(Sedov 1959; Herant et al. 1994). In other words the shock speed
depends on the mass overrun by the shock,
![]() .
Due to the density structure of the progenitor, the supernova
shock propagates through the star in an unsteady fashion. It is the
unsteady propagation of the supernova shock that is responsible for
Rayleigh-Taylor instabilities that develop along material interfaces
(Chevalier & Klein 1978; Herant et al. 1994). The propagation of the blast through
the star is illustrated in Fig. 2. While moving
through the C+O core, the shock initially accelerates to slightly over
20 000
.
Due to the density structure of the progenitor, the supernova
shock propagates through the star in an unsteady fashion. It is the
unsteady propagation of the supernova shock that is responsible for
Rayleigh-Taylor instabilities that develop along material interfaces
(Chevalier & Klein 1978; Herant et al. 1994). The propagation of the blast through
the star is illustrated in Fig. 2. While moving
through the C+O core, the shock initially accelerates to slightly over
20 000
![]() .
Then it slows down in its motion through the helium
shell to
.
Then it slows down in its motion through the helium
shell to
![]()
![]() .
Upon entering the hydrogen envelope,
it briefly speeds up, and subsequently decelerates again, to
.
Upon entering the hydrogen envelope,
it briefly speeds up, and subsequently decelerates again, to
![]()
![]() .
Around
.
Around
![]() (
(
![]() s) the shock
begins to accelerate in the outer stellar layers, ultimately reaching
velocities of
s) the shock
begins to accelerate in the outer stellar layers, ultimately reaching
velocities of
![]()
![]() .
Once the blast has left the
envelope, it gradually slows down inside the stellar wind. This last
acceleration/deceleration sequence gives rise to the formation of a
final reverse shock, and is responsible for the growth of a
Rayleigh-Taylor instability at the interface between the shocked
ejecta and the shocked wind (see below). The shock is traveling at
.
Once the blast has left the
envelope, it gradually slows down inside the stellar wind. This last
acceleration/deceleration sequence gives rise to the formation of a
final reverse shock, and is responsible for the growth of a
Rayleigh-Taylor instability at the interface between the shocked
ejecta and the shocked wind (see below). The shock is traveling at
![]()
![]() when it leaves the computational domain at
when it leaves the computational domain at
![]() days.
days.
3.2 Two-dimensional model
Although one-dimensional models provide invaluable information about several major characteristics of the exploding star, qualitatively new phenomena emerge in multidimensions. These are chiefly related to fluid flow instabilities developing at the material interfaces that separate various nuclear species. In what follows, our intention is to highlight the richness and complexity of the mixing process rather than to provide a quantitative comparison of contributions of the individual participating hydrodynamic instabilities. We feel the value of such a quantitative comparison would be extremely limited and could possibly produce confusion given the long list of uncertainties involved in the physical model (progenitor) or numerics (mesh resolution, assumed symmetry). We therefore think it is justified to offer solely a qualitative discussion.
The main process leading to mixing of different elements in supernovae is the Rayleigh-Taylor instability (RTI, Sadot et al. 2005; Sharp 1984; Youngs 1984; Chandrasekhar 1961). The RTI requires the presence of a material interface separating fluids at two different densities and a sustained acceleration pointing across the interface from lighter to denser material. This situation naturally arises in thermonuclear supernovae, where hot and light ashes of nuclear fuel buoyantly expand into unburned material (Khokhlov 1995; Müller & Arnett 1986; Nomoto et al. 1976). In core-collapse supernovae, however, the acceleration at the material interfaces is due to a positive pressure gradient that results from the acceleration and deceleration phases of the supernova shock's motion. As we discussed in the previous section, the supernova shock experiences two major deceleration episodes during its propagation inside the envelope, and one more deceleration phase after it leaves the star and sweeps through the wind (see right panel in Fig. 2). Each deceleration phase creates a positive pressure gradient in layers with a negative density gradient, i.e. conditions suitable for RTI.
Besides the RTI, two more fluid instabilities are at work in our case. The Richtmyer-Meshkov instability (RMI, Brouillettee 2002; Meshkov 1969; Richtmyer 1960) occurs at material interfaces subjected to an impulsive acceleration that (in the core-collapse supernova setting) is provided by the supernova shock and also a series of reverse shocks sweeping through the ejecta. Although the overall radial expansion clearly dominates the explosion dynamics, initial flow nonuniformities and later contributions from the RTI and RMI produce velocity shear, naturally inducing the Kelvin-Helmholtz instability (KHI, Youngs & Williams 2008; Chandrasekhar 1961; Sohn & Hwang 2005; Lamb 1932). Both the RTI and RMI, as well as the KHI, grow from small-scale features in the current problem and thus their role can be quantified only in well-resolved models. To our knowledge, no such quantitative comparison of contributions of various instabilities has ever been done. It is also beyond the scope of the present study.
In our two-dimensional models we can only observe the combined action
of all three instabilities. An assessment of the relative
contributions of the RMI and the RTI based solely on the flow
morphology is an extremely daunting task. At the end of the linear
phase, both instabilities produce very similar structures differing
only in details (see e.g. Abarzhi et al. 2003). We may expect, however, that different
instabilities will dominate the evolution at various times.
The RMI will contribute only after a sufficiently aspherical shock
interacts with a (radial) density gradient. The RTI contribution will
be non-vanishing only in zones with pressure and density gradients of
opposite signs. If such conditions can be sustained for a sufficiently
long time, the RTI with its asymptotic t2 growth will (locally)
outpace the RMI contribution (which scales as
![]() ). Yet,
the present simulations - and the RTI growth rates presented in
Paper I - indicate that this is not universally the case.
In particular at the He/H interface of our progenitor model,
RMI-growth dominates.
This can be understood by considering that the initial growth time
scales are,
). Yet,
the present simulations - and the RTI growth rates presented in
Paper I - indicate that this is not universally the case.
In particular at the He/H interface of our progenitor model,
RMI-growth dominates.
This can be understood by considering that the initial growth time
scales are,
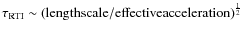 ,
and
,
and
![]() .
The velocity difference (postshock vs.
unshocked envelope) is by far greater than the (effective rate of)
deceleration at the H/He interface. Also, small scale perturbations
grow faster in the RMI than in the RTI. This latter factor is further
amplified by the RMI which initially decreases the amplitude of the
preexisting perturbations in case of He/H (heavy/light) interfaces
(see Brouillettee 2002, Sect. 3.1). Both factors result in the RMI
dominating over the RTI, at least initially.
It can also be expected that due to the relatively weak shear along
the interfaces, the KHI growth will be modest, will occur at late
times, and have less impact than either the RTI or RMI on the
evolution.
.
The velocity difference (postshock vs.
unshocked envelope) is by far greater than the (effective rate of)
deceleration at the H/He interface. Also, small scale perturbations
grow faster in the RMI than in the RTI. This latter factor is further
amplified by the RMI which initially decreases the amplitude of the
preexisting perturbations in case of He/H (heavy/light) interfaces
(see Brouillettee 2002, Sect. 3.1). Both factors result in the RMI
dominating over the RTI, at least initially.
It can also be expected that due to the relatively weak shear along
the interfaces, the KHI growth will be modest, will occur at late
times, and have less impact than either the RTI or RMI on the
evolution.
![\begin{figure}
\par\includegraphics[width=8cm,height=3.7cm,clip]{13431fg6.eps}\p...
...eps}\par\includegraphics[width=8cm,height=3.7cm,clip]{13431fg8.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg94.png)
|
Figure 5: Density distribution in log scale in the 15 km resolution model. ( top) t=4 s; ( middle) t=20 s; ( bottom) t=300 s. Note the presence of two post-SASI bubbles, wrapped in dense metal-rich material, and several triple points (kinks) along the forward shock front at early times; the dense shell features well-developed RTI decorations at t=20 s. |
| Open with DEXTER | |
In our subsequent discussion of the evolution in multidimensions we
will focus on the best resolved model obtained at a resolution of
15 km. We will defer commenting on numerical convergence to
Sect. 4.6 below. Figure 5 shows the density distribution at selected times during the first 5 min after core bounce. At t=4 s (top panel in
Fig. 5), the central region around
(z,R)=(0,0) cm is occupied by the sink hole representing the nascent
neutron star. The material located right outside the hole and in the
equatorial plane is falling back onto the neutron star. The supernova
shock is highly deformed with two low-density bubbles occupying most
of the core region, a clear reminiscence of the low-mode SASI
instability in the b23a model (see also Fig. 3c of Paper II). The
shock front shows several kinks (triple points), the most pronounced
are visible at
![]() ,
,
![]() ,
and
,
and
![]() cm. As time progresses, those triple points move along the
shock surface, and are sites of strong vorticity deposition at the
material interfaces, significantly enhancing mixing.
cm. As time progresses, those triple points move along the
shock surface, and are sites of strong vorticity deposition at the
material interfaces, significantly enhancing mixing.
At t=20 s (Fig. 5, middle panel) the
supernova shock has already traversed through the (C+O)/He interface
and Rayleigh-Taylor instabilities are now fully developed in the dense
shell of material bounded by the supernova shock and the resultant
reverse shock. The kinks in the supernova shock front are clearly
visible although their positions are now slightly different. We notice
clear signs of the Kelvin-Helmholtz instability developing at the
contact surface associated with the leftmost triple point near
![]() .
Two large streams of matter
form a Y-shaped feature along the equator and feed the neutron
star. The edges of both streams show pronounced KHI decorations.
.
Two large streams of matter
form a Y-shaped feature along the equator and feed the neutron
star. The edges of both streams show pronounced KHI decorations.
During the following few hundred seconds, the supernova shock becomes
progressively less aspherical while the dense central region undergoes
dramatic morphological changes. By t=300 s
(Fig. 5, bottom panel), the supernova shock
has just passed the He/H interface and sweeps through the hydrogen
envelope. The slowing shock causes the formation of a ``helium wall''
behind it. Two pronounced ``scars'' are visible at the wall at
![]() and at
and at
![]() .
These flow features are imprints left by
the passing triple points. They will play a crucial role in the deep
mixing of the outer layers into the central regions with large amounts
of hydrogen already penetrating into the helium shell.
.
These flow features are imprints left by
the passing triple points. They will play a crucial role in the deep
mixing of the outer layers into the central regions with large amounts
of hydrogen already penetrating into the helium shell.
At this time we also see that the Rayleigh-Taylor instabilities have grown substantially. In two regions, highly decorated RTI ``fingers'' have managed to pass through the layers which are in the process of forming the reverse shock at the inner surface of the helium wall. The third finger-like feature is located closer to the equatorial plane and extends half way through the low density core region. The Y-shaped accretion feature, clearly noticeably at earlier times, can now be barely recognized as it becomes more extended laterally and suffers from flow instabilities.
The dense material that penetrates into the layers of the forming helium wall is of particular interest, as it is composed of fast-moving, metal-rich clumps. Heavy elements are also dominant in the jet-like polar outflows visible near R=0 and penetrating all the way up to the supernova shock. The origin of these features is discussed in Sect. 4.1.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg9.eps}\hspace*{1mm}...
...eps}\hspace*{1mm}
\includegraphics[width=7.6cm,clip]{13431fg12.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg101.png)
|
Figure 6:
Density distribution in log scale in the 15 km resolution
model. (Top left) t=1500 s; ( top right) t=5000 s; (bottom left) t=10 000 s; (bottom right) t=1 day. The polar outflows
are clearly visible at t=5000 s, affecting model
morphology for angles
|
| Open with DEXTER | |
The supernova structure between t=1500 s and t=1 d is shown in
Fig. 6. It can be described as a composite of the supernova shock and its
post-shock region, the mixing layer populated with a network of dense,
metal-rich structures and inward-penetrating hydrogen-rich bubbles,
and the central, low density ejecta being swept by the reverse shock
formed at the base of the helium wall. At t=1500 s (top-left panel
in Fig. 6), the reverse shock is fully formed and
is about to overrun the middle RTI feature. Hydrogen bubbles are now
more clearly visible, especially the one in the upper left section of
the ejecta. Most of the fast moving metal-rich material is trapped
inside the helium wall although some material
![]() appears successful in
penetrating all the way into the hydrogen envelope.
appears successful in
penetrating all the way into the hydrogen envelope.
By t=5000 s (top-right panel in Fig. 6) the
supernova shock is accelerating in its motion through the outer parts
of the stellar envelope. It breaks through the stellar surface at
![]() s. Substantially more metal-rich clumps are now moving
through the hydrogen envelope and both hydrogen bubbles are fully
developed. There are signs of a mild RTI developing at the outer
surface of the helium wall, best visible close to the equator. The
reverse shock is sweeping through the low density core overrunning the
network of the RTI-fragmented, metal-rich shell in the process. The
central part of the ejecta undergoes relatively little changes
later. Most metal-rich features visible at t=5000 s can be clearly
identified also at t=10 000 s, and t=1 day (bottom-left and
bottom-right panel in Fig. 6, respectively). The only
major change is due to the passage of the reverse shock through the
central region of the ejecta. This event does not affect the overall
structure of the core, however.
s. Substantially more metal-rich clumps are now moving
through the hydrogen envelope and both hydrogen bubbles are fully
developed. There are signs of a mild RTI developing at the outer
surface of the helium wall, best visible close to the equator. The
reverse shock is sweeping through the low density core overrunning the
network of the RTI-fragmented, metal-rich shell in the process. The
central part of the ejecta undergoes relatively little changes
later. Most metal-rich features visible at t=5000 s can be clearly
identified also at t=10 000 s, and t=1 day (bottom-left and
bottom-right panel in Fig. 6, respectively). The only
major change is due to the passage of the reverse shock through the
central region of the ejecta. This event does not affect the overall
structure of the core, however.
Although at these late times the ejecta morphology appears well-established, it is the outer regions of the young supernova remnant where a significant RTI finally comes into play. This is due to the final deceleration of the supernova shock inside the stellar wind: the less dense shocked wind material is now moving slower than the shocked and denser outer stellar layers. The interface separating the shocked stellar envelope from the shocked stellar wind is RTI-unstable (see Nymark et al. 2006; Chevalier et al. 1992, and references therein) and numerous RTI fingers are formed in the process (Fig. 7).
| Figure 7:
Density distribution in log scale in the 15 km
resolution model at t=10 000 s including the supernova
shock. Note the Rayleigh-Taylor instability developing at the
interface between the shocked stellar ejecta and the shocked
wind at a distance
|
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13431fg14.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg105.png)
|
Figure 8:
Angle-averaged structure of the 15 km model at t=12 h. Shown is the density (thick solid), pressure (medium
solid), radial velocity (thin solid), hydrogen mass fraction
(thin dotted), nickel mass fraction (thick dotted), and ratio of
internal to total energy (thin solid). The RTI-unstable
interface between the shocked ejecta and the shocked stellar
wind is located around
|
| Open with DEXTER | |
Figure 8 shows the angle-averaged radial structure of the young supernova
remnant at t=12 h. The outermost RTI-mixing region is clearly
visible in the density, velocity and pressure profiles for
![]() cm. Note that at this time
the metal-rich core occupies only
cm. Note that at this time
the metal-rich core occupies only ![]() 10% of the innermost
region (
10% of the innermost
region (
![]() cm). The ejecta are now approaching
homologous expansion as indicated by the low ratio of the internal to
the total energy. The only exception is the freshly shocked
RTI-unstable outermost region. The relatively large internal energy
content of the core (
cm). The ejecta are now approaching
homologous expansion as indicated by the low ratio of the internal to
the total energy. The only exception is the freshly shocked
RTI-unstable outermost region. The relatively large internal energy
content of the core (![]() 10% at
10% at
![]() cm, and a few
percent at the core's edge) is due to the recent passage of the
reverse shock; the core continues to expand ballistically and will
quickly cool adiabatically.
cm, and a few
percent at the core's edge) is due to the recent passage of the
reverse shock; the core continues to expand ballistically and will
quickly cool adiabatically.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg15.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg109.png)
|
Figure 9:
Temporal evolution of integrated quantities in
the two-dimensional 15 km resolution model. (Thick solid)
explosion energy; (medium solid) total energy (sum of the
internal and kinetic energy); (thin solid) gravitational energy;
(thin dotted) internal energy; (medium dotted) kinetic energy;
(thick dotted) integrated |
| Open with DEXTER | |
The low overall internal energy content is confirmed in Fig. 9 in which we show the evolution of the model's energies and the
integrated vorticity up to the moment when the shock leaves the
computational domain. The internal and kinetic energy vary together in
sync, reflecting the variations in the shock speed (cf. Fig. 2). They are both
![]() erg as
long as the shock remains inside the star. The internal energy rapidly
decreases after the shock breakout through the stellar photosphere,
and amounts to
erg as
long as the shock remains inside the star. The internal energy rapidly
decreases after the shock breakout through the stellar photosphere,
and amounts to ![]() 1.5% of the total energy at
1.5% of the total energy at
![]() h, when the shock leaves the grid. It is interesting to note the
large variations of the vorticity during the shock breakout. These
variations are due to the rapid increase in the shock speed and slight
global asphericity of the shock front. The vorticity evolution prior
to shock breakout is consistent with that of the models presented in Paper II.
A direct comparison of our
Fig. 9 with Fig. 5 of Paper II is
not possible, though, as the latter displays the evolution of the
vorticity in inner layers of the ejecta (i.e. up to the He/H
interface) for the early phase after shock breakout. In passing
we note that a realistic model of shock breakout must include
radiation effects (Calzavara & Matzner 2004, and references therein), which
are not considered in this work. We expect, however, that these
effects will not affect mixing of the metal-rich core nor the
structure of the young supernova remnant emerging within the first few
days after explosion.
h, when the shock leaves the grid. It is interesting to note the
large variations of the vorticity during the shock breakout. These
variations are due to the rapid increase in the shock speed and slight
global asphericity of the shock front. The vorticity evolution prior
to shock breakout is consistent with that of the models presented in Paper II.
A direct comparison of our
Fig. 9 with Fig. 5 of Paper II is
not possible, though, as the latter displays the evolution of the
vorticity in inner layers of the ejecta (i.e. up to the He/H
interface) for the early phase after shock breakout. In passing
we note that a realistic model of shock breakout must include
radiation effects (Calzavara & Matzner 2004, and references therein), which
are not considered in this work. We expect, however, that these
effects will not affect mixing of the metal-rich core nor the
structure of the young supernova remnant emerging within the first few
days after explosion.
| Figure 10: Density distribution in log scale in the 15 km resolution model at t=7 days. |
|
| Open with DEXTER | |
The density distribution in the model at the final time, t=7 days, is shown in Fig. 10. Except for the apparent density increase in the central region due to the reverse shock, the overall structure of the metal-rich part of the ejecta is quite similar to that obtained a few hours after the core bounce, and the major high-velocity features can be easily identified already at t=5000 s (see Fig. 6). We also note that the origins of some ejecta features, in particular those of the hydrogen-rich bubbles, can be tracked all the way back to the first few minutes after the core bounce.
The most conspicuous feature visible in Fig. 10, though, is the pronounced anisotropy of the ejecta. These have approximately the form a prolate ellipsoid with a major to minor axis ratio around 1.6. This was already pointed out in Paper II based on simulations that were evolved to a time of 20 000 s after core bounce. Figure 10 demonstrates that this result holds even for the evolution into the homologous phase. In fact, Fig. 10 might be regarded as giving an accurate picture of the ejecta morphology even beyond that phase since the ensuing expansion is expected to be self-similar, i.e. the morphology will remain frozen in the flow.
4 Discussion
4.1 The SASI-induced lateral expansion: flow dynamics
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13431fg17.epsi}\includegraphics[width=7.6cm,clip]{13431fg18.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg113.png)
|
Figure 11:
Angular structure of the 15 km resolution model. (Left panel) radial averages of density (thick solid), pressure (thin solid), radial velocity (thin dotted), and lateral
|
| Open with DEXTER | |
A very important effect that we find in the present simulations, whose consequences have not been recognized previously (although they were present in the simulations of Paper II), is the presence of a large lateral velocity gradient in our initial SASI explosion model (cf. the left panel of Fig. 11). Due to this gradient the model shows a strong lateral expansion, away from the equator and toward the poles which leads to an accumulation of material in the polar regions, within minutes to hours after core bounce (see the right panel of Fig. 11).
Figure 12 - which depicts the angular distribution of several radially-averaged quantities in the young supernova remnant at t=7 days - demonstrates that this anisotropy is preserved until the end of our simulations. Note that the density (shown with a thick solid line in Fig. 12 and in the left panel of Fig. 11) is highest inside the polar regions. Note also that the initial angular distribution of the density is essentially uniform (shown with a thin solid line in the right panel of Fig. 11).
The global lateral expansion contributes decisively to shape the ejecta into the final form visible in Fig. 10. It is also essential for the formation of the bulges of material that are visible at the poles of the exploding star as early as t=300 s into the evolution (bottom panel in Fig. 5). These axial flows are the result of a complex interaction between the strong SASI lateral expansion, and the fact that reflecting boundaries are used at the symmetry axis which restrict the degrees of freedom of the flow. Being continuously fed by the lateral motion, and encountering the impenetrable boundary at the axis, the path of least resistance for the fluid is to expand along the poles.
In the past, these axial flows have been regarded to be mainly the result of discretization errors near the axial coordinate singularity, and conical sections near the poles were used to exclude these regions from further analysis. However, the pivotal role of the SASI-induced lateral expansion, indicates that this interpretation does not account for the true contribution of the various involved effects. Without the strong continuous feeding by the global lateral flow, the axial outflows cannot become that strong. This is indicated by the fact that the SASI-dominated explosions which are considered in both the present paper and Paper II show very pronounced axial flows, while the models presented in Paper I, where the SASI was absent, showed much weaker axial features. Consistent with this observation is the fact that in the limit of a completely vanishing lateral flow, as it is for instance the case in 2D simulations of Sedov blast waves on spherical grids, such axial outflows are not present.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg19.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg114.png)
|
Figure 12:
Angular structure of the 15 km resolution model at the
final time. Radial averages are shown for the density (thick solid),
pressure (medium solid), radial velocity (thin solid), and mass
fraction of hydrogen, oxygen, and nickel (dashed, thin dotted,
and thick dotted line, respectively). Radial averages include
only data for distances
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{13431fg20.epsi}\hspace*{4.5mm}
\includegraphics[width=8.2cm,clip]{13431fg21.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg115.png)
|
Figure 13:
Distribution of nickel in the 15 km resolution
model. (Left panel) The angular distribution of the nickel mass
is shown at 0.92 s (thin dotted), 20 s (thick dotted),
300 s (thin solid), 5000 s (medium solid), and t=7 days
(thick solid). Note the fast advection of nickel to the
north pole (
|
| Open with DEXTER | |
4.2 The SASI-induced lateral expansion: heavy elements redistribution
Another very important effect of the SASI-generated lateral expansion
is that it causes a lateral redistribution of material enriched in
heavy elements. Figure 13 shows the evolution of the
angular distribution of the nickel mass in our 15 km resolution 2D
model. The initial SASI explosion model contains two nickel-rich
sectors centered around
![]() and
and
![]() (thin dotted line in the left panel of
Fig. 13). During the subsequent evolution, the
SASI-generated lateral velocity field of this model
(cf. Fig. 11) causes a steady drift of the
nickel toward the polar regions.
(thin dotted line in the left panel of
Fig. 13). During the subsequent evolution, the
SASI-generated lateral velocity field of this model
(cf. Fig. 11) causes a steady drift of the
nickel toward the polar regions.
Of the two nickel concentrations, the material initially located at
![]() is actually the fastest moving nickel-rich
material on our grid, with velocities approaching 4000
is actually the fastest moving nickel-rich
material on our grid, with velocities approaching 4000
![]() (see
the right panel of Fig. 13). This material is advected
over half a quadrant of the computational domain and to the north pole
in less than 300 s after core bounce (thin solid line in the
left panel of Fig. 13).
(see
the right panel of Fig. 13). This material is advected
over half a quadrant of the computational domain and to the north pole
in less than 300 s after core bounce (thin solid line in the
left panel of Fig. 13).
The evolution of the nickel-rich sector initially located near the
equator is somewhat more complex as it eventually distributes nickel
in a broad region between
![]() and
and
![]() .
There is a relatively well-defined nickel-rich ``clump''
(actually a torus-like structure, given that our simulations make use
of axisymmetry) at
.
There is a relatively well-defined nickel-rich ``clump''
(actually a torus-like structure, given that our simulations make use
of axisymmetry) at
![]() moving with a velocity of
moving with a velocity of
![]() 2500
2500
![]() .
.
In addition to becoming enriched with nickel, the polar regions are relatively rich in oxygen (thin dotted line in Fig. 12) but devoid of hydrogen (dashed line in Fig. 12). This lateral advection of heavy elements poses difficulties for the analysis of our 2D simulations, as it transports the nickel clumps over time into regions of the computational domain where discretization errors are expected to be non-negligible and the accuracy of the solution is largely unknown. There is significant ambiguity in what should and what shouldn't be accounted for in these regions when computing the maximum nickel velocities. Given that it is not just numerical errors which are contributing, but a true physical effect (i.e. the global lateral expansion) is involved too, it is for instance not at all clear whether the use of an exclusion cone around the symmetry axis is a justified and viable approach, or how large that exclusion cone should be made. This ambiguity is impossible to overcome in axisymmetric models. It is of a particular consequence since in our highest resolution 2D model it affects the highest velocity nickel clumps present in our 2D simulations which are of importance for explaining the data of SN 1987A.
To illustrate this further we show in Fig. 14 the
mass distribution of the nickel in velocity space for our 15 km
resolution 2D model at t=7 days, as obtained by employing exclusion
cones of different widths. The maximum nickel velocity as determined
without using any exclusion cone at all (
![]() ),
is close to 4000
),
is close to 4000
![]() .
This value decreases gradually to 3350
.
This value decreases gradually to 3350
![]() ,
3250
,
3250
![]() ,
and 3200
,
and 3200
![]() if cones with a width
if cones with a width
![]() of
of
![]() ,
,
![]() ,
and
,
and ![]() are used, respectively. The
error in determining this velocity could thus be as high as 25%,
depending on what one considers to be a true feature of the solution.
are used, respectively. The
error in determining this velocity could thus be as high as 25%,
depending on what one considers to be a true feature of the solution.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg22.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg121.png)
|
Figure 14:
Mass distribution of the nickel in radial velocity space
in the two-dimensional 15 km resolution model at t=7 days.
Data for different widths of the polar exclusion cone
|
| Open with DEXTER | |
4.3 Extent of the mixing of different elements
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13431fg23.epsi}\hspace*{3mm}
\includegraphics[width=7.5cm,clip]{13431fg24.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg122.png)
|
Figure 15:
Composition of the two-dimensional 15 km model at
t=10 000 s. ( Left panel) entire computational domain; ( right panel) |
| Open with DEXTER | |
In evaluating the extent of the mixing of different elements in mass
we again show results considering both the entire computational
domain, and a ![]() wide wedge centered around the equator
(z=0 cm) (thereby excluding a cone with width
wide wedge centered around the equator
(z=0 cm) (thereby excluding a cone with width
![]() around the symmetry axis). The latter approach is similar
to what has been done in previous work (though the conical section
used, e.g., in Paper II had an extent of only
around the symmetry axis). The latter approach is similar
to what has been done in previous work (though the conical section
used, e.g., in Paper II had an extent of only ![]() ).
).
Figure 15 compares the amount of mixing in the 15 km
model as inferred from the entire domain (left panel) to the mixing in
the region limited to the equatorial wedge (right panel). As we can
see, essentially all material mixed beyond
![]() is
associated with the polar regions of the model. Slightly increasing
the extent of the exclusion cone, i.e. making the equatorial wedge
still narrower, does not change the above picture significantly.
is
associated with the polar regions of the model. Slightly increasing
the extent of the exclusion cone, i.e. making the equatorial wedge
still narrower, does not change the above picture significantly.
Comparing the species distribution as a function of mass at
t=10 000 s (right panel in Fig. 15) with Fig. 6 of
Paper II, we observe that at this intermediate time the extent of
mixing in our present high-resolution two-dimensional simulation
matches the amount reported in Paper II very well. For example the
average position of the He/H interface given in Paper II is
![]() ,
essentially identical to that obtained in our 15 km
model. In both studies H is mixed down to
,
essentially identical to that obtained in our 15 km
model. In both studies H is mixed down to
![]() while
while
![]() is mixed out to
is mixed out to
![]() .
The agreement is thus excellent.
.
The agreement is thus excellent.
By comparing the species distribution at t=10 000 s (right panel in
Fig. 15) to that at t=7 days
(Fig. 16), we can, moreover, see that most
of the mixing takes place within the first 2 or 3 h of the
supernova explosion. This observation is consistent with the ratio of
the internal to total energy decreasing to ![]() 0.15 by
t=10 000 s (see Fig. 18 and the discussion in
Sect. 4.4). At that time, lateral pressure gradients are
very small, and the fluid elements move nearly ballistically.
0.15 by
t=10 000 s (see Fig. 18 and the discussion in
Sect. 4.4). At that time, lateral pressure gradients are
very small, and the fluid elements move nearly ballistically.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg25.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg129.png)
|
Figure 16:
Composition in the equatorial section (polar regions
excluded) of the two-dimensional 15 km resolution model at
t=7 days. Mass fractions in log scale are shown as a function
of the radial mass coordinate for hydrogen (thin solid),
|
| Open with DEXTER | |
As it has been discussed extensively in Paper II, both the inward
mixing of hydrogen and the outward mixing of nickel are crucial for an
understanding of SN 1987A's data. The inward mixing of hydrogen down
to
![]() is required for explaining the broad peak of the light
curve and the very low minimum hydrogen velocities of this supernova,
which according to Kozma & Fransson (1998) were
is required for explaining the broad peak of the light
curve and the very low minimum hydrogen velocities of this supernova,
which according to Kozma & Fransson (1998) were ![]() 700
700
![]() .
Figure 17, which displays mass distributions in
velocity space for the different nuclear species at the final
simulation time, demonstrates that this is excellently reproduced by
our models. Again an exclusion cone around the symmetry axis with
.
Figure 17, which displays mass distributions in
velocity space for the different nuclear species at the final
simulation time, demonstrates that this is excellently reproduced by
our models. Again an exclusion cone around the symmetry axis with
![]() has been used for producing this
figure. The outward mixing of nickel to a mass coordinate of
has been used for producing this
figure. The outward mixing of nickel to a mass coordinate of
![]() is tantamount to the presence of nickel-rich material on the grid with
velocities
is tantamount to the presence of nickel-rich material on the grid with
velocities ![]() 3200
3200
![]() .
We will return to this point in
Sect. 4.6, where we will discuss the dependence of
the nickel velocity distribution on the numerical resolution.
.
We will return to this point in
Sect. 4.6, where we will discuss the dependence of
the nickel velocity distribution on the numerical resolution.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg26.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg133.png)
|
Figure 17:
Mass distributions in radial velocity space in the
two-dimensional 15 km resolution model at t=7 days. The
distribution of mass is shown for hydrogen (thin solid),
|
| Open with DEXTER | |
4.4 Evolution towards homology
The evolution of the system towards homology is characterized by the
ratio of internal to total energy. As we discussed in
Sect. 3.2, the internal energy of the exploding supernova
varies during the early stages of shock propagation through the
envelope. It begins to decrease steadily for ![]() s (see
Fig. 9), when the supernova shock starts its final
acceleration phase prior to breaking out through the stellar surface.
At this time the internal energy amounts to about half of the total
energy of the supernova and exhibits substantial variations in angle
(medium solid line in Fig. 18).
s (see
Fig. 9), when the supernova shock starts its final
acceleration phase prior to breaking out through the stellar surface.
At this time the internal energy amounts to about half of the total
energy of the supernova and exhibits substantial variations in angle
(medium solid line in Fig. 18).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13431fg27.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg135.png)
|
Figure 18:
Evolution of the internal to total (internal plus
kinetic) energy ratio in the 15 km resolution model. Radial
averages of the energy ratio are shown at 0.92 s (thin solid),
1500 s (medium solid), 5000 s (thin dotted), 10 000 s
(medium dotted), 12 h (thick solid), and 7 days (thick
dotted). Radial averages include only data for distances
|
| Open with DEXTER | |
These are largely smoothed out by t=5000 s (thin dotted line in
Fig. 18). The average internal energy content drops
to ![]() 15% by t=10 000 s, and well below 5% by t=12 h. It is unclear whether this remaining energy is sufficient to
modify the expansion velocities of our 15 km model. Using a polar
exclusion cone of
15% by t=10 000 s, and well below 5% by t=12 h. It is unclear whether this remaining energy is sufficient to
modify the expansion velocities of our 15 km model. Using a polar
exclusion cone of
![]() width around the poles, we observe a
relatively modest increase of the maximum nickel velocity on the grid
by about 12%, from
width around the poles, we observe a
relatively modest increase of the maximum nickel velocity on the grid
by about 12%, from ![]() 2850
2850
![]() at t=10 000 s (not shown)
to
at t=10 000 s (not shown)
to ![]() 3200
3200
![]() at t=7 days
(Fig. 17). However, and as explained in
Sect. 4.2, at these late times the
nickel-rich material in question is located so close to the north
pole, that the determination of the maximum nickel velocity is
affected by the ambiguity in choosing the width of the exclusion cone
(see also Sect. 4.6). With the morphology of the flow
remaining essentially unchanged for t > 5000 s, it is, however, safe
to state that, for the employed blue supergiant progenitor model, the
ejecta become homologous during the first day of the evolution.
at t=7 days
(Fig. 17). However, and as explained in
Sect. 4.2, at these late times the
nickel-rich material in question is located so close to the north
pole, that the determination of the maximum nickel velocity is
affected by the ambiguity in choosing the width of the exclusion cone
(see also Sect. 4.6). With the morphology of the flow
remaining essentially unchanged for t > 5000 s, it is, however, safe
to state that, for the employed blue supergiant progenitor model, the
ejecta become homologous during the first day of the evolution.
4.5 Comparison to one-dimensional models
As a final illustration of the importance of the multidimensional effects in our models we contrast angle-averaged radial profiles obtained from our 15 km resolution two-dimensional model (left panel in Fig. 19) with plots of our corresponding spherically symmetric (1D) model with the same resolution and at the final time (right panel in Fig. 19).
Both models appear to produce explosions of comparable energies as
indicated by the radial velocity profiles. Both models are also quite
similar for radii
![]() cm, i.e. in regions
unaffected by mixing in multidimensions. However, at smaller radii, we
observe an extensive mixing of nuclear species. For example,
substantial amounts of oxygen are present at
cm, i.e. in regions
unaffected by mixing in multidimensions. However, at smaller radii, we
observe an extensive mixing of nuclear species. For example,
substantial amounts of oxygen are present at
![]() cm, and hydrogen is mixed down to
cm, and hydrogen is mixed down to
![]() cm in the multidimensional model. The density jump
associated with the H/He interface, which is clearly visible at
cm in the multidimensional model. The density jump
associated with the H/He interface, which is clearly visible at
![]() cm in 1-D, is completely smeared in
multidimensions. The only source of mixing in 1-D is numerical
diffusion, while hydrodynamic instabilities - which are partly caused
by the initial shock nonuniformity - contribute to mixing in
multidimensions.
cm in 1-D, is completely smeared in
multidimensions. The only source of mixing in 1-D is numerical
diffusion, while hydrodynamic instabilities - which are partly caused
by the initial shock nonuniformity - contribute to mixing in
multidimensions.
Note the presence of regions of opposite density and pressure
gradients, as required by the Rayleigh-Taylor instability, in the
spherically symmetric model at
![]() cm and
cm and
![]() cm. The former region is associated with
the outer edge of the nickel-rich region, while the latter is
connected to the H/He interface; both regions experienced vigorous
mixing in multidimensions, as expected.
cm. The former region is associated with
the outer edge of the nickel-rich region, while the latter is
connected to the H/He interface; both regions experienced vigorous
mixing in multidimensions, as expected.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13431fg28.epsi}\hspace*{4.5mm}
\includegraphics[width=8.05cm,clip]{13431fg29.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg141.png)
|
Figure 19:
Structure of the exploding supernova in the 15 km resolution
models at the final time of t=7 days.
( Left panel) Two-dimensional model. ( Right panel) One-dimensional model. In both panels we show the distributions of
density (thick solid), pressure (medium solid), radial velocity
(thin), hydrogen mass fraction (dashed),
|
| Open with DEXTER | |
4.6 Numerical convergence in multidimensions
Our final concern is mesh convergence (see Sect. 3.1 for a discussion of the one-dimensional case). The quantity which is of largest importance for comparison to observations and which shows the most sensitive dependence on the mesh resolution of our 2D models is the nickel distribution. In contrast, the distribution of e.g. hydrogen is very similar in all of our 2D models. We will therefore focus on the nickel distribution in what follows.
It is important to note that for the present problem proper convergence analysis is made very difficult by several effects. First, no analytic solution for the problem is known, making it impossible to determine the actual solution error. Second, the problem is highly non-linear. Thus, even if one would obtain an estimate of the instantaneous solution error by Richardson extrapolation, the contribution and interaction of higher order error terms, which are not captured by this technique, must be considered highly likely. An estimate of the instantaneous solution error is, moreover, not relevant as we are primarily interested in the accuracy of the solution at late times, when the error has accumulated. And third, in the context of the present axisymmetric simulations, significant difficulties and ambiguities for the analysis of the simulations are encountered near the poles.
In Fig. 14 we have already demonstrated that the
high-velocity tail of the nickel distribution of our 15 km resolution
model at t=7 days depends sensitively on the width of the exclusion
cone that is used around the symmetry
axis. Figure 20 shows that the same is true
in our lower-resolved 30 km and 60 km models. Particular noteworthy is
that the maximum nickel velocity as obtained from these figures
depends on both the width of the exclusion cone,
![]() ,
and
on the numerical resolution of the simulation.
,
and
on the numerical resolution of the simulation.
Table 2:
Dependence of the maximum nickel velocities (in
![]() )
in our two-dimensional models with different spatial resolution
on the width of the polar exclusion cone
)
in our two-dimensional models with different spatial resolution
on the width of the polar exclusion cone
![]() .
.
Table 2 summarizes this dependence for
convenience. It demonstrates that for no value of
![]() ,
convergence in the maximum nickel velocities is observed with
increasing resolution. In fact, the obtained maximum nickel velocities
are not even monotonic if an exclusion cone with a finite width is
used. Only for the case where no exclusion cone at all is employed
(
,
convergence in the maximum nickel velocities is observed with
increasing resolution. In fact, the obtained maximum nickel velocities
are not even monotonic if an exclusion cone with a finite width is
used. Only for the case where no exclusion cone at all is employed
(
![]() )
do we observe monotonically increasing
maximum nickel velocities with increasing resolution, which, however,
do not show a clear sign of convergence.
)
do we observe monotonically increasing
maximum nickel velocities with increasing resolution, which, however,
do not show a clear sign of convergence.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13431fg30.epsi}\hspace*{4mm}
\includegraphics[width=8.2cm,clip]{13431fg31.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg142.png)
|
Figure 20: Same as Fig. 14 but for our two-dimensional models with 30 km resolution ( left panel), and 60 km resolution ( right panel). |
| Open with DEXTER | |
From Table 2 we can only infer a lower limit for
the maximum nickel velocities at t=7 days of ![]() 3200
3200
![]() .
It
is also noteworthy that for a 240 km resolution model, Guzman (2009)
reported a qualitatively different nickel distribution, with no nickel
moving faster than
.
It
is also noteworthy that for a 240 km resolution model, Guzman (2009)
reported a qualitatively different nickel distribution, with no nickel
moving faster than ![]() 2100
2100
![]() .
In his study, significant
amounts of nickel moving with velocities >3000
.
In his study, significant
amounts of nickel moving with velocities >3000
![]() are observed
for the first time at a resolution of 120 km, which is consistent with
what we find here. The maximum velocity of Fe-group elements reported
in Paper II, where an exclusion cone of
are observed
for the first time at a resolution of 120 km, which is consistent with
what we find here. The maximum velocity of Fe-group elements reported
in Paper II, where an exclusion cone of
![]() was
used, is
was
used, is ![]() 3300
3300
![]() (see Fig. 8 of that work). This is in
good agreement with the above results, although mesh remapping, and a
different mesh geometry were used in this earlier work, and the
evolution was followed to only 20 000 s after core bounce.
(see Fig. 8 of that work). This is in
good agreement with the above results, although mesh remapping, and a
different mesh geometry were used in this earlier work, and the
evolution was followed to only 20 000 s after core bounce.
From Figs. 14 and 20 it is
furthermore obvious that also the amount of nickel in the
high-velocity tail shows no signs of convergence. Even between the
better resolved models it can differ by up to a factor of three, when
no exclusion cone is used to analyze the simulations. Using exclusion
cones of finite width, the differences become even larger. In
contrast, the mass of heavy elements moving at 1000-2400
![]() is
quite similar in the models presented here: the mass of nickel
expanding with
is
quite similar in the models presented here: the mass of nickel
expanding with ![]() 2000
2000
![]() converges to within a factor of 2-3 (the same holds in case of the 120 km model obtained by
Guzman 2009). In addition, this result is less sensitive
to the width of the exclusion cone around the symmetry axis.
converges to within a factor of 2-3 (the same holds in case of the 120 km model obtained by
Guzman 2009). In addition, this result is less sensitive
to the width of the exclusion cone around the symmetry axis.
It should be noted that in addition to the variations introduced by
the numerical resolution, and the ambiguity of analyzing the
simulations near the poles, there are two further uncertainties in the
models that concern the nickel velocities and the initial nickel
distribution. First, our axisymmetric simulations tend to overestimate
the drag coefficient of true three-dimensional clumps
(Hammer et al. 2009; Kane et al. 2000). And second, the abundance ratios of different
iron-group nuclei in neutrino-driven supernova models depend very
sensitively on the neutrino luminosities, and cannot be calculated
accurately with a grey neutrino transport scheme, as e.g. the one that
was employed in calculating model b23a (see Paper II). In other words,
the
![]() abundance in model b23a may be lower than in
reality, favoring nuclei like
abundance in model b23a may be lower than in
reality, favoring nuclei like
![]() ,
,
![]() ,
etc.,
instead. In Paper II we have tried to compensate for this uncertainty
by considering only the total mass fraction of iron group
nuclei in the analysis of velocity distributions. We have proceeded
similarly here - lumping together different iron group nuclei into
what we called the ``nickel'' abundance - since the total abundance
of the iron-group is expected to be a more reliable quantity than its
individual abundances, and can thus serve as an upper limit to the
,
etc.,
instead. In Paper II we have tried to compensate for this uncertainty
by considering only the total mass fraction of iron group
nuclei in the analysis of velocity distributions. We have proceeded
similarly here - lumping together different iron group nuclei into
what we called the ``nickel'' abundance - since the total abundance
of the iron-group is expected to be a more reliable quantity than its
individual abundances, and can thus serve as an upper limit to the
![]() abundance. A more detailed investigation of these issues
is required, though, and will be given in future work.
abundance. A more detailed investigation of these issues
is required, though, and will be given in future work.
5 Conclusions
We presented the results and detailed analysis of a series of axisymmetric hydrodynamic simulations of the first week of the evolution of a non-spherical core-collapse supernova. Different from our previous work, our computations were performed in a single domain using cylindrical coordinates. We implemented a workload-constrained mesh adaption strategy that allowed us to complete the simulations given limited computational resources, and to avoid the cumbersome periodic mesh remapping used in past studies (Couch et al. 2009; Kifonidis et al. 2006). We obtained a series of models at progressively higher mesh resolution and provided insight into the numerical convergence of our simulations.Our simulations are the first to follow a SASI-dominated explosion from shortly after its initiation into the homologous expansion and early SNR phase. Especially during the first several hours of this evolution, the ejecta are characterized by complex interactions between Rayleigh-Taylor, Richtmyer-Meshkov, and Kelvin-Helmholtz instabilities, which produce an extensive mixing and outward penetration of stellar layers enriched in heavy elements. The global asphericity of the supernova shock is, moreover, essential for triggering a deep inward penetration of hydrogen and helium into the central ejecta regions. For the particular explosion model and progenitor that we have studied, the ejecta become homologous approximately one day after the explosion.
A very important result of our present simulations is that the 2D SASI instability, which acts during the explosion launching phase, not only determines the structure of our model around that time, but leaves also a strong, large-scale imprint in the ejecta in the form of a significant lateral velocity gradient (Fig. 11), which affects the evolution for minutes to hours later (i.e. for several RT-growth time scales). This means that although the radiative driving of the explosion essentially ends around 1 s after the core bounce, it is actually incorrect to consider the late-time evolution as a phase which is completely detached from the history of the explosion.
This strong lateral expansion of SASI explosion models sheds new light onto the formation of the polar outflows which have been observed in previous axisymmetric simulations of late-time supernova evolution. It had actually been mentioned in Paper II that the appearance of these outflows was likely not due to a single numerical problem, but rather due to the combination of the restriction of the degrees of freedom of the flow, the use of reflecting boundaries at the axis of symmetry, and the presence of a coordinate singularity, and hence the possible occurrence of non-negligible discretization errors at this axis.
A crucial finding of our present work is that even this quite differentiated view for the formation of the polar outflows is incomplete. It neglects the fact that also a physical cause is involved, namely the strong late-time lateral expansion of 2D SASI explosion models. Our simulations indicate that this is actually the dominant effect for the formation of such pronounced flows near the symmetry axis. The strong lateral expansion away from the equatorial plane and toward the poles has, moreover, two very important consequences for the observational outcome of the models: it results in an inevitable advection of high-velocity nickel-rich material from moderate latitudes toward the poles, and it contributes to ultimately shape the ejecta into the form of a prolate ellipsoid.
In the present model, the highest velocity nickel on our grid, which
moves with speeds close to 4000
![]() and is consistent with the data
of SN 1987A, is advected within only 300 s after core bounce
over half a quadrant of the computational domain. In other words,
although this nickel-rich material is initially located far away from
the axis, by the end of the simulation it has ended up close to the
poles. If confirmed in future three-dimensional simulations, this
effect of the SASI might actually explain the asymmetric nickel lines
of SN 1987A.
and is consistent with the data
of SN 1987A, is advected within only 300 s after core bounce
over half a quadrant of the computational domain. In other words,
although this nickel-rich material is initially located far away from
the axis, by the end of the simulation it has ended up close to the
poles. If confirmed in future three-dimensional simulations, this
effect of the SASI might actually explain the asymmetric nickel lines
of SN 1987A.
Yet, since the accuracy of the solution is largely unknown near the poles, there is significant ambiguity in what should be accounted for in these regions when computing the maximum nickel velocities of our 2D simulations. Given that a physical effect is involved in transporting material to the poles, it is for instance not at all clear whether the use of an exclusion cone at the poles - which was customary in earlier simulations - is indeed justified. It is also unclear how large such an exclusion cone should be made. This ambiguity is impossible to overcome in axisymmetric models.
The medium (i.e. 60 km, and 30 km) resolution models and partly also the high (i.e. 15 km) resolution model that we presented here, yield results which are in very good agreement with the simulations reported in Paper II (Kifonidis et al. 2006), although these latter simulations were obtained with a different code, and a different computational strategy, and were followed to only 20 000 s after core bounce. In particular we found that the amount of mixing of both light and heavy elements, and the maximum nickel velocities in both studies agree well.
The extent of the mixing of heavy elements in our high-resolution
simulations differs qualitatively from models which are less well
resolved (as e.g. the 240 km model obtained by
Guzman 2009). At high resolutions, the mass distribution
displays a pronounced hump with velocities <1000
![]() and a long
tail extending out to
and a long
tail extending out to ![]() 3200
3200
![]() .
The hump region shows signs
of convergence while quantitative differences are seen in the tail. At
the end of the simulations, the highest nickel velocities vary between
3200
.
The hump region shows signs
of convergence while quantitative differences are seen in the tail. At
the end of the simulations, the highest nickel velocities vary between
3200
![]() and
and ![]() 4000
4000
![]() ,
while the mass of the fastest moving
nickel varies by at least a factor 2-3 between our best resolved
models. These results are sensitive as to whether the polar regions
are included in the analysis or not. This shows that due to the strong
non-linearity of the problem, and the ambiguity in analyzing
two-dimensional simulations near the axis of symmetry, strict
numerical convergence is difficult to achieve. It also implies that
present three-dimensional simulations, with their much lower
resolution, must be viewed as being far from resolved, and that their
conclusions must be verified by a proper numerical convergence
analysis in three dimensions.
,
while the mass of the fastest moving
nickel varies by at least a factor 2-3 between our best resolved
models. These results are sensitive as to whether the polar regions
are included in the analysis or not. This shows that due to the strong
non-linearity of the problem, and the ambiguity in analyzing
two-dimensional simulations near the axis of symmetry, strict
numerical convergence is difficult to achieve. It also implies that
present three-dimensional simulations, with their much lower
resolution, must be viewed as being far from resolved, and that their
conclusions must be verified by a proper numerical convergence
analysis in three dimensions.
The second important effect of the SASI-induced lateral expansion is that it contributes significantly to the strong prolate deformation of the ejecta, as it is observed at the end of our simulations (i.e. at t=7 days). This ejecta deformation may be considered final, because the expansion has long become homologous by that time. As Kjaer et al. (2010) have pointed out in their recent study, it is moreover in very good agreement with the ejecta morphology of SN 1987A, making the assumption of a ``jet-induced'' explosion unnecessary.
Given the importance of the SASI-induced late-time lateral expansion for both SNR morphology and the distribution of heavy elements, systematic future studies are required to investigate how it depends on the dominant SASI mode when the early explosion phase ends. In the present simulations it is the l=2 (quadrupolar) mode of the SASI which ultimately became dominant, but other modes are clearly possible in 2D simulations (Scheck et al. 2006), while little is known in the three-dimensional case. Since a thorough survey of SASI mode outcomes cannot be completed in two dimensions and considering furthermore the problems that the analysis of 2D simulations poses with regard to the determination of the maximum nickel velocities, 3D high-resolution simulations should be performed as soon as corresponding computational resources will allow for that. Such three-dimensional simulations will need to employ singularity-free grids that cover the entire sphere, in order to be free of the aforementioned problems, and hence of optimal use in both early and long-time supernova modeling.
AcknowledgementsWe thank Paul Drake for helpful discussions and encouragement, and an anonymous referee for his comments on the manuscript, which have helped us to improve the clarity of our presentation. A.G. was supported by the Polish Ministry of Science through the grant 92/N-ASTROSIM/2008/0. T.P. was supported through the DOE grant DE-FG52-03NA000064. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231, NASA's Astrophysics Data System, and software in part developed by the DOE-supported ASC/Alliance Center for Astrophysical Thermonuclear Flashes at the University of Chicago.
References
- Abarzhi, S. I., Nishihara, K., & Glimm, J. 2003, Phys. Lett. A, 317, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Aschenbach, B., Egger, R., & Trümper, J. 1995, Nature, 373, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Mezzacappa, A., & DeMarino, C. 2003, ApJ, 584, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Brouillettee, M. 2002, Ann. Rev. Fluid Mech., 32, 445 [Google Scholar]
- Bruenn, S. W. 1993, in Nuclear Physics in the Universe, ed. M. W. Guidry, & M. R. Strayer (Bristol: IOP), 31 [Google Scholar]
- Buras, R., Janka, H., Rampp, M., & Kifonidis, K. 2006a, A&A, 457, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buras, R., Rampp, M., Janka, H., & Kifonidis, K. 2006b, A&A, 447, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzavara, A. J., & Matzner, C. C. 2004, MNRAS, 351, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and hydromagnetic stability (Oxford: Clarendon) [Google Scholar]
- Chevalier, R. A., & Klein, R. I. 1978, ApJ, 219, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., Blondin, J. M., & Emmering, R. T. 1992, ApJ, 392, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Colella, P., & Woodward, P. R. 1984, J. Comput. Phys., 54, 174 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Couch, S. M., Wheeler, J. C., & Milosavljevic, M. 2009, ApJ, 696, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Foglizzo, T. 2009, ApJ, 694, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Foglizzo, T., Scheck, L., & Janka, H.-T. 2006, ApJ, 652, 1436 [Google Scholar]
- Fryxell, B., Olson, K., Ricker, P. M., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Godunov, S. K. 1959, Mat. Sb., 47, 271 [Google Scholar]
- Guzman, J. 2009, Msc Thesis, Florida State University [Google Scholar]
- Hammer, N. J., Janka, H., & Mueller, E. 2010, ApJ, 714, 1371 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuschik, R. W., Thimm, G., & Dachs, J. 1988, MNRAS, 234, 41P [NASA ADS] [CrossRef] [Google Scholar]
- Herant, M., & Benz, W. 1991, ApJ, 370, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Herant, M., & Benz, W. 1992, ApJ, 387, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Herant, M., & Woosley, S. E. 1994, ApJ, 425, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Herant, M., Benz, W., Hix, W. R., Fryer, C. L., & Colgate, S. A. 1994, ApJ, 435, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, J. P., Rakowski, C. E., Burrows, D. N., & Slane, P. O. 2000, ApJ, 528, L109 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hungerford, A. L., Fryer, C. L., & Warren, M. S. 2003, ApJ, 594, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Hungerford, A. L., Fryer, C. L., & Rockefeller, G. 2005, ApJ, 635, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Joggerst, C. C., Woosley, S. E., & Heger, A. 2009, ApJ, 693, 1780 [NASA ADS] [CrossRef] [Google Scholar]
- Kane, J., Arnett, D., Remington, B. A., et al. 2000, ApJ, 528, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Khokhlov, A. M. 1995, ApJ, 449, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Kifonidis, K., Plewa, T., Janka, H.-T., & Müller, E. 2000, ApJ, 531, L123 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kifonidis, K., Plewa, T., Janka, H.-T., & Müller, E. 2003, A&A, 408, 621 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kifonidis, K., Plewa, T., Scheck, L., Janka, H.-T., & Müller, E. 2006, A&A, 453, 661 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kjaer, K., Leibundgut, B., Fransson, C., Jerkstrand, A., & Spyromilio, J. 2010, A&A, 517, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kozma, C., & Fransson, C. 1998, ApJ, 497, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, H. 1932, Hydrodynamics (New York: Dover) [Google Scholar]
- Laming, J. M. 2007, ApJ, 659, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, D. C., Filippenko, A. V., Ganeshalingam, M., et al. 2006, Nature, 440, 505 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Li, H., McCray, R., & Sunyaev, R. A. 1993, ApJ, 419, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Meshkov, E. E. 1969, Fluid. Dyn., 4, 151 [Google Scholar]
- Müller, E., & Arnett, W. D. 1986, ApJ, 307, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Sugimoto, D., & Neo, S. 1976, Ap&SS, 39, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Nymark, T. K., Fransson, C., & Kozma, C. 2006, A&A, 449, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richtmyer, R. D. 1960, Commun. Pure Appl. Math., 13, 297 [CrossRef] [Google Scholar]
- Sadot, O., Smalyuk, V. A., Delettrez, J. A., et al. 2005, Phys. Rev. Lett., 95, 265001 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Scheck, L. 2007, Ph.D. Thesis, Technische Universität München [Google Scholar]
- Scheck, L., Plewa, T., Janka, H.-T., Kifonidis, K., & Müller, E. 2004, , 92, 011103 [Google Scholar]
- Scheck, L., Kifonidis, K., Janka, H.-T., & Müller, E. 2006, A&A, 457, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scheck, L., Janka, H.-T., Foglizzo, T., & Kifonidis, K. 2008, A&A, 477, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics (New York: Academic Press) [Google Scholar]
- Sharp, D. H. 1984, Physica D, 42, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Sohn, S.-I., & Hwang, W. 2005, J. Phys. Soc. Japan, 74, 1472 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, M. 1990, A&A, 239, 443 [NASA ADS] [Google Scholar]
- Strang, G. 1968, SIAM J. Numer. Anal., 5, 506 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., & Wheeler, J. C. 2008, ARA&A, 46, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Wheeler, J. C., Höflich, P., et al. 2002, ApJ, 579, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Pinto, P. A., & Ensman, L. 1988, ApJ, 324, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Youngs, D. L. 1984, Physica D, 42, 32 [Google Scholar]
- Youngs, D. L., & Williams, R. J. R. 2008, Int. J. Num. Meth. Fluids, 56, 1597 [CrossRef] [Google Scholar]
Footnotes
- ... model
![[*]](/icons/foot_motif.png)
- Usually in one spatial dimension by the employment of a piston or a thermal bomb, and sometimes in two dimensions by the use of manufactured aspherical initial shock waves.
All Tables
Table 1: Passively advected nuclear species.
Table 2:
Dependence of the maximum nickel velocities (in
![]() )
in our two-dimensional models with different spatial resolution
on the width of the polar exclusion cone
)
in our two-dimensional models with different spatial resolution
on the width of the polar exclusion cone
![]() .
.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13431fg1.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg69.png)
|
Figure 1:
Computational workload in the two-dimensional 15 km
resolution model of a supernova explosion as a function of the
logarithm of the simulation time. The number of zones is shown
with a thick solid line ( bottom curve). The simulation begins
with an effective resolution of 15 km which is gradually
decreased with time; at the final time the effective model
resolution is 393 216 km. The wall-clock time per double
time-step is shown with a thin line ( upper curve). Rapid
variations in the wall-clock time are partly due to mesh refinement
( |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13431fg2.epsi}\hspace*{3mm}
\includegraphics[width=7.5cm,clip]{13431fg3.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg71.png)
|
Figure 2:
Supernova shock dynamics in one- and two-dimensional
explosion models. ( Left panel) Evolution of the shock speed
(left scale) as a function of radius in the one-dimensional
(thin) and two-dimensional (medium line) 15 km model. The run of
the mass distribution
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{13431fg4.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg76.png)
|
Figure 3: Density profiles in log scale as a function of the logarithm of the radius in the densest part of the ejecta in one-dimensional models at the final time (t=7 days). Results are shown for models with a resolution of 15 (thick solid), 30 (medium solid), 60 (thin solid), 120 (dotted), and 240 km (dashed line). Note the gradual decrease in the density variation as the mesh resolution increases, which is indicative of numerical convergence. The density profiles of models with a resolution of at least 60 km appear very closely matched. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13431fg5.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg77.png)
|
Figure 4: Evolution of the density in log scale before shock breakout for the one-dimensional explosion model at an effective resolution of 15 km. The initial positions of the Si/O, (C+O)/He, and He/H composition interfaces are marked by dotted vertical lines. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,height=3.7cm,clip]{13431fg6.eps}\p...
...eps}\par\includegraphics[width=8cm,height=3.7cm,clip]{13431fg8.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg94.png)
|
Figure 5: Density distribution in log scale in the 15 km resolution model. ( top) t=4 s; ( middle) t=20 s; ( bottom) t=300 s. Note the presence of two post-SASI bubbles, wrapped in dense metal-rich material, and several triple points (kinks) along the forward shock front at early times; the dense shell features well-developed RTI decorations at t=20 s. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg9.eps}\hspace*{1mm}...
...eps}\hspace*{1mm}
\includegraphics[width=7.6cm,clip]{13431fg12.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg101.png)
|
Figure 6:
Density distribution in log scale in the 15 km resolution
model. (Top left) t=1500 s; ( top right) t=5000 s; (bottom left) t=10 000 s; (bottom right) t=1 day. The polar outflows
are clearly visible at t=5000 s, affecting model
morphology for angles
|
| Open with DEXTER | |
| In the text | |
| |
Figure 7:
Density distribution in log scale in the 15 km
resolution model at t=10 000 s including the supernova
shock. Note the Rayleigh-Taylor instability developing at the
interface between the shocked stellar ejecta and the shocked
wind at a distance
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13431fg14.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg105.png)
|
Figure 8:
Angle-averaged structure of the 15 km model at t=12 h. Shown is the density (thick solid), pressure (medium
solid), radial velocity (thin solid), hydrogen mass fraction
(thin dotted), nickel mass fraction (thick dotted), and ratio of
internal to total energy (thin solid). The RTI-unstable
interface between the shocked ejecta and the shocked stellar
wind is located around
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg15.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg109.png)
|
Figure 9:
Temporal evolution of integrated quantities in
the two-dimensional 15 km resolution model. (Thick solid)
explosion energy; (medium solid) total energy (sum of the
internal and kinetic energy); (thin solid) gravitational energy;
(thin dotted) internal energy; (medium dotted) kinetic energy;
(thick dotted) integrated |
| Open with DEXTER | |
| In the text | |
| |
Figure 10: Density distribution in log scale in the 15 km resolution model at t=7 days. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13431fg17.epsi}\includegraphics[width=7.6cm,clip]{13431fg18.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg113.png)
|
Figure 11:
Angular structure of the 15 km resolution model. (Left panel) radial averages of density (thick solid), pressure (thin solid), radial velocity (thin dotted), and lateral
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg19.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg114.png)
|
Figure 12:
Angular structure of the 15 km resolution model at the
final time. Radial averages are shown for the density (thick solid),
pressure (medium solid), radial velocity (thin solid), and mass
fraction of hydrogen, oxygen, and nickel (dashed, thin dotted,
and thick dotted line, respectively). Radial averages include
only data for distances
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{13431fg20.epsi}\hspace*{4.5mm}
\includegraphics[width=8.2cm,clip]{13431fg21.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg115.png)
|
Figure 13:
Distribution of nickel in the 15 km resolution
model. (Left panel) The angular distribution of the nickel mass
is shown at 0.92 s (thin dotted), 20 s (thick dotted),
300 s (thin solid), 5000 s (medium solid), and t=7 days
(thick solid). Note the fast advection of nickel to the
north pole (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg22.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg121.png)
|
Figure 14:
Mass distribution of the nickel in radial velocity space
in the two-dimensional 15 km resolution model at t=7 days.
Data for different widths of the polar exclusion cone
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13431fg23.epsi}\hspace*{3mm}
\includegraphics[width=7.5cm,clip]{13431fg24.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg122.png)
|
Figure 15:
Composition of the two-dimensional 15 km model at
t=10 000 s. ( Left panel) entire computational domain; ( right panel) |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg25.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg129.png)
|
Figure 16:
Composition in the equatorial section (polar regions
excluded) of the two-dimensional 15 km resolution model at
t=7 days. Mass fractions in log scale are shown as a function
of the radial mass coordinate for hydrogen (thin solid),
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{13431fg26.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg133.png)
|
Figure 17:
Mass distributions in radial velocity space in the
two-dimensional 15 km resolution model at t=7 days. The
distribution of mass is shown for hydrogen (thin solid),
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{13431fg27.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg135.png)
|
Figure 18:
Evolution of the internal to total (internal plus
kinetic) energy ratio in the 15 km resolution model. Radial
averages of the energy ratio are shown at 0.92 s (thin solid),
1500 s (medium solid), 5000 s (thin dotted), 10 000 s
(medium dotted), 12 h (thick solid), and 7 days (thick
dotted). Radial averages include only data for distances
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13431fg28.epsi}\hspace*{4.5mm}
\includegraphics[width=8.05cm,clip]{13431fg29.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg141.png)
|
Figure 19:
Structure of the exploding supernova in the 15 km resolution
models at the final time of t=7 days.
( Left panel) Two-dimensional model. ( Right panel) One-dimensional model. In both panels we show the distributions of
density (thick solid), pressure (medium solid), radial velocity
(thin), hydrogen mass fraction (dashed),
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{13431fg30.epsi}\hspace*{4mm}
\includegraphics[width=8.2cm,clip]{13431fg31.epsi}
\end{figure}](/articles/aa/full_html/2010/13/aa13431-09/Timg142.png)
|
Figure 20: Same as Fig. 14 but for our two-dimensional models with 30 km resolution ( left panel), and 60 km resolution ( right panel). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


