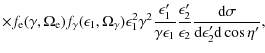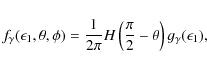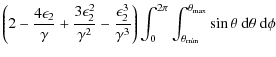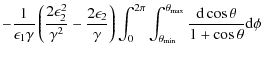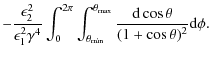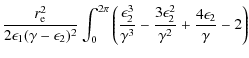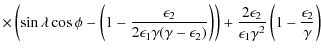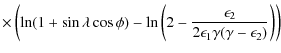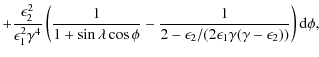| Issue |
A&A
Volume 510, February 2010
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200913190 | |
| Published online | 03 February 2010 | |
Inverse Compton X-rays from relativistic flare electrons and positrons
A. L. MacKinnon - P. C. V. Mallik
Department of Physics and Astronomy, University of Glasgow, Glasgow G12 8QQ, UK
Received 26 August 2009 / Accepted 6 November 2009
Abstract
Context. In solar flares, inverse Compton scattering
(ICS)
of photospheric photons might give rise to detectable hard X-ray photon
fluxes from the corona where ambient densities are too low for
significant bremsstrahlung or recombination. ![]() -ray lines and continuum in
some large flares imply the presence of the necessary
-ray lines and continuum in
some large flares imply the presence of the necessary ![]() 100 MeV
electrons and positrons, the latter as by-products of GeV energy ions.
Recent observations of coronal hard X-ray sources in particular prompt
us to reconsider here the possible contribution of ICS.
100 MeV
electrons and positrons, the latter as by-products of GeV energy ions.
Recent observations of coronal hard X-ray sources in particular prompt
us to reconsider here the possible contribution of ICS.
Aims. We aim to evaluate the ICS X-ray fluxes to be
expected
from prescribed populations of relativistic electrons and positrons in
the solar corona. The ultimate aim is to determine if ICS coronal X-ray
sources might offer a new diagnostic window on relativistic electrons
and ions in flares.
Methods. We use the complete formalism of ICS to
calculate X-ray
fluxes from possible populations of flare primary electrons and
secondary positrons, paying attention to the incident photon angular
distribution near the solar surface and thus improving on the
assumption of isotropy made in previous solar discussions.
Results. Both primary electrons and secondary
positrons produce
very hard ICS X-ray spectra. The anisotropic primary radiation field
results in pronounced centre-to-limb variation in predicted fluxes and
spectra, with the most intense spectra, extending to the highest photon
energies, expected from limb flares. Acceptable numbers of electrons or
positrons could account for RHESSI coronal X/![]() -ray sources.
-ray sources.
Conclusions. Some coronal X-ray sources at least
might be
interpreted in terms of ICS by relativistic electrons or positrons,
particularly when sources appear at such low ambient densities that
bremsstrahlung appears implausible.
Key words: acceleration of particles - radiation mechanisms: general - Sun: corona - Sun: photosphere - Sun: flares - Sun: X-rays, gamma rays
1 Introduction
Korchak (1971,1967) considered three possible radiation mechanisms via which solar flare energetic electrons might produce hard X-rays (HXRs): synchrotron, bremsstrahlung and inverse Compton scattering (ICS). He established that fluxes from electron-ion bremsstrahlung would dominate those from the other two mechanisms under normal solar atmosphere conditions and thus laid one of the foundations of the interpretation of flare X-rays. Left open, however, was the possibility that ICS HXR fluxes from low-density regions might exceed those from bremsstrahlung (or, indeed, recombination - Brown & Mallik 2009,2008). Recent years have seen increasingly detailed observations of coronal HXR sources (Hudson et al. 2001; Tomczak 2009; Krucker et al. 2008b,a), sometimes from surprisingly tenuous regions. Reconsideration of the possible role of ICS in HXR production thus seems timely (Krucker et al. 2008a).The basics of ICS are well understood (e.g. Blumenthal & Gould 1970;
Rybicki
& Lightman 1986). Suppose that electrons of a (total)
energy
![]() scatter photons of an initial energy
scatter photons of an initial energy ![]() .
Optical photons of photospheric origin, for instance,
would have
.
Optical photons of photospheric origin, for instance,
would have ![]() typically of the order of 2 eV. The maximum possible scattered
photon energy results from a head-on
collision of electron and photon and has a value of
typically of the order of 2 eV. The maximum possible scattered
photon energy results from a head-on
collision of electron and photon and has a value of ![]() (e.g. Blumenthal &
Gould 1970). To
produce HXR photons via ICS of optical photons thus needs electrons in
the 10 s to 100 s of MeV energy range.
(e.g. Blumenthal &
Gould 1970). To
produce HXR photons via ICS of optical photons thus needs electrons in
the 10 s to 100 s of MeV energy range.
There is good evidence that electrons attain such energies in
flares. Gamma-ray continuum
radiation in this energy range has been observed from some large flares
(e.g. Forrest
& Chupp 1983; Talon et al. 1993;
Kanbach
et al. 1993).
Electron-ion bremsstrahlung from primary accelerated electrons may
contribute to this feature, as may bremsstrahlung from secondary
electrons and positrons in the 100 MeV energy range, produced
in
reactions of accelerated ions in the energy range
>0.3 GeV
(e.g. Murphy
et al. 1987).
In the latter case, positrons are dominant in number since they result
from collisions between positively charged particles. The continuum
radiation
in this case is unavoidably accompanied by the flat spectral feature
around 70 MeV produced by ![]() decay. High-energy radiation
can occur both with and without this feature at different times during
a single event (e.g. Vilmer
et al. 2003),
indicating that
both primary accelerated electrons and secondary positrons may be
present in the 100 MeV energy range, as needed for ICS HXR
production.
Akimov et al.
(1994) give evidence that the flare of 26 March 1991
accelerated electrons to energies of 300 MeV.
The energy distributions of electrons and positrons will be very
different, however, and we consider them separately.
decay. High-energy radiation
can occur both with and without this feature at different times during
a single event (e.g. Vilmer
et al. 2003),
indicating that
both primary accelerated electrons and secondary positrons may be
present in the 100 MeV energy range, as needed for ICS HXR
production.
Akimov et al.
(1994) give evidence that the flare of 26 March 1991
accelerated electrons to energies of 300 MeV.
The energy distributions of electrons and positrons will be very
different, however, and we consider them separately.
In the presence of the solar magnetic field, these high energy electrons would also produce synchrotron emission, but at radio and sub-mm wavelengths (Silva et al. 2007). To produce X-rays by synchrotron emission would require electrons of unrealistically high energy, for which there is no evidence.
The ICS estimates of Korchak (1971,1967) and Krucker et al. (2008a) employ standard results based on assuming isotropic electron and photon distributions. Electron distributions in the corona may well be isotropic because of pitch-angle scattering by MHD turbulence (e.g. Miller & Ramaty 1989), but the photon distribution will be isotropic only in the outward hemisphere. As already mentioned, the most energetic photons result from head-on collisions of photon and electron, which result in the up-scattered photon travelling along the direction of the incident electron (Jones 1968). These most favourable collisions clearly cannot occur, even with an assumed isotropic coronal electron distribution, so a more involved calculation is essential to evaluate likely ICS fluxes, spectra etc.
ICS is certainly important in other areas of astrophysics: for instance, cosmic microwave background photons are scattered by hot gas in clusters of galaxies (Sunyaev-Zeldovich effect - Sunyaev & Zeldovich 1970) and solar visible photons are scattered by cosmic ray electrons (Orlando & Strong 2008).
The formalism for calculating ICS radiation with arbitrary
photon angular distributions has been given most recently
by Moskalenko &
Strong (2000).
Here we adapt their work to the source geometry near the solar surface.
We use typically
observed power-law distributions of electrons and protons (which
produce secondary positrons) to illustrate our study. We elucidate the
consequences for the observability of this ICS flux and note the
difference between the spectra produced by electrons and by secondary
positrons,
as well as the disc-centre to limb variation. Our findings reveal that
although the ICS intensities are likely to be low, the spectrum is hard
and unmistakable. If detected by modern instruments, this would be a
new window on extremes of electron and ion acceleration at the Sun, and
in the case of ions complementing information available from ![]() -ray lines
and free neutrons detected in space.
-ray lines
and free neutrons detected in space.
In this paper, we use the units ![]() .
.
2 Source geometry; calculation of IC flux
In this section we calculate the ICS HXR fluxes from relativistic electron and positron populations in the corona, following Moskalenko & Strong (2000).
The rate of photon-particle interactions is given in full
generality by (Weaver 1976):
where
To calculate fluxes from Eq. (1),
we need to specify the electron and photon momentum distributions and
the cross-section. Since we
deal with highly relativistic particles and situations where the photon
may carry away a large fraction of the electron energy, we must use the
Klein-Nishina cross-section (e.g. Jauch
& Rohrlich 1976):
where
Appropriately to the general galactic cosmic ray population, Moskalenko & Strong
(2000) assume isotropic electrons;
this assumption will also be appropriate in the corona as a result of
MHD scattering (Mandzhavidze & Ramaty
1992; Miller & Ramaty 1989).
With these assumptions,
the up-scattered photon distribution over the LS energy, ![]() ,
as obtained from Eq. (1)
is (Moskalenko &
Strong 2000)
,
as obtained from Eq. (1)
is (Moskalenko &
Strong 2000)
where
At this point we depart from Moskalenko
& Strong (2000), tailoring our calculation to the
radiation field geometry above the
solar surface (Fig. 1).
We introduce two, spherical polar angular coordinates ![]() and
and ![]() to label photon direction. Let
to label photon direction. Let ![]() be a unit vector pointing
radially outward from the local solar surface, and
be a unit vector pointing
radially outward from the local solar surface, and ![]() be a unit vector pointing along the line of sight to the
observer. Then we have
be a unit vector pointing along the line of sight to the
observer. Then we have ![]() ,
where
,
where ![]() is the heliocentric angle of the source location. Let
is the heliocentric angle of the source location. Let ![]() be
a unit vector in the direction of the
photon. The polar angle
be
a unit vector in the direction of the
photon. The polar angle ![]() measures the angle between
measures the angle between ![]() and
and ![]() ,
i.e.
,
i.e. ![]() .
The photon
azimuthal angle
.
The photon
azimuthal angle ![]() lies in the plane of the solar surface and is measured anticlockwise
from the plane defined by
lies in the plane of the solar surface and is measured anticlockwise
from the plane defined by ![]() and
and ![]() .
.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{13190fg1.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg45.png)
|
Figure 1:
Schematic diagram showing the geometry used to describe the radiation
field at the solar surface with the relevant angles and vectors. |
| Open with DEXTER | |
The photon distribution is isotropic in the optically thick
photosphere, but only includes outward-flowing photons immediately
above. It will be close to
isotropic, in the hemisphere
![]() ,
as long as we consider coronal locations below
,
as long as we consider coronal locations below ![]() .
Thus the photon angular
distribution takes the simple form
.
Thus the photon angular
distribution takes the simple form
where H is the Heaviside step function.
In the first instance we calculate the ICS flux from
monoenergetic electrons with a single energy ![]() ,
averaging straightforwardly over more general
energy distributions as needed. We also consider monoenergetic primary
photon distributions,
,
averaging straightforwardly over more general
energy distributions as needed. We also consider monoenergetic primary
photon distributions, ![]() .
Using Eqs. (2)-(4), we hence find
the total up-scattered photon distribution
per electron over the LS energy,
.
Using Eqs. (2)-(4), we hence find
the total up-scattered photon distribution
per electron over the LS energy, ![]() ,
to be:
,
to be:
The lower limit of the
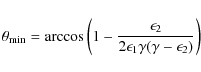
|
(6) |
and the upper limit by source geometry:
| (7) |
Performing the integral over polar angle we get
which is the ICS flux of photons per unit energy per unit time per electron. The following kinematic results (Moskalenko & Strong 2000) are also of importance:
![\begin{displaymath}\epsilon_2'=\epsilon_2/[\gamma(1-\cos\eta')], ~ \epsilon_2\le...
...\epsilon_1'), ~ \epsilon_1'=\epsilon_1\gamma(1+\cos\lambda).\
\end{displaymath}](/articles/aa/full_html/2010/02/aa13190-09/img59.png)
|
(9) |
The maximum energy of the up-scattered photon is
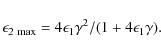
|
(10) |
Note that the second and third terms in Eq. (8) have to be evaluated numerically. This was done using MATLAB, and the results are portrayed in the following section.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg2.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg61.png)
|
Figure 2:
Photon spectra at the Sun (photons per keV per second per source
electron) from limb fast electrons with different power-law
distributions: thin-black is for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg3.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg62.png)
|
Figure 3: Photon spectra at the Sun (photons per keV per second per source electron) from fast electrons with a power-law energy distribution E-3 for an incident photon energy of 200 eV. |
| Open with DEXTER | |
3 Results
3.1 ICS from fast electrons
To calculate ICS spectra produced by relativistic electrons, we assumed
power-law primary electron kinetic energy distributions extending into
the 10s of MeV range,
![]() .
The incident photon population was assumed to have a monoenergetic
energy distribution at
.
The incident photon population was assumed to have a monoenergetic
energy distribution at ![]() eV (or 200 eV in a few,
illustrative cases) so that the solar luminosity implies a photon
density of
eV (or 200 eV in a few,
illustrative cases) so that the solar luminosity implies a photon
density of ![]() .
We have checked that the spectra found using the full,
black body photospheric spectrum are not significantly different from
these shown here for the 2 eV case.
.
We have checked that the spectra found using the full,
black body photospheric spectrum are not significantly different from
these shown here for the 2 eV case.
In Fig. 2
we show the ICS spectra from electrons with an energy spectral index ![]() ,
calculated by weighting the emissivity (8) by this
distribution and integrating over electron energy. Fluxes are
normalised
to one electron above 0.5 MeV, and we assume an upper cutoff
energy of 100 MeV.
The three separate curves signify the ICS spectrum as seen from three
different viewing angles
,
calculated by weighting the emissivity (8) by this
distribution and integrating over electron energy. Fluxes are
normalised
to one electron above 0.5 MeV, and we assume an upper cutoff
energy of 100 MeV.
The three separate curves signify the ICS spectrum as seen from three
different viewing angles ![]() .
In Fig. 3,
we show the ICS spectra for an event viewed at the limb but now for
different values of
.
In Fig. 3,
we show the ICS spectra for an event viewed at the limb but now for
different values of ![]() .
.
Clearly visible (2 eV) photons can easily be
up-scattered
to 10s of keV, even though the actual fluxes and spectra depart
from those expected on the basis of an isotropic photon distribution.
Over most of the photon energy range the spectra are described by the
expected
(e.g. Blumenthal &
Gould 1970) ICS
power-law ![]() ,
but falling off much more steeply as they approach an upper cutoff
determined by the 100 MeV
electron upper cutoff, the viewing angle and the energy spectral index
,
but falling off much more steeply as they approach an upper cutoff
determined by the 100 MeV
electron upper cutoff, the viewing angle and the energy spectral index ![]() .
As expected on geometrical grounds, the most energetic
photons come from limb events. In the photon energy range produced
across the disc, ICS exhibits pronounced limb-brightening with flux
variations
of two orders of magnitude between identical events viewed at the limb
and at disc centre. In Sect. 4
we see that observed coronal source photon fluxes imply plausible
electron numbers.
.
As expected on geometrical grounds, the most energetic
photons come from limb events. In the photon energy range produced
across the disc, ICS exhibits pronounced limb-brightening with flux
variations
of two orders of magnitude between identical events viewed at the limb
and at disc centre. In Sect. 4
we see that observed coronal source photon fluxes imply plausible
electron numbers.
A comparison of the ICS fluxes of Figs. 2 and 3 with the
bremsstrahlung from the same electrons is not quite straightforward.
For the usual monotonic declining energy
distributions of electrons, the bremsstrahlung flux at some photon
energy
![]() is dominated
by electrons with energies just above
is dominated
by electrons with energies just above
![]() .
ICS hard X-ray photons, however, are produced by electrons
in the 10-100 s of MeV energy range. Any comparison
of bremsstrahlung
and ICS fluxes involves an assumption about the electron energy
distribution over a very wide range. There is, for instance, evidence
that electron distributions routinely harden between 10s of keV and the
MeV energy range (e.g. Silva
et al. 2000). Including a bremsstrahlung
spectrum for comparison in Fig. 2
could be quite misleading in
consequence.
.
ICS hard X-ray photons, however, are produced by electrons
in the 10-100 s of MeV energy range. Any comparison
of bremsstrahlung
and ICS fluxes involves an assumption about the electron energy
distribution over a very wide range. There is, for instance, evidence
that electron distributions routinely harden between 10s of keV and the
MeV energy range (e.g. Silva
et al. 2000). Including a bremsstrahlung
spectrum for comparison in Fig. 2
could be quite misleading in
consequence.
For illustration, we may nonetheless assume that a single
power law distribution ![]() in
kinetic energy characterises the electron distribution all the way from
10 keV to 100s of MeV. Adopting
in
kinetic energy characterises the electron distribution all the way from
10 keV to 100s of MeV. Adopting ![]() ,
for example, we find that the bremsstrahlung flux at 10 keV
will be comparable to the ICS flux for an ambient density of about 1010
cm-3. The harder ICS flux will dominate at
photon energies above this value,
until we approach the upper cutoff shown in Fig. 4. Thus ICS
appears likely to dominate
over bremsstrahlung for much of the time in the corona.
,
for example, we find that the bremsstrahlung flux at 10 keV
will be comparable to the ICS flux for an ambient density of about 1010
cm-3. The harder ICS flux will dominate at
photon energies above this value,
until we approach the upper cutoff shown in Fig. 4. Thus ICS
appears likely to dominate
over bremsstrahlung for much of the time in the corona.
Still higher photon energies will result from primary photons
of higher energy. For illustration we show in Fig. 4
the spectrum resulting from ICS of primary
EUV photons of an energy of 200 eV, from a flare at disc centre. For
easy comparison with the results for optical photons we have adopted
the same photon density,
![]() ,
although the true EUV density will be many orders of magnitude smaller
- see below.
,
although the true EUV density will be many orders of magnitude smaller
- see below.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg4.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg72.png)
|
Figure 4:
Photon spectra at the Sun (photons per keV per second per source
electron) from fast electrons with a power-law energy distribution E-3,
where the thin-blue curve is the flux from the disc centre (
|
| Open with DEXTER | |
3.2 ICS from relativistic positrons
As noted in Sect. 1, positrons will be produced as secondaries from fast ion reactions. Electrons and positrons with the same energy distribution would of course produce identical ICS spectra, but the positron energy distribution from p-p collisions and hence the ICS photon spectrum is quite different from the power-law electron case considered in Sect. 3.1. We calculate positron energy distributions as in Vilmer et al. (2003), which in turn closely follows Dermer (1986a,b), assuming they are produced via pion decay following reactions of fast protons with ambient H and He nuclei. The nuclear reactions producing the positrons occur mostly in the chromosphere and photosphere, but with a range of directions. At the energies considered here, any that mirror above the photosphere will suffer only an insignificant energy loss as they make their way into the corona (MacKinnon & Brown 1990). For simplicity, we assume here that we may use the positron energy distribution from pion decay unmodified by any other processes. A more detailed treatment of transport will be carried out elsewhere. We see in Sect. 4 that only a few percent of the number of positrons produced in a large flare will give a detectable ICS source.
Positrons may also be produced in flares via beta decay of unstable nuclei produced in nuclear reactions of flare ions. As noted by Kozlovsky et al. (1987), positrons produced in this way generally have energies of < 1 MeV, too low to be of interest here.
ICS spectra from the resulting positrons are shown in
Fig. 5,
assuming a power-law proton energy distribution with ![]() extending to an upper cutoff energy of 3 GeV and, again,
extending to an upper cutoff energy of 3 GeV and, again, ![]() eV
and
eV
and ![]() cm-3.
Secondary positron distributions have a maximum at
about 300 MeV and a form that is dominated by the nuclear
physics
of pion formation and decay until primary proton energies significantly
exceed
the threshold for pion production (Murphy
et al. 1987).
Thus the detailed photon spectra depend rather weakly on the proton
power-law energy spectral index.
However, certain features persist, i.e. the spectrum remains very hard,
and the most energetic photons will once again come from limb events.
The three separate curves are for three different values of the viewing
angle
cm-3.
Secondary positron distributions have a maximum at
about 300 MeV and a form that is dominated by the nuclear
physics
of pion formation and decay until primary proton energies significantly
exceed
the threshold for pion production (Murphy
et al. 1987).
Thus the detailed photon spectra depend rather weakly on the proton
power-law energy spectral index.
However, certain features persist, i.e. the spectrum remains very hard,
and the most energetic photons will once again come from limb events.
The three separate curves are for three different values of the viewing
angle ![]() .
Also shown is the dashed-green curve in Fig. 5, which is the
bremsstrahlung spectrum from the same positrons, assuming an ambient
density of
.
Also shown is the dashed-green curve in Fig. 5, which is the
bremsstrahlung spectrum from the same positrons, assuming an ambient
density of ![]() .
We
used the cross-section of Bethe and Heitler, without making
non-relativistic or extreme
relativistic approximations (Koch
& Motz 1959, formula 3BN) and the relativistic
electron-electron cross-section of Haug
(1998),
noting that electron-electron and electron-positron cross-sections
become identical for relativistic energies (Haug 1985).
As mentioned above, the form of the positron distribution depends
rather weakly on assumptions about the primary ion distribution, so
this
comparison can be made with much more certainty than for electrons.
Even with this ambient density, fairly high for the corona, ICS
dominates over the bremsstrahlung flux from the same positrons.
Annihilation of positrons in flight yields a continuum photon flux that
may be neglected compared to bremsstrahlung, for present purposes (Murphy et al. 1987).
.
We
used the cross-section of Bethe and Heitler, without making
non-relativistic or extreme
relativistic approximations (Koch
& Motz 1959, formula 3BN) and the relativistic
electron-electron cross-section of Haug
(1998),
noting that electron-electron and electron-positron cross-sections
become identical for relativistic energies (Haug 1985).
As mentioned above, the form of the positron distribution depends
rather weakly on assumptions about the primary ion distribution, so
this
comparison can be made with much more certainty than for electrons.
Even with this ambient density, fairly high for the corona, ICS
dominates over the bremsstrahlung flux from the same positrons.
Annihilation of positrons in flight yields a continuum photon flux that
may be neglected compared to bremsstrahlung, for present purposes (Murphy et al. 1987).
In Fig. 6,
we show the ICS spectra for a range of proton energy distribution ![]() values.
Secondary positron typical energies naturally result in up-scattering
to the MeV photon energy range.
values.
Secondary positron typical energies naturally result in up-scattering
to the MeV photon energy range.
As for the electron case, we would expect a more energetic ICS
flux if we consider incident EUV photons, shown in Fig. 7 for 200 eV
incident photons. With the photon density held fixed, as for
Fig. 5,
the ICS flux can be as much as four orders of magnitude greater for ![]() eV
than
for
eV
than
for ![]() eV, at the same time
extending to higher energies. So we would need an EUV photon density
eV, at the same time
extending to higher energies. So we would need an EUV photon density ![]() times that of visible photons to produce an equally intense ICS flux. A
rough estimate of EUV photon density in a large flare suggests this
will be
times that of visible photons to produce an equally intense ICS flux. A
rough estimate of EUV photon density in a large flare suggests this
will be ![]() ,
however, so low that even the greater fluxes obtained with more
energetic incident photons will not be observable.
,
however, so low that even the greater fluxes obtained with more
energetic incident photons will not be observable.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg78.png)
|
Figure 5:
Photon spectra at the Sun (photons per keV per second per proton) from
relativistic positrons produced by protons with a power-law
energy distribution E-3,
where the thin-blue curve is the flux from the disc centre (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg6.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg79.png)
|
Figure 6:
Photon spectra at the Sun (photons per keV per second per proton) from
limb relativistic positrons produced by protons with different
power-law distributions: thin-blue is for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg7.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg80.png)
|
Figure 7: Photon spectra at the Sun (photons per keV per second per proton) from relativistic positrons produced by protons with a power-law energy distribution E-3 for an incident photon energy of 200 eV. |
| Open with DEXTER | |
4 Comparison with observations
As explained in Sect. 1, ICS could be dominant in producing
HXRs
in low-density regions of the solar atmosphere, which mainly implies
the high corona.
Consider the coronal X/![]() -ray
source in the 2005 January 20 flare, described by Krucker et al. (2008b).
Could it be due to ICS of photospheric photons?
-ray
source in the 2005 January 20 flare, described by Krucker et al. (2008b).
Could it be due to ICS of photospheric photons?
Continuum ![]() -radiation
in the 100 MeV energy range was observed from this flare by
the
SONG instrument on CORONAS-F. There is evidence for a pion decay
contribution to the observed spectrum (Kuznetsov
et al. 2005), which would also
indicate the presence of
-radiation
in the 100 MeV energy range was observed from this flare by
the
SONG instrument on CORONAS-F. There is evidence for a pion decay
contribution to the observed spectrum (Kuznetsov
et al. 2005), which would also
indicate the presence of ![]() MeV
positrons. The flare was located towards the limb (N14
MeV
positrons. The flare was located towards the limb (N14![]() W61
W61![]() ;
;
![]() ),
maximising the likelihood of observable
ICS photons. Moreover, the location of the coronal X-ray source is high
enough that ICS could be the dominant source of HXRs, given sufficient
energetic electrons. The coronal source has a very hard spectrum, of a
photon spectral index
),
maximising the likelihood of observable
ICS photons. Moreover, the location of the coronal X-ray source is high
enough that ICS could be the dominant source of HXRs, given sufficient
energetic electrons. The coronal source has a very hard spectrum, of a
photon spectral index ![]() ,
consistent with the
spectra found in Sect. 3. A photon spectral index of 1.5 would
imply a relativistic electron spectral index of about 2. Continuation
of the photon spectrum
to at least 700-800 keV implies an electron distribution
continuing in this power-law form to at least 120 MeV.
To account for the observed coronal
source fluxes shown in Fig. 3
of Krucker et al.
(2008b), we would need
,
consistent with the
spectra found in Sect. 3. A photon spectral index of 1.5 would
imply a relativistic electron spectral index of about 2. Continuation
of the photon spectrum
to at least 700-800 keV implies an electron distribution
continuing in this power-law form to at least 120 MeV.
To account for the observed coronal
source fluxes shown in Fig. 3
of Krucker et al.
(2008b), we would need ![]() electrons instantaneously present
above 0.5 MeV. The
electrons instantaneously present
above 0.5 MeV. The ![]() keV
source represented by the 50% contour of Krucker et al. (2008b),
Fig. 2c,
is about
keV
source represented by the 50% contour of Krucker et al. (2008b),
Fig. 2c,
is about ![]() arcsec.
Assuming
a similar length scale along the line of sight we estimate its total
volume as
arcsec.
Assuming
a similar length scale along the line of sight we estimate its total
volume as ![]() .
Taking for illustration an
ambient electron density
.
Taking for illustration an
ambient electron density ![]() ,
we see that the relativistic electrons necessary to account for this
source via ICS would represent just
,
we see that the relativistic electrons necessary to account for this
source via ICS would represent just
![]() of all particles in the volume. We also estimate that this is
of all particles in the volume. We also estimate that this is ![]() or less of the electrons > 0.5 MeV implied by a
typical,
large X-ray burst. An uncertain fraction of these would be trapped in
the corona, and the electron distribution might not extend with the
same energy
dependence to 10s of MeV, but it appears quite plausible that enough
electrons
of the required energies are present in the flare. The minimum energy
of 0.5 MeV is of course quite arbitrary; only electrons in the
10s
of MeV range
and above are demanded by an ICS interpretation
of this coronal HXR source.
or less of the electrons > 0.5 MeV implied by a
typical,
large X-ray burst. An uncertain fraction of these would be trapped in
the corona, and the electron distribution might not extend with the
same energy
dependence to 10s of MeV, but it appears quite plausible that enough
electrons
of the required energies are present in the flare. The minimum energy
of 0.5 MeV is of course quite arbitrary; only electrons in the
10s
of MeV range
and above are demanded by an ICS interpretation
of this coronal HXR source.
Close to the limb, the most favourable head-on collisions of electrons with primary photons may occur. The flux and spectrum are very close to those given traditionally for power-law electron distributions and isotropic primary photons (e.g. Blumenthal & Gould 1970; Krucker et al. 2008a), with modifications resulting mostly from the presence of an upper electron cutoff energy. The number and energy distribution of electrons found above are close to those that would be found using the traditional results; but this would not be the case for an event further from the limb.
An interpretation in terms of positrons is also possible. The
spectra shown in Fig. 5
would all give approximately the necessary hard spectrum
in the several hundred keV energy range (although, as discussed above,
none has precisely power-law form). For a power-law primary proton
energy distribution
with an energy spectral index =2, about 1032
protons would be needed above 1 MeV. Masson
et al. (2009) found a proton flux of ![]() cm-3 above
30 MeV for this event and a proton spectral index =3, i.e.
cm-3 above
30 MeV for this event and a proton spectral index =3, i.e. ![]() protons above 1 MeV. Most secondary positrons presumably stop
at
great depths
in the atmosphere, but we would need only a few percent of them to find
their way into the corona in order to account for the coronal HXR
source via ICS.
protons above 1 MeV. Most secondary positrons presumably stop
at
great depths
in the atmosphere, but we would need only a few percent of them to find
their way into the corona in order to account for the coronal HXR
source via ICS.
5 Conclusions and discussion
ICS needs extreme source parameters if it is to account on its own for
the bulk of flare hard X-rays (McClements & Brown 1986;
Korchak
1971),
particularly when `footpoint' source morphology points to an origin in
the dense chromosphere. Our work does not revise this view, just points
out that ICS might be important for understanding sources in the
tenuous corona. We have seen that very modest numbers of electrons or
positrons at
relativistic energies could account for already observed coronal HXR
sources,
even in regions so tenuous that a conventional bremsstrahlung
interpretation would become problematic. Electrons would
need to be accelerated into the 100 MeV energy range;
positrons
are automatically produced with the necessary energies as long as there
are ![]() GeV
protons
to produce them in the first place. The electron distribution needed to
account for HXR bursts, extended into the 100 MeV energy
range,
would include
enough relativistic electrons that only a small fraction of them would
need to be found in the corona to account for at least one observed
coronal
HXR source. Moreover, electrons might be accelerated to relativistic
energies via a process distinct from the main flare energy release, as
appears to occur
in the Earth's magnetosphere (Baker
et al. 2001).
GeV
protons
to produce them in the first place. The electron distribution needed to
account for HXR bursts, extended into the 100 MeV energy
range,
would include
enough relativistic electrons that only a small fraction of them would
need to be found in the corona to account for at least one observed
coronal
HXR source. Moreover, electrons might be accelerated to relativistic
energies via a process distinct from the main flare energy release, as
appears to occur
in the Earth's magnetosphere (Baker
et al. 2001).
How might we distinguish these sources from conventional bremsstrahlung HXRs? First of all, they may be expected from locations where the ambient density seems too low for a conventional bremsstrahlung interpretation. As we have seen, coronal ICS sources should be brightest near the solar limb. If many sources like those described in Krucker et al. (2008b) can be detected, an ICS interpretation would imply a strong centre-to-limb variation. Simultaneous observations from two widely separated spacercraft (e.g. Krucker et al. 2008b) would reveal quite different fluxes and spectra. The spectra will always be very hard, possibly also extending to soft X-ray and EUV ranges in a continuous way difficult to account for by other means. Observations of co-spatial radio radiation would have very different spectral properties in the bremsstrahlung and ICS cases.
Do we need to contain electrons in the corona to produce such sources? The calculations above assume that an isotropic population of electrons is instantaneously present in the source region. Radio observations show coronal containment of high-energy (gyrosynchrotron emitting) electrons (Melnikov et al. 2002; Kundu et al. 2001). The overwhelming contribution to observed ICS, however, comes from electrons moving instantaneously towards the observer. Electrons could pass freely through the corona, following the field lines and emitting observable ICS HXRs as they pass through the line of sight towards the observer. They would not need to be contained in the corona, and an isolated coronal source might be more naturally explained in this way, as a consequence of relativistic beaming and source magnetic geometry. Instantaneous numbers of electrons needed would be comparable to the numbers found above. A more detailed treatment of electron and positron transport, not given here, would be needed to assess this possibility properly.
Our assumed isotropic electron distribution raises similar
questions. We appealed to electron and positron scattering
by MHD turbulence to justify this assumption (e.g. Miller & Ramaty 1989).
It still seems unclear if the coronal electron trapping revealed in
radio is due to turbulence, magnetic field convergence and/or other
physical factors. Electrons may be coronally contained but
anisotropic. The consequences of anisotropy are more easily addressed
for our
highly relativistic electrons than e.g. the study of gyrosynchrotron
radiation carried out by Fleishman
& Melnikov (2003). The cone
of emission about the electron instantaneous direction of motion has
width ![]() ,
so the electron distribution function and the
loop geometry (e.g. orientation north-south; any tilt to the vertical,
etc. - cf. MacKinnon
& Brown 1990) would have to conspire to ensure that
some electrons
travel more or less in the line of sight. Deduced numbers of electrons
would be of the same order of magnitude as those
found assuming isotropy, but the range of viewing angles giving rise to
an observable source would be narrower.
,
so the electron distribution function and the
loop geometry (e.g. orientation north-south; any tilt to the vertical,
etc. - cf. MacKinnon
& Brown 1990) would have to conspire to ensure that
some electrons
travel more or less in the line of sight. Deduced numbers of electrons
would be of the same order of magnitude as those
found assuming isotropy, but the range of viewing angles giving rise to
an observable source would be narrower.
ICS coronal X-ray sources may already have been observed.
Already well-studied
sources, e.g. in the Masuda flare (Masuda
et al. 1994) or some of those described by
Tomczak (2009),
might be reinterpreted in this way. In these smaller events, including
the M class
Masuda flare, there are no ![]() -ray
measurements to give any independent constraint on high-energy
electrons or
positrons, however. In small flares, bright coronal HXR sources in
implausibly tenuous regions would indicate the presence
of relativistic electrons or positrons.
-ray
measurements to give any independent constraint on high-energy
electrons or
positrons, however. In small flares, bright coronal HXR sources in
implausibly tenuous regions would indicate the presence
of relativistic electrons or positrons.
Might ICS yield observable contributions in other wavelength ranges? Flare positrons, for example, would scatter cm wavelength photons into the optical or near UV ranges. In the corona the primary photon number density would be extremely low, making an observable flux highly unlikely, unless the relativistic electrons or positrons lay within an optically thick microwave source. Such a situation would need a much more detailed evaluation of the primary radiation field than we have carried out here, along the lines of McClements & Brown (1986). Other possibilities, like an ICS contribution to the flare UV continuum, appear potentially interesting but would take place in the deeper atmosphere and would similarly require a different treatment of the primary radiation field.
If definitively recognised in flares, ICS coronal HXR sources would open a new window on acceleration and transport of electrons and ions in the 0.1-1 GeV energy range.
AcknowledgementsThe initial impetus for this work came from the I.S.S.I. International Team on ``Coronal Hard X-ray Sources in Solar Flare''. A.L.M. thanks ISSI for hosting the Team; and S. Krucker, H. Hudson and the other participants for discussion. Conversations with T. Porter were also useful. P.C.V.M. is supported by a UK STFC Dorothy Hodgkin's Scholarship. Solar physics research in Glasgow is supported by an STFC Rolling Grant and by the European Union via the SOLAIRE Network (MTRN-CT-2006-035484).
References
- Akimov, V. V., Leikov, N. G., Kurt, V. G., & Chertok, I. M. 1994, in High-Energy Solar Phenomena - a New Era of Spacecraft Measurements, ed. J. Ryan, & W. T. Vestrand, AIP Conf. Ser., 294, 130 [Google Scholar]
- Baker, D. N., Kanekal, S. G., Blake, J. B., & Pulkkinen, T. I. 2001, J. Geophys. Res., 106, 19169 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., & Mallik, P. C. V. 2008, A&A, 481, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. C., & Mallik, P. C. V. 2009, ApJ, 697, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D. 1986a, ApJ, 307, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D. 1986b, A&A, 157, 223 [NASA ADS] [Google Scholar]
- Fleishman, G. D., & Melnikov, V. F. 2003, ApJ, 587, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Forrest, D. J., & Chupp, E. L. 1983, Nature, 305, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Haug, E. 1985, Phys. Rev. D, 31, 2120 [NASA ADS] [CrossRef] [Google Scholar]
- Haug, E. 1998, Sol. Phys., 178, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, H. S., Kosugi, T., Nitta, N. V., & Shimojo, M. 2001, ApJ, 561, L211 [NASA ADS] [CrossRef] [Google Scholar]
- Jauch, J. M., & Rohrlich, F. 1976, The theory of photons and electrons, The relativistic quantum field theory of charged particles with spin one-half, 2nd edn. (New York: Springer) [Google Scholar]
- Jones, F. C. 1968, Phys. Rev., 167, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Kanbach, G., Bertsch, D. L., Fichtel, C. E., et al. 1993, A&AS, 97, 349 [Google Scholar]
- Koch, H. W., & Motz, J. W. 1959, Rev. Mod. Phys., 31, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Korchak, A. A. 1967, SvA, 11, 258 [Google Scholar]
- Korchak, A. A. 1971, Sol. Phys., 18, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Kozlovsky, B., Lingenfelter, R. E., & Ramaty, R. 1987, ApJ, 316, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Battaglia, M., Cargill, P. J., et al. 2008a, A&AR, 16, 155 [Google Scholar]
- Krucker, S., Hurford, G. J., MacKinnon, A. L., Shih, A. Y., & Lin, R. P. 2008b, ApJ, 678, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Kundu, M. R., Nindos, A., White, S. M., & Grechnev, V. V. 2001, ApJ, 557, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Kuznetsov, S. N., Kurt, V. G., Yushkov, B. Y., et al. 2005, in Int. Cosmic Ray Conf., 1, 49 [Google Scholar]
- MacKinnon, A. L., & Brown, J. C. 1990, A&A, 232, 544 [NASA ADS] [Google Scholar]
- Mandzhavidze, N., & Ramaty, R. 1992, ApJ, 389, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Masson, S., Klein, K.-L., Bütikofer, R., et al. 2009, Sol. Phys., 257, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Masuda, S., Kosugi, T., Hara, H., Tsuneta, S., & Ogawara, Y. 1994, Nature, 371, 495 [NASA ADS] [CrossRef] [Google Scholar]
- McClements, K. G., & Brown, J. C. 1986, A&A, 165, 235 [NASA ADS] [Google Scholar]
- Melnikov, V. F., Shibasaki, K., & Reznikova, V. E. 2002, ApJ, 580, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. A., & Ramaty, R. 1989, ApJ, 344, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Moskalenko, I. V., & Strong, A. W. 2000, ApJ, 528, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, R. J., Dermer, C. D., & Ramaty, R. 1987, ApJS, 63, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Orlando, E., & Strong, A. W. 2008, A&A, 480, 847 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Wiley-VCH) [Google Scholar]
- Silva, A. V. R., Wang, H., & Gary, D. E. 2000, ApJ, 545, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, A. V. R., Share, G. H., Murphy, R. J., et al. 2007, Sol. Phys., 245, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1970, Ap&SS, 7, 3 [NASA ADS] [Google Scholar]
- Talon, R., Trottet, G., Vilmer, N., et al. 1993, Sol. Phys., 147, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczak, M. 2009, A&A, 502, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vilmer, N., MacKinnon, A. L., Trottet, G., & Barat, C. 2003, A&A, 412, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weaver, T. A. 1976, Phys. Rev. A, 13, 1563 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
![\begin{figure}
\par\includegraphics[width=5cm,clip]{13190fg1.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg45.png)
|
Figure 1:
Schematic diagram showing the geometry used to describe the radiation
field at the solar surface with the relevant angles and vectors. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg2.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg61.png)
|
Figure 2:
Photon spectra at the Sun (photons per keV per second per source
electron) from limb fast electrons with different power-law
distributions: thin-black is for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg3.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg62.png)
|
Figure 3: Photon spectra at the Sun (photons per keV per second per source electron) from fast electrons with a power-law energy distribution E-3 for an incident photon energy of 200 eV. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg4.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg72.png)
|
Figure 4:
Photon spectra at the Sun (photons per keV per second per source
electron) from fast electrons with a power-law energy distribution E-3,
where the thin-blue curve is the flux from the disc centre (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg5.eps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg78.png)
|
Figure 5:
Photon spectra at the Sun (photons per keV per second per proton) from
relativistic positrons produced by protons with a power-law
energy distribution E-3,
where the thin-blue curve is the flux from the disc centre (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg6.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg79.png)
|
Figure 6:
Photon spectra at the Sun (photons per keV per second per proton) from
limb relativistic positrons produced by protons with different
power-law distributions: thin-blue is for |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13190fg7.ps}
\end{figure}](/articles/aa/full_html/2010/02/aa13190-09/Timg80.png)
|
Figure 7: Photon spectra at the Sun (photons per keV per second per proton) from relativistic positrons produced by protons with a power-law energy distribution E-3 for an incident photon energy of 200 eV. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



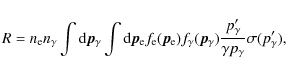
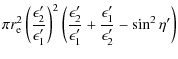
![$\displaystyle \times ~ \delta \left[\epsilon_2' - \frac {\epsilon_1'}{1 + \epsilon_1'(1 - \cos\eta')}\right],$](/articles/aa/full_html/2010/02/aa13190-09/img26.png)