| Issue |
A&A
Volume 511, February 2010
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200912516 | |
| Published online | 12 March 2010 | |
A detailed study of the main sequence of the globular cluster NGC 6397: can we derive constraints on the existence of multiple populations?
M. Di Criscienzo - F. D'Antona - P. Ventura
Osservatorio Astronomico di Roma, via di Frascati 33, 00040, Monte Porzio Catone, Rome, Italy
Received 18 May 2009 / Accepted 15 December 2009
Abstract
Context. Globular clusters can no longer be regarded
as examples of ``simple stellar populations'' as all those so far
examined contain an important fraction of ``second generation'' stars,
in which the light elements are processed through the hot
CNO cycle, and helium variations may be present. Clusters
apparently ``simple'' contain a majority of second generation stars.
Aims. If NGC 6397 contains a large fraction
of ``second generation'' stars (>70% according to
recent analysis), the helium abundance of its stars might also be
affected, show some star-to-star variation, and be larger than the
standard Big Bang abundance ![]() .
Can we derive constraints on this issue from the analysis of the main
sequence width and from its luminosity function?
.
Can we derive constraints on this issue from the analysis of the main
sequence width and from its luminosity function?
Methods. We build up new models for the turnoff
masses and the main sequence down to the hydrogen burning minimum mass,
adopting two versions of an updated equation of state (EOS) including
the OPAL EOS. Models consider different initial helium and
CNO abundances to cover the range of possible variations
between the first and second generation stars. We compare the models
with the observational main sequence. We also make simulations of the
theoretical luminosity function, for different choices of the
mass function and of the mixture of first and second generation stars
and compare them with the observed luminosity function by means of the
Kolmogorov Smirnov - KS-test.
Results. The new models for very low mass stars
compare well with previous models and show that the OPAL EOS is a good
description in all the region of temperature and densities of very low
mass stars for which it is computable. The analysis of the main
sequence width shows that any helium variation must be confined within ![]()
![]() 0.02
in the case of a CNO increase as suggested by literature, and
we discuss the consequent implications for the model of
self-enrichment. We also show that the KS test on the
luminosity functions allows us to derive a best distance modulus for
each age. For a population all made by stars with standard helium Y=0.24,
standard CNO abundances, and an age of 12 Gyr,
choosing a double power law mass function
0.02
in the case of a CNO increase as suggested by literature, and
we discuss the consequent implications for the model of
self-enrichment. We also show that the KS test on the
luminosity functions allows us to derive a best distance modulus for
each age. For a population all made by stars with standard helium Y=0.24,
standard CNO abundances, and an age of 12 Gyr,
choosing a double power law mass function ![]() M-0.7
for M > 0.18
M-0.7
for M > 0.18 ![]() and
and ![]() M-0.9
for M<0.18
M-0.9
for M<0.18 ![]() ,
the resulting theoretical luminosity function agrees well with the
observed one (KS
,
the resulting theoretical luminosity function agrees well with the
observed one (KS ![]() 0.75
for a distance modulus
0.75
for a distance modulus ![]() =
12.31
=
12.31 ![]() 0.05 mag). Using non-standard CNO abundance for all the stars
or for a fraction of 70
0.05 mag). Using non-standard CNO abundance for all the stars
or for a fraction of 70![]() ,
the KS test provides comparable agreement (
,
the KS test provides comparable agreement (![]() KS > 0.55)
with the observed luminosity function.
KS > 0.55)
with the observed luminosity function.
Conclusions. The study of the width of the main
sequence at a different interval of magnitude is consistent with the
hypothesis that both generations are present in the cluster.
If the CNO increase suggested by spectroscopic observation is
taken into account the small helium spread of the main sequence in
NGC 6397 implies a substantial helium uniformity (![]()
![]() 0.02)
between first and second generation stars. The possible spread in
helium doubles if an higher larger increase of CNO is considered. The
luminosity function is in any case well consistent with the observed
data.
0.02)
between first and second generation stars. The possible spread in
helium doubles if an higher larger increase of CNO is considered. The
luminosity function is in any case well consistent with the observed
data.
Key words: stars: general - stars: evolution - stars: low-mass - Hertzsprung-Russell (HR) and C-M diagrams - brown dwarfs
1 Introduction
Our views about globular clusters (GCs) are dramatically changing in recent years, thanks to precise photometric investigations that revealed the presence of multiple main sequences or subgiant branches (e.g. Piotto et al. 2007; Milone et al. 2008) and the increasing amount of new spectroscopic data on GC stars. These data, in particular the spectra for about 2000 stars in 19 GCs recently obtained by the multiobject spectrograph FLAMES@VLT (Carretta et al. 2009a,b) have shown how the ``chemical anomalies'' among GC stars are indeed ubiquitous in all clusters and concern a large fraction (from 50 to 80%) of stars. The peculiar chemical abundances take the form of anticorrelations between O and Na, Al and Mg, and are present in stars of various evolutionary phases (both unevolved main sequence and evolved red giant branch stars) (Gratton et al. 2001; Carretta et al. 2004; Ramírez & Cohen 2002), which supports the idea that they are not due to an ``in situ'' deep mixing in the stars, but have been imprinted in the gas from which they formed, which was polluted by the winds lost by a previous first generation (FG) of stars: according to this hypothesis, we are now seeing a second generation (SG) of stars mixed with the FG. It is not finally settled what kind of stars produced the material that must have been processed by the hot CNO cycle and other proton capture reactions on light nuclei. The two most popular candidates are massive asymptotic giant branch (AGB) stars (e.g. Ventura et al. 2001), and possibly, for the extreme anomalies, super-AGBs (Pumo et al. 2008).Alternative possibilities are massive stars which are either fastly rotating (e.g. Decressin et al. 2007), or in binaries undergoing non-conservative evolution (de Mink et al. 2009).
Carretta et al.
(2009a) examine the famous Na-O anticorrelation and
tentatively divide the stars of each cluster into three groups: the
``primordial'' stars with abundances of O and Na
similar to those found in the halo stars; the ``intermediate'' stars,
which have high Na and a somewhat depleted O; the
``extreme'' stars, which have high Na and a strongly
depleted O. While only a few very massive clusters contain
stars with extreme anomalies, all clusters show a population
with ``intermediate'' chemistry. The problem of GC formation
and early evolution is very complex, but it is easy to accept
that a cluster contains two or multiple populations if it shows both
chemical peculiarities as discussed above, and also photometric
peculiarities: the GC NGC 2808 is a prototype of this
class![]() , as it shows
three populations both in the main sequence (Piotto
et al. 2007) and in its horizontal branch (HB)
extended morphology (D'Antona &
Caloi 2004). It is possible to reproduce these three
populations by assuming that they differ in helium content (e.g. D'Antona & Caloi 2008).
Furthermore, this cluster shows the Na-O anticorrelation in
one of its most extreme forms, with stars reaching very low oxygen
abundances. Carretta
et al. (2006) even find a possible indirect hint of
helium enhancement in the subgroup of oxygen-poor red giants that they
examine. As theory expects that some helium enrichment
accompanies the hot-CNO nucleosynthesis in both the proposed
models (massive AGBs or massive stars), NGC 2808
represents in many respects the most classic example of well-understood
multiple populations in GCs.
, as it shows
three populations both in the main sequence (Piotto
et al. 2007) and in its horizontal branch (HB)
extended morphology (D'Antona &
Caloi 2004). It is possible to reproduce these three
populations by assuming that they differ in helium content (e.g. D'Antona & Caloi 2008).
Furthermore, this cluster shows the Na-O anticorrelation in
one of its most extreme forms, with stars reaching very low oxygen
abundances. Carretta
et al. (2006) even find a possible indirect hint of
helium enhancement in the subgroup of oxygen-poor red giants that they
examine. As theory expects that some helium enrichment
accompanies the hot-CNO nucleosynthesis in both the proposed
models (massive AGBs or massive stars), NGC 2808
represents in many respects the most classic example of well-understood
multiple populations in GCs.
There are other cases, however, in which the presence of
subpopulations is not as clear, and where it is not clear, in
particular, whether the abundance anomalies (in some cases less
prominent,
but always present, according to Carretta
et al. 2009a) are always
accompanied by helium enrichment, nor how large this
enrichment is. The cluster NGC 6397 especially has
always been considered the perfect example of a ``simple stellar
population'' (SSP) due to the ``tightness'' of its HR diagram,
which includes a very compact blue HB. In recent
years, spectacular data for the low main sequence of NGC 6397
have become available. By using the technique of proper motion
cleaning, Richer et al.
(2006) obtained a very tight main sequence and a very clean
luminosity function down to the hydrogen burning minimum mass (HBMM) (Richer et al. 2008).
We decided to use these data to quantify at which level we can
accommodate helium variations in this cluster (and the
possible associated CNO variations), by investigating whether
the main sequence width and its luminosity function are compatible with
a helium spread and/or with a non-standard helium content.
At the same time, we took the opportunity of this comparison
to compute and test new stellar models for the low main sequence.
In these models, we employ and compare new equations of state
(EOS) today available, and we test the available color-
![]() transformations.
transformations.
The outline of the paper is the following. In Sect. 2
we describe in some detail the spectroscopic results concerning the
cluster and what we expect concerning the multiple populations it
should hide and which plausible helium and C+N+O variations
are expected. We then summarize the photometric data by Richer et al. (2008).
After having summarized the literature concerning the low mass main
sequence models, in Sects. 3 and 4 we describe our
code and the results of the computation of solar scaled models; in
Sect. 5 we present ![]() -enhanced models computed for
the comparison with the data for the Globular Cluster
NGC 6397. Both the comparison of the CMD and the luminosity
function with theory are discussed in detail in Sect. 6 also
in the hypothesis of multiple populations with different helium and
possibly also C+N+O, content. In Sect. 7 we
summarize our results and conclusions.
-enhanced models computed for
the comparison with the data for the Globular Cluster
NGC 6397. Both the comparison of the CMD and the luminosity
function with theory are discussed in detail in Sect. 6 also
in the hypothesis of multiple populations with different helium and
possibly also C+N+O, content. In Sect. 7 we
summarize our results and conclusions.
2 The case of NGC 6397: apparently a simple stellar population
Carretta et al. (2009a) find that at least 70% of the stars in the cluster NGC 6397 are ``intermediate'' according to their definition, although photometric studies show that all the evolutionary sequences in this cluster look like those of a prototype SSP: the main sequence is very tight (King et al. 1998; Richer et al. 2006), and the horizontal branch (HB) lacks the extreme HB and blue hook stars that are now regarded as the proof of the presence of a very helium-enriched population (D'Antona et al. 2002; D'Antona & Caloi 2004). The chemical anomalies of the Carretta et al. (2009a) analysis, however, do not come as a complete surprise, as many hints were already available in recent literature about the dubious simplicity of this cluster. First of all, already Bonifacio et al. (2002) had noticed the presence of nitrogen-rich stars that have a normal Lithium content (see also Pasquini et al. 2008), and Carretta et al. (2005) find that only three subgiants out of 14 stars are nitrogen-normal. These features lead us to suspect that the material from which these stars formed is CNO processed, as expected in the stars with low oxygen and high sodium. The possible helium enhancement is certainly not extreme, as are for instance small lithium variations among the turnoff stars (Lind et al. 2009; Korn et al. 2007; Pasquini et al. 2008). In the massive AGB model for the formation of the second generation, the lithium content of the AGB ejecta is not as extremely depleted as in the other models, but it is difficult to believe in a cosmic conspiracy producing exactly the same lithium of the FG, unless the AGB matter is very diluted with FG gas, so that both lithium and helium do not differ too much in the two generations.
A different, mostly theoretical approach led Caloi & D'Antona (2005)
and then D'Antona & Caloi (2008)
to provocatively propose that all the stars in the
clusters which have entirely blue HBs are composed by
SG stars. This idea is at the basis of a possible explanation
of the peculiar difference between the GCs M 3
and M 13. The cluster M 3 has a
complex HB, including many stars redder than the
RR Lyrae (a red clump), RR Lyrae stars,
and a well populated blue side, while M 13,
having the same metallicity, has an only-blue HB. This
difference, which was generally attributed to different age (Rey et al.
2001; Johnson
& Bolte 1998) or to different mass loss along the red
giant branch (Lee
et al. 1994; Catelan et al. 1998)
(the famous second parameter problem) may also be interpreted
by assuming that M 13 is totally deprived of its FG,
and the SG has a minimum helium abundance with a mass fraction of ![]() .
In M 13, whose HB shows a prominent blue
tail, simulations of the HB stellar distribution show that
there must also be a small fraction of stars with helium
.
In M 13, whose HB shows a prominent blue
tail, simulations of the HB stellar distribution show that
there must also be a small fraction of stars with helium ![]() (D'Antona & Caloi 2008).
Is it possible that a GC is composed only
of SG stars? This could indeed happen, as was shown
in some hydrodynamic plus N-body simulations of the
SG formation and of the cluster first phases of dynamical
evolution presented by D'Ercole
et al. (2008). They find that the dynamical
evolution of the cluster may be characterized by an expansion of the
FG star system due to the SNII mass loss
preferentially occurring in the cluster central regions, while the SG
is still forming in the core. Depending on the initial conditions,
the ratio of SG to FG stars may in some cases even
reach a factor of six or more. While this kind of modelling depends on
the input parameters and does not imply that this really occurred in
nature, NGC 6397, with its short blue HB,
a tight main sequence (MS) and red giant branch (RGB) could
indeed be made by a homogeneous set of SG stars, corresponding
to a unique value of Y,
just a larger than the Big Bang abundance (Y
(D'Antona & Caloi 2008).
Is it possible that a GC is composed only
of SG stars? This could indeed happen, as was shown
in some hydrodynamic plus N-body simulations of the
SG formation and of the cluster first phases of dynamical
evolution presented by D'Ercole
et al. (2008). They find that the dynamical
evolution of the cluster may be characterized by an expansion of the
FG star system due to the SNII mass loss
preferentially occurring in the cluster central regions, while the SG
is still forming in the core. Depending on the initial conditions,
the ratio of SG to FG stars may in some cases even
reach a factor of six or more. While this kind of modelling depends on
the input parameters and does not imply that this really occurred in
nature, NGC 6397, with its short blue HB,
a tight main sequence (MS) and red giant branch (RGB) could
indeed be made by a homogeneous set of SG stars, corresponding
to a unique value of Y,
just a larger than the Big Bang abundance (Y ![]() 0.26-0.28).
This speculation would help to understand why the nitrogen abundance in
most of the NGC 6397 stars is quite large. The possibility
that all the stars in this cluster have a homogeneous, but larger than
standard, helium abundance could be falsified by looking at the main
sequence width, which depends on the combination of the photometric
errors with the possible star to star differences in helium.
0.26-0.28).
This speculation would help to understand why the nitrogen abundance in
most of the NGC 6397 stars is quite large. The possibility
that all the stars in this cluster have a homogeneous, but larger than
standard, helium abundance could be falsified by looking at the main
sequence width, which depends on the combination of the photometric
errors with the possible star to star differences in helium.
Apart from this extreme and provocative suggestion, very
recently Carretta
et al. (2009a) show that only up to ![]() 30% of stars
should belong to the primordial population (the FG), under the
assumption that all the stars within three sigma from the lowest sodium
abundance measured in a cluster are ``primordial''
30% of stars
should belong to the primordial population (the FG), under the
assumption that all the stars within three sigma from the lowest sodium
abundance measured in a cluster are ``primordial''![]() .
So at present the most reasonable assumption is that
NGC 6397 has at least 70
.
So at present the most reasonable assumption is that
NGC 6397 has at least 70![]() of SG.
of SG.
Given the sodium and oxygen abundances of the anomalous
cluster stars, do we expect that they have an enhanced helium
content? In the hypothesis that the SG is born from matter
mixed with the hot-CNO processed ejecta of massive AGBs, we can look at
the results by Ventura &
D'Antona (2009). They interpret the anomalous
Na-O abundances in NGC 6397 as a result of
mixing between 50% of pristine gas with 50% of gas
ejected by the 5 ![]() AGBs. Looking at
Table 2
of their paper, the helium abundance in the 5
AGBs. Looking at
Table 2
of their paper, the helium abundance in the 5 ![]() ejecta for Z=0.0006 is Y=0.329.
A dilution by 50% with matter that has primordial Y=0.24
provides indeed Y=0.285. If we take these
results at face value, the total CNO content of the
SG stars is also higher than that of the FG stars.
The 5
ejecta for Z=0.0006 is Y=0.329.
A dilution by 50% with matter that has primordial Y=0.24
provides indeed Y=0.285. If we take these
results at face value, the total CNO content of the
SG stars is also higher than that of the FG stars.
The 5 ![]() AGB evolution provides a CNO enhancement by
a factor of about three, so we must also consider increased
CNO (and total metallicity) by a factor
of 1.5 when we compute the higher helium models.
Of course, the computed AGB models do not give a
mandatory prescription of what really happens in the cluster,
so that we will also consider normal CNO models and
models with even larger CNO to include all possible cases. Helium
abundances equal to or larger than the standard ones will be considered
up to Y=0.28, to understand whether the
hypothesis that at least
AGB evolution provides a CNO enhancement by
a factor of about three, so we must also consider increased
CNO (and total metallicity) by a factor
of 1.5 when we compute the higher helium models.
Of course, the computed AGB models do not give a
mandatory prescription of what really happens in the cluster,
so that we will also consider normal CNO models and
models with even larger CNO to include all possible cases. Helium
abundances equal to or larger than the standard ones will be considered
up to Y=0.28, to understand whether the
hypothesis that at least ![]() % of stars in
NGC 6397 have an helium abundance larger than the Big Bang
abundance is consistent with the photometric data.
% of stars in
NGC 6397 have an helium abundance larger than the Big Bang
abundance is consistent with the photometric data.
2.1 The observational color-magnitude diagram of globular cluster NGC 6397
The first HST observations of the low MS of NGC 6397 date back to Paresce et al. (1995). Afterwards, King et al. (1998) have observed NGC 6397 with WFPC2@HST and found that the luminosity function has a rapid decline at low mass end. Recently, the most thorough observations by Richer et al. (2006,2008) refined the data. They observed an outer region of NGC 6397 with ACS@HST using the photometric filters F814W and F606W. The high sensitivity of the camera, the large number of orbits obtained (=126) and the vicinity of the cluster (it is the second closest globular cluster, after M4) made it possible to reach the deepest intrinsic luminosities for a globular cluster achieved until today and what appears as the termination of the MS. The field observed overlaps that of archival WFPC2 data from 1994 and 1997, which were used for the proper-motion-cleaning of the data. This technique, applied to the deep ACS photometry, produces a very narrow MS till its end. These observations are a good basis to test the physics of low mass stars and the possible role of the helium abundance. Richer et al. (2008) analyzed the color-magnitude diagram (CMD) using the results of models computed with the Dartmouth Stellar Evolution Program (DSEP) (Dotter et al. 2007). Their main results are that
- the MS appears to terminate close to the CMD location of the HBMM predicted by models. The authors state that they would have found fainter MS stars in the cluster, if there had been any;
- the MS fitting technique provides a good agreement down to F814W =
22.5 mag; below this, down to
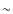 24 mag, the isochrone is either too blue
or too low in luminosity. The authors underline that this is likely due
to low mass models being less luminous at a given mass than real stars;
24 mag, the isochrone is either too blue
or too low in luminosity. The authors underline that this is likely due
to low mass models being less luminous at a given mass than real stars;
- exploring the MS luminosity function, they find that a power law for the mass function MF well reproduces the distribution in luminosity of the observed stars, while a more top-heavy MF is necessary to fit the data in the cluster core that they also have available. However, theory predicts more stars than observed at the lowest MS luminosities, as also previously found by Montalban et al. (2000) using data by King et al. (1998).
3 The low mass main sequence models: input physics of the models
The computation of very low mass stellar models requires an accurate
knowledge of the EOS for partially ionized gas at densities where the
ideal gas EOS approximations breaks down dramatically,
especially close to the pressure ionization region (Saumon
et al. 1995; Fontaine et al. 1977; Magni &
Mazzitelli 1979). The general properties of very low masses
have been described in many works (for example see the reviews by Chabrier
& Baraffe 1997; Alexander et al. 1997;
Cassisi
et al. 2000); for the population II low
masses, after the work by D'Antona
(1987), based on grey atmosphere boundary conditions and on
the EOS by Magni & Mazzitelli
(1979), Baraffe
et al. (1997) presented models based on the Saumon et al. (1995)
EOS and on the NextGen non-grey atmosphere models later on published by
Hauschildt et al. (1999).
They showed that this latter improvement was essential to reproduce the
colors of the low mass main sequence. Montalban
et al. (2000), reexamining the problem of the EOS,
cautioned about the use of the additive volume interpolation needed to
obtain the thermodynamic quantities for intermediate compositions from
the pure hydrogen and pure helium tables available in the Saumon et al. (1995)
EOS. In recent years, two new EOS have become available: the
FreeEOS by Irwin (2004)![]() and the OPAL EOS, namely the EOS provided by the Livermore
group as a byproduct of the opacity computation (Rogers et al. 1996).
Both EOS do not cover the pressure ionization region however,
for which the best approach remains that by Saumon et al. (1995).
The FreeEOS has been recently employed by Dotter et al. (2007)
and applied to the fit of the main sequence of NGC 6397. The
OPAL EOS has not yet been used to approach the construction of low mass
models, so we decided to adopt it in two different ways in our new
models, as described in Sect. 4.
and the OPAL EOS, namely the EOS provided by the Livermore
group as a byproduct of the opacity computation (Rogers et al. 1996).
Both EOS do not cover the pressure ionization region however,
for which the best approach remains that by Saumon et al. (1995).
The FreeEOS has been recently employed by Dotter et al. (2007)
and applied to the fit of the main sequence of NGC 6397. The
OPAL EOS has not yet been used to approach the construction of low mass
models, so we decided to adopt it in two different ways in our new
models, as described in Sect. 4.
We use the ATON code for stellar evolution; a detailed description can be found in Ventura et al. (2007); below we recall the main updated inputs that are important for the treatment of low mass stars.
3.1 Opacities and nuclear reaction
The program includes the opacities by Ferguson
et al. (2005) for the external region of the star (T ![]() 15 000 K)
and the latest version (2005) of OPAL opacities for higher
temperatures (Iglesias &
Rogers 1996). For fully convective low mass stars
(below
15 000 K)
and the latest version (2005) of OPAL opacities for higher
temperatures (Iglesias &
Rogers 1996). For fully convective low mass stars
(below ![]() 0.35
0.35 ![]() )
the uncertainties on radiative opacities have negligible influence on
the models, while for larger masses an error in opacity by
)
the uncertainties on radiative opacities have negligible influence on
the models, while for larger masses an error in opacity by ![]() 20
20![]() may cause an error up to
may cause an error up to ![]() 1
1![]() in the determination of radii (Dotter
2007). Electron conduction opacities were taken from the WEB
site of Potekhin (2006) and correspond to the Potekhin et al. (1999)
treatment, corrected following the improvement of the treatment of the
e-e scattering contribution described in Cassisi et al. (2007).
in the determination of radii (Dotter
2007). Electron conduction opacities were taken from the WEB
site of Potekhin (2006) and correspond to the Potekhin et al. (1999)
treatment, corrected following the improvement of the treatment of the
e-e scattering contribution described in Cassisi et al. (2007).
Although not necessary in this computation, the nuclear
network includes 30 chemical elements, all main
reactions of p-p, CNO, Ne-Na and Mg-Al chains and the ![]() capture
of all nuclei up 26Mg. The relevant cross
sections are from the NACRE compilation (Angulo et al. 1999).
capture
of all nuclei up 26Mg. The relevant cross
sections are from the NACRE compilation (Angulo et al. 1999).
3.2 Equation of state: OPAL vs. Saumon et al. (1995)
As remarked previously, non-ideal effects become increasingly important
for masses M ![]() 0.8
0.8 ![]() .
.
ATON uses 18 tables of EOS in the (gas)pressure-temperature
plane corresponding to three different metallicities, Z=0,
0.02 and 0.04, and six hydrogen mass fractions X,
ranging from 0 to 1-Z; the
thermodynamic quantities, i.e. density, adiabatic gradient,
specific heat at constant pressure Cp,
the Cp/Cv ratio,
and the three exponents ![]() ,
,
![]() and
and ![]() are obtained via four cubic unidimensional splines on X,
Z, pressure and temperature.
are obtained via four cubic unidimensional splines on X,
Z, pressure and temperature.
These 18 tables are constructed up in three steps. First, the thermodynamic quantities are computed according to the formulation by Stolzmann & Blöcker (2000), which is the most modern and updated description available for ionized gas, including both classic and relativistic degeneracy, coulombian effects and exchange interaction. The tables are then partially overwritten by the OPAL EOS in the whole domain where this is available (Rogers et al. 1996, see OPAL WEB page, last update in February 2006). Finally in the very low-temperature regime, where OPAL EOS is not available (see Fig. 1) the tables are overwritten by the Saumon et al. (1995) EOS, which has the advantage of employing an adequate physical model for the pressure ionization. The Saumon et al. EOS is only given for pure hydrogen and pure helium mixtures; the presence of metals is thus simulated by adding helium, and the different H-He mixtures must be interpolated through the additive volume law.
We call ``EOS+OPAL'' the tables that represent the standard in
our computations. To investigate how the results depend on the
chosen EOS, we built additional tables (EOS+SCH) using the EOS by Saumon et al. (1995, SCH)
in the whole region of the ![]() plane for which it
is available. This is an interesting test, because the structure of the
majority of stars discussed here are contained in the region of plane
plane for which it
is available. This is an interesting test, because the structure of the
majority of stars discussed here are contained in the region of plane ![]() where both EOS are available (see Fig. 1).
where both EOS are available (see Fig. 1).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12516f1.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg32.png)
|
Figure 1:
We show the region of the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12516f2.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg33.png)
|
Figure 2:
Adiabatic gradient (
|
| Open with DEXTER | |
In Fig. 2
we show the differences in the molecular weight (![]() )
and adiabatic gradient
)
and adiabatic gradient ![]() =
= ![]() along the structure of two main sequence models of
along the structure of two main sequence models of ![]() ,
Z=0.0006 at the age of 10 Gyr, computed
with the two different EOS. The differences are more evident
in the zone of partially ionization where physical differences of the
two treatments (different
,
Z=0.0006 at the age of 10 Gyr, computed
with the two different EOS. The differences are more evident
in the zone of partially ionization where physical differences of the
two treatments (different ![]() )
affect
)
affect
![]() .
In the EOS+SCH models, the regions in which
.
In the EOS+SCH models, the regions in which ![]() is lower prevail, and the global effect is to produce
is lower prevail, and the global effect is to produce ![]() larger by about 100 K practically at the same luminosity,
since the inner structure does not change significantly with
the EOS.
larger by about 100 K practically at the same luminosity,
since the inner structure does not change significantly with
the EOS.
The results for different masses are shown in Fig. 3, reporting the
HR location of the models at 10 Gyr. The differences
are small for M ![]() 0.5
0.5 ![]() ,
where the regions of partial ionization do not dominate, and vanish at
the lowest masses, because only the EOS+SCH is available for the
physical conditions of their interiors.
,
where the regions of partial ionization do not dominate, and vanish at
the lowest masses, because only the EOS+SCH is available for the
physical conditions of their interiors.
Based on these results, we may conclude that use of both EOS
leads to models with compatible effective temperatures and
luminosities. In Fig. 3 we report the
location of the models of same chemistry computed by Dotter et al. (2007)
for the available masses, with the Dartmouth Stellar Evolution Program
(DSEP), using the FreeEOS by Irwin (2004)![]() and otherwise very similar input physics (L
and
and otherwise very similar input physics (L
and
![]() 's are taken from their
WEB page); for the same masses the models by Baraffe et al. (1997)
are also shown. Note that these latter models do not differ
significantly from ours both in L
and
's are taken from their
WEB page); for the same masses the models by Baraffe et al. (1997)
are also shown. Note that these latter models do not differ
significantly from ours both in L
and
![]() ,
while the models calculated with DSEP at the lowest masses differ,
especially in
,
while the models calculated with DSEP at the lowest masses differ,
especially in
![]() ,
up to
,
up to ![]() 300 K
at 0.15
300 K
at 0.15 ![]() .
This effect can be possibly attributed to the different EOS, but a
detailed comparison of models would be required.
.
This effect can be possibly attributed to the different EOS, but a
detailed comparison of models would be required.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12516f3.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg37.png)
|
Figure 3: HR diagram location at 10 Gyr for models with Z=0.0006, the labelled masses are calculated with different EOS tables. Models from the Dartmouth Stellar Evolution Database (full dots) and from Baraffe et al. (1997) (asterisks), with the same metallicity as ours, are also shown for comparison. |
| Open with DEXTER | |
3.3 Convection
The ATON code allows us to model turbulent convection by adopting the traditional Mixing Lenght Theory (MLT, Bohm-Vitense 1958) or the ``Full Spectrum of Turbulence'' (FST) model (Canuto & Mazzitelli 1991; Canuto et al. 1996) which takes into account the full eddies energy distribution (see Canuto & Mazzitelli 1991, for a detailed description of the physical differences between the two models).
While for very low mass stars the description of convection
has no influence on the atmospheric structure, this does not
hold for those masses in which convection has a substantial degree of
overadiabaticity, especially for the stars at the turnoff of GCs. For
these models a homogeneous modelling of convection in the atmosphere
and the interior is highly recommended. At
![]() > 4000 K,
the grids of models computed by Heiter
et al. (2002) by means of NEMO, a modified version
of Kurucz's code, are available. These grids are provided both with the
MLT model and with the FST model by Canuto et al. (1996).
A preliminary version of these latter grids has been used by Montalbán et al. (2001)
and will be used in this paper (where possible).
> 4000 K,
the grids of models computed by Heiter
et al. (2002) by means of NEMO, a modified version
of Kurucz's code, are available. These grids are provided both with the
MLT model and with the FST model by Canuto et al. (1996).
A preliminary version of these latter grids has been used by Montalbán et al. (2001)
and will be used in this paper (where possible).
3.4 Atmospheric structure and boundary condition
At ![]()
![]() 4000 K in the outermost layers of very low mass stars,
radiative absorption is dominated by molecules, and the outcoming flux
is very different from the frequency-averaged distribution provided by
grey models (Montalban
et al. 2000; Baraffe et al. 1997).
At larger
4000 K in the outermost layers of very low mass stars,
radiative absorption is dominated by molecules, and the outcoming flux
is very different from the frequency-averaged distribution provided by
grey models (Montalban
et al. 2000; Baraffe et al. 1997).
At larger
![]() ,
the atmospheric models become less critical, whereas the
,
the atmospheric models become less critical, whereas the ![]() itself is heavily influenced by the treatment of overadiabatic
convection. For the non-grey models that employ an
MLT treatment of convection in the atmosphere with a
given
itself is heavily influenced by the treatment of overadiabatic
convection. For the non-grey models that employ an
MLT treatment of convection in the atmosphere with a
given
![]() ,
not only the
,
not only the ![]() used in the interior computation (
used in the interior computation (
![]() )
affects the
)
affects the
![]() ,
but also the optical depth at which the match between the atmospheric
and the interior integration is made, and also the value of
,
but also the optical depth at which the match between the atmospheric
and the interior integration is made, and also the value of
![]() (Montalbán et al. 2004).
Montalbán et al. (2001)
have shown that the use of the NEMO grids of model atmospheres
(Heiter et al. 2002)
computed with the FST convection may provide a good match to
the interior models computed with the same convection model in the
interior, independently of the matching optical depth.
(Montalbán et al. 2004).
Montalbán et al. (2001)
have shown that the use of the NEMO grids of model atmospheres
(Heiter et al. 2002)
computed with the FST convection may provide a good match to
the interior models computed with the same convection model in the
interior, independently of the matching optical depth.
For the above two reasons we use boundary conditions according
to the stellar mass based on two different grids of non-grey models of
atmosphere![]() . For M
. For M ![]() 0.5
0.5 ![]() we use Heiter et al. (2002)
FST grids and also FST convection in the interior
computations, whereas for M
we use Heiter et al. (2002)
FST grids and also FST convection in the interior
computations, whereas for M ![]() 0.5
0.5 ![]() we adopt the NextGen grids by Hauschildt
et al. (1999) computed by the PHOENIX code with the
MLT treatment of convection and
we adopt the NextGen grids by Hauschildt
et al. (1999) computed by the PHOENIX code with the
MLT treatment of convection and ![]() .
The available grids extend down to
.
The available grids extend down to ![]() = 800 K
for the [M/H] = -2.0 models, but just down
to 2000 K for larger metallicity. For these M
= 800 K
for the [M/H] = -2.0 models, but just down
to 2000 K for larger metallicity. For these M ![]() 0.5
0.5 ![]() models, we adopt MLT convection also in the interior
computation, setting
models, we adopt MLT convection also in the interior
computation, setting ![]() =
2.0
=
2.0![]() . Since the model
atmospheres are computed assuming an ideal gas and Saha-like
thermodynamics, they should not be used in the real gas domain where
pressure effects are relevant. A relatively small value of the
optical depth is chosen for the match
between atmosphere and interior. We use
. Since the model
atmospheres are computed assuming an ideal gas and Saha-like
thermodynamics, they should not be used in the real gas domain where
pressure effects are relevant. A relatively small value of the
optical depth is chosen for the match
between atmosphere and interior. We use ![]() =
3(10) for
=
3(10) for ![]() .
Notice that the grids of model atmospheres available are computed only
for solar scaled mixtures. The lack of suitable model atmospheres for
.
Notice that the grids of model atmospheres available are computed only
for solar scaled mixtures. The lack of suitable model atmospheres for ![]() -enhanced
populations forces us to use a grid for the boundary atmospheric
conditions with larger [Fe/H] to simulate the
-enhanced
populations forces us to use a grid for the boundary atmospheric
conditions with larger [Fe/H] to simulate the ![]() -enhancement,
following the procedure adopted by Baraffe
et al. (1997). We use a grid for
[Fe/H] = -1.7, obtained through interpolation between
the grids for [Fe/H] = -2.0 and -1.5,
to compute
-enhancement,
following the procedure adopted by Baraffe
et al. (1997). We use a grid for
[Fe/H] = -1.7, obtained through interpolation between
the grids for [Fe/H] = -2.0 and -1.5,
to compute ![]() -enhanced
models with Z=0.0002.
-enhanced
models with Z=0.0002.
3.5 Transformations to observational plane
In order to compare the models to the photometric data in
NGC 6397 we convert luminosity, ![]() and surface gravity into absolute magnitudes and colors in the
ACS filters. The method most used is to calculate theoretical
stellar spectra from atmosphere models and to convolve these synthetic
spectra with the filter transmission curves for a photometric system
which defines the transmission of light through the filter as a
function of wavelength. Uncertainties derive especially from the
missing or incorrect absorption features and simplifying physical laws
as the assumption of LTE. On the other hand, semiempirical
colors and bolometric corrections (e.g. Vandenberg
& Clem 2003) have other uncertainties,
e.g. they depend on the assumed distance (Dotter et al. 2007).
and surface gravity into absolute magnitudes and colors in the
ACS filters. The method most used is to calculate theoretical
stellar spectra from atmosphere models and to convolve these synthetic
spectra with the filter transmission curves for a photometric system
which defines the transmission of light through the filter as a
function of wavelength. Uncertainties derive especially from the
missing or incorrect absorption features and simplifying physical laws
as the assumption of LTE. On the other hand, semiempirical
colors and bolometric corrections (e.g. Vandenberg
& Clem 2003) have other uncertainties,
e.g. they depend on the assumed distance (Dotter et al. 2007).
For the specific case of ACS filters, we use the procedure by Bedin et al. (2005).
They computed ACS color indices by using a homogeneous set of
ODFNEW model atmospheres and synthetic fluxes computed with
the Kurucz ATLAS9 code (Castelli
& Kurucz 2003). Grids of magnitudes for different
values of [Fe/H], for 3500 K ![]()
![]()
![]() 50 000 K, 0
50 000 K, 0 ![]()
![]()
![]() 5.0 and microturbolent velocity 2.0 km s-1
are provided. Visual bolometric correction BC
5.0 and microturbolent velocity 2.0 km s-1
are provided. Visual bolometric correction BC![]() ,
visual magnitude
,
visual magnitude ![]() ,
and color indices
,
and color indices
![]() are given. The ACS magnitudes were computed by using the
WFC/ACS transmission curves by Sirianni
et al. (2005), while they adopted the V passband
from Bessel (1990).
Finally, they assumed that the Vega ACS magnitude would be
equal to 0.00 in all passbands.
are given. The ACS magnitudes were computed by using the
WFC/ACS transmission curves by Sirianni
et al. (2005), while they adopted the V passband
from Bessel (1990).
Finally, they assumed that the Vega ACS magnitude would be
equal to 0.00 in all passbands.
The bolometric corrections by Bedin
et al. (2005) for ACS filters do not extend
below
![]() = 3500 K.
For these low temperatures we can use the values obtained from the
synthetic spectra of Hauschildt
et al. (1999). In this case the transmission filters
of Sirianni et al. (2005)
were used as well, and zero point corrections to standard systems are
obtained from observed Vega spectra.
= 3500 K.
For these low temperatures we can use the values obtained from the
synthetic spectra of Hauschildt
et al. (1999). In this case the transmission filters
of Sirianni et al. (2005)
were used as well, and zero point corrections to standard systems are
obtained from observed Vega spectra.
Obviously the availability of a unique set of colors-
![]() transformations would be highly recommended; but for masses below
0.5
transformations would be highly recommended; but for masses below
0.5 ![]() ,
we have at least the advantage t use the
same bolometric corrections derived from the atmospheric structures
used as boundary conditions for the stellar models.
,
we have at least the advantage t use the
same bolometric corrections derived from the atmospheric structures
used as boundary conditions for the stellar models.
Finally we note that the two sets of correlations match very well in the main sequence, so that no discontinuity arises in our transformed isochrones.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12516f4.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg49.png)
|
Figure 4: Evolutionary tracks, starting from the pre-main-sequence, for three different masses with Z=0.0006 and the different value of initial helium.The filled circle labels the position in the HR diagram of the star at age = 10 Gyr. Only for the highest mass the tracks with the all three Y are shown. |
| Open with DEXTER | |
4 Results: solar scaled models
We computed evolutionary tracks for low mass objects (M ![]() 0.8
0.8 ![]() )
from the pre-main sequence to the red giant branch, or until
they reach an age of 20 Gyr. Results are shown here for
[M/H] = -1.5 and [M/H] = -2.0,
but larger metallicities ([M/H] = -1.00
and -0.50) are available upon request.
)
from the pre-main sequence to the red giant branch, or until
they reach an age of 20 Gyr. Results are shown here for
[M/H] = -1.5 and [M/H] = -2.0,
but larger metallicities ([M/H] = -1.00
and -0.50) are available upon request.
In this section we present results for solar scaled mixtures (Grevesse & Sauval 1999,
GS1999), [![]() /Fe] =
0.4 models will be used in Sect. 6 to compare with
the data of NGC 6397. Models are extended down to the HBMM
when the atmospheric boundary conditions allow for it.
/Fe] =
0.4 models will be used in Sect. 6 to compare with
the data of NGC 6397. Models are extended down to the HBMM
when the atmospheric boundary conditions allow for it.
We computed standard evolutionary tracks with an initial helium content close to the Big Bang abundance (that is Y=0.24, Coc et al. 2004) and models with larger helium (Y=0.28, 0.32 and 0.40). From the evolutionary tracks, isochrones are derived for typical ages expected for GCs, from 10 to 14 Gyr.
Figure 4
compares the HR diagram evolution for three different masses (M=0.70,
0.30 and 0.10 ![]() )
and different Y. Models with a larger
helium abundance have larger luminosity and
)
and different Y. Models with a larger
helium abundance have larger luminosity and ![]() due to the on average greater mean molecular weight
due to the on average greater mean molecular weight ![]() .
This effect is more evident in the stars with a radiative core (shown
heare is the M=0.7
.
This effect is more evident in the stars with a radiative core (shown
heare is the M=0.7 ![]() )
than in the completely convective stars like the 0.3
)
than in the completely convective stars like the 0.3 ![]() .
The difference increases again in the lowest masses (
.
The difference increases again in the lowest masses (![]() 0.15
0.15 ![]() ), where
partial degeneracy begins to play a role.
), where
partial degeneracy begins to play a role.
4.1 Mass-luminosity relation
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12516f5.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg50.png)
|
Figure 5: The MLR for models at 10 Gyr having the labelled value of metallicity and different helium abundance (=0.24-open circles, =0.28-filled triangles, =0.32-filled circles, =0.40-asterisks). In each case the lower masses are the derived HBMM and reported in Table 1. |
| Open with DEXTER | |
The mass-luminosity relation (MLR) is essential for the comparison with the data, as it enters in the conversion of the (assumed) mass function into the luminosity function (LF).
Any change of slope of the MLR will be reflected in the
luminosity function, which is defined as ![]()
![]()
![]() .
Where the MLR presents an inflection point, the LF has a
relative maximum or minimum. As the luminosity decreases along
the MS, there are two inflection points, responsible for two
main peaks in the LF (see Fig. 7): the first,
at
.
Where the MLR presents an inflection point, the LF has a
relative maximum or minimum. As the luminosity decreases along
the MS, there are two inflection points, responsible for two
main peaks in the LF (see Fig. 7): the first,
at
![]()
![]() 6 mag, is due to the transition between pure
MS models and models that suffer the effects of evolution
(and are more luminous in the MS due to the hydrogen
consumption). Therefore, the corresponding peak in the LF is a function
of age, and also as we will see, of Y.
After a small range of homologous models, the MLR steepens
progressively due to the onset of molecular absorption in the stellar
envelope; this produces a
gradual increase in the LF. When models become fully convective at
6 mag, is due to the transition between pure
MS models and models that suffer the effects of evolution
(and are more luminous in the MS due to the hydrogen
consumption). Therefore, the corresponding peak in the LF is a function
of age, and also as we will see, of Y.
After a small range of homologous models, the MLR steepens
progressively due to the onset of molecular absorption in the stellar
envelope; this produces a
gradual increase in the LF. When models become fully convective at ![]() 0.35
0.35 ![]() ,
the MLR relation begins to flatten again, and the presence of
this inflection point results in the large peak at
,
the MLR relation begins to flatten again, and the presence of
this inflection point results in the large peak at ![]()
![]() 8 mag, which is present in all the GC LFs (D'Antona 1998) and is shown
in Fig. 7.
8 mag, which is present in all the GC LFs (D'Antona 1998) and is shown
in Fig. 7.
Finally, at masses M ![]() 0.12
0.12 ![]() ,
the MLR relation flattens even more. This is due to
the onset of degeneracy in the core of the star (D'Antona 1998), and this
subsequent decrease in the LF is dependent on the EOS. The
HR diagram does not show the minute features of the MLR
derivative, but it shows two ``kinks'', the first one
corresponding to the onset of molecular hydrogen dissociation in the
envelope (Copeland et al.
1970) and the second to the onset of degeneracy.
,
the MLR relation flattens even more. This is due to
the onset of degeneracy in the core of the star (D'Antona 1998), and this
subsequent decrease in the LF is dependent on the EOS. The
HR diagram does not show the minute features of the MLR
derivative, but it shows two ``kinks'', the first one
corresponding to the onset of molecular hydrogen dissociation in the
envelope (Copeland et al.
1970) and the second to the onset of degeneracy.
In Fig. 5 we show the dependence of the MLR on the metallicity and helium content at 10 Gyr. Y mostly influences the evolved part of MS and the location of the very low masses, where degeneracy sets in and the second MS kink is located. At the MS end, decreasing the mass, the higher helium models remain more luminous and hotter. These features will affect the low luminosity LF, which will decrease more slowly with decreasing luminosity for larger Y. At the brightest MS luminosities, the larger the Y, the smaller the slope of the MLR of those models that partially burn their hydrogen during a Hubble time with respect to the case of Y=0.24. This is an obvious feature of the evolutionary models: larger Y produces larger MS luminosities and faster MS evolution.
The quantitative results concerning the lowest luminosities
will also depend on the EOS, as we can easily understand by
comparing the MLR relations obtained using EOS+OPAL and
EOS+SCH tables (Fig. 6).
For masses larger than 0.1 ![]() the models using EOS+SCH are slightly more luminous as a consequence of
the differences in
the models using EOS+SCH are slightly more luminous as a consequence of
the differences in
![]() ,
but the trend is reversed closer to degeneracy. Obviously this
variation in the slope of the MLR will produce a different shape in the
peak of the LF, and in particular we expect a stronger peak
when EOS+SCH are used.
,
but the trend is reversed closer to degeneracy. Obviously this
variation in the slope of the MLR will produce a different shape in the
peak of the LF, and in particular we expect a stronger peak
when EOS+SCH are used.
Table 1:
Hydrogen burning minimum mass (HBMM) for Z=0.0002
and Z=0.0006, [![]() /Fe] = 0,
and different Y.
/Fe] = 0,
and different Y.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12516f6.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg55.png)
|
Figure 6: Comparison at very low masses between the MLR obtained using models computed with different equations of state (see text). |
| Open with DEXTER | |
An interesting theoretical feature of the models at the boundary
between low mass stars and brown dwarfs is shown in Fig. 6. This figure
refers to the Z=0.0002 case, for which an
extended atmospheric grid is available. In between the HBMM -
the smallest mass that stabilizes in MS,
in a configuration in which the total luminosity is
provided by the proton-proton (p-p) reactions in the core -
and the pure brown dwarfs - that never ignite the
p-p chain - there is a small range of masses for
which nuclear burning contributes to the stellar luminosity for even
several billion years, but in the end these objects finally cool as
brown dwarfs. This is a common occurrence in
population I (the transition masses defined in D'Antona & Mazzitelli 1985),
where the MS merges without discontinuities into the brown
dwarf cooling sequences. On the contrary, the MS of the
population II has a much sharper drop, because the much
smaller opacities put the HBMM at minimum luminosity a factor of about
ten higher, so that the transition masses cover a very small
mass range. There is then a ``luminosity gap'' between the end
of the MS and the luminosity at which the smaller brown dwarfs are able
to slow their cooling down to the typical age of population II
stars (10-12 Gyr). Figure 6 translates into
possible LF. In Fig. 7 LFs
for 10 and 13 Gyr are plotted, assuming a
power law MF with an exponent ![]() = -0.5.
At 13 Gyr, the low mass brown dwarfs should emerge as
a small peak at
= -0.5.
At 13 Gyr, the low mass brown dwarfs should emerge as
a small peak at ![]()
![]() 18,
corresponding to near infrared magnitudes of
18,
corresponding to near infrared magnitudes of ![]() 30 at the
distance of NGC 6397. The peak is
30 at the
distance of NGC 6397. The peak is ![]() 1 mag brighter if the age is
3 Gyr smaller. We regard this prediction as an educated guess
on the possibility that the dimmest luminosities regime is populated
not only by white dwarfs (Richer
et al. 2008) but also by very cool brown dwarfs.
However, dynamical models indicate that these objects should be
preferentially stripped from the cluster. Since there is a strong
difference in these two populations, as the cool white dwarfs would be
located at a color
1 mag brighter if the age is
3 Gyr smaller. We regard this prediction as an educated guess
on the possibility that the dimmest luminosities regime is populated
not only by white dwarfs (Richer
et al. 2008) but also by very cool brown dwarfs.
However, dynamical models indicate that these objects should be
preferentially stripped from the cluster. Since there is a strong
difference in these two populations, as the cool white dwarfs would be
located at a color ![]()
![]() 1-1.2 mag, while the cool brown dwarfs will not be visible in
the F606W band, as they have
1-1.2 mag, while the cool brown dwarfs will not be visible in
the F606W band, as they have ![]()
![]() 5.5-7 mag, only future observations with even more capable
telescopes should clarify the issue.
5.5-7 mag, only future observations with even more capable
telescopes should clarify the issue.
Table 2: Descriptions of the chemistry of the models calculated for this work.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12516f7.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg58.png)
|
Figure 7:
Theoretically predicted luminosity function for the models at the
age = 13 Gyr with Z=0.0002
and two different helium abundances. A power law with
the exponent |
| Open with DEXTER | |
5 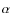 -enhanced
models, FG and SG populations, CNO enrichment
-enhanced
models, FG and SG populations, CNO enrichment
A comparison with low metallicity cluster stars requires the use of
models with ![]() -enhanced
mixtures, for which we adopt [
-enhanced
mixtures, for which we adopt [![]() /Fe] = 0.4.
As discussed only up to
/Fe] = 0.4.
As discussed only up to ![]() 30
30![]() of stars of NGC 6397 can belong to the FG, the
majority show indeed the Na-O anticorrelation, and many stars
have a very high nitrogen content. Therefore we also need models to
represent the SG. We will assume that it may differ both in
helium content and in total CNO content from the
standard FG. A resonable assumption for CNO is that
we assume an over-abundance of N by
about 1.4 dex and a variation
of -0.2 dex for O, leaving carbon unchanged
(Bragaglia, private comunication). The total ``metallicity'' Z
in the mass fraction for this CNO-enhanced mixture (CNO
of stars of NGC 6397 can belong to the FG, the
majority show indeed the Na-O anticorrelation, and many stars
have a very high nitrogen content. Therefore we also need models to
represent the SG. We will assume that it may differ both in
helium content and in total CNO content from the
standard FG. A resonable assumption for CNO is that
we assume an over-abundance of N by
about 1.4 dex and a variation
of -0.2 dex for O, leaving carbon unchanged
(Bragaglia, private comunication). The total ``metallicity'' Z
in the mass fraction for this CNO-enhanced mixture (CNO![]() )
is now Z=0.0003. We used the OPAL Web tool
to radiative opacities compute on purpose for this mixture. For T
)
is now Z=0.0003. We used the OPAL Web tool
to radiative opacities compute on purpose for this mixture. For T ![]() 15 000 K we still use the opacities by Ferguson et al. (2005),
as lower temperature opacities do not affect the structure of
the models we are considering. All models are computed for a
helium mass fraction of Y=0.24 and Y=0.28
and are summarized in Table 2.
15 000 K we still use the opacities by Ferguson et al. (2005),
as lower temperature opacities do not affect the structure of
the models we are considering. All models are computed for a
helium mass fraction of Y=0.24 and Y=0.28
and are summarized in Table 2.
In general, as discussed in the analysis by Ventura et al. (2009), the largest differences between standard and CNO-enhanced mixtures are found in the ionization zone of the CNO elements, but in this case the differences are very small since the variation is not very significant, and the initial abundances are very small. As a result, pratically no differences are found in effective temperature and luminosity of the models (see Fig. 8).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12516f8.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg59.png)
|
Figure 8: We show the comparison between the diagram of the standard CNO tracks at different masses(full line) and the ``peculiar'' ones calculated (dashed and dotted line) with the evolution of the same mass. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12516f9.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg60.png)
|
Figure 9:
Left panel: main Sequence of
NGC 6397 from Richer
et al. (2008). Also shown are the best-fit
isochrones for FG (red) and SG (green) populations. Numbers indicate
stellar masses (up-FG, down-SG) of the same models (crosses-FG, open
circle-SG) in |
| Open with DEXTER | |
Another possible hypothesis is that oxygen in the SG is
basically similar to the FG value, as most of the Carretta et al. (2009a)
measurements for O are only upper limits. In this
case, the CNO abundance becomes even larger. We accordingly
adopt as boundary conditions the
grid [M/H] = -1.5. (CNO![]()
![]() models, see
Table 2).
As reported in Fig. 8 the differences
in this case are very small as well, but for masses of about
0.3
models, see
Table 2).
As reported in Fig. 8 the differences
in this case are very small as well, but for masses of about
0.3 ![]() the temperature is a little lower.
the temperature is a little lower.
6 Comparison with the data of NGC 6397
We analyze both the CMD diagram and the luminosity function simulations.
6.1 Color-magnitude diagram
In Fig. 9
we compare the models with the deep photometry of NGC 6397 by Richer et al. (2008).
We plotted the isochrone that allows for the best fit of both the low
main sequence and the TO for the labelled value of distance modulus and
reddening, with [Fe/H] = -1.99 dex (Carretta et al. 2009c)
and [![]() /Fe] = 0.4
(solid line-red in the electronic version) and with an age of
12 Gyr, which is comparable with the age obtained from the
white dwarf cooling sequence of NGC 6397 by Hansen et al. (2007).
The distance modulus in the F814W photometric
band is compatible with the true distance modulus (=12.03 mag)
and
/Fe] = 0.4
(solid line-red in the electronic version) and with an age of
12 Gyr, which is comparable with the age obtained from the
white dwarf cooling sequence of NGC 6397 by Hansen et al. (2007).
The distance modulus in the F814W photometric
band is compatible with the true distance modulus (=12.03 mag)
and ![]() (=0.20 mag) reported in literature (see for example
Table 3 of Richer
et al. 2008).
(=0.20 mag) reported in literature (see for example
Table 3 of Richer
et al. 2008).
As already found by Richer
et al. (2008), below 0.20 ![]() the isochrone and the data do not match perfectly, but the
data appear to terminate at about the magnitude predicted by models. We
thus confirm the suggestion of Richer
et al. (2008) that they have observed the
termination of the hydrogen burning sequence.
the isochrone and the data do not match perfectly, but the
data appear to terminate at about the magnitude predicted by models. We
thus confirm the suggestion of Richer
et al. (2008) that they have observed the
termination of the hydrogen burning sequence.
In Fig. 9
we also show (dashed line-green in the electronic version) the position
of the isochrone obtained with models computed with Y=0.28
and CNO![]() using the same distance modulus and age as used for the
FG isochrone. The two isochrones are very similar except
around
using the same distance modulus and age as used for the
FG isochrone. The two isochrones are very similar except
around ![]() =
23 mag, where they deviate and the FG isochrone is a
little brighter. This aspect is important to understand if the
tightness of the MS at this interval of magnitude depends on
observational error only or is the consequence of the presence of a
second generation made of stars with higher helium abundance and
CNO enhancement. We select data within three different
intervals of half magnitude below the MS turnoff, and rectify
their colors by subtracting the color of their best-fit line,
as shown in Fig. 10,
in the left and medium panels. We do not consider the possible presence
of binaries, as Davis
et al. (2008) have shown that NGC 6397 has
a primordial binary fraction of only
=
23 mag, where they deviate and the FG isochrone is a
little brighter. This aspect is important to understand if the
tightness of the MS at this interval of magnitude depends on
observational error only or is the consequence of the presence of a
second generation made of stars with higher helium abundance and
CNO enhancement. We select data within three different
intervals of half magnitude below the MS turnoff, and rectify
their colors by subtracting the color of their best-fit line,
as shown in Fig. 10,
in the left and medium panels. We do not consider the possible presence
of binaries, as Davis
et al. (2008) have shown that NGC 6397 has
a primordial binary fraction of only ![]() 1
1![]() .
The histogram of the color displacements from the best-fit line, shown
in the right panels, is fitted with a Gaussian profile with
the labelled
.
The histogram of the color displacements from the best-fit line, shown
in the right panels, is fitted with a Gaussian profile with
the labelled
![]() .
.
In the same panel we report the color displacements for each
interval of magnitude for synthetic populations (assuming the distance
modulus for NGC 6397 reported in Fig. 9) under the
hypothesis that 30![]() of all stars are primordial (standard helium and
CNO abundance), and the remaining 70
of all stars are primordial (standard helium and
CNO abundance), and the remaining 70![]() are composed by a mixture of SG population with CNO
are composed by a mixture of SG population with CNO![]() and helium respectively up to Y =
YUP = 0.25, 0.26 and 0.28. As expected, the
largest difference between
and helium respectively up to Y =
YUP = 0.25, 0.26 and 0.28. As expected, the
largest difference between ![]() is obtained in the third interval of magnitude. From the values of
dispersion reported we obtain that a SG made of stars with
helium dispersion of
is obtained in the third interval of magnitude. From the values of
dispersion reported we obtain that a SG made of stars with
helium dispersion of ![]() is compatible with the tightness of the MS
of NGC 6397.
is compatible with the tightness of the MS
of NGC 6397.
In the case of the CNO![]()
![]() models (see Sect. 5) the isochrone calculated for Y=0.28
overlaps exactly on the FG's. In this case the observational
spread of MS at low magnitude may suggest an even broader spread of
helium between FG and SG.
models (see Sect. 5) the isochrone calculated for Y=0.28
overlaps exactly on the FG's. In this case the observational
spread of MS at low magnitude may suggest an even broader spread of
helium between FG and SG.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12516f10.ps}\vspace*{5mm}
\i...
...6f11.ps}\vspace*{5mm}
\includegraphics[width=9cm,clip]{12516f12.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg64.png)
|
Figure 10:
a) In each row a small portion of the MS of
NGC 6397 is shown on the far left, while in the
middle panel the magnitude
|
| Open with DEXTER | |
6.2 Luminosity function
We now compare the observed luminosity function with the theoretical simulations. We use the magnitudes in the F814W filter and derive synthetic populations from models at different ages, in the plausible range from 9 to 14 Gyr.
The mass-luminosity relation from our models was discussed in
Sect. 4.1; now we discuss the choice of the mass
function (MF). We consider this cluster initially as formed by
unique population to define a method to compare the theoretical and
observational luminosity function. Due to the dynamical evolution of
the cluster, the present MF is not the initial one.
NGC 6397 has a collapsed core (Djorgovski
& King 1986), as it has evolved past the
potentially catastrophic phase of core collapse, and is dynamically
old. In particular it has been shown that NGC 6397
exhibits mass segregation, which certainly has affected the MF (Hurley et al. 2008). Silvestri et al. (1998)
have shown, adopting their own low mass models and those by Baraffe et al. (1997),
that the bulk of the MF can be described by a unique power law
of the form ![]()
![]() with index
with index ![]() = -0.5.
Richer et al. (2008)
found that
= -0.5.
Richer et al. (2008)
found that ![]() = -0.13
gives the highest
= -0.13
gives the highest ![]() when comparing the models with their data of NGC 6397. They
found an even better result when a lognormal distribution is used,
which has the advantage to truncate the LF at the extreme low mass end,
but the disadvantage to introduce a new parameter. A similar
result was obtained by De Marchi
et al. (2000) who suggested that no single
power law distribution is compatible with the MS of
NGC 6397; in particular they found that the MF is
less steep for M
when comparing the models with their data of NGC 6397. They
found an even better result when a lognormal distribution is used,
which has the advantage to truncate the LF at the extreme low mass end,
but the disadvantage to introduce a new parameter. A similar
result was obtained by De Marchi
et al. (2000) who suggested that no single
power law distribution is compatible with the MS of
NGC 6397; in particular they found that the MF is
less steep for M ![]() 0.3
0.3 ![]() .
.
We simulate the synthetic populations using a
power law MF with two different slopes above (![]() )
and below (
)
and below (![]() )
a cutoff magnitude of the range of
)
a cutoff magnitude of the range of ![]() =
8.5-10.5 mag (here we consider a single MF
as a particular case with
=
8.5-10.5 mag (here we consider a single MF
as a particular case with ![]() =
= ![]() ); this
cutoff magnitude corresponds to a ``cutoff mass'' for a chosen
distance modulus At a fixed age, MLR gives the magnitudes of each
extracted mass according to the chosen MF, which depends on four
parameters (
); this
cutoff magnitude corresponds to a ``cutoff mass'' for a chosen
distance modulus At a fixed age, MLR gives the magnitudes of each
extracted mass according to the chosen MF, which depends on four
parameters (![]() ,
,
![]() ,
,
![]() and distance). We simulate photometric errors considering gaussian
errors for the magnitudes of each extracted mass to reproduce the width
of the upper main sequence. In addition we have taken into
consideration the uncertainties in completeness by multiplying the
random extractions in a given interval of masses for the completeness
fractions given in Table 4 of Richer
et al. (2008) which determined with the artificial
star test described in Anderson
et al. (2008).
and distance). We simulate photometric errors considering gaussian
errors for the magnitudes of each extracted mass to reproduce the width
of the upper main sequence. In addition we have taken into
consideration the uncertainties in completeness by multiplying the
random extractions in a given interval of masses for the completeness
fractions given in Table 4 of Richer
et al. (2008) which determined with the artificial
star test described in Anderson
et al. (2008).
We have then used the Kolmogorov-Smirnov test to compare the
observed luminosity function of NGC 6397 with the theoretical
one, which depends on the MF used to extract masses (![]() ,
,
![]()
![]() ),
as well as on the age and distance modulus. This statistical
method has the advantage of being non-parametric, and without making
assumptions about the distribution function of the data,
it returns the probability that two arrays of data values are
drawn from the same distribution. The scalar KS
),
as well as on the age and distance modulus. This statistical
method has the advantage of being non-parametric, and without making
assumptions about the distribution function of the data,
it returns the probability that two arrays of data values are
drawn from the same distribution. The scalar KS![]() (varying
between 0 and 1) gives the significance level of the
KS statistic, i.e. the probability with which we can
accept the null hypothesis. KS = 1 means
that the simulated and observed data follow the same function.
(varying
between 0 and 1) gives the significance level of the
KS statistic, i.e. the probability with which we can
accept the null hypothesis. KS = 1 means
that the simulated and observed data follow the same function.
![\begin{figure}
\par\includegraphics[width=7.15cm,clip]{12516f13.ps}\vspace*{5mm}...
...4.ps}\vspace*{5mm}
\includegraphics[width=7.15cm,clip]{12516f15.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg68.png)
|
Figure 11:
Distribution of KS with distance modulus for the labelled value of Z
and Y and for different
|
| Open with DEXTER | |
Another great advantage of this statistical method is that the two
arrays of data do not need to have the same number of elements; this
means that we can build our synthetic populations with a greater number
of stars then the actual number of stars from which we derived the
observed LF, making the results independent from the random extraction.
We have studied the dependence of KS numbers as a function of
distance modulus for each of the four free parameters (age, ![]() ,
,
![]() and
and
![]() )
used to build the synthetic population, and then we have compared the
results to choose the best fit parameter. In particular as
done by Richer et al.
(2008) for their
)
used to build the synthetic population, and then we have compared the
results to choose the best fit parameter. In particular as
done by Richer et al.
(2008) for their ![]() method both
method both ![]() and
and ![]() were allowed to range from -1 and 1 in
200 steps. We have explored the case of a single MF
as a special case in point (
were allowed to range from -1 and 1 in
200 steps. We have explored the case of a single MF
as a special case in point (![]() =
= ![]() ). We find
that the best combination of power law exponents for higher
and lower masses, respectively, are
). We find
that the best combination of power law exponents for higher
and lower masses, respectively, are ![]() = -0.7 and
= -0.7 and ![]() = -0.1.
The upper panel of Fig. 11,
where the variation of KS are shown with the distance modulus
for various selected
= -0.1.
The upper panel of Fig. 11,
where the variation of KS are shown with the distance modulus
for various selected ![]() ,
justifies our choice. We also note that the distance modulus for which
we have the higher probability is about the same distance modulus for
which we have the best comparison between isochrones and CMD
(see Fig. 9),
which further confirms the validity of our method. The same result is
obtained using models with higher helium abundance. For these values we
also report in Fig. 11
KS as a function of distance modulus for different ages (medium panel)
and for different cutoff magnitudes (lower panel). In the bottom panel
the case of a single power law with an index of -0.7
is also shown (black triangles): we see that a unique
power law does not give a good match to the
observed LF. Notice however that for higher masses this value
is very different from the one obtained by Richer
et al. (2008) (=-0.13). Still we wish to stress that
our result is consistent with their consideration that a lognormal
function produces better
,
justifies our choice. We also note that the distance modulus for which
we have the higher probability is about the same distance modulus for
which we have the best comparison between isochrones and CMD
(see Fig. 9),
which further confirms the validity of our method. The same result is
obtained using models with higher helium abundance. For these values we
also report in Fig. 11
KS as a function of distance modulus for different ages (medium panel)
and for different cutoff magnitudes (lower panel). In the bottom panel
the case of a single power law with an index of -0.7
is also shown (black triangles): we see that a unique
power law does not give a good match to the
observed LF. Notice however that for higher masses this value
is very different from the one obtained by Richer
et al. (2008) (=-0.13). Still we wish to stress that
our result is consistent with their consideration that a lognormal
function produces better ![]() values
than the best fitting single power law MF.
In fact, when a lognormal function is used one has two
adjustable parameters, as in our case. Concerning the age, as shown in
the medium panel of Fig. 11,
the best agreement with observations is obtained for an age of
14-13 Gyr, but if we also consider the best distance
moduli and take into account the CMD we can choose 12 Gyr
together with
values
than the best fitting single power law MF.
In fact, when a lognormal function is used one has two
adjustable parameters, as in our case. Concerning the age, as shown in
the medium panel of Fig. 11,
the best agreement with observations is obtained for an age of
14-13 Gyr, but if we also consider the best distance
moduli and take into account the CMD we can choose 12 Gyr
together with ![]() =
9.5 mag, corresponding to M
=
9.5 mag, corresponding to M ![]() 0.18
0.18 ![]()
![]() .
.
In Fig. 12
we report the NGC 6397 MS LF compared with the best fitting
double power law mass functions. The overall agreement is
satisfactory. Only at ![]()
![]() 12 mag (
12 mag (![]()
![]() ), are the observed
stars fewer then predicted; this could mean that the MF is even flatter
at these lowest masses due to more effective evaporation,
but it may also be due to some deficiency in the models. In
Fig. 13
we also show the distribution of KS in the case that 30
), are the observed
stars fewer then predicted; this could mean that the MF is even flatter
at these lowest masses due to more effective evaporation,
but it may also be due to some deficiency in the models. In
Fig. 13
we also show the distribution of KS in the case that 30![]() of the stars belong to FG (Y=0.24
and CNOx1a) and 70
of the stars belong to FG (Y=0.24
and CNOx1a) and 70![]() to the SG (YUP = 0.26 and CNO
to the SG (YUP = 0.26 and CNO![]() ), which gives the best match
of the width of the MS (see Fig. 10) and in the case
where all stars belong to SG. The conclusion is that as
comparable KS and reliable distance moduli are obtained in all cases,
that is from the width of the MS as well as from the luminosity
function, we cannot exclude that the cluster contains either a mixture
of stars with different helium, or a single helium abundance
for all stars.
), which gives the best match
of the width of the MS (see Fig. 10) and in the case
where all stars belong to SG. The conclusion is that as
comparable KS and reliable distance moduli are obtained in all cases,
that is from the width of the MS as well as from the luminosity
function, we cannot exclude that the cluster contains either a mixture
of stars with different helium, or a single helium abundance
for all stars.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12516f16.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg71.png)
|
Figure 12: Comparison between observed and calculated distribution of MS stars of NGC 6397 for the labelled values of the parameters. The power law used is the same as the one of Fig. 11. The error bars take into account the Poisson's error and incompleteness corrections. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12516f17.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg72.png)
|
Figure 13: Distribution of KS with distance modulus for different synthetic populations. |
| Open with DEXTER | |
7 Conclusions
We have computed new models for the main sequence down to the hydrogen
burning minimum mass, adopting two different versions of an updated
equation of state and made simulations of the luminosity functions for
different choices of the mass function and the initial helium content.
The results are compared with the recent observations of the MS of
NGC 6397 by Richer
et al. (2008). Using a Kolmogorov-Smirnov test to
compare observed and simulated LF we found that a double
power law for the mass function reproduces the observed
luminosity function well in the F814W photometric
band. However, both the models for a simple or a mixed population
according the spectroscopic data provide a good fit of LF.
A stronger result is obtained from the analysis of the width
of MS from which we find that in any case any helium
variations must be confined within ![]() = 0.02 in
the case of CNO overabundance predicted by a mixing
between 50
= 0.02 in
the case of CNO overabundance predicted by a mixing
between 50![]() of pristine gas and 50
of pristine gas and 50![]() of gas ejected by 5
of gas ejected by 5 ![]() AGB stars as suggested by Ventura
& D'Antona (2009). Instead we find that a broader
spread (0.02
AGB stars as suggested by Ventura
& D'Antona (2009). Instead we find that a broader
spread (0.02 ![]()
![]()
![]() 0.04)
in helium between the primordial and intermediate generation is
compatible with the width of the main sequence when CNO
0.04)
in helium between the primordial and intermediate generation is
compatible with the width of the main sequence when CNO![]()
![]() models
are considered.
models
are considered.
The complete sets of isochrones transformed for the ACS filters F814W and F606W, calculated for this work, are available upon request to the authors and will be soon inserted in site http://www.mporzio.astro.it/%7Etsa/
AcknowledgementsWe thank S. Cassisi for providing the color-transformations and J. Anderson, A. Bragaglia, A. Dotter, A. Milone and H. Richer and G. De Marchi for useful discussions. Financial support for this study was provided by MIUR under the PRIN project ``Asteroseismology: a necessary tool for the advancement in the study of stellar structure, dynamics and evolution'', P.I. L. Paternó and by the PRIN MIUR 2007 ``Multiple stellar populations in globular clusters: census, characterization and origin''.
References
- Anderson, J., King, I., Richer, H. B., et al. 2008, AJ, 125, 2114 [Google Scholar]
- Alexander, D. R., Brocato, E., Cassisi, S., et al. 1997, A&Am, 317, 90 [NASA ADS] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, NuPhA., 656, 3A [NASA ADS] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1997, A&A, 327, 1054 [NASA ADS] [Google Scholar]
- Bedin, L. R., Cassisi, S., Castelli, F., et al. 2005, MNRAS, 357, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Bessel, M. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., Pasquini, L., Spite, F., et al. 2002, A&A, 390, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caloi, V., & D'Antona, F. 2005, A&A, 121, 95 [Google Scholar]
- Canuto, V. M., & Mazzitelli, I. 1991, AJ, 370, 295 [Google Scholar]
- Canuto, V. M., Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Castellani, V., Ciarcelluti, P., Piotto, G., & Zoccali, M. 2000, MNRAS, 315, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094C [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., & Cacciari, C. 2004, ApJ, 610, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Gratton, R. G., Lucatello, S., Bragaglia, A., & Bonifacio, P. 2005, A&A, 433, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2006, A&A, 450, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009a, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., & Lucatello, S. 2009b, A&A, 505, 539 [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., D'Orazi, V., & Lucatello, S. 2009c, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, ed. N. Piskunov et al., IAU Symp. 210, A20 [arXiv:astro-ph/0405087] [Google Scholar]
- Catelan, M., Borissova, J., Sweigart, A. V., & Spassova, N. 1998, ApJ, 494, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Coc, A., Vangioni-Flam, E., Descouvemont, P., Adahchour, A., & Angulo, C. 2004, ApJ, 600, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Copeland, H., Jensen, J. O., & Jorgensen, H. 1970, A&A, 5, 12 [NASA ADS] [Google Scholar]
- Chabrier, G., & Baraffe, I. 1997, A&A, 1997 [Google Scholar]
- Davis, D. S., Richer, H. B., Anderson, J., et al. 2008, AJ, 135, 2155D [NASA ADS] [CrossRef] [Google Scholar]
- D'Antona, F. 1987, ApJ, 320, 653 [NASA ADS] [CrossRef] [Google Scholar]
- D'Antona, F. 1998, The Stellar Initial Mass Function, 38th Herstmonceux Conference, 142, 157 [Google Scholar]
- D'Antona, F., & Caloi, V. 2004, 611, 871 [Google Scholar]
- D'Antona, F., & Caloi, V. 2008, MNRAS, 390, 693 [NASA ADS] [CrossRef] [Google Scholar]
- D'Antona, F., & Mazzitelli, I. 1985, ApJ, 296, 502D [Google Scholar]
- D'Antona, F., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007a, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Marchi, G., Paresce, F., & Pulone, L. 2000, ApJ, 530, 342 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Pols, O. R., Langer, N. & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D'Ercole, A., Vesperini, E., D'Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Di Criscienzo, M., Ventura, P., & D'Antona, F. 2009, A&A, 496, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Djorgovski, S., & King, I. R. 1986, ApJ, 305, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A. 2007, Ph.D. Thesis [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremovic, D., et al. 2007, AJ, 134, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Graboske, H. C., Jr., & van Horn, H. M. 1977, ApJS, 35, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Bragaglia, A., Carretta, E., et al. 2003, A&A, 408, 529G [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1999, A&A, 347, 348G [NASA ADS] [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Heiter, U., Kupka, F., van't Veer-Menneret, C., et al. 2002, A&A, 392, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, B., Anderson, J., Brewer, J., et al. 2007, ApJ, 671, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, R. J., Shara, M. M., Richer, H. B., et al. 2008, AJ, 135, 2129 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., & Bolte, M. 1998, AJ, 115, 693 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. R., Anderson, J., Cool, A. M., & Piotto, G. 1998, ApJ, 492, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Korn, A. J., Grundahl, F., Richard, O., et al. 2007, ApJ, 671, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y.-W., Demarque, P., & Zinn, R. 1994, ApJ, 423, 248 [Google Scholar]
- Lind, K., Primas, F., Charbonnel, C., Grundahl, F., & Asplund, M. 2009, A&A, 503, 545L [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Magni, G., & Mazzitelli, I. 1979, A&A, 72, 134 [NASA ADS] [Google Scholar]
- Milone, A. P., Bedin, L. R., Piotto, G., et al. 2008, ApJ, 673, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Montalban, J., D'Antona, F., & Mazzitelli, I. 2000, A&A, 360, 935 [NASA ADS] [Google Scholar]
- Montalbán, J., Kupka, F., D'Antona, F., & Schmidt, W. 2001, A&A, 370, 982 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montalbán, J., D'Antona, F., Kupka, F., & Heiter, U. 2004, A&A, 416, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paresce, F., De Marchi, G., & Romaniello, M. 1995, ApJ, 440, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Ecuvillon, A., Bonifacio, P., & Wolff, B. 2008, A&A, 489, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piotto, G., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., Baiko, D. A., Haensel, P., & Yakovlev, D. G. 1999, A&A, 346, 345P [NASA ADS] [Google Scholar]
- Pumo, M. L., D'Antona, F., & Ventura, P. 2008, ApJ, 672, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, S. V., & Cohen, J. G. 2002, AJ, 123, 3277 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Rey, S. C., Yoon, S. J., Lee, Y. W., Chaboyer, B., & Sarajedini, A. 2001, AJ, 122, 3219 [NASA ADS] [CrossRef] [Google Scholar]
- Richer, H. B., Anderson, J., Brewer, J., et al. 2006, Science, 313, 936 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Richer, H. B., Dotter, A., Hurley, J., et al. 2008, AJ, 135, 2141 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Silvestri, F., Ventura, P., D'Antona, F., & Mazzitelli, I. 1998, A&A, 334, 953 [NASA ADS] [Google Scholar]
- Sirianni, M., et al. 2005, PASP, 117, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Stolzmann W., & Blöcker, T. 2000, A&A, 361, 1152 [NASA ADS] [Google Scholar]
- Vandenberg, D. A., & Clem, J. L. 2003, AJ, 126, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., & D'Antona, F. 2009, A&A, 499, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., D'Antona, F., & Mazzitelli, I. 2007, Ap&SS, 420 [Google Scholar]
- Ventura, P., Caloi, V., D'Antona, F., et al. 2009, MNRAS, 399, 934 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... class
![[*]](/icons/foot_motif.png)
- We do not wish to include
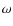 Cen among the
classic GCs, as it also shows large metallicity variations,
indicating that its evolution is partially similar to that of a
massive GC, containing e.g. a population with a very high
helium content, but also closer to that of a small galaxy,
as the supernova ejecta take part in the star formation
events.
Cen among the
classic GCs, as it also shows large metallicity variations,
indicating that its evolution is partially similar to that of a
massive GC, containing e.g. a population with a very high
helium content, but also closer to that of a small galaxy,
as the supernova ejecta take part in the star formation
events.
- ... ``primordial''
![[*]](/icons/foot_motif.png)
- Indeed, while Carretta
et al. (2009a) have only four ``primordial'' stars
in their sample of O-Na measurements for this cluster, they
have determined Na abundances in a larger number of stars, and
also in this larger sample sodium is ``normal'', that is
similar to the sodium of the halo stars that have a similar
metallicity, in
 25-30
25-30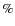 of stars.
of stars.
- ... (2004)
![[*]](/icons/foot_motif.png)
- Technical Report http://freeeos.sourceforge.net/
- ... (2004)
![[*]](/icons/foot_motif.png)
- http://freeeos.sourceforge.net/
- ... atmosphere
![[*]](/icons/foot_motif.png)
- The same approach has been adopted for pre-main sequence stars in Di Criscienzo et al. (2009).
- ... 2.0
![[*]](/icons/foot_motif.png)
- The choice of the
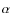 parameter is less
and less critical when decreasing the mass, as the external layers
become so dense that convection becomes more and more adiabatic.
Nevertheless, we use
parameter is less
and less critical when decreasing the mass, as the external layers
become so dense that convection becomes more and more adiabatic.
Nevertheless, we use 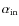 =
2.0 to allow for a smooth
=
2.0 to allow for a smooth 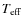 transition
between the upper (M
transition
between the upper (M 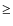 0.5
0.5 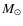 )
and lower (M
)
and lower (M 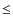 0.5
0.5 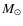 )
MS models.
)
MS models.
- ... scalar KS
![[*]](/icons/foot_motif.png)
- We use the kstwo algorithm from ``Numerical Recipes'', 3nd edn.
- ...
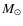
![[*]](/icons/foot_motif.png)
- This value is much lower then the mass (
 0.3
0.3 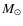 )
found by De Marchi
et al. (2000).
)
found by De Marchi
et al. (2000).
All Tables
Table 1:
Hydrogen burning minimum mass (HBMM) for Z=0.0002
and Z=0.0006, [![]() /Fe] = 0,
and different Y.
/Fe] = 0,
and different Y.
Table 2: Descriptions of the chemistry of the models calculated for this work.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12516f1.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg32.png)
|
Figure 1:
We show the region of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12516f2.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg33.png)
|
Figure 2:
Adiabatic gradient (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12516f3.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg37.png)
|
Figure 3: HR diagram location at 10 Gyr for models with Z=0.0006, the labelled masses are calculated with different EOS tables. Models from the Dartmouth Stellar Evolution Database (full dots) and from Baraffe et al. (1997) (asterisks), with the same metallicity as ours, are also shown for comparison. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12516f4.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg49.png)
|
Figure 4: Evolutionary tracks, starting from the pre-main-sequence, for three different masses with Z=0.0006 and the different value of initial helium.The filled circle labels the position in the HR diagram of the star at age = 10 Gyr. Only for the highest mass the tracks with the all three Y are shown. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12516f5.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg50.png)
|
Figure 5: The MLR for models at 10 Gyr having the labelled value of metallicity and different helium abundance (=0.24-open circles, =0.28-filled triangles, =0.32-filled circles, =0.40-asterisks). In each case the lower masses are the derived HBMM and reported in Table 1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12516f6.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg55.png)
|
Figure 6: Comparison at very low masses between the MLR obtained using models computed with different equations of state (see text). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12516f7.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg58.png)
|
Figure 7:
Theoretically predicted luminosity function for the models at the
age = 13 Gyr with Z=0.0002
and two different helium abundances. A power law with
the exponent |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{12516f8.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg59.png)
|
Figure 8: We show the comparison between the diagram of the standard CNO tracks at different masses(full line) and the ``peculiar'' ones calculated (dashed and dotted line) with the evolution of the same mass. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{12516f9.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg60.png)
|
Figure 9:
Left panel: main Sequence of
NGC 6397 from Richer
et al. (2008). Also shown are the best-fit
isochrones for FG (red) and SG (green) populations. Numbers indicate
stellar masses (up-FG, down-SG) of the same models (crosses-FG, open
circle-SG) in |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12516f10.ps}\vspace*{5mm}
\i...
...6f11.ps}\vspace*{5mm}
\includegraphics[width=9cm,clip]{12516f12.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg64.png)
|
Figure 10:
a) In each row a small portion of the MS of
NGC 6397 is shown on the far left, while in the
middle panel the magnitude
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.15cm,clip]{12516f13.ps}\vspace*{5mm}...
...4.ps}\vspace*{5mm}
\includegraphics[width=7.15cm,clip]{12516f15.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg68.png)
|
Figure 11:
Distribution of KS with distance modulus for the labelled value of Z
and Y and for different
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12516f16.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg71.png)
|
Figure 12: Comparison between observed and calculated distribution of MS stars of NGC 6397 for the labelled values of the parameters. The power law used is the same as the one of Fig. 11. The error bars take into account the Poisson's error and incompleteness corrections. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12516f17.ps}
\end{figure}](/articles/aa/full_html/2010/03/aa12516-09/Timg72.png)
|
Figure 13: Distribution of KS with distance modulus for different synthetic populations. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


