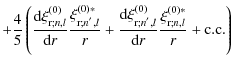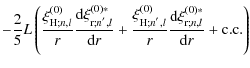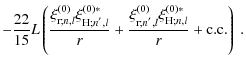| Issue |
A&A
Volume 508, Number 1, December II 2009
|
|
|---|---|---|
| Page(s) | 345 - 353 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/200912284 | |
| Published online | 08 October 2009 | |
A&A 508, 345-353 (2009)
Mode excitation by turbulent convection in rotating stars
I. Effect of uniform rotation
K. Belkacem1,2 - S. Mathis3 - M. J. Goupil2 - R. Samadi2
1 - Institut d'Astrophysique et Géophysique, Université de Liège, Allée du 6 Août 17, 4000 Liège, Belgium
2 -
Observatoire de Paris, LESIA, CNRS UMR 8109, 92195 Meudon, France
3 -
CEA/DSM/IRFU/Service d'Astrophysique, CE Saclay, 91191 Gif-sur-Yvette, France
Received 6 April 2009 / Accepted 9 September 2009
Abstract
We focus on the influence of the Coriolis acceleration
on the stochastic excitation of oscillation modes in convective regions of rotating stars.
Our aim is to estimate the asymmetry between excitation rates of prograde and retrograde modes.
We extend the formalism
derived for obtaining stellar p- and g-mode amplitudes (Samadi & Goupil 2001, A&A, 370, 136; Belkacem et al. 2008, A&A, 478, 163)
to include the effect of the Coriolis acceleration.
We then study the special case of uniform rotation
for slowly rotating stars by performing a perturbative analysis.
This allows us to consider the cases of the Sun and the CoRoT target HD 49933.
We find that, in the subsonic regime,
the influence of rotation as a direct contribution to mode driving
is negligible compared to the Reynolds stress contribution.
In slow rotators, the indirect effect of the modification of
the eigenfunctions on mode excitation is investigated by performing
a perturbative analysis of the excitation rates.
The excitation of solar p modes is found to be affected by rotation
with excitation-rate asymmetries between prograde and retrograde modes of the order of several percent.
Solar low-order g modes are also affected by uniform rotation and
their excitation-rate asymmetries are found to reach 10%.
The CoRoT target HD 49933 is rotating more rapidly than the Sun (
![]() ),
and we show that the resulting excitation-rate asymmetry is about 10% for the excitation rates of p modes.
We demonstrate that p and g mode excitation rates
are modified by uniform rotation through the Coriolis acceleration.
A study of the effect of differential rotation will be presented in a forthcoming paper.
),
and we show that the resulting excitation-rate asymmetry is about 10% for the excitation rates of p modes.
We demonstrate that p and g mode excitation rates
are modified by uniform rotation through the Coriolis acceleration.
A study of the effect of differential rotation will be presented in a forthcoming paper.
Key words: convection - turbulence - stars: oscillations
1 Introduction
Internal dynamical processes in stars and wave excitation, propagation, and induced transport can be strongly influenced by rotation. Those mechanisms modify stellar internal structure and evolution with significant consequences for example for galactic evolution (Maeder 2009). The impact of rotation on stars is now studied by including models of internal transport processes in stellar evolutionary codes (see for instance Maeder 2009; Decressin et al. 2009; Talon et al. 1997; Maeder & Meynet 2000; Espinosa Lara & Rieutord 2007, and references therein). Asteroseismology is also being increasingly developed with results from the CoRoT (Appourchaux et al. 2008; Michel et al. 2008a,b) and KEPLER (Christensen-Dalsgaard et al. 2008) missions, which place constraints on stellar modeling. Those spatial missions allow us to study stars that are slow as well as very rapid rotators.
Since the pioneering works of Ulrich (1970) and Leibacher & Stein (1971), which led to the identification of the solar five-minute oscillations as global acoustic standing waves (p modes), the Sun internal structure has been determined from the knowledge of its oscillation frequencies. One of the remaining key issues is the detection and identification of gravity modes (Appourchaux et al. 2000; García et al. 2007; Gabriel et al. 2002; García et al. 2008a; Turck-Chièze et al. 2004; Mathur et al. 2007) for determining the rotation profile in the nuclear region (García et al. 2008b; Mathur et al. 2008). Oscillation modes are indeed crucial for probing the interior of rotating stars.
Stochastic excitation of radial modes by turbulent convection has been investigated by means of several approaches (Goldreich et al. 1994; Samadi & Goupil 2001; Chaplin et al. 2005; Balmforth 1992; Goldreich & Keeley 1977). These methods differ from each other in the nature of the assumed excitation sources, the adopted simplifications and approximations, and by the way that the turbulent convection is described (see reviews by Stein et al. 2004; Houdek 2006). Two major mechanisms have nevertheless been identified as driving the resonant p modes of the stellar cavity: the first is related to the Reynolds stress tensor and, as such, represents a mechanical source of excitation; the second is caused by the advection of turbulent fluctuations of entropy by turbulent motions, and as such represents a thermal source of excitation (Samadi & Goupil 2001; Goldreich & Keeley 1977). Samadi & Goupil (2001) proposed a generalized formalism, taking the Reynolds and entropy fluctuation source terms into account. The satisfying agreement between modeling and observational data for the Sun (Belkacem et al. 2006b,a) permitted us to go a step further and investigate the excitation of non-radial modes in the non-rotating case (Belkacem et al. 2009,2008) and now the effect of rotation.
Our motivation is to investigate the effect of rotation on the mode excitation rates rather than the frequencies.
We then focus on the excitation rates of stochastically excited modes for which several issues can be addressed. For example,
is the excitation rate of a non-axisymmetric mode (![]() )
the same as for an axisymmetric one (m=0)?
Are prograde and retrograde modes excited in the same manner and what
are the consequences?
We pay attention to the Coriolis acceleration effects in stars,
neglecting the centrifugal acceleration-induced effects such as star
deformation.
Our first objective is to determine whether or not uniform rotation can
drive the mode efficiently, and our second is to evaluate the
excitation-rate asymmetry between prograde and retrograde modes induced
by the perturbation of the eigenfunctions by uniform rotation. The
effect of differential rotation on the mode excitation rates will be
addressed in a forthcoming paper.
)
the same as for an axisymmetric one (m=0)?
Are prograde and retrograde modes excited in the same manner and what
are the consequences?
We pay attention to the Coriolis acceleration effects in stars,
neglecting the centrifugal acceleration-induced effects such as star
deformation.
Our first objective is to determine whether or not uniform rotation can
drive the mode efficiently, and our second is to evaluate the
excitation-rate asymmetry between prograde and retrograde modes induced
by the perturbation of the eigenfunctions by uniform rotation. The
effect of differential rotation on the mode excitation rates will be
addressed in a forthcoming paper.
The paper is organized as follows. Section 2 introduces the general formalism, and a detailed derivation of the Reynolds, entropy, and rotation-induced source terms is provided. In Sect. 3, the formalism is applied to solar spheroidal modes. The special case of slow rotators, the Sun, and the CoRoT target HD 49933 are then investigated, and the results are discussed. Some conclusions are presented in Sect. 4.
2 Turbulent stochastic excitation
2.1 The inhomogeneous wave equation
We derive the inhomogeneous wave equation by taking into account
the Coriolis acceleration and differential rotation.
The fluid velocity field (![]() )
is divided into the terms
)
is divided into the terms
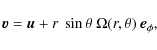
|
(1) |
where
The equation of mass conservation and motion
in the presence of axisymmetric rotation, can be written as follows (e.g., Unno et al. 1989):
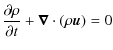
|
(2) | ||
![$\displaystyle \frac {\partial \left(\rho \vec u\right) } {\partial t} + \vec \n...
...vec u
+ r \sin \theta ~ \vec u \cdot ~ \vec \nabla \Omega ~ \vec e_\phi \right]$](/articles/aa/full_html/2009/46/aa12284-09/img18.png)
|
|||
| (3) |
where
To go further, all physical quantities are divided into an equilibrium one and a
perturbation. The subscripts 1 and 0 denote Eulerian perturbations and
equilibrium quantities, respectively, except for velocity where the subscript
1 has been dropped for ease of notation. In the following, the
velocity field ![]() is divided into two contributions, namely the
oscillation velocity (
is divided into two contributions, namely the
oscillation velocity (
![]() )
and the turbulent velocity field
(
)
and the turbulent velocity field
(
![]() ), such
that
), such
that
![]() .
Then, taking the temporal derivative of the equation of motion and using the
mass conservation equation, one then obtains
.
Then, taking the temporal derivative of the equation of motion and using the
mass conservation equation, one then obtains
where
![$\displaystyle \vec L_\Omega = \vec \nabla \left[ \alpha_s \vec v_{\rm osc} ~ \c...
...c} \right) \right]
- \vec g \nabla \cdot \left( \rho_0 \vec v_{\rm osc} \right)$](/articles/aa/full_html/2009/46/aa12284-09/img29.png)
|
|||
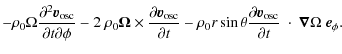
|
(5) |
The operator
| |
= | ||
| (6) |
Finally, the
and
where
2.2 Mean square amplitude for uniform rotation
Using Eq. (4), the next step is to determine the mean square amplitude of
![]() .
The procedure is the same as described in Belkacem et al. (2008).
The wave velocity field is related to the displacement by means of the relation (Unno et al. 1989)
.
The procedure is the same as described in Belkacem et al. (2008).
The wave velocity field is related to the displacement by means of the relation (Unno et al. 1989)
where
where
where
The power (P) injected into each mode with given (![]() )
is then related to the mean-squared
amplitude (
)
is then related to the mean-squared
amplitude (
![]() )
by
)
by
where the operator
Following Samadi & Goupil (2001) and Belkacem et al. (2008),
one then obtains the mean square amplitude for each mode as
where
2.3 Reynolds stress contribution
Following the formalism of Belkacem et al. (2008), we develop the turbulent
Reynolds contribution (see Appendix A for a detailed derivation),
which becomes for a given (![]() )
)
and
where
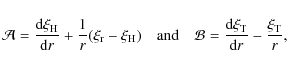
|
(17) |
and
![\begin{displaymath}{\cal F}_{\ell,\vert m\vert} = \frac{\vert m\vert (2 \ell + 1)}{2} \left[ \ell(\ell+1) - (m^2 + 1 )\right]
\end{displaymath}](/articles/aa/full_html/2009/46/aa12284-09/img76.png)
|
(18) |
and
where
Note that in absence of rotation (i.e., ![]() ),
the toroidal component of the eigenfunction
),
the toroidal component of the eigenfunction
![]() vanishes
in Eq. (12) and for
vanishes
in Eq. (12) and for
![]() and R(r) we recover the expressions given by Eqs. (22) and (23) of Belkacem et al. (2008).
From Eq. (16),
additional terms are found to appear through the toroidal component of
the eigenfunction. All are found to be positive regardless of
and R(r) we recover the expressions given by Eqs. (22) and (23) of Belkacem et al. (2008).
From Eq. (16),
additional terms are found to appear through the toroidal component of
the eigenfunction. All are found to be positive regardless of ![]() and m, implying an increase in the excitation rates.
and m, implying an increase in the excitation rates.
We emphasize that rotation is understood to create anisotropies in the Reynolds stress tensor, then off-diagonal terms (e.g., Kumar et al. 1995; Miesch 2005). An adapted spectral description of turbulent convection including the effect of rotation is thus required to compute Eq. (19) and is beyong the scope or our study.
2.4 Entropy fluctuation contribution
As shown by Samadi & Goupil (2001) and Belkacem et al. (2006b), the Reynolds stress contribution is not the unique source of excitation but one has to account for the excitation by the entropy contribution to reproduce the excitation rates for solar radial p modes.
Following Belkacem et al. (2008), the entropy source term
depends on the mode compressibility that can be estimated as
where
Hence, from Eqs. (12) and (20) the divergence of the toroidal component, which is the curl of the spherical harmonic, vanishes.
Consequently, one obtains the same result as for taking only the poloidal contribution into account.
The final expression for the contribution of entropy fluctuations remains the same as in
Belkacem et al. (2008), i.e.,
where
where
In contrast to the Reynolds contribution expression Eq. (16), the entropy one is not directly modified by rotation. Nevertheless, this contribution can be influenced indirectly by means of the modification of the radial and horizontal components of the eigenfunctions (
2.5 Rotational contributions
The rotational contributions in the inhomogeneous equation (Eqs. (4) and (8)) are
- the contribution related to the Coriolis acceleration
where we neglect the time variations in the angular velocity on a dynamical time scale. - the contribution related to the Doppler shift
- the contribution related to the differential rotation
Eventually, one obtains (see Eq. (15), Eq. (21), and Eqs. (26) to (27))
| |
= | 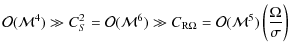
|
|
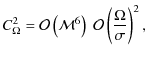
|
(29) |
where
2.6 Final balance
We have shown in Sects. 2.3 to 2.5 that in the presence of uniform rotation, the Reynolds term contribution (Eq. (15)) remains the most dominant in the subsonic regime. It can be influenced by uniform rotation in three ways;
- the turbulent velocity field can be modified by the Coriolis acceleration, hence affecting the Reynolds contribution in Eq. (15) by the source term (Eq. (19));
- the toroidal component of the eigenfunction introduces additional terms in Eq. (16);
- eventually, the poloidal components of the eigenfunctions are modified by the Coriolis acceleration and will influence the Reynolds contribution in terms of Eq. (15).
3 Application to spheroidal modes of slow rotators
As mentioned in Sect. 2.6, the velocity field can be modified by the Coriolis acceleration. However, for slow rotators the rotation rate does not significantly affect the turbulent field in the upper convective region where modes are excited, provided that the ratio of the convective frequency to the rotation rate is higher than unity. For the Sun, this requirement is fulfilled in the entire convective region except in the deepest layers, near the interface with the radiative region. Nevertheless, the contribution of these deep layers do not contribute significantly to the excitation rates for the modes considered here, i.e., low-order g modes and p modes. Hence, in the following we assume that the turbulent field, and its spectral dependence, are not affected by uniform rotation. Note, however, that for lower frequencies, and especially asymptotic gravity-modes, this approximation is no longer valid since a significant contribution to the mode excitation comes from the deeper convective layers (Belkacem et al. 2009).
We then consider the effect of the perturbation of the
mode excitation rates by the Coriolis acceleration associated with the modification of the eigenfunctions.
In this framework, we use a perturbative approach,
which is valid for slow rotators and particularly for the Sun
since we restrict our investigation to rather high-frequency p and g modes.
The ratio of the mode frequency to the rotation rate is still higher than unity. In the Sun, for a typical p mode
at ![]() mHz, one has
mHz, one has
![]() in
the convective region where modes are excited,
and for a solar g mode at
in
the convective region where modes are excited,
and for a solar g mode at
![]() Hz, this ratio remains high at
Hz, this ratio remains high at
![]() .
This allows us to use a perturbative approach.
.
This allows us to use a perturbative approach.
3.1 Perturbation of the mode excitation rates
Our aim is to derive an analytical expression of excitation rates influenced by uniform rotation
using a perturbative method.
Following the classical method given in Unno et al. (1989), we develop the eigenfunction
for a given ![]() to first order
to first order
and for the toroidal part
| |
= | ![$\displaystyle i \left(\frac{2\Omega}{\omega_0}\right) \Bigg\{ \ell D_{\ell,m}\l...
...eft(0\right)}-\left(\ell-1\right)\xi_{{\rm H};n,\ell-1}^{\left(0\right)}\right]$](/articles/aa/full_html/2009/46/aa12284-09/img121.png)
|
|
![$\displaystyle -\left(\ell+1\right)D_{\ell+1,m}\left[\xi_{{\rm r};n,\ell+1}^{\le...
...t)}+\left(\ell+2\right)\xi_{{\rm H};n,\ell+1}^{\left(0\right)}\right] \Bigg\} ,$](/articles/aa/full_html/2009/46/aa12284-09/img122.png)
|
(32) |
where
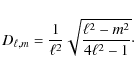
|
(33) |
The expression for
As pointed out by Dziembowski & Goode (1992), the convergence properties of the sum involved in Eq. (B.1) and Eq. (B.2) are unclear. As shown by Eq. (B.4), this is particularly problematic for a dense spectrum such as high-order gravity modes in the Sun. We nevertheless use it for convenience. An alternative exists (Dziembowski & Goode 1992), which consists of computing a modified eigenvalue problem. However, this second possibility makes it more difficult to identify contributions to the excitation rates.
Inserting the decomposition (Eqs. (B.1) to (B.3)) into Eqs. (15) and (16), we obtain (see Appendix B for the detailed calculation)
where
and
We now define the excitation rates asymmetry, between prograde and retrograde modes to first order such as
From Eq. (37), two factors contribute to the asymmetry namely the ratio
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12284fig1.eps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{12284fig2.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12284-09/Timg135.png)
|
Figure 1:
Top: excitation rates for the mode |
| Open with DEXTER | |
3.2 Application to slow rotators
3.2.1 The Sun
Using the same numerical computation as described in Belkacem et al. (2008), we apply this
formalism (Eqs. (34)-(36)) to the solar case.
Figure 1 displays the mode excitation rates for the ![]() ,
p and g modes.
It also presents the ratio
,
p and g modes.
It also presents the ratio
![]() ,
defined in Eq. (37), which emphasizes
the effect of the mode excitation rate asymmetry between the prograde and retrograde modes.
,
defined in Eq. (37), which emphasizes
the effect of the mode excitation rate asymmetry between the prograde and retrograde modes.
It turns out that the excitation rates of acoustic modes are modified
with an excitation rate asymmetry of the order of the percent, which
increases toward g modes.
We find that the variation in the mode excitation-rate asymmetry with frequency
is caused by the term
![]() in Eq. (37), while the ratio
P|m|(1) / P(0)remains of the order of the value of one.
P|m|(1) is dominated by the first term in Eq. (B.12),
which corresponds to the contribution of the radial component
of the eigenfunction, for p modes.
For g modes, the horizontal component of the eigenfunction
is also of importance and contributes significantly to
P|m|(1).
in Eq. (37), while the ratio
P|m|(1) / P(0)remains of the order of the value of one.
P|m|(1) is dominated by the first term in Eq. (B.12),
which corresponds to the contribution of the radial component
of the eigenfunction, for p modes.
For g modes, the horizontal component of the eigenfunction
is also of importance and contributes significantly to
P|m|(1).
For higher values of the angular degree (![]() ), as
shown by Fig. 2, there are two effects.
First, the higher the azimuthal order m, the higher the mode excitation rates
asymmetry, at fixed
), as
shown by Fig. 2, there are two effects.
First, the higher the azimuthal order m, the higher the mode excitation rates
asymmetry, at fixed ![]() .
This is explained by the perturbation of the mode excitation rates
being proportional to m in Eq. (34).
Second, at fixed m, the higher the angular degree, the lower the mode excitation-rate
asymmetry.
This behavior comes from the frequency shift of high-
.
This is explained by the perturbation of the mode excitation rates
being proportional to m in Eq. (34).
Second, at fixed m, the higher the angular degree, the lower the mode excitation-rate
asymmetry.
This behavior comes from the frequency shift of high-![]() modes, since at fixed radial order,
the higher the angular degree the higher the mode frequency. Hence, for the same radial order
the ratio
modes, since at fixed radial order,
the higher the angular degree the higher the mode frequency. Hence, for the same radial order
the ratio
![]() will
decrease with the angular degree explaining the behavior in Fig. 2.
will
decrease with the angular degree explaining the behavior in Fig. 2.
3.2.2 The CoRoT target HD 49933
We now consider more rapid rotators, such
as HD 49933. This is an F5 V main-sequence star observed twice by the CoRoT mission![]() ,
first during 62 days and more recently for more than 150 days. The
unprecedented photometric precision achieved by the CoRoT mission (Auvergne et al. 2009; Michel et al. 2008a)
makes this star a good candidate for the detection of mode
excitation-rate asymmetry, which requires, as previously mentioned,
accurate measurements. This star, indeed, exhibits a surface rotation
period that is shorter than that of the Sun,
,
first during 62 days and more recently for more than 150 days. The
unprecedented photometric precision achieved by the CoRoT mission (Auvergne et al. 2009; Michel et al. 2008a)
makes this star a good candidate for the detection of mode
excitation-rate asymmetry, which requires, as previously mentioned,
accurate measurements. This star, indeed, exhibits a surface rotation
period that is shorter than that of the Sun,
![]() days (i.e.,
days (i.e.,
![]() )
as shown by Appourchaux et al. (2008), but still slow enough to ensure that the perturbative approach is valid.
)
as shown by Appourchaux et al. (2008), but still slow enough to ensure that the perturbative approach is valid.
In Fig. 3, we present the same ratio as in Fig. 2 for the ![]() ,
p
modes using a model of HD 49933 that matches
the seismic constraints derived by Appourchaux et al. (2008) (Goupil et al. 2009).
The asymmetry between the excitation rates of m=1 and m=-1 modes is
found to reach up to
,
p
modes using a model of HD 49933 that matches
the seismic constraints derived by Appourchaux et al. (2008) (Goupil et al. 2009).
The asymmetry between the excitation rates of m=1 and m=-1 modes is
found to reach up to ![]() .
In terms
of mode excitation-rate asymmetry, the differences between the Sun and HD 49933 is due to a higher ratio
.
In terms
of mode excitation-rate asymmetry, the differences between the Sun and HD 49933 is due to a higher ratio
![]() in Eq. (37).
in Eq. (37).
This demonstrates that an asymmetry in terms of mode excitation rates
is more likely to be observable for more rapid rotators than the Sun,
even if, in contrast to the Sun, only low-![]() modes are observed.
modes are observed.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{12284fig3.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12284-09/Timg140.png)
|
Figure 2:
Bias between prograde and retrograde modes, defined
in Eq. (37),
for four values of the azimuthal order m and the radial order n=5 as a function of the angular degree
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{12284fig4.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12284-09/Timg141.png)
|
Figure 3:
Bias between prograde and retrograde modes, for the |
| Open with DEXTER | |
4 Conclusion and perspectives
4.1 Conclusion
We have derived a formalism that models the stochastic excitation of oscillation modes by convective motions in uniformly rotating stellar regions. We have shown that the driving terms, due to rotation, that appear in the inhomogeneous wave equation are negligible with respect to the Reynolds stress contribution. We demonstrate that the dominant contribution to the excitation rates then comes from the modification of the eigenfunction by the Coriolis acceleration.
The formalism is then applied to low-order g modes and p modes of slow rotators,
and in particular the Sun and the CoRoT target HD 49933.
For the Sun, a bias between pro- and retrograde waves is found in
the excitation rates. For g modes, this bias can reach values of up to 10%. For low-![]() p modes, this bias is found to be of the order of a percent.
The detection of the mode excitation-rate asymmetry of individual p modes is not yet
possible since the observational error bars obtained, for instance by GOLF, are around
20% (Belkacem et al. 2006b), while we search for a physical effect of only several percent.
p modes, this bias is found to be of the order of a percent.
The detection of the mode excitation-rate asymmetry of individual p modes is not yet
possible since the observational error bars obtained, for instance by GOLF, are around
20% (Belkacem et al. 2006b), while we search for a physical effect of only several percent.
For more rapid rotators, such as HD49933, we find that the excitation-rate asymmetry
of low-![]() (
(![]() )
p modes can reach up to 10%.
However, this value is achieved at low frequency, where seismic measurements are generally dominated
by the granulation background. In the case of the CoRoT target HD 49933, detection of acoustic modes
is limited to the frequency domain
)
p modes can reach up to 10%.
However, this value is achieved at low frequency, where seismic measurements are generally dominated
by the granulation background. In the case of the CoRoT target HD 49933, detection of acoustic modes
is limited to the frequency domain
![]() mHz. In this frequency domain,
the asymmetry in P is no greater than 2%. In contrast, the 1-
mHz. In this frequency domain,
the asymmetry in P is no greater than 2%. In contrast, the 1-![]() uncertainties
associated with P are in the range 30%-80%, depending on the frequency, for the observations
completed during the CoRoT initial run (Appourchaux et al. 2008; Samadi et al. 2009).
For the second set of observations of HD 49933 by CoRoT, the 1-
uncertainties
associated with P are in the range 30%-80%, depending on the frequency, for the observations
completed during the CoRoT initial run (Appourchaux et al. 2008; Samadi et al. 2009).
For the second set of observations of HD 49933 by CoRoT, the 1-![]() uncertainties associated with P is expected to be lower, i.e., in the range 20%-40% (Benomar, private communication).
Furthermore, current seismic analyses (e.g., Appourchaux et al. 2008)
do not reproduce individual mode multiplets but assume a fixed
amplitude ratio of the different mode multiplets or even assume a fixed
amplitude ratio of the different
uncertainties associated with P is expected to be lower, i.e., in the range 20%-40% (Benomar, private communication).
Furthermore, current seismic analyses (e.g., Appourchaux et al. 2008)
do not reproduce individual mode multiplets but assume a fixed
amplitude ratio of the different mode multiplets or even assume a fixed
amplitude ratio of the different ![]() degree.
Therefore, despite the high precision of the CoRoT instrument, it is presently not possible
to constraint P for an individual mode multiplet (i.e., for a given value of
degree.
Therefore, despite the high precision of the CoRoT instrument, it is presently not possible
to constraint P for an individual mode multiplet (i.e., for a given value of ![]() and m).
Concerning the Kepler instrument, its performance in terms of photon noise level
is expected to be a factor five lower in terms of power compared to that achieved for the brightest stars
of the CoRoT mission (Chaplin et al. 2008). On the other hand, Kepler will observe the seismic
targets over a much longer period (around 4 years) than the CoRoT mission, which
we hope will permit us to constrain individual mode multiplets.
Another way to proceed is to consider a sum of P for a given m so as to reduce the actual
observational errorbars in both the Solar case and that of HD49933.
and m).
Concerning the Kepler instrument, its performance in terms of photon noise level
is expected to be a factor five lower in terms of power compared to that achieved for the brightest stars
of the CoRoT mission (Chaplin et al. 2008). On the other hand, Kepler will observe the seismic
targets over a much longer period (around 4 years) than the CoRoT mission, which
we hope will permit us to constrain individual mode multiplets.
Another way to proceed is to consider a sum of P for a given m so as to reduce the actual
observational errorbars in both the Solar case and that of HD49933.
We note that mode amplitude is a balance between driving and damping. Therefore, asymmetries in mode amplitudes cannot be inferred only from excitation rates since some possible asymmetry in the mode damping rate can arise. This is not investigated here but left to future work.
4.2 Perspectives
The effect of uniform rotation on the mode amplitude excitation rates presented here is exploratory work that requires further investigation and theoretical developments.
Stellar convection zones are differentially rotating. Therefore, the next step would be to take the differential rotation into account in both the radial and the latitudinal directions. In contrast to uniform rotation, a consideration at Eq. (10) permits us to understand that the driving source terms in the inhomogeneous wave equation Eq. (4) are modified by differential rotation. The effect of differential rotation on mode excitation rates is the scope of an upcoming paper.
The regime of rapid rotation should also be addressed. The formalism must be adapted to the specific geometry of those stars, since spherical coordinates become inappropriate and one may have to take the star deformation into account. In addition, the eigenfunctions and frequencies have to be derived from an adapted non-perturbative method (e.g., Reese et al. 2006) since rotation can strongly modify both the eigenfunctions and the stellar structure of a star (Rieutord & Valdettaro 1997; Reese et al. 2006; Dintrans & Rieutord 2000). Furthermore, in such a regime new types of waves appear that deserve a further study, such as inertial waves and gravito-inertial waves (Rieutord & Valdettaro 1997; Mathis et al. 2008; Dintrans & Rieutord 2000). In addition, in contrast to slow rotators, the turbulent field is also affected by rotation and the spectral description of turbulence must be taken it into account. The assumption of isotropic turbulence is should then be excluded and the spectral properties of the turbulent field be specified. Numerical simulations can be of some help. As done for solar g modes using the ASH code (Belkacem et al. 2009), it is possible to assess the turbulent properties of these rotators from numerical simulations.
AcknowledgementsK.B. acknowledges financial support from Liège University through the subside fédéral pour la recherche.
Appendix A: Detailed expressions for the Reynolds source term
The eigenfunctions (![]() )
are developed in spherical coordinates
)
are developed in spherical coordinates
![]() and expanded as a sum over spherical harmonics.
Hence the fluid displacement eigenfunction for
a mode with given
and expanded as a sum over spherical harmonics.
Hence the fluid displacement eigenfunction for
a mode with given ![]() is written as
is written as
where the spherical harmonics (
with
The Reynolds stress contribution can be written as (see Belkacem et al. 2008, for details)
where
where the double dot denotes the tensor product.
To compute the coefficients bij in Eq. (A.3), we follow the procedure derived by Belkacem et al. (2008), which infers that
The contribution of the Reynolds stress can thus be written as:
where we have defined
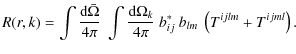
|
(A.7) |
Because Tijlm=Tjiml, it is easy to show that
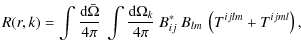
|
where
Using the expression Eq. (A.4) for Tijlm, we write
where
We assume isotropic turbulence, hence the
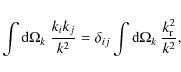
where
where we have set
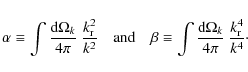
|
(A.11) |
Using Eq. (A.6) to compute Eq. (A.8), with
where we have defined
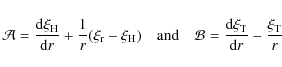
|
(A.13) |
while
![\begin{displaymath}{\cal F}_{\ell,\vert m\vert} = \frac{\vert m\vert (2 \ell + 1)}{2} \left[ \ell\left(\ell+1\right) - (m^2 + 1 )\right]
\end{displaymath}](/articles/aa/full_html/2009/46/aa12284-09/img191.png)
|
(A.14) |
with
Appendix B: First-order perturbation of the excitation rates
We recall the main results about the first-order perturbation of a spheroidal mode
![]() due to the Coriolis acceleration (of frequency
due to the Coriolis acceleration (of frequency
![]() )
and establish the perturbation of the excitation rates.
Following the classical method given in Unno et al. (1989), we obtain
)
and establish the perturbation of the excitation rates.
Following the classical method given in Unno et al. (1989), we obtain
and
where
and
![$\displaystyle z_{l,m}=l D_{l,m}\left[\xi_{{\rm r};n,l-1}^{\left(0\right)}-\left...
...^{\left(0\right)}+\left(l+2\right)\xi_{{\rm H};n,l+1}^{\left(0\right)}\right] ,$](/articles/aa/full_html/2009/46/aa12284-09/img199.png)
|
(B.5) |
where
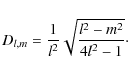
|
(B.6) |
The Coriolis corrective terms are of the order of
![\begin{displaymath}C_{{\rm R},m}^{2}=\left[C_{{\rm R}}^{\left(0\right)}\right]^2...
...right)\left[C_{{\rm R},\vert m\vert}^{\left(1\right)}\right]^2
\end{displaymath}](/articles/aa/full_html/2009/46/aa12284-09/img201.png)
|
(B.7) |
where
![\begin{displaymath}\left[C_{{\rm R}}^{\left(0\right)}\right]^{2}=4\pi^3\int{\rm d}m \; R^{\left(0\right)}S_{R}\left(\omega_{0}\right) ,
\end{displaymath}](/articles/aa/full_html/2009/46/aa12284-09/img202.png)
|
(B.8) |
![\begin{displaymath}\left[C_{{\rm R},\vert m\vert}^{\left(1\right)}\right]^{2}=4\...
...{\vert m\vert}^{\left(1\right)} S_{R}\left(\omega_{0}\right) ,
\end{displaymath}](/articles/aa/full_html/2009/46/aa12284-09/img203.png)
|
(B.9) |
and
| |
= | 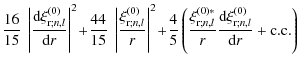
|
|
![$\displaystyle + L^2 \left[ {11\over 15} ~ \left( \left\vert \mathcal{A} \right\...
...\right)*} \xi_{{\rm H};n,l}^{\left(0\right)}}{r^2} + {\rm c.c.} \right) \right]$](/articles/aa/full_html/2009/46/aa12284-09/img207.png)
|
|||
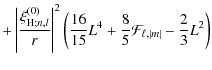
|
|||
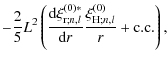
|
(B.10) |
where
Similarly, we get for the entropic term given in Eq. (21)
![\begin{displaymath}C_{S}^{2}=\left[C_{S}^{\left(0\right)}\right]^2+\left(\frac{2...
...}{\omega_{0;n,l}}\right)m\left[C_{S}^{\left(1\right)}\right]^2
\end{displaymath}](/articles/aa/full_html/2009/46/aa12284-09/img219.png)
|
(B.13) |
where
![\begin{displaymath}\left[C_{S}^{\left(0\right)}\right]^{2}=\frac{4\pi^3{\mathcal...
...+B_{l}^{\left(0\right)}\right)S_{S}\left(\omega_{0;n,l}\right)
\end{displaymath}](/articles/aa/full_html/2009/46/aa12284-09/img220.png)
|
(B.14) |
and
![\begin{displaymath}\left[C_{S}^{\left(1\right)}\right]^{2}=\frac{4\pi^3{\mathcal...
...B_{l}^{\left(1\right)}\right)S_{S}\left(\omega_{0;n,l}\right).
\end{displaymath}](/articles/aa/full_html/2009/46/aa12284-09/img221.png)
|
(B.15) |
We have
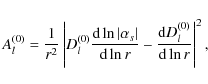
|
(B.16) |
| |
= | 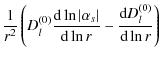
|
|
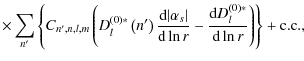
|
(B.17) |
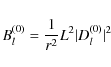
|
(B.18) |
and
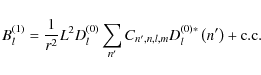
|
(B.19) |
where
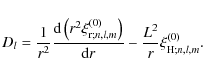
|
(B.20) |
References
- Appourchaux, T., Fröhlich, C., Andersen, B., et al. 2000, ApJ, 538, 401 [NASA ADS] [CrossRef]
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [CrossRef] [EDP Sciences]
- Balmforth, N. J. 1992, MNRAS, 255, 639 [NASA ADS]
- Belkacem, K., Samadi, R., Goupil, M. J., & Kupka, F. 2006a, A&A, 460, 173 [NASA ADS] [CrossRef] [EDP Sciences]
- Belkacem, K., Samadi, R., Goupil, M. J., Kupka, F., & Baudin, F. 2006b, A&A, 460, 183 [NASA ADS] [CrossRef] [EDP Sciences]
- Belkacem, K., Samadi, R., Goupil, M.-J., & Dupret, M.-A. 2008, A&A, 478, 163 [NASA ADS] [CrossRef] [EDP Sciences]
- Belkacem, K., Samadi, R., Goupil, M. J., et al. 2009, A&A, 494, 191 [NASA ADS] [CrossRef] [EDP Sciences]
- Chaplin, W. J., Appourchaux, T., Arentoft, T., et al. 2008, Astron. Nachr., 329, 549 [NASA ADS] [CrossRef]
- Chaplin, W. J., Houdek, G., Elsworth, Y., et al. 2005, MNRAS, 360, 859 [NASA ADS] [CrossRef]
- Christensen-Dalsgaard, J., Arentoft, T., Brown, T. M., et al. 2008, Commun. Asteroseismol., 157, 266 [NASA ADS]
- Decressin, T., Mathis, S., Palacios, A., et al. 2009, A&A, 495, 271 [NASA ADS] [CrossRef] [EDP Sciences]
- Dintrans, B., & Rieutord, M. 2000, A&A, 354, 86 [NASA ADS]
- Dziembowski, W. A., & Goode, P. R. 1992, ApJ, 394, 670 [NASA ADS] [CrossRef]
- Espinosa Lara, F., & Rieutord, M. 2007, A&A, 470, 1013 [NASA ADS] [CrossRef] [EDP Sciences]
- Gabriel, A. H., Baudin, F., Boumier, P., et al. 2002, A&A, 390, 1119 [NASA ADS] [CrossRef] [EDP Sciences]
- García, R. A., Jiménez, A., Mathur, S., et al. 2008a, Astron. Nachr., 329, 476 [NASA ADS] [CrossRef]
- García, R. A., Mathur, S., & Ballot, J. 2008b, Sol. Phys., 251, 135 [NASA ADS] [CrossRef]
- García, R. A., Turck-Chièze, S., Jiménez-Reyes, S. J., et al. 2007, Science, 316, 1591 [NASA ADS] [CrossRef]
- Goldreich, P., & Keeley, D. A. 1977, ApJ, 212, 243 [NASA ADS] [CrossRef]
- Goldreich, P., Murray, N., & Kumar, P. 1994, ApJ, 424, 466 [NASA ADS] [CrossRef]
- Goupil, M., Deheuvels, S., Provost, J., et al. 2009, A&A, submitted
- Houdek, G. 2006, in SOHO 18/GONG 2006/HeIAS I: beyond the spherical Sun, ed. K. Fletcher, ESA SP-624, Noordwijk [arXiv:astro-ph/0612024]
- Kumar, P., Narayan, R., & Loeb, A. 1995, ApJ, 453, 480 [NASA ADS] [CrossRef]
- Leibacher, J. W., & Stein, R. F. 1971, Astrophys. Lett., 7, 191 [NASA ADS]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Berlin, Heidelberg: Springer), Astron. Astrophys. Library
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef]
- Mathis, S., Talon, S., Pantillon, F.-P., & Zahn, J.-P. 2008, Sol. Phys., 251, 101 [NASA ADS] [CrossRef]
- Mathur, S., Eff-Darwich, A., García, R. A., & Turck-Chièze, S. 2008, A&A, 484, 517 [NASA ADS] [CrossRef] [EDP Sciences]
- Mathur, S., Turck-Chièze, S., Couvidat, S., & García, R. A. 2007, ApJ, 668, 594 [NASA ADS] [CrossRef]
- Michel, E., Baglin, A., Auvergne, M., et al. 2008a, Science, 322, 558 [NASA ADS] [CrossRef]
- Michel, E., Baglin, A., Weiss, W. W., et al. 2008b, Commun. Asteroseismol., 157, 69 [NASA ADS]
- Miesch, M. S. 2005, Liv. Rev. Sol. Phys., 2, 1
- Reese, D., Lignières, F., & Rieutord, M. 2006, A&A, 455, 621 [NASA ADS] [CrossRef] [EDP Sciences]
- Rieutord, M., & Valdettaro, L. 1997, J. Fluid Mech., 341, 77 [NASA ADS] [CrossRef]
- Samadi, R., & Goupil, M. J. 2001, A&A, 370, 136 [NASA ADS] [CrossRef] [EDP Sciences]
- Samadi, R., Ludwig, H., Belkacem, K., et al. 2009, A&A, in press [arXiv:0910.4027]
- Samadi, R., Nordlund, Å., Stein, R. F., Goupil, M. J., & Roxburgh, I. 2003, A&A, 403, 303 [NASA ADS] [CrossRef] [EDP Sciences]
- Stein, R., Georgobiani, D., Trampedach, R., Ludwig, H.-G., & Nordlund, Å. 2004, Sol. Phys., 220, 229 [NASA ADS] [CrossRef]
- Stein, R. F. 1967, Sol. Phys., 2, 385 [NASA ADS] [CrossRef]
- Talon, S., Zahn, J.-P., Maeder, A., & Meynet, G. 1997, A&A, 322, 209 [NASA ADS]
- Turck-Chièze, S., García, R. A., Couvidat, S., et al. 2004, ApJ, 604, 455 [NASA ADS] [CrossRef]
- Ulrich, R. K. 1970, ApJ, 162, 993 [NASA ADS] [CrossRef]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial oscillations of stars (University of Tokyo Press), 2nd edn.
Footnotes
- ... terms
![[*]](/icons/foot_motif.png)
- Linear terms are defined as the product of an equilibrium quantity and a fluctuating one.
- ... mission
![[*]](/icons/foot_motif.png)
- The CoRoT space mission, launched on December 27th 2006, has been developed and is operated by CNES, with the contribution of Austria, Belgium, Brazil , ESA (RSSD and Science Program), Germany and Spain.
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{12284fig1.eps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{12284fig2.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12284-09/Timg135.png)
|
Figure 1:
Top: excitation rates for the mode |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{12284fig3.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12284-09/Timg140.png)
|
Figure 2:
Bias between prograde and retrograde modes, defined
in Eq. (37),
for four values of the azimuthal order m and the radial order n=5 as a function of the angular degree
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{12284fig4.eps}
\end{figure}](/articles/aa/full_html/2009/46/aa12284-09/Timg141.png)
|
Figure 3:
Bias between prograde and retrograde modes, for the |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



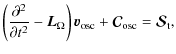
![$\displaystyle - \frac {\partial } {\partial t} \left[ \rho_{\rm t} \left( \Omeg...
...in \theta~ \vec u_{\rm t} \cdot \vec \nabla \Omega~ \vec e_\phi \right) \right]$](/articles/aa/full_html/2009/46/aa12284-09/img39.png)
![$\displaystyle \frac {\partial } {\partial t} (\rho_{\rm t} \vec g_1) + \vec \na...
..._{\rm t}\right)\right]
- \vec g \vec \nabla \cdot (\rho_{\rm t} \vec u_{\rm t})$](/articles/aa/full_html/2009/46/aa12284-09/img41.png)
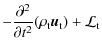
![\begin{displaymath}
\vec v_{\rm osc} = A~ \left[i \sigma\vec \xi - (\vec \xi \cd...
...sin \theta ~ \vec e_{\phi}\right] {\rm e}^{{\rm i} \sigma t} ,
\end{displaymath}](/articles/aa/full_html/2009/46/aa12284-09/img46.png)
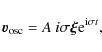
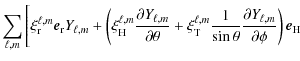
![$\displaystyle + \left( \xi_{\rm H}^{\ell,m} \frac{1}{\sin \theta} \frac {\parti...
... \frac {\partial Y_{\ell,m} } {\partial \theta} \right) \vec e_{\rm T} \Bigg] ,$](/articles/aa/full_html/2009/46/aa12284-09/img55.png)
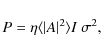
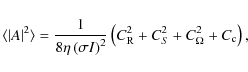
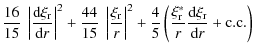
![$\displaystyle + ~ L^2 \left[ {11\over 15} ~ \left( \left\vert \mathcal{A} \righ...
...over 15} \left(\frac{\xi_{\rm r}^* \xi_{\rm H}}{r^2} +{\rm c.c.}\right) \right]$](/articles/aa/full_html/2009/46/aa12284-09/img71.png)
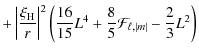
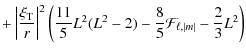
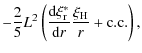
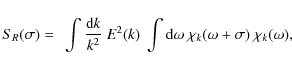
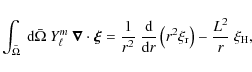
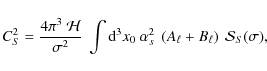
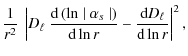
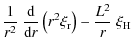
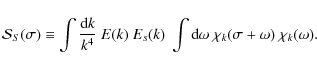
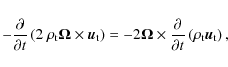
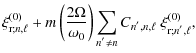
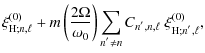
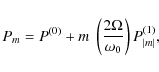
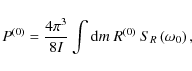
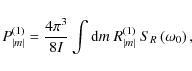
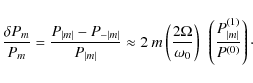
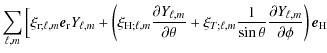
![$\displaystyle +
\left( \xi_{{\rm H};\ell,m} \frac{1}{\sin \theta} \frac {\parti...
...} \frac {\partial Y_{\ell,m} } {\partial \theta} \right) \vec e_{\rm T} \Big] ,$](/articles/aa/full_html/2009/46/aa12284-09/img145.png)
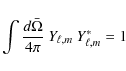
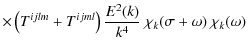
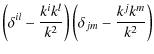
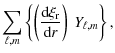
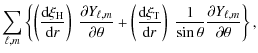
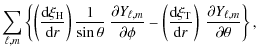
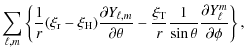
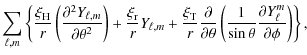
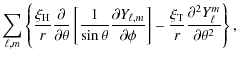
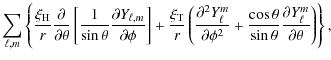
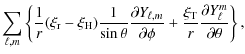
![$\displaystyle \displaystyle\sum_{\ell,m}\left\{ \frac{\xi_{\rm r}}{r} Y_{\ell,m...
...\left ( \frac {\partial Y_{\ell,m} } {\partial \theta} \right ) \right ]\right.$](/articles/aa/full_html/2009/46/aa12284-09/img169.png)
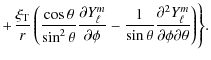
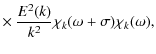
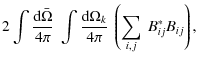
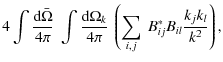
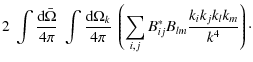
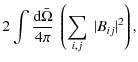
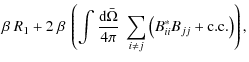
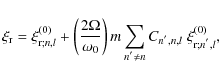
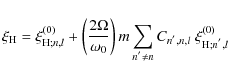
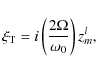
![$\displaystyle C_{n^{'},n,l}=\frac{\omega_{0}^{2}}{\left(\omega_{0}^{2}-\omega_{...
...\right)}\right)\xi_{{\rm H};n^{'},l}^{\left(0\right)*}\right]\rho_0 r^2{\rm d}r$](/articles/aa/full_html/2009/46/aa12284-09/img198.png)
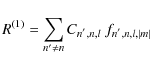
![$\displaystyle \frac{16}{15}\left[\frac{{\rm d}\xi_{{\rm r};n,l}^{\left(0\right)...
...rac{{\rm d}\xi_{{\rm r};n^{'},l}^{\left(0\right)*}}{{\rm d}r}+{\rm c.c.}\right]$](/articles/aa/full_html/2009/46/aa12284-09/img211.png)
![$\displaystyle +\frac{44}{15}\left[\frac{\xi_{{\rm r};n,l}^{\left(0\right)}\xi_{{\rm r};n^{'},l}^{\left(0\right)*}}{r}+{\rm c. c.}\right]$](/articles/aa/full_html/2009/46/aa12284-09/img212.png)
![$\displaystyle +\left(\frac{16}{15}L^4-\frac{2}{3}L+\frac{8}{5}{\mathcal F}_{l,\...
...\left(0\right)}\xi_{{\rm H};n^{'},l}^{\left(0\right)*}}{r^2}+{\rm c. c.}\right]$](/articles/aa/full_html/2009/46/aa12284-09/img213.png)
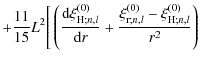
![$\displaystyle \times\left(\frac{{\rm d}\xi_{{\rm H};n^{'},l}^{\left(0\right)*}}...
...right)*}-\xi_{{\rm H};n^{'},l}^{\left(0\right)*}}{r^2}\right)+{\rm c. c.}\Bigg]$](/articles/aa/full_html/2009/46/aa12284-09/img215.png)