EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 505 / No 1 (October I 2009) A&A, 505 1 (2009) 169-176 Full HTML
Free Access
Issue
A&A
Volume 505, Number 1, October I 2009
Page(s) 169 - 176
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200911948
Published online 24 July 2009

Cosmic ray acceleration parameters from multi-wavelength observations. The case of SN 1006

E. G. Berezhko1 - L. T. Ksenofontov1 - H. J. Völk2

1 - Yu. G. Shafer Institute of Cosmophysical Research and Aeronomy, 31 Lenin Ave., 677980 Yakutsk, Russia
2 - Max-Planck-Institut für Kernphysik, Postfach 103980, 69029 Heidelberg, Germany

Received 25 February 2009 / Accepted 11 June 2009

Abstract
Aims. The properties of the Galactic supernova remnant (SNR) SN 1006 are theoretically reanalysed.
Methods. Nonlinear kinetic theory is used to determine the acceleration efficiency of cosmic rays (CRs) in the supernova remnant SN 1006. The known range of astronomical parameters and the existing measurements of nonthermal emission are examined in order to define the values of the relevant physical parameters that determine the CR acceleration efficiency.
Results. It is shown that the parameter values - proton injection rate, electron to proton ratio and downstream magnetic field strength -are determined with the appropriate accuracy. In particular the observed azimuthal variations in the $\gamma $-ray  morphology also agree with the theoretical expectation. These parameter values, together with the reduction of the $\gamma $-ray   flux relative to a spherically symmetric acceleration geometry, allow a good fit to the existing data, including the recently detected TeV emission by H.E.S.S.
Conclusions. SN 1006 represents the first example where a high efficiency of nuclear CR production, required for the Galactic CR sources, is consistently established.

Key words: ISM: cosmic rays - acceleration of particles - shock waves - stars: supernovae: individual: SN 1006 - radiation mechanisms: nonthermal - gamma rays: theory

1 Introduction

Cosmic rays (CRs) below an energy of 1017 eV are believed to be accelerated in the shell-type supernova remnants (SNRs) of our Galaxy (e.g. Berezhko & Völk 2007) by means of the diffusive shock acceleration process. However, this proposition still has only a limited observational/theoretical basis. In addition, SNRs may not only act individually but possibly also more collectively in the environment of interacting stellar winds and supernova explosions in OB associations (e.g. Parizot et al. 2004; Binns et al. 2007). To ensure that Galactic SNRs are indeed efficient sources of the Galactic CRs, a number of SNRs is required with clearly determined astronomical parameters, like the type of supernova explosion, the SNR age, the distance, and the properties of the circumstellar medium. Applying an appropriate model which consistently describes the dynamics of the SNR to such SNRs, one can then predict the properties of the accelerated particles and the dynamical and radiative effects which they produce, like the shock modification and the multi-wavelength nonthermal emission.

The success of the theoretical model can be judged by comparison with the experimentally determined overall broad band spectrum and with the morphological characteristics of the SNR, like its filament structures and the general radial and azimuthal variations of the emission pattern, as well as the internal dynamics characterized by the contact discontinuity between ejected and swept-up mass. From the point of view of Galactic CR origin, the key quantity is the efficiency of CR production.

In practice such a program is most often hampered by the limited amount and detail of relevant observations. First of all, the astronomical parameters of SNRs are as a rule poorly known. Even though the SNR age is known for several historical SNRs, the distance is usually quite uncertain. In this regard, SN 1006 is an exception: the distance was determined using optical measurements with relatively high precision (Winkler et al. 2003).

The second problem is that even the presently most advanced nonlinear kinetic theory of CR acceleration in SNRs (Berezhko & Völk 1997; Berezhko et al. 1996)[*] contains physical parameters that cannot yet be theoretically calculated with the necessary precision (see Völk 2004, for a review). This concerns the magnitude and the spatial distribution of the injection rates of ions and of electrons into the diffusive shock acceleration process as well as the extent of magnetic field amplification in this process. Fortunately, the values of these parameters can be inferred from the observed radio and X-ray synchrotron spectra if they are measured in sufficient detail (see Berezhko 2008,2005, for reviews). In such a case, this theory provides a consistent if still approximate model of both SNR and CR dynamics, and of the properties of the emission produced by the accelerated particles. In particular, the theory predicts the high-energy $\gamma $-ray  spectrum.

Up to now SN 1006 has been the only example for which all astronomical parameters are quite well known (e.g. Cassam-Chenaï et al. 2008). In addition, the nonthermal emission in the radio and X-ray bands has by now been measured quite accurately with Chandra (Allen et al. 2008,2004) and Suzaku (Bamba et al. 2008). Beyond that, the VHE emission of SN 1006 has been recently detected with H.E.S.S., both regarding its flux and its morphology (Naumann-Godo et al. 2009). This makes SN 1006 uniquely suitable for theoretical study and for a detailed comparison with the experimental data.

We have already applied this nonlinear theory to the case of SN 1006 before (Ksenofontov et al. 2005; Berezhko et al. 2002; Völk et al. 2003,2008b; Berezhko et al. 2003; Völk et al. 2005). In the following, a brief review of this previous work is given. The corresponding model assumes spherical symmetry and a quasi-parallel shock. However it was argued that efficient nuclear particle injection/acceleration should arise only within two polar cap regions, where the SN shock is quasi-parallel with respect to the ambient ISM magnetic field which in turn is approximately perpendicular to the line of sight (Völk et al. 2003). The calculated size of the efficient nuclear CR production regions, which amounts to about 20% of the shock surface, corresponds very well to the observed sizes of the bright X-ray synchrotron emission regions. Over the remaining 80% of the surface, the shock is quasi-perpendicular and this leads to a depression of the injection of nuclear particles into the diffusive shock acceleration process. This means that efficient nuclear CR production - that occurs in a spherically symmetric model uniformly across the whole shock surface - in the actual SNR takes place only within the polar regions. It is therefore consistent with a correction for the spherically symmetric solution for nuclear CR production and the associated $\gamma $-ray  emission by a renormalization factor $f_{\rm re} \approx 0.2$ (for details, see the Appendix; to emphasize the three-dimensional character of the configuration a description in terms of magnetic flux tubes is given.). In the first study (Berezhko et al. 2002), it was demonstrated that the observed properties of the nonthermal emission can be consistently understood assuming a considerably amplified magnetic field $B_{\rm d}\approx 120$ $\mu $G within the nuclear injection/acceleration region. Such a strong magnetic field is consistent with theoretical expectations and was confirmed by the Chandra detection (Long et al. 2003; Bamba et al. 2003) of filament structures in the nonthermal X-ray emission of the rims of the SNR shell (see Berezhko et al. 2003, for an interpretation). A filamentary structure of this character is indeed expected in young SNRs, where the magnetic field is strongly amplified, as the result of the strong synchrotron losses of the X-ray emitting CR electrons. In fact, since there generally exists a simple relation between the filament thickness and the interior magnetic field strength (Berezhko & Völk 2004a), the measurement of the filament thickness represents a new and independent method for the determination of the magnetic field strength inside young SNRs. It is important to note that the interior magnetic field strength, determined in such a way for all known Galactic SNRs, agrees very well with its value derived from a fit of the shape of the overall synchrotron spectra, wherever both methods can be applied (Völk et al. 2005). It was also shown (Berezhko et al. 2002) that nonlinear kinetic theory of CR acceleration is consistent with the TeV-emission detected by CANGAROO in 1998 for a value $N_{\rm H}=0.3$ cm-3 of the ambient interstellar medium ISM density from the range $0.05 \leq N_{\rm H} \leq 0.3$ cm-3existing in the literature. However, SN 1006 was not confirmed as a TeV source by the H.E.S.S. experiment in a total of 18.2h (in 2003) and 6.3h (in 2004) ``livetime'' of ON source observations with SN 1006 in the field of view (Aharonian et al. 2005). The H.E.S.S. upper limit was roughly one order of magnitude lower than the published CANGAROO flux. In a subsequent paper by the present authors (Ksenofontov et al. 2005) it was demonstrated that this H.E.S.S. upper limit does not invalidate the theoretical picture on which the previous calculation of the $\gamma $-ray  emission spectrum had been based. As it was shown, it is rather the value of the external astronomical parameter $N_{\rm H}$ that strongly influences the hadronic $\gamma $-ray  flux: the hadronic $\gamma $-ray  flux is very sensitive to the ambient gas density $N_{\rm H}$ and the H.E.S.S. upper limit requires $N_{\rm H} < 0.1$ cm-3. It is important that only a rather strongly amplified magnetic field, produced nonlinearly by efficiently accelerated nuclear CRs, is compatible with such a low $\gamma $-ray  flux, which is therefore expected to be predominantly of hadronic origin. Otherwise the overproduction of accelerated electrons would lead to an unacceptably high inverse Compton (IC) $\gamma $-ray  emission (Berezhko et al. 2002). This requires a strong component of accelerated nuclear particles whose energy density substantially exceeds that of the synchrotron electrons. The opposite simplest IC scenario, which is based on the assumption that the entire nonthermal SNR emission is produced by accelerated electrons without any substantial nuclear CR production and magnetic field amplification, substantially overpredicts the existing $\gamma $-ray  upper limits for all known type Ia Galactic SNRs (Völk et al. 2008b).

Since TeV $\gamma $-ray  emission of SN 1006 was recently detected (Naumann-Godo et al. 2009) it is worthwhile to reconsider SN 1006 on the basis of this nonlinear theory. Compared with the previous consideration (Ksenofontov et al. 2005) this makes it possible to determine the ambient ISM density within narrow limits. In addition, we shall demonstrate that the values of the relevant physical parameters - proton injection rate, electron to proton ratio and downstream magnetic field strength - are determined for SN 1006 with appropriate accuracy from the measured synchrotron spectrum. The $\gamma $-ray  morphology agrees with the theoretical expectations regarding the morphology of ion injection and the corresponding morphology of magnetic field amplification (Völk et al. 2003). It is therefore indeed consistent with a correction for the total nuclear particle pressure and the total $\gamma $-ray  flux obtained in the spherically symmetric solution by a renormalization factor $f_{\rm re} \approx 0.2$. The correction implies the full value of particle pressure and $\gamma $-ray  flux, as calculated in the spherically symmetric model, in the quasi-parallel part of the magnetic flux tubes that thread the polar cap regions, but a value of zero elsewhere. The above parameter values plus the mentioned morphological aspects allow a physical explanation of all existing multi-wavelength data, including the H.E.S.S. measurement of the TeV spectrum. There is possibly one exception to this conclusion. It concerns the radius of the contact discontinuity between ejected and swept-up mass relative to the radius of the SNR blast wave, cf. recent data discussed by Cassam-Chenaï et al. (2008) which indicate a large value - apparently quite close to unity - of this ratio. However another very recent analysis (Miceli et al. 2009) claims values $\sim $0.9 for this ratio which are rather in line with quantitative expectations for a CR-modified shock in an object of comparable evolutionary phase like Tycho's SNR (Warren et al. 2005; Völk et al. 2008a; Cassam-Chenaï et al. 2007). Future work will have to assess these differences.

2 Results and discussion

Since SN 1006 is a type Ia supernova it presumably expands into a uniform ISM, ejecting roughly a Chandrasekhar mass $M_{\rm ej}=1.4~ M_{\odot}$. Since the gas density indeed varies only mildly across the SNR (Acero et al. 2007), it appears reasonable to assume also the circumstellar magnetic field to be uniform. The ISM mass density $\rho_0=1.4m_{\rm p}N_{\rm H}$, which is usually characterized by the hydrogen number density $N_{\rm H}$, is an important parameter which strongly influences the expected SNR dynamics and nonthermal emission.

As in our earlier study (Ksenofontov et al. 2005) we solve here the coupled set of nonlinear equations. mentioned before, in order to find the optimum set of physical parameters of SN 1006 which gives a consistent description of the observed overall dynamics and of the nonthermal emission together with its morphology. The theory includes all the important physical factors that influence CR acceleration and SNR dynamics: shock modification by the CR backreaction, MHD wave damping within the shock transition, a consistently determined CR spectrum, and the spatial distributions in each evolutionary phase. In addition, it includes synchrotron losses of CR electrons and a determination of all nonthermal emission processes produced in SNRs by the accelerated CRs. It had also been shown that the values of the key parameters (proton injection rate $\eta $, electron to proton ratio $K_{\rm ep}$ and interior (downstream) magnetic field strength $B_{\rm d}$) which cannot be predicted theoretically with the required accuracy, can be determined from a fit of the observed synchrotron emission data. It is of importance here that the parameter values for SN 1006, determined in this way, were very well confirmed by the Chandra measurements of the fine structure of the nonthermal X-ray emission (Long et al. 2003; Bamba et al. 2003), as analyzed by Berezhko et al. (2003).

Compared with the previous study (Ksenofontov et al. 2005), the analysis includes the most accurate X-ray data from Chandra (Allen et al. 2004) and Suzaku (Bamba et al. 2008) that make it possible to quite precisely determine the acceptable range of these parameter values. Also a time-dependent, amplified upstream magnetic field

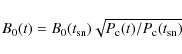\begin{displaymath}B_0(t)=B_0(t_{\rm sn})\sqrt{P_{\rm c}(t)/P_{\rm c}(t_{\rm sn})} \end{displaymath} (1)

is used - in the spherically symmetric calculation over the entire shock surface - where $P_{\rm c}$ is the CR pressure and $t_{\rm sn}$ is the SNR age (see Berezhko & Völk 2004b). The value of the magnetic field at the current epoch $B_0(t_{\rm sn})$ is determined as a result of the best fit of the measured synchrotron spectrum (see below). In the downstream region, the magnetic field is assumed to be frozen into the gas with the postshock field value $B_2 \approx \sigma B_0$, where $\sigma$ is the shock compression ratio. Under these assumptions, the magnetic field strength varies only slightly within the downstream region of swept-up ISM. Therefore, below, the value $B_{\rm d}=B_2$ is used as the interior magnetic field strength. Also the notations $B_{\rm d}$ and B0 are used for their values at the current SNR epoch $t=t_{\rm sn}$.

 \begin{figure} \par\includegraphics[width=8.5cm,clip]{11948fg1.eps} \end{figure} Figure 1:

Gas dynamical evolution for the two values of the total explosion energy $E_{\rm sn}= 1.8\times 10^{51}$ erg and $E_{\rm sn}= 1.5\times 10^{51}$ that correspond to the values $N_{\rm H}=0.05~\mbox{cm}^{-3}$ and $N_{\rm H}=0.035~\mbox{cm}^{-3}$ of the ISM hydrogen number density, respectively. The quantities $R_{\rm s}$ and $V_{\rm s}$ denote the shock radius and the shock velocity, their time evolution being fitted to the observed values shown. The vertical dotted line indicates the present epoch.
Open with DEXTER

Since the properties of accelerated CR nuclear and electron spectra and their dependence on the relevent physical parameters, as well as the dynamical properties of the system, were described in detail in previous papers (e.g Ksenofontov et al. 2005; Berezhko et al. 2002), they will not be discussed here (see however the Appendix for a summary).

The values of the SN explosion energy $E_{\rm sn}= 1.8\times 10^{51}$ erg and $E_{\rm sn}= 1.5\times 10^{51}$ erg are taken to fit the observed shock size $R_{\rm s}$ and shock speed $V_{\rm s}$(Moffett et al. 1993) at the current epoch $t\approx 10^3$ yr (see Fig. 1) for the ISM hydrogen number densities $N_{\rm H}=0.05~\mbox{cm}^{-3}$ and $N_{\rm H}=0.035~\mbox{cm}^{-3}$, respectively. These densities are consistent with the observed level of the VHE emission (see below). Note that the calculation presented in Fig. 1 corresponds to the best fit value of the amplified upstream magnetic field strength B0=30 $\mu $G, even though the shock size $R_{\rm s}$ and shock speed $V_{\rm s}$ are quite insensitive to B0. The resulting current total shock compression ratios $\sigma$ for $N_{\rm H}=0.05~\mbox{cm}^{-3}$ and $N_{\rm H}=0.035~\mbox{cm}^{-3}$are $\sigma = 4.9$ and 4.7, respectively, whereas the subshock compression ratios $\sigma_{\rm s}$  are both close to $\sigma_{\rm s}=3.7$.

As the most reliable estimate for the distance the value d=2.2 kpc was taken (Winkler et al. 2003).

All these results stem mainly from the gas dynamics part of the governing equations.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11948fg2.eps} \end{figure} Figure 2:

Overall (=spatially integrated) spectra of energetic particles. Solid and dashed lines correspond to protons (p) and electrons (e), respectively.
Open with DEXTER

Figure 2 shows the volume-integrated momentumg distributions of energetic protons (representative for the nuclear component) and electrons. The proton cutoff energy $\epsilon_{\rm max}^{\rm p}$ is above 1015 eV. The electron spectral index $\gamma \approx 2$ equals that of the protons below the onset of synchrotron losses at the energy $\epsilon_l \approx 1$ TeV. The electron cutoff energy $\epsilon_{\rm max}^{\rm e}$ is near 1014 eV.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11948fg3.eps} \end{figure} Figure 3:

Differential synchrotron radio emission flux as a function of frequency, calculated for the ISM hydrogen number density $N_{\rm H}=0.05~\mbox{cm}^{-3}$ at the proton injection rate $\eta = 3\times 10^{-4}$, electron to proton ratio, $K_{\rm ep} = 4\times 10^{-4}$, and magnetic field strength B0=30 $\mu $G upstream of the subshock . The observed radio emission flux from a compilation of Allen et al. (2004) (see also Allen et al. 2008,2001) is shown.
Open with DEXTER

Figures 3-5 illustrate the consistency of the synchrotron spectrum, calculated for the ISM number density $N_{\rm H}=0.05~\mbox{cm}^{-3}$ with the best set of parameters ( $\eta = 3\times 10^{-4}$, $K_{\rm ep} = 4\times 10^{-4}$, B0=30 $\mu $G), with the observed spatially integrated spectra. Note that we use the differential synchrotron fluxes in the radio ($S_{\nu}$) and in the X-ray (d $F_{\gamma}$/d $\epsilon_{\gamma}$) range in a slightly different form. They are however simply connected by the relation $\nu S_{\nu}=\epsilon_{\gamma}^2$d $F_{\gamma}$/d $\epsilon_{\gamma}$.

It should be noted that the values $\alpha>0.5$ of the differential radio spectral index $\alpha= -{\rm d}\ln S_{\nu}$/d$\ln \nu$, as observed in young SNRs, require a curved electron spectrum that hardens to higher energies as predicted by nonlinear shock acceleration models, as originally emphasized by Reynolds & Ellison (1992). To have $\alpha=0.57$ in the radio range, as observed for SN 1006, one needs efficient CR acceleration with a proton injection rate $\eta = 3\times 10^{-4}$ which leads to the required shock modification, and a high interior magnetic field $B_{\rm d}\ge 130$ $\mu $G is required (Ksenofontov et al. 2005; Berezhko et al. 2002; Völk et al. 2005). The hardening of the observed radio synchrotron spectrum for SN 1006 has been recently demonstrated by Allen et al. (2008). Detailed X-ray synchrotron spectral measurements are, however, required to find the optimum value of the magnetic field strength $B_{\rm d}$ (Ksenofontov et al. 2005) since for a given fit of the calculated synchrotron spectrum in the radio range, the X-ray synchrotron amplitude is very sensitive to $B_{\rm d}$. The reason is the following: in the polar regions, where the scattering mean free path decreases down to the particle gyroradius (Bohm limit), the spectrum of accelerated electrons at the shock front is quite insensitive to the magnetic field strength $B_{\rm d}$ if all other relevant parameters are fixed; the exception is their maximal energy $\epsilon_{\rm max}^{\rm e}\propto V_{\rm s}B_{\rm d}^{-1/2}$ which is due to synchrotron losses (e.g. Berezhko & Völk 2004b). Since all energy of the electrons at high energies $\epsilon>\epsilon_{\rm l}\propto B_{\rm d}^{-2}$, where synchrotron losses are significant, is rapidly and completely transformed into the synchrotron emission, the same is true for the high frequency ( $\nu>\nu_{\rm l}\propto \epsilon_{\rm l}^2/B_{\rm d}$) part of the synchrotron spectrum including its cutoff part, because the cutoff frequency $\nu_{\rm max}\propto \epsilon_{\rm max}^{\rm e}B_{\rm d}^{1/2}$ does not depend on $B_{\rm d}$. (In the case B0=30 $\mu $G and $B_{\rm d}=150$ $\mu $G we have $\epsilon_{\rm max}^{\rm e}\approx 10^{14}$ eV and $\nu_{\rm max}\approx 10^{18}$ Hz.) However, varying the magnetic field strength $B_{\rm d}$ changes the amplitude of the overall calculated synchrotron spectrum at high frequencies $\nu>\nu_{\rm l}$ in order to keep the fit of the measured radio spectrum at low frequencies. Therefore the high frequency part of the spectrum $S_{\!\nu}$ changes due to the variation of the breaking frequency $\nu_{\rm l}\propto B_{\rm d}^{-3}$. Since below $\nu_{\rm l}$ the synchrotron spectrum has the form $S_{\nu}\propto \nu^{-\alpha}$ with $\alpha\approx 0.5$, we conclude that the high frequency part of the synchrotron spectrum depends on $B_{\rm d}$ as $\nu_{\rm l} S_{\!\nu}(\nu_{\rm l})\propto B_{\rm d}^{-3/2}$. The amplitude $\nu_{\rm l} S_{\!\nu}(\nu_{\rm l})$ is therefore the main determinant of the value of $B_{\rm d}$. Together with the observed synchrotron amplitude in the radio frequency region, where radiative losses play no role yet, the amplitude of the nonthermal electron distribution and thus the electron/proton ratio ratio $K_{\rm ep}$ also is determined. Note that the synchrotron spectrum is almost insensitive to the ISM density $N_{\rm H}$ (e.g. Ksenofontov et al. 2005).

 \begin{figure} \par\includegraphics[width=12cm,clip]{11948fg4.eps} \end{figure} Figure 4:

X-ray synchrotron emission flux as a function of photon energy for the same case as in Fig. 1 (solid line). Calculations for B0=27 $\mu $G ( dash-dotted line) and for B0=33 $\mu $G ( dashed line) are also presented. The observed X-ray flux from Chandra in red for a small region of the bright northeastern rim of SN 1006 (Allen et al. 2004), and the global X-ray spectrum in blue as observed by Suzaku (Bamba et al. 2008) are shown. The Chandra X-ray flux was normalized as to be consistent with the Suzaku flux for energies $\epsilon > 2$ keV.
Open with DEXTER

To obtain the fit to the data shown in Fig. 3 and Fig. 4, it is assumed that only the highest-energy part of the observed global X-ray spectrum, corresponding to $\epsilon > 2$ keV, is of predominantly nonthermal origin. Towards lower energies $\epsilon < 2$ keV, the contribution of thermal emission to this X-ray spectrum progressively increases, as clearly indicated by the Suzaku spectrum. For these considerations, the X-ray Chandra flux from a small region of the bright north eastern rim of SN 1006 (Allen et al. 2004) is used, where the contributions from thermal X-rays are presumably minimal (Cassam-Chenaï et al. 2008; Allen et al. 2004). In order to apply it to the whole remnant, this X-ray flux was normalized to be consistent at energies $\epsilon > 2$ keV with the global X-ray spectrum as observed by Suzaku (Bamba et al. 2008). This consistency in fact exists. For quantitative purposes, the normalised Chandra spectrum above 2 keV is used, under the assumption that it corresponds to pure nonthermal emission. Comparison with the experimental X-ray data shows in Figs. 3 and 4 that the optimum magnetic field value is B0=30 $\mu $G, and corresponds to a downstream field $B_{\rm d}\approx 150$ $\mu $G. This is in agreement with the field amplification that is implied by the filamentary structures in hard X-rays (Völk et al. 2005).

Figure 5 shows the contours of $\chi ^2$ characterizing the quality of fit of the radio spectrum, and of the X-ray spectrum for $\epsilon > 2$ keV, for different values of $\eta $ and $K_{\rm ep}$. One can see that the quality of the fit is rather good, allowing only a rather small range of these parameters.

The quality of fit of the radio spectrum, and of the X-ray spectra for $\epsilon > 2$ keV, for B0=30 $\mu $G is characterised by the value $\chi^2/{\rm dof} =1.3$. An increase $\Delta \chi^2 \approx 1$ of $\chi ^2$(see Fig. 4) implies a change of the magnetic field strength value by only 10%.

 \begin{figure} \par\includegraphics[width=8cm,clip]{11948fg5.eps} %\end{figure} Figure 5:

Contours of equal deviations $\Delta \chi ^2$(shown on the curves) from the minimum value of $\chi ^2$, in the plane that is spanned by the electron to proton ratio $K_{\rm ep}$ and the proton injection rate $\eta $. The asterisk corresponds to the best fit values $\eta = 3\times 10^{-4}$ and $K_{\rm ep} = 4\times 10^{-4}$ with the minimum value $\chi ^2/{\rm d.o.f.} = 1.3$. The fit uses jointly the radio and nonthermal X-ray data.
Open with DEXTER

The $\gamma $-ray  morphology, as found in the H.E.S.S. measurements (Naumann-Godo et al. 2009), is consistent with the prediction of a polar cap geometry by Völk et al. (2003). Such a geometry has been also found experimentally from an analysis of the synchrotron morphology in hard X-rays by Rothenflug et al. (2004) and Cassam-Chenaï et al. (2008). This means that the $\gamma $-ray  emission calculated in the spherically symmetric model must be renormalized (reduced) by a factor $f_{\rm re} \approx 0.2$, as in Ksenofontov et al. (2005). The renormalization factor is applied here.

This morphology is also the key argument for the existence of an energetically dominant nuclear CR component in SN 1006, because only such a component can amplify the magnetic field to the observed degree. If on the contrary the existing energetic electron component would have to drive the magnetic field amplification all by itself then we would, as a minimum, require $P_{\rm e}\gg B_0^2/(8\pi)$, where $P_{\rm e}$ is the pressure of CR electrons at the shock front. Clearly $P_{\rm e}~\raisebox{0.2em}{$<$ }\!\!\!\!\! \raisebox{-0.25em}{$\sim$ }~K_{\rm ep} P_{\rm p}$, where $P_{\rm p} \approx P_{\rm c}$ is the pressure of CR protons and $P_{\rm c}$ is the pressure of the nuclear component. Since $P_{\rm c}\approx 0.5\rho_0V_{\rm s}^2$ we have $P_{\rm e}\approx 0.07 B_0^2/(8\pi)$ for $N_{\rm H}=0.05~\mbox{cm}^{-3}$ and $V_{\rm s} \approx 4000$ km s-1. Therefore accelerated electrons are not able to amplify the magnetic field to the required level by a large margin. On the other hand, the effectively accelerated nuclear component has the pressure $P_{\rm c}\approx 200 B_0^2/(8\pi)$ and can therefore readily amplify the field from a purely energetic point of view.

The amplified field must also be the reason for the corresponding polar cap-type morphology of the synchrotron emission in hard X-rays. Even though the weak radio synchrotron emission, essentially all around the periphery of SN 1006 (Cassam-Chenaï et al. 2008; Rothenflug et al. 2004), demonstrates that electrons are at least to some extent injected everywhere into the acceleration process over the shock, they reach the multi-TeV energies for X-ray synchrotron emission only in the polar caps, where the amplified field allows their acceleration to these energies. In the equatorial region the upstream magnetic field strength corresponds to its ISM value, at the height of SN 1006 above the Galactic plane probably not more than $3 \mu$G. Particle scattering is comparatively weak and the maximum electron energy is expected to lie below the limit where the acceleration rate equals the synchrotron loss rate. Then the maximum electron energy is - like that of the nuclear particles - determined by the system geometry (Berezhko 1996); an explicit calculation can be found in Berezhko & Völk (2004b). Assuming then for simplicity that the spatial diffusion coefficient has the form $\kappa = \delta \cdot \kappa_{\rm Bohm}$, with a constant factor $\delta > 1$, requires $\delta > 4$ even for this low field strength in order to reduce the equatorial maximum synchrotron frequency $\nu_{\rm max}$ to $\nu_{\rm max} < 10^{17}$ Hz, for an azimuthally uniform shock velocity $V_{\rm s} \approx 4000$ km s-1. Such a plausible reduction of $\nu_{\rm max}$ is consistent with the findings of Rothenflug et al. (2004); see also Miceli et al. (2009).

The only important parameter that cannot be determined from the analysis of the synchrotron emission data is the external density $N_{\rm H}$. Therefore we have performed the calculations for the pair of values $N_{\rm H}=0.05~\mbox{cm}^{-3}$ and $N_{\rm H}=0.035~\mbox{cm}^{-3}$ which seems to bracket the density range consistent with the H.E.S.S. $\gamma $-ray  measurements.

Figure 6 shows the total ($\pi ^0$-decay plus inverse Compton (IC)), and seperately the $\pi ^0$-decay and the IC $\gamma $-ray energy spectra of the remnant, calculated for $N_{\rm H}=0.05~\mbox{cm}^{-3}$ and $N_{\rm H}=0.035~\mbox{cm}^{-3}$.

H.E.S.S. has reported the measured value of the energy flux $\Phi (\epsilon_1, \epsilon_2)=2.5\times 10^{-12}$ erg/(cm2 s) of $\gamma $-rays  with energies $\epsilon_1 \le \epsilon_{\gamma}\le \epsilon_2$, where $\epsilon_1 = 0.2$ TeV and $\epsilon_2 = 40$ TeV. It is related to the differential $\gamma $-ray  energy spectrum according to the expression

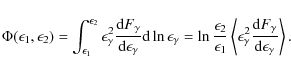
\begin{displaymath}\Phi(\epsilon_1, \epsilon_2)= \int_{\epsilon_1}^{ \epsilon_2}... ...rac{{\rm d}F_{\gamma}}{{\rm d}\epsilon_{\gamma}}\right\rangle. \end{displaymath}

In a selfconsistent picture, the theoretically predicted form of the differential spectrum d $F_{\gamma}$/d $\epsilon_{\gamma}$, cf. Fig. 6 is used to calculate the mean experimental value of the differential energy flux $\langle\epsilon_{\gamma}^2 {\rm d}F_{\gamma}/{{\rm d}\epsilon_{\gamma}}\rangle= \Phi(\epsilon_1, \epsilon_2)/\ln(\epsilon_2/\epsilon_1)$, shown in Fig. 6.

Note that the peak in the $\gamma $-ray energy spectrum at $\epsilon_{\gamma} \approx 5$ TeV and the quasi-exponential cutoff at higher energies is due to the substantial contribution of the IC component: at TeV energies the IC component contributes about half of the total $\gamma $-ray  flux for $N_{\rm H}=0.05~\mbox{cm}^{-3}$, whereas for $N_{\rm H}=0.035~\mbox{cm}^{-3}$ it is already two thirds. Since the maximal proton energy, reached at some time during the evolution, is about $\epsilon_{\rm max}\approx 2\times 10^{15}$ eV, the corresponding $\pi ^0$-decay component has a power law form ${\rm d}F_{\gamma}/{\rm d}\epsilon_{\gamma}\propto \epsilon_{\gamma}^{-\gamma}$ with $\gamma\sim 2$ up to the cutoff energy $\epsilon_{\gamma}\approx 10^{14}$ eV. The cutoff energy is defined here as that energy where the spectral energy density has dropped by a factor 1/e from its maximum value, which is given by log $\epsilon_{\gamma}^2 {\rm d}F_{\gamma}/{{\rm d}\epsilon_{\gamma}} \approx -0.8$.

 \begin{figure} \par\includegraphics[width=9cm,clip]{11948fg6.eps} \end{figure} Figure 6:

Total ($\pi ^0$-decay + IC) ( black lines), $\pi ^0$-decay ( blue lines), and IC ( green lines) differential $\gamma $-ray energy fluxes as a function of $\gamma $-ray energy, calculated for ISM hydrogen number densities $N_{\rm H}=0.05~\mbox{cm}^{-3}$ ( solid lines) and $N_{\rm H}=0.035~\mbox{cm}^{-3}$ ( dashed lines) for the parameters $\eta =2.9\times 10^{-4}$, $K_{\rm ep}= 4.1\times 10^{-4}$ and $B_{\rm d}=150$ $\mu $G, derived from the fit of the synchrotron spectrum. The H.E.S.S. value (Naumann-Godo et al. 2009) is shown as well.
Open with DEXTER

According to Fig. 6, the H.E.S.S. data are consistent with an ISM number density from quite a narrow interval $0.035\le N_{\rm H}\le 0.05~\mbox{cm}^{-3}$, since for the theoretically derived $\gamma $-ray  spectrum we have $\Phi=2.1\times 10^{-12}$ erg/(cm2 s) and $\Phi=2.9\times 10^{-12}$ erg/(cm2 s) for $N_{\rm H}=0.035~\mbox{cm}^{-3}$ and $N_{\rm H}=0.05~\mbox{cm}^{-3}$ respectively. The corresponding explosion energy $E_{\rm sn}\approx 1.7\times 10^{51}$ erg is close to the upper end of the typical range of type Ia SN explosion energies that vary by a factor of about two (Blinnikov et al. 2006; Gamezo et al. 2005).

Acero et al. (2007) find the value $N_{\rm H}\approx 0.05~\mbox{cm}^{-3}$ on the basis of X-ray measurements. The above interval is consistent with their result.

In Figure 6, the $\gamma $-ray  spectrum produced by the nuclear CRs is very close to the IC emission spectrum produced by CR electrons alone. Since the differential energy spectrum of freshly accelerated nuclear particles and electrons is rather close to a spectrum $N_{\rm e}\propto \epsilon^{-2}$, and since the electrons with energies $\epsilon>\epsilon_{\rm l}\approx 1$ TeV subsequently undergo significant synchrotron cooling in the interior, leading to the spectrum $N_{\rm e}\propto \epsilon^{-3}$, not only the amplitude but also the shape of these two components are very similar within the energy interval $10^{10}<\epsilon_{\gamma}<10^{13}$ eV. Therefore the VHE $\gamma $-ray  spectrum alone is not able to discriminate between the hadronic $\pi ^0$-decay and the leptonic IC $\gamma $-ray  components. However, it was already shown by Ksenofontov et al. (2005) that such a low VHE emission flux, with a highly depressed IC $\gamma $-ray  flux, is only possible if the nuclear CR component is efficiently produced with accompanying strong magnetic field amplification. In the framework of the interpretation developed in this paper, the most direct evidence for the energetic dominance of a nuclear energetic particle component is the observed $\gamma $-ray  morphology. It corresponds to the theoretical prediction and is consistent with all other measurements.

A last point concerns the radial extent $R_{\rm c}$ of the contact discontinuity between ejected and swept-up mass relative to the radius $R_{\rm s}$ of the SNR blast wave, cf. recent data presented and discussed by Cassam-Chenaï et al. (2008). The ratio $R_{\rm s}/R_{\rm c}$ is given as $1.04 \pm 0.03$ outside the synchrotron rims, and essentially as 1 in the region within the synchrotron rims. In the case of Tycho's SNR we have discussed in quantitative detail (e.g. Völk et al. 2008a) the reduction of this ratio compared to a pure gas shock as a result of the considerable shock modification produced by accelerated nuclear CRs, which leads to the increase of the shock compression. Qualitatively such considerations agree with the experiment for SN 1006: the ratio $R_{\rm s}/R_{\rm c}$ is larger in the equatorial region, where CR injection/acceleration is inefficient, and it is smaller within the polar region, where CRs are efficiently produced. While for Tycho's SNR particle acceleration gives a good theoretical explanation of the relatively small ratio within our model, this is clearly impossible quantitatively for the above numbers in the case of SN 1006. Cassam-Chenaï et al. (2008) believe that the value of the contact discontinuity radius $R_{\rm c}$ was overestimated ``... since our measurements are likely to be affected by projection and other effects, ...''. On the other hand, very recently Miceli et al. (2009) have found $R_{\rm s}/R_{\rm c}$ of the order of 1.1, which is in the expected range. Future work will have to resolve this difference.

3 Summary

Since the relevant astronomical parameters as well as the synchrotron spectrum of SN 1006 are measured in impressive detail, it is possible to determine the values of the relevant physical parameters with the appropriate accuracy for this SNR: the proton injection rate $\eta=(2.9\pm 0.6)\times 10^{-4}$, the electron to proton ratio $K_{\rm ep}= (4.1\pm 0.3)\times 10^{-4}$, and the downstream magnetic field strength $B_{\rm d}=(150\pm 15)$ $\mu $G.

As a result, the flux of TeV emission detected by H.E.S.S. is consistent with the ISM number density $0.035\le N_{\rm H}\le 0.05~\mbox{cm}^{-3}$. The corresponding hydrodynamic SN explosion energy $E_{\rm sn}= 1.7\times 10^{51}$ erg is close to the upper end $E_{\rm sn}= 1.6 \times 10^{51}$ erg of the typical range of type Ia SN explosion energies that vary by a factor of about two. Also the magnetic field amplification properties of this SNR are well understandable as the result of azimuthal variations of ion injection over the projected SNR circumference and corresponding acceleration which lead to a polar cap-type morphology for the X-ray synchrotron as well as the $\gamma $-ray  emission. As a consequence, the recent H.E.S.S. measurement of a dipolar morphology also of the TeV $\gamma $-ray  emission is considered as the most significant empirical evidence for the existence of an energetically dominant nonthermal nuclear component.

Thus, SN 1006 appears to represent the first example where a high efficiency of nuclear CR production, required for the Galactic CR sources, is consistently established.

Acknowledgements
This work has been supported in part by the Russian Foundation for Basic Research (grants 06-02-96008, 07-02-0221). The authors are grateful to Drs. Aya Bamba and Glen Allen who provided them with the most recent X-ray data from the Chandra and Suzaku satellite observatories. The authors also thank Dr. Vladimir Zirakashvili for discussions regarding electron acceleration in SN 1006. EGB acknowledges the hospitality of the Max-Planck-Institut für Kernphysik, where part of this work was carried out.

Appendix A

The relation between the model calculations in spherical symmetry (1D) and the physical characteristics of the system in the presence of a symmetry-breaking magnetic field in the circumstellar medium were discussed earlier (Völk et al. 2003). In order to clarify the necessary corrections to the 1D-calculation for SN 1006, a qualitative discussion of the physical situation is given here.

A key feature is the empirical fact that the force density of the magnetic field in the diffusive shock acceleration process can be neglected compared to the gas ram pressure, the thermal pressure and the CR pressure. The average magnetic field configuration can thus in principle be calculated purely kinematically from the induction equation. However, the magnetic field direction influences the injection at least of heavy ions in a significant way. In a quasi-parallel shock, where the angle $\Theta_{\rm nB}$ between the local mean field and the shock normal is small compared to $90^{\circ}$, the required velocity of suprathermal ions from the downstream region, required to be able to cross the shock into the upstream region, is much smaller than in a quasi-perpendicular shock, where $\Theta_{\rm nB}$ is close to $90^{\circ}$. For a steeply falling velocity distribution of the shocked downstream gas, this leads to effective suppression of ion injection in quasi-perpendicular shocks (Malkov & Völk 1995; Ellison et al. 1995). The acceleration of injected particles, on the other hand, is efficient for all $\Theta_{\rm nB}$ for non-relativistic shocks, as long as $\cos \Theta_{\rm nB} \gg V_{\rm s}/c$, where $V_{\rm s}$ and c denote the shock velocity and the speed of light, respectively (Drury 1983). The injection of electrons is not yet well understood. From the observed azimuthal distribution of the radio synchrotron emission in SN 1006 (e.g. Cassam-Chenaï et al. 2008), electron injection seems to operate for all angles $\Theta_{\rm nb}$, although apparently less efficiently in the quasi-perpendicular region. This is the least restrictive assumption and it is made here in the sequel.

A second point is that in the instantaneously quasi-parallel part of the magnetic flux tubes in which ions are injected, the accelerated particles drive a current against the flow of the upstream gas that generates strong magnetic fluctuations and amplifies the magnetic field, as referred to in the main text. This enhances the acceleration and leads to a pressure $P_{\rm c}$ of the energetic nuclear particles that is comparable to the gas ram pressure for strong shocks, e.g. in young SNRs, as well as to heating of the gas by wave dissipation, both of the non-resonant and of the resonant Alfvénic modes (McKenzie & Völk 1982; Pelletier et al. 2006; Zirakashvili et al. 2008; Bell & Lucek 2001; Bell 2004; Lucek & Bell 2000). Especially the formation of density fluctuations and corresponding secondary shocks is viewed here as a reason for strong wave dissipation (Völk et al. 2008a; Berezhko 2008). The pressure of accelerated electrons is negligible in comparison. This implies a strong hadronic $\gamma $-ray  emission from that part of these flux tubes, which at some time became quasi-parallel. This hadronic flux is negligible elsewhere because there are few energetic nuclei there. A certain amount of cross-field diffusion will, however, also populate neighboring flux tubes and somewhat smear out the acceleration boundaries (Völk et al. 2003). Accelerated electrons will emit strong synchrotron radiation in the enhanced magnetic field regions, but may also yield a more moderate synchrotron flux elsewhere. The reason is that by assumption they are injected and accelerated to some extent ``everywhere'' on the shock surface, albeit to considerably lower maximum energies in the quasi-perpendicular regions. This is the result of the lack of self-excited magnetic field fluctuations and of field amplification (see Sect. 2).

The third point regards differences in overall dynamics of the quasi-parallel and quasi-perpendicular regions. Conservation of the overall mass, momentum and energy fluxes allows only a different partition within the momentum and energy fluxes between their kinetic, thermal and nonthermal components, but the sums of these fluxes always remain the same. However, the compressibility of the relativistic CR ``gas'' is higher than that of the nonrelativistic thermal gas, and therefore this different partition implies dynamical differences between the quasi-parallel and the quasi-perpendicular regions.

When primarily the cumulative effect of the higher compressibility counts, such as in the relative distance between the outer SNR blast wave and the following contact discontinuity, then the different partitions in a CR-modified shock and a pure gas shock play the determining role.

However, in the present context, where the main characteristics of the radiation effects and of their spatial distributions are to be evaluated, such dynamical differences can to a first approximation be neglected. In practice, for SN 1006, the overall shock compression ratio changes from $\sigma = 4$without CR production to $\sigma \sim 5$ with efficient CR production, given the assumed strong gas heating in the shock precursor.

Thus, for the evaluation of the hadronic $\gamma $-ray  emission, only those flux tubes from the 1D gas dynamic configuration are considered, which connect to the part of the present phase shock surface where ion injection is efficient. This requires the correction factor $f_{\rm re}<1$. Since the particle transport perpendicular to the magnetic field direction is primarily corrective, adiabatic expansion of the thermal gas leads to adiabatic losses of the energetic particles and weakens the interior particle distribution. In addition, almost all flux tubes originally have been quasi-perpendicular. The corresponding parts of these flux tubes are now in the deeper interior of the SNR and therefore, to a first approximation, lack accelerated nuclei there. For electrons the radiative losses also increase towards the interior where the ``older'' particles reside. These arguments show that both the synchrotron and the $\gamma $-ray  emission are concentrated near the shock surface rather than in the interior. As long as the ejected mass is not negligible compared to the swept-up mass, the ejecta volume in the interior with its extremely small magnetic field strength will appear as a region with particularly little radiation. For SN 1006 with its supposedly simple magnetic field geometry, the evaluation of the ion injection fraction $f_{\rm re}$ of the shock surface has been given by Völk et al. (2003).

The electron spectrum also is calculated in spherical symmetry from Eq. (3) of Berezhko et al. (2002). However, the actual evolutionary phase of SN 1006 appears to be still rather in the transition from the sweep-up phase to what one can loosely call a Sedov phase. Being pushed away by the ejecta, the density of the shocked circumstellar medium has remained rather uniform. In the quasi-parallel flux tubes, downstream of the shock, with massively injected nuclear particles, the field $B_{\rm d}$ should therefore be strong and roughly uniform if field dissipation is negligible. In the quasi-perpendicular regions on the other hand, the field is only about four times larger than in the ambient circumstellar medium. Finally, in the ejecta mass, the magnetic field strength is presumably very small at the present time. Taken together, the overall magnetic field strength in the SNR is far from uniform. Yet what counts primarily for the integrated synchrotron emission are the quasi-parallel regions.

It had indeed been assumed in past work (Ksenofontov et al. 2005; Berezhko et al. 2002) that to a first approximation only those magnetic flux tubes play a role in the spatially integrated emission that end at the forward shock in the polar caps. Therefore this integral already contains the correction factor $f_{\rm re}$implicitly and can be directly compared to the observed integral flux. The key consideration in all of this is that the SNR consists of a strongly CR-modified part with strong magnetic field amplification and a part that is essentially unmodified. The correction factor changes only the amplitude but not the form of the calculated spectrum.

Adding a small population of electrons accelerated in the unmodified shock of the quasi-perpendicular regions would smear out the specifically nonlinear properties of the synchrotron spectrum. Therefore, the observed synchrotron spectrum exhibits the minimum nonlinear modifications which in reality should be even stronger. This means that the derived ion injection rate, magnetic field amplification and electron/proton ratio are lower limits for the quasi-parallel regions.

References

Footnotes

...)[*]
These papers contain the basic equations used, in the form of a transport equation for energetic charged particles in a shock environment and its coupling to the gas dynamical equations for the thermal plasma. Considering seperately the energetic electron component, a corresponding transport equation is added that includes radiative energy losses (Berezhko et al. 2002). Also the particles' diffusion properties in the form of the Bohm limit, wherever nuclear particles are effectively injected into strong shocks, as well as the assumed heating rate of the thermal plasma by wave dissipation are detailed in these papers.

All Figures

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{11948fg1.eps} \end{figure} Figure 1:

Gas dynamical evolution for the two values of the total explosion energy $E_{\rm sn}= 1.8\times 10^{51}$ erg and $E_{\rm sn}= 1.5\times 10^{51}$ that correspond to the values $N_{\rm H}=0.05~\mbox{cm}^{-3}$ and $N_{\rm H}=0.035~\mbox{cm}^{-3}$ of the ISM hydrogen number density, respectively. The quantities $R_{\rm s}$ and $V_{\rm s}$ denote the shock radius and the shock velocity, their time evolution being fitted to the observed values shown. The vertical dotted line indicates the present epoch.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11948fg2.eps} \end{figure} Figure 2:

Overall (=spatially integrated) spectra of energetic particles. Solid and dashed lines correspond to protons (p) and electrons (e), respectively.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11948fg3.eps} \end{figure} Figure 3:

Differential synchrotron radio emission flux as a function of frequency, calculated for the ISM hydrogen number density $N_{\rm H}=0.05~\mbox{cm}^{-3}$ at the proton injection rate $\eta = 3\times 10^{-4}$, electron to proton ratio, $K_{\rm ep} = 4\times 10^{-4}$, and magnetic field strength B0=30 $\mu $G upstream of the subshock . The observed radio emission flux from a compilation of Allen et al. (2004) (see also Allen et al. 2008,2001) is shown.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=12cm,clip]{11948fg4.eps} \end{figure} Figure 4:

X-ray synchrotron emission flux as a function of photon energy for the same case as in Fig. 1 (solid line). Calculations for B0=27 $\mu $G ( dash-dotted line) and for B0=33 $\mu $G ( dashed line) are also presented. The observed X-ray flux from Chandra in red for a small region of the bright northeastern rim of SN 1006 (Allen et al. 2004), and the global X-ray spectrum in blue as observed by Suzaku (Bamba et al. 2008) are shown. The Chandra X-ray flux was normalized as to be consistent with the Suzaku flux for energies $\epsilon > 2$ keV.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm,clip]{11948fg5.eps} %\end{figure} Figure 5:

Contours of equal deviations $\Delta \chi ^2$(shown on the curves) from the minimum value of $\chi ^2$, in the plane that is spanned by the electron to proton ratio $K_{\rm ep}$ and the proton injection rate $\eta $. The asterisk corresponds to the best fit values $\eta = 3\times 10^{-4}$ and $K_{\rm ep} = 4\times 10^{-4}$ with the minimum value $\chi ^2/{\rm d.o.f.} = 1.3$. The fit uses jointly the radio and nonthermal X-ray data.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm,clip]{11948fg6.eps} \end{figure} Figure 6:

Total ($\pi ^0$-decay + IC) ( black lines), $\pi ^0$-decay ( blue lines), and IC ( green lines) differential $\gamma $-ray energy fluxes as a function of $\gamma $-ray energy, calculated for ISM hydrogen number densities $N_{\rm H}=0.05~\mbox{cm}^{-3}$ ( solid lines) and $N_{\rm H}=0.035~\mbox{cm}^{-3}$ ( dashed lines) for the parameters $\eta =2.9\times 10^{-4}$, $K_{\rm ep}= 4.1\times 10^{-4}$ and $B_{\rm d}=150$ $\mu $G, derived from the fit of the synchrotron spectrum. The H.E.S.S. value (Naumann-Godo et al. 2009) is shown as well.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.