EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 499 / No 1 (May III 2009) A&A, 499 1 (2009) 331-335 Full HTML
Free Access
Issue
A&A
Volume 499, Number 1, May III 2009
Page(s) 331 - 335
Section Celestial mechanics and astrometry
DOI https://doi.org/10.1051/0004-6361/200911714
Published online 01 April 2009

Determining the relativistic parameter 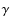$\gamma $ using very long baseline interferometry

S. B. Lambert - C. Le Poncin-Lafitte

Observatoire de Paris, Département Systèmes de Référence Temps Espace (SYRTE), CNRS/UMR 8630, 75014 Paris, France

Received 23 January 2009 / Accepted 8 March 2009

Abstract
Aims. Relativistic bending in the vicinity of a massive body is characterized only by the post-Newtonian parameter $\gamma $ within the standard parameterized post-Newtonian formalism, which is unity in General Relativity. To estimate this parameter, we use very long baseline interferometry (VLBI) to measure the gravitational deflection of radio waves by Solar System bodies emitted by distant compact radio sources.
Methods. We analyze geodetic VLBI observations recorded since 1979. We compare estimates of $\gamma $ and errors obtained with various analysis schemes, including global estimations over several time spans and with various Sun elongation cut-off angles, and with analysis of radio source coordinate time series.
Results. We arrive at the conclusion that the relativistic parameter $\gamma $ cannot be estimated at better than $2\times10^{-4}$. The main factor of limitation is the uncertainty in determining of (global or session-wise) radio source coordinates. A sum of various instrumental and modeling errors and analysis strategy defects, which cannot be decorrelated and corrected yet, is at the origin of the limitating noise.

Key words: astrometry - relativity - techniques: interferometric

1 Introduction

One of the cornerstones of test of general relativity (GR) is the measurement of light deflection in the vicinity of the Sun. In the parameterized post-Newtonian (PPN) formalism (Will 1993), which contains 10 parameters, the predicted angle of deflection $\theta$ is

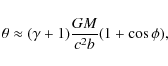\begin{displaymath}\theta\approx(\gamma+1)\frac{GM}{c^2b}(1+\cos\phi), \end{displaymath} (1)

where G is the Newtonian gravitational constant, c the speed of light in a vacuum, M the mass of the deflecting body, b the impact parameter (defined as the minimal distance of the ray to the center of mass of the deflecting body), $\phi $ the elongation angle between the deflecting body and the source as viewed by the observer, and $\gamma $ is the PPN parameter characterizing the space curvature due to gravity. (See, e.g., Misner et al. 1973; Will 1993; and more generally speaking for an axisymmetric body, Le Poncin-Lafitte & Teyssandier 2008.) Thus, a grazing ray at the Sun's limb is deflected by $\sim$1.7 $^{\prime\prime}$. In GR $\gamma=1$. It is crucial that light deflection experiments give us privileged access to $\gamma $, independent of other post-Newtonian parameters. This point is even more important when one thinks that cosmological models (Damour & Polyakov 1994; Damour et al. 2002) predict deviations of $\vert\gamma-1\vert$ of the order of 10-6-10-7.

Very long baseline radio interferometry (VLBI) is sensitive to space-time curvature through the gravitational time delay, given by (e.g., Finkelstein et al. 1983)

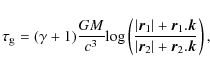\begin{displaymath}\tau_{\rm g}=(\gamma+1)\frac{GM}{c^3}{\rm log}\left(\frac{\ve... ...t+\vec r_1.\vec k}{\vert\vec r_2\vert+\vec r_2.\vec k}\right), \end{displaymath} (2)

where $\vec r_i$ stands for the position vector of the ith station and $\vec k$ the unit vector pointing towards the radio source, both referring to the center of mass of the deflecting body. For a typical VLBI baseline between Westford (Massachusetts) and Wettzell (Germany) of $\sim$6000 km, $\tau _{\rm g}$ is $\sim$170 nanoseconds (ns) for a source at the Sun's limb, rapidly decreases to $\sim$10 ns at 4$^{\circ }$ away from the Sun, and remains close to the accuracy of VLBI measurements (nowadays around 10 ps), even for elongations close to 180$^{\circ }$ (see Fig. 1).

 \begin{figure} \par\includegraphics[width=9cm]{1714fig1.eps}\end{figure} Figure 1:

Gravitational delay $\tau _{\rm g}$ as a function of the elongation angle $\phi $ to the Sun for the baseline Westford-Wettzell.
Open with DEXTER

VLBI has been used on a regular basis since the early 1980s for monitoring Earth orientation and estimating station displacements and extragalactic radio source coordinates at 2 and 8 GHz. The number of radio sources per session, as well as the data recording reliability, have drastically improved in the past decade. About 4000 diurnal session files, representing more than 5 million delays, are made available through the International VLBI Service for Geodesy and Astrometry (IVS, Schlüter & Behrend 2007) data base.

The large amount of data from the permanent geodetic VLBI program can provide a number of tests of GR (Soffel et al. 1986). In the past years, VLBI data were used in various attempts to determine $\gamma $. Using less than 4 years of observations, Robertson & Carter (1984) found $\gamma $ consistent with GR within 0.005. Using 10 years of observations, Robertson et al. (1991) estimated a standard error of 0.002. Lebach et al. (1995) got $0.9996\pm0.0017$ after observations of the relative deflection of 3C 273B and 3C 279. Shapiro et al. (2004) obtained $0.99983\pm0.00026$ (statistical standard error) with VLBI observations before 1999. The current best estimate of $\gamma $, however, was not obtained with VLBI: it is consistent with GR with an error of  $2\times 10^{-5}$, and was obtained by Bertotti et al. (2005) who derived it from spacecraft tracking experiments.

Errors reported in the various papers are often formal errors obtained from the propagation through the adjustment procedure of an initial SNR-derived standard error on the delays. They might therefore not directly compare to one another. Though all these works (except Bertotti et al.) deal with deflection of the radio waves by the Sun, it must be mentioned that special VLBI sessions were carried out to measure the deflection close to Jupiter or other planets (Schuh et al. 1988).

In this work, we estimate $\gamma $ from routine geodetic VLBI observations, using the additional 1999-2008 time period with respect to Shapiro et al. We compare estimates and errors obtained over several time spans and using various analysis schemes in order to address the accuracy and to point out some systematics and limitations.

 \begin{figure} \par\includegraphics[width=9cm]{1714fig2.eps}\end{figure} Figure 2:

Observational history of the sources at less than 30$^{\circ }$ to the Sun. The upper plot gives the Sun spot number (SSN, Clette et al. 2007). The right plot displays the deflection angle as predicted by GR.
Open with DEXTER

2 Close approaches to the Sun

A set of 3937 24-h geodetic VLBI sessions, consisting of about 4.5 million delays, will be fully or partly processed in the upcoming analyses. During the period that covers 3 August 1979-28 August 2008, the VLBI observing schedule included a number of radio sources that were observed at less than 15$^{\circ }$ to the Sun. As it shows up in Fig. 2, this number was weak before 1984, quite uniform during 1984-1996. Then it increased substantially during 1996-2002. It is worth noting that 1992-1999, which contains a number of close approaches, is a period of low solar activity. Since 2002, the scheduling software at the IVS coordinating center was set with a minimal distance to the Sun at 15$^{\circ }$. Figure 2 naturally yields several time spans on which the analyses can be done: 1979-2008, which is the maximum number of available data; 1984-2008, which drops the early VLBI network; 1996-2002, which shows the highest density of close approaches; and 1984-2002, which represents a compromise between a high density of close approaches and a large amount of data. Additionally, we also consider 1979-1999, as in Shapiro et al., in order to check that we are consistent with their results. Finally, we would like to address two time spans that cover periods of low and high solar activity. It is nevertheless difficult to keep the same characteristics (number of sessions, number of sources, density of close approaches) for these two periods since the VLBI observing program undergoes continuous evolution. We propose the three following time spans: 1994-1997, 1998-2002a (started 01/1998, and has approximately the same number of sessions and sources as 1994-1997), and 1998-2002b (started 07/1998, and has approximately the same number of delays as 1994-1997).

All our VLBI delays were corrected from delay due to the radio wave crossing of dispersive region in the signal propagation path in a preliminary step that made use of 2 GHz and 8 GHz recordings. Then, we only used the 8 GHz delays to fit the parameters listed in the next section. In the case of targets that are close to the Sun, the relevant dispersive regions are the Earth's ionosphere and the solar coronal plasma. Although approximated, the model for plasma delay correction as a function of electronic content and frequency should lead to errors of a few picoseconds, following Lebach et al. (1995). (The authors mentioned this magnitude for a period of low solar activity. During periods of higher activity, the electronic content can be several times higher.) The reader must therefore keep in mind this order of magnitude when potential sources of limitation are listed in later sections. Likewise, an error in the solar coronal plasma delay correction would lead to a falsified estimate of $\gamma $, since the plasma-induced deflection would be absorbed there. Rather than a relativistic parameter, $\gamma $ would therefore be simply considered as a ``deflection'' parameter.

Table 1:   Characteristics of the solutions and estimates of $\gamma $.

3 Data analysis and results

3.1 Global solutions

We run global solutions over these time spans. In all these solutions, the Earth orientation parameters and the station coordinates are estimated once per session, and $\gamma $ is estimated as a global parameter. Source coordinates are also estimated as global parameters without global constraint: the sources are allowed to stay within circles of 10-8 rad diameter around a priori positions. The choice of the a priori catalogue for source coordinates is discussed later.

Now, we quickly go into some technical characteristics of the solutions. The cut-off elevation angle is set to 5$^{\circ }$. A priori zenith delays are determined from local pressure values (Saastamoinen 1972), which are then mapped to the elevation of the observation using the Niell mapping function (Niell 1996). Zenith wet delays are estimated as a continuous piecewise linear function at 20-min interval. Troposphere gradients are estimated as 8-h east and north piecewise functions at all stations except a set of 110 stations having poor observational history. Station heights are corrected from atmospheric pressure and oceanic tidal loading. The relevant loading quantities are deduced from surface pressure grids from the US NCEP/NCAR reanalysis project atmospheric global circulation model (Kalnay et al. 1996) and from the GOT00.2 ocean tide model (Ray 1999; Petrov & Boy 2004). No-net rotation constraint per session is applied to the positions of all stations, excluding HRAS 085 (Fort Davis, Texas) and Fairbanks (Alaska) because of strong non-linear displacements. (The latter site underwent post-seismic relaxation effects after a large earthquake on the Denali fault in 2003, cf. MacMillan & Cohen 2004; Titov & Tregoning 2004, 2005.) All the calculations use the Calc 10.0/Solve 2006.06.08 geodetic VLBI analysis software package and are carried out at the Paris Observatory IVS Analysis Center (Gontier et al. 2008). Results are reported in Table 1.

 \begin{figure} \par\includegraphics[width=8cm]{1714fig3.eps}\includegraphics[width=8cm]{1714fig4.eps}\end{figure} Figure 3:

Estimates of $\gamma $ for various cut-off of the Sun elongation angle. Horizontal, dashed lines figure $\pm \sigma $.
Open with DEXTER

Since source coordinates are estimated during the analysis process, the influence of the a priori catalogue on $\gamma $ is expected to be negligible. To check this, we ran the previous solutions several times, using several a priori catalogues. All of them were obtained after a global inversion of data over 1984-2008, wherein the celestial reference frame was maintained by applying a no-net rotation constraint on the coordinates on a well-chosen subset of sources that defines the axes of the International Celestial Reference System (ICRS, Feissel & Mignard 1997). Several subsets achieve this goal (Ma et al. 1998; Feissel-Vernier 2003; Feissel-Vernier et al. 2006; Lambert & Gontier 2009), and insure an alignment of the output catalogue onto the ICRS within 0.05 mas. (The latter nevertheless decreases this value below 0.02 mas.) It finally appeared that the sensitivity of estimated $\gamma $ to the chosen set of defining sources and to the a priori catalogue is at the level of 10-8, which is not statistically significant.

We wondered whether the fit could be improved by removing data from sources having a poor observational history (e.g., less than 2 observations or observed in less than 3 sessions). We therefore ran all the above solutions one more time after having downgraded about 200 sources as session parameters and suppressed the delays from another 100. The final post-fit root mean square (rms) and normalized reduced $\chi^2$ per degree of freedom ($\chi^2/f$) were not changed significantly. (The $\chi^2/f$ is output by the VLBI analysis software and reflects the goodness of the fit of the solution, including all adjusted parameters.) The influence on $\gamma $ estimates was only noticed at the level of 10-6, which appears to be non statistically significant, following the standard errors reported in Table 1.

The post-fit rms delay of the solutions ranges from 25-28 ps, Such an rms corresponds to a rough expected accuracy of 0.27 mas in terms of individual source positioning. One can readily see that, assuming such a measurement error on the direction of a grazing ray, one can expect an error $\delta\gamma$ not lower than $\delta\gamma/\gamma\simeq\delta\theta/\theta\simeq1.5\times10^{-4}$. This is confirmed by the standard errors reported in Table 1.

 \begin{figure} \par\includegraphics[width=7.8cm]{1714fig5.eps}\includegraphics[width=7.8cm]{1714fig6.eps}\end{figure} Figure 4:

(Left) Session-wise coordinates of 0229+131. (Right) Least-squares spectrum.
Open with DEXTER

The solutions over 1979-1999, 1979-2008, 1984-2002, and 1984-2008, which include a large number of sessions and delays and which all have $\chi^2/f$ larger than 0.86, all result in estimates of $\gamma $ consistent with GR within $\sigma=2\times10^{-4}$. Using the sessions after 2002 or before 1979, which do not contain close approaches below 15$^{\circ }$, makes the estimate of $\gamma $ depart from unity at the level of $1\sigma$. Incidentally, the solution over 1979-1999 confirms the analysis of Shapiro et al. with a slightly lower formal error that may originate from a different analysis strategy and a different observational data set.

Although they have a similar number of observations or sessions, solutions over 1998-2002(a,b) bring a substantially higher standard error than 1994-1998. Moreover, for 1994-1998, estimate of $\gamma $ appears to be lower than 1, whereas it is larger for 1998-2002(a,b). It indicates that the bending of sources is higher in the second case. Intense solar activity during this period could be at the origin of the discrepancy: during periods of high activity, the higher electronic content results in a higher deflection of radio waves. The absence in the software of a specific modeling of solar plasma effects and the strong correlation of an uncorrected plasma-induced bending with the relativistic deflection prevent these two phenomena from being separated.

3.2 Dependence on the elongation angle

To address the problem of the elongation angle to the Sun, we ran several solutions with an increasing cut-off angle, removing sources below successive thresholds up to 40$^{\circ }$. We applied this analysis scheme over several time spans (Fig. 3). For 1984-2002, a substantial degradation of the estimates occurs beyond 25$^{\circ }$, in agreement with similar tests in Shapiro et al. A bump reaches a maximum around 60$^{\circ }$ and then estimates of $\gamma $ approach unity. We ran a similar analysis over 2000-2008 because it constitutes a data set decorrelated from the one used by Shapiro et al. (allowing for the fact that (i) a part of the observed sources and observing antennas are the same in both data sets, (ii) the latter contains substantially less sessions than the former). The bump also shows up when using this data set.

We also checked what happens at short elongation angles over 1984-2002, 1994-1998, and 1998-2002. Below 25$^{\circ }$, the deviation from unity stays within the error bars with non statistically significant variations. For shorter solutions, estimates rapidly degrade beyond an elongation cut-off of a few degrees. For 1994-1998 and 1998-2002, the degradation occurs in opposite directions. Estimates of $\gamma $ appear to be lower than 1 in the former case, while they are larger in the latter, consistently with the global estimates of $\gamma $ over the same time periods shown in Table 1. The possible reason of such differences has already been addressed.

  3.3 Approach based on radio source coordinate time series

Estimating session-wise coordinates of sources can also be a way of looking at a possible deflection when the sources travel in the vicinity of the Sun. An uncorrected bending should appear as an annual signal in coordinate time series.

Among the observed sources, only two have close approaches below 2$^{\circ }$ and are observed in more than 500 sessions. Both cases are similar, but we only treat the source that has the longest observational history: 0229+131 (quasar 4C 13.14). We obtained a coordinate time series using the analysis strategy of Sect. 3.1, except that $\gamma $ is now fixed to 1, and coordinates of 0229+131 are estimated per session. The closest approach to the Sun is $\sim$1.5$^{\circ }$. At that time, the expected deviation, following Eq. (1), is $\sim$0.3 $^{\prime\prime}$. When parameter $\gamma $ is fixed to unity, this deflection is already corrected and will not show up in the coordinate time series. The obtained right ascension and declination time series are displayed in Fig. 4. The spectrum does not show any significant peak at annual period, indicating that no extra deflection is detectable. Assuming a hypothetical deviation of $\gamma-1$ of $2\times10^{-4}$, the incremental deflection would be as drawn in Fig. 5. Peaking at $\sim$0.03 mas, it is therefore not detectable in the spectrum. It follows that examination of coordinate time series for 0229+131 can only constrain $\gamma $ to be close to unity at approximately the same level of accuracy as already obtained from global estimates.

The evolution in source structure can show up in coordinate time series at lower frequencies as medium or long-term patterns (a few months to years), like the slight curvature showing up in right ascension plotted in Fig. 4. For information about relations between source structure and coordinate time series, the reader can refer to, e.g., Fey et al. (1997), which treats the case of the quasar 4C 39.25.

4 Discussion and conclusion

We have used several methods to look for radio wave deflection in the vicinity of the Sun, starting from a 30-yr routine geodetic VLBI observational data base. We interpret this deflection in terms of gravitational bending, as expressed in Eq. (1). Using several strategies and various data sets covering different time spans, we arrived at the conclusion that $\gamma $ is unity within $2\times10^{-4}$. The estimate of $\gamma $ can even reach values close to unity by $7\times10^{-5}$ when the time span is limited to 1984-2002, i.e., to sessions containing observations of sources at less than 15$^{\circ }$ to the Sun. Although decreasing the formal error due to a larger number of observations, using longer time spans makes the estimates depart from unity by about $1\sigma$.

The main limiting factor is the uncertainty in determinating of (global or session-wise) radio source coordinates. Causes of this uncertainty have been addressed in various works (see, e.g., Ma et al. 1998; Gontier et al. 2001). The VLBI-derived apparent position of a source may change with the global orientation and shape of the antenna array when the structure of the source is extended or not circular. Using Very Long Baseline Array (VLBA) maps at 2 and 8 GHz, Fey & Charlot (1997) provided estimates of the structure delay arising from the extended character of the source. In our example of Sect. 3.3, the structure of 0229+131 is expected to bring an extra delay below 3 ps, let 0.03 mas (see also Ma & Feissel 1997), which partially explains the noise level observed in Fig. 4. It turns out that, in the absence of a direct correction of the delay, based on, e.g., instantaneous maps of the source, the accuracy of $\gamma $ estimates from time series analysis cannot be better than 10-4.

Other potential sources of error are the mismodeling of the propagation delay through the troposphere, as well as deficiencies in the network (e.g., change of geometry and performances from one session to another, dissymmetry between north and south hemispheres). The amplitude of the noise that emerges from them remains difficult to quantify precisely at this time. It is generally admitted that it is as large as the effect of source structure.

Derivation of radio source coordinate time series implies a robust maintenance of the celestial and terrestrial reference frames, so that frame effects do not introduce spurious perturbations of the estimated coordinates. During the derivation process, we checked various analysis strategies and noticed that, when the celestial frame is not sufficiently maintained (e.g., when too few sources are constrained by the NNR), a semi-annual peak could appear at $3\sigma$. In a similar way, fixing the station coordinates to their ITRF values introduces an annual term at the same level. These spurious peaks, which could lead to erroneous physical interpretations in the present context, are good illustrations of the sensitivity of VLBI to reference frames.

Although the mismodeling of the solar corona contribution to light scattering and bending is neglected for geodetic purposes when radio sources are observed at large elongations to the Sun, it becomes crippling for tests of GR since observers do need to observe as close as possible to the Sun. From Sect. 3.1, we tend to conclude that fluctuations in solar coronal plasma limit the accuracy of $\gamma $ estimates at the same level of the sources of error listed above. Thus, various instrumental and modeling errors and analysis strategy defects, that cannot be decorrelated and corrected yet, explain the current limitation of VLBI for estimating $\gamma $.

 \begin{figure} \par\includegraphics[width=7.8cm]{1714fig7.eps}\end{figure} Figure 5:

Theoretical extra deflection from GR model for 0229+131 for $\gamma -1=2\times 10^{-4}$.
Open with DEXTER

Compared to the error reported in Shapiro et al., we do not consider that we have substantially improved the determination of $\gamma $. The slight gain in accuracy can be attributed to the extra years of data (1999-2008), of which the first 4 years (1999-2002) are rich in close approaches, along with the improvement in the quality of the VLBI network and observations during this time. Our work nevertheless constitutes an independent check and provides some qualitative insight into systematics that show up in the analyses of the current geodetic VLBI observational database.

To conclude, we wish to mention that, although current VLBI appears not to be competitive with spacecraft systems for relativistic experiments, the huge number of VLBI measurements, in all directions and at several epochs, constitutes an interesting potential for testing other theories than the PPN formalism, as for example the scenario of Jaeckel & Reynaud (2006) where parameter $\gamma $ is replaced by a function depending on the elongation angle.

Acknowledgements
We are grateful to Drs. Anne-Marie Gontier and Peter Wolf (Observatoire de Paris) for useful discussions about possible tests. We thank Prof. Harald Schuh for his review that helped in improving the paper. This study could not have been carried out without the work of the International VLBI Service for Geodesy and Astrometry (IVS) community that coordinates observations and correlates and stores geodetic VLBI data.

References

All Tables

Table 1:   Characteristics of the solutions and estimates of $\gamma $.

All Figures

  \begin{figure} \par\includegraphics[width=9cm]{1714fig1.eps}\end{figure} Figure 1:

Gravitational delay $\tau _{\rm g}$ as a function of the elongation angle $\phi $ to the Sun for the baseline Westford-Wettzell.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{1714fig2.eps}\end{figure} Figure 2:

Observational history of the sources at less than 30$^{\circ }$ to the Sun. The upper plot gives the Sun spot number (SSN, Clette et al. 2007). The right plot displays the deflection angle as predicted by GR.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8cm]{1714fig3.eps}\includegraphics[width=8cm]{1714fig4.eps}\end{figure} Figure 3:

Estimates of $\gamma $ for various cut-off of the Sun elongation angle. Horizontal, dashed lines figure $\pm \sigma $.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm]{1714fig5.eps}\includegraphics[width=7.8cm]{1714fig6.eps}\end{figure} Figure 4:

(Left) Session-wise coordinates of 0229+131. (Right) Least-squares spectrum.
Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=7.8cm]{1714fig7.eps}\end{figure} Figure 5:

Theoretical extra deflection from GR model for 0229+131 for $\gamma -1=2\times 10^{-4}$.
Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.