| Issue |
A&A
Volume 498, Number 3, May II 2009
|
|
|---|---|---|
| Page(s) | 869 - 875 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200810296 | |
| Published online | 25 March 2009 | |
2D non-LTE radiative modelling of He I spectral lines formed in solar prominences
L. Léger - F. Paletou
Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de Toulouse, CNRS, 14 av. E. Belin, 31400 Toulouse, France
Received 30 May 2008 / Accepted 24 January 2009
Abstract
Context. The interpretation of high-resolution spectropolarimetric observations of solar prominences completed primarily at visible and near-infrared wavelengths, requires radiative modelling that takes into account both multi-dimensional geometry and complex atomic models.
Aims. We enhance the interpretation of observations of He I multiplets, by considering 2D non-LTE unpolarized radiation transfer, and taking into account of the atomic fine-structure of helium.
Methods. We apply our 2D non-LTE radiative transfer code, which is based on the multi-grid Gauss-Seidel/SOR iterative schemes.
Results. It allows us to compute realistic emergent intensity profiles for the He I
![]() Å and D3 multiplets, which can be directly compared to the simultaneous and high-resolution observations completed at THéMIS. A preliminary 2D multi-thread modelling is also discussed.
Å and D3 multiplets, which can be directly compared to the simultaneous and high-resolution observations completed at THéMIS. A preliminary 2D multi-thread modelling is also discussed.
Key words: Sun: prominences - line: profiles - radiative transfer
1 Introduction
Solar prominences (filaments) consist of dense and cool chromospheric plasma suspended in the hot and low density corona (Tandberg-Hanssen 1995). Apart from being a natural laboratory for plasma physics, the study of these structures is of interest to space weather studies. Among other closed magnetic regions such as active regions, eruptive prominences are often associated with coronal mass ejections, or CMEs, which are enormous plasma ``bubbles'' ejected from the solar corona that can strongly affect the Earth environment by their interactions with the terrestrial magnetosphere (see e.g., Gopalswamy et al. 2006, for a review of the various precursors of CMEs).
Despite the systematic observations that have been completed since the nineteenth century and decades of study, prominence formation mechanisms remain poorly understood. For example, no theory can explain their remarkable stability in a hot and less density medium. However, since the plasma ![]() is low inside prominences, the magnetic field is likely to play a major role in the physical scenarios that explain prominence formation, stability, and the triggering of instabilities that generate CMEs.
is low inside prominences, the magnetic field is likely to play a major role in the physical scenarios that explain prominence formation, stability, and the triggering of instabilities that generate CMEs.
He I multiplets such as
![]() Å in the near-infrared, and the Fraunhofer ``yellow line'' D3 at
Å in the near-infrared, and the Fraunhofer ``yellow line'' D3 at
![]() Å are the best tools, so far, to studying prominence magnetic fields. Only a few spectral lines are intense enough for ground-based observations of solar prominences at optical wavelengths i.e., the wavelengths at which spectropolarimetry is usually completed. These helium multiplets provide, even if they are fainter than H
Å are the best tools, so far, to studying prominence magnetic fields. Only a few spectral lines are intense enough for ground-based observations of solar prominences at optical wavelengths i.e., the wavelengths at which spectropolarimetry is usually completed. These helium multiplets provide, even if they are fainter than H![]() for instance, the most valuable data in determining the magnetic field pervading the prominence plasma, even though the helium spectrum, as observed at high spectral resolution, reveals atomic fine-structure. First spectropolarimetric observations of prominences and associated results about the magnetic field properties were reviewed by Paletou & Aulanier (2003) and by López Ariste &
Aulanier (2007).
for instance, the most valuable data in determining the magnetic field pervading the prominence plasma, even though the helium spectrum, as observed at high spectral resolution, reveals atomic fine-structure. First spectropolarimetric observations of prominences and associated results about the magnetic field properties were reviewed by Paletou & Aulanier (2003) and by López Ariste &
Aulanier (2007).
Over the last few years, we have witnessed new advances in observational spectropolarimetry (e.g., the observations of the He I D3 multiplet completed at THéMIS by Paletou et al. 2001), followed by improvements in our ability to determine the magnetic field vector from spectropolarimetric observations of solar prominences in the D3 multiplet implemented by López Ariste & Casini (2002) and Casini et al. (2003). These authors confirmed that expected from Landi Degl'Innocenti (1982) paper about the He I D3 multiplet: by taking account of all Stokes parameters not only linear polarization signals, we can improve the reliability of the magnetic field inferred from observations of the D3 multiplet. Furthermore, the ratio of the intensity of two peaks corresponding to the helium atomic fine-structure of the He I
![]() Å and the D3 multiplets (e.g., Fig. 11 of López Ariste & Casini 2002) often contradicts the commonly
adopted assumption of optically thin multiplets (Bommier 1977).
Å and the D3 multiplets (e.g., Fig. 11 of López Ariste & Casini 2002) often contradicts the commonly
adopted assumption of optically thin multiplets (Bommier 1977).
Another significant advance occured when Trujillo Bueno et al. (2002) clarified the physics controlling the polarization of the He I 10 830 Å triplet (see also Trujillo Bueno & Asensio Ramos 2007), which was followed by applications to spectropolarimetric observations of chromospheric spicules (Trujillo Bueno et al. 2005) and of a polar-crown prominence (Merenda et al. 2006).
The aforementioned investigations of the polarization produced by the joint action of the Hanle and Zeeman effects in the D3 and 10 830 Å multiplets of neutral helium were completed by taking account of their fine-structure and the full impact of level crossings and repulsions. With the computer program HAZEL (from HAnle and ZEeman Light) developed by Asensio Ramos et al. (2008), a standard tool is now available for completing forward-modelling and/or Stokes-inversion investigations of the polarization in these two multiplets. With HAZEL, the effects of radiative transfer can only consider a constant-property slab model, whose optical thickness is chosen to fit the observed intensity profiles. As shown by Centeno et al. (2008), in this basic radiative transfer model the slab's optical thickness accounts implicitly for the true mechanism thought to be responsible for the overall population of the levels of the He I D3 and 10 830 Å multiplets, namely the ionization-recombination mechanism discussed by Avrett et al. (1994) (see also Andretta & Jones 1997; Mauas et al. 2005).
On the other hand, a number of radiative transfer investigations do not account for the polarization of the aforementioned helium multiplets, but aim to provide useful information about the sensitivity of the emergent intensity profiles to various physical parameters. Of particular interest are the recent one-dimensional (1D) static slab models of Labrosse & Gouttebroze (2001, 2004), which produce unrealistic Gaussian profiles because they neglect the fine-structure of the helium multiplets.
Our present paper aims to provide a further step by considering a 2D slab model and the fine-structure of helium. To this end, we applied our own 2D radiative transfer code (Paletou & Léger 2007; Léger et al. 2007), which is based on the multigrid Gauss-Seidel/SOR iterative schemes proposed by Trujillo Bueno & Fabiani Bendicho (1995) and Fabiani Bendicho et al. (1997) for radiative transfer applications.
In Sect. 2 we describe our prominence and atomic models, as well as our numerical strategy. Then, in Sect. 3 we compare and validate our results against previous works of Labrosse & Gouttebroze (2001, 2004). We also show how geometrical effects can influence line profiles. In Sect. 4 we present 2D emergent intensity profiles for the He I
![]() Å and D3 multiplets which can be compared to high-resolution spectropolarimetric observations made at
THéMIS. Finally, we discuss some preliminary results of 2D multi-thread radiative models.
Å and D3 multiplets which can be compared to high-resolution spectropolarimetric observations made at
THéMIS. Finally, we discuss some preliminary results of 2D multi-thread radiative models.
2 Two-dimensional non-LTE radiative modelling
2.1 Geometry and external illumination
We adopted the prominence geometrical model of Vial (1982). As illustrated in Fig. 1, it consists of an isolated 2D slab located above the photosphere. The freestanding slab is supposed to be homogeneous, static, isothermal, and isobaric. It is characterized by two geometrical dimensions of horizontal thickness Dy and vertical extend Dz (the third dimension is infinite in 2D), and its altitude above the photosphere H0. The prominence material is then assumed to consist of neutral and ionized hydrogen, and helium.
The slab is illuminated from below, symmetrically on its sides and bottom, by a photospheric and chromospheric incident radiation field. The latter is diluted according to the chosen altitude above the solar surface, as explained by Paletou (1996). For the helium case, we also consider a constant coronal illumination on the sides and top surfaces. As shown by Avrett et al. (1994), Andretta & Jones (1997), and Mauas et al. (2005), coronal illumination plays an important role in the formation of the He I multiplets, by means of the so-called ``photoionization-recombination'' (PR) mechanism. To take these external illumination conditions accurately into account, we chose depth points logarithmically spaced away from the boundary surfaces towards the slab centre, and symmetrically distributed.
2.2 Numerical strategy
The numerical strategy used is similar to the one described, in 1D, by Labrosse & Gouttebroze (2001, hereafter LG01):
- We solve the statistical equilibrium equations (SEE) including ionization balance, and the non-LTE radiative transfer equations self-consistently, for the multilevel hydrogen atom,
using the previously mentioned 2D radiative transfer code (Paletou & Léger 2007; Léger et al. 2007). We thus obtain bound-level populations and electron densities (see
also Paletou 1995; Heinzel 1995, for the treatment of the ionization equilibrium), which defines the physical conditions to be used as input to the computation of the helium
atom. The ratio of the helium to hydrogen total population densities is
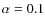 .
We consider further that the helium atom is not an electron donor in the prominence, so that
the electron density given by the hydrogen computation remains constant for the helium computation. Finally, the Lyman continuum opacity and its emissivity are used to model the helium
ultra-violet (UV) lines pumped by the hydrogen continuum.
.
We consider further that the helium atom is not an electron donor in the prominence, so that
the electron density given by the hydrogen computation remains constant for the helium computation. Finally, the Lyman continuum opacity and its emissivity are used to model the helium
ultra-violet (UV) lines pumped by the hydrogen continuum.
- We then solve self-consistently the SEE and the radiative transfer equations for the multilevel helium atom, using the same basic iterative scheme. To take into account the atomic fine structure, we consider the overlapping of all fine structure transitions into a single multi-component radiative transition. For example, the D3 multiplet is a combination of 5 fine structure transitions (see e.g., Fig. 3 in House & Smartt 1982). We thus use, for the helium case, the Rybicki & Hummer (1992) full-preconditioning strategy to solve the SEE including overlapping transitions.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0296fig1.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg18.png) |
Figure 1: 2D geometrical prominence model: the isolated, isothermal and isobaric slab is standing horizontally above the photosphere. For hydrogen and helium atoms, we consider a chromospheric and photospheric incident radiation coming from below, symmetrically on its sides and bottom. For the helium case, we consider in addition a constant coronal illumination coming from above onto the slab. |
| Open with DEXTER | |
In our radiative transfer codes for the hydrogen and helium atoms, we assumed complete redistribution in frequency (CRD).
2.3 Atomic models
We adopted the 5-level plus a continuum hydrogen atom model of Paletou (1995), whose data is consistent with earlier models of Gouttebroze et al. (1993).
For neutral helium, we considered two different cases: 19 bound-levels, up to n=4, plus a continuum, with no atomic fine structure (hereafter our H EN4 model), or 17 bound-levels, up to n=3, plus a continuum, with the atomic fine structure of 23P, 33P, and 33D levels (hereafter, our H EN3 SF model).
Energy levels and statistical weights were taken from the NIST database (Ralchenko et al. 2008). All other atomic data are consistent with those of LG01: effective collision strengths, collisional ionization coefficients, and spontaneous emission coefficients are taken from Benjamin et al. (1999), collision strengths not defined there are from Benson & Kulander (1972), and photoionization cross sections are from TOPbase (Fernley et al. 1987).
Our radiative transfer code can explicitly consider collisional rates among them and to/from all fine structure sublevels. For our H EN3 SF model, we set to 0 the rates between sublevels of the same level. Otherwise, we used, for each sub-level, the rates given by Benjamin et al. (1999), and Benson & Kulander (1972) even though they were summed over the fine-structure. We are aware of this inconsistency, which may affect only slighly the results presented hereafter.
Chromospheric illumination of all radiative transitions were taken from Heasley et al. (1974), with some additional details that can be found in Labrosse et al. (2007). Coronal illumination for UV lines and continua were taken from Tobiska (1991) and Walhstrøm & Carlsson (1994).
3 Preliminary results
As a first step, results obtained with our 2D radiative transfer code for the hydrogen atom are in very good agreement with those of Heasley & Milkey (1983), Gouttebroze et al. (1993), and Paletou (1995)![]() .
.
As a second step, we compared the results obtained with our upgraded 2D radiative transfer code for the helium atom with those of LG01, since these last authors compared their results
comprehensively with the pionneering works of Heasley et al. (1974) and Heasley & Milkey (1978). To complete this comparison, we used our H EN4 model, without atomic fine-structure. Their radiative code is also 1D plane parallel and therefore account for neither coronal illumination on the top surface, nor dilution effects that vary with altitude, unlike 2D models. However, their helium atomic model is more detailed than ours, with 29 bound-levels up to n = 5 for He I, 4 bound-levels for He II, and He III. Unlike ourselves, they also take account of PRD for the resonance lines H I Ly![]() and Ly
and Ly![]() ,
He I
,
He I
![]() Å, and He II
Å, and He II
![]() Å.
Å.
We modelled a 2D prominence with
Dz = 100 000 km and
Dy = 1000 km. Its temperature, T, could be any of values: 6000, 10 000, 14 000, 17 000, and 20 000 K, and its gas pressure ![]() could have one of 2 values: 0.02 and
could have one of 2 values: 0.02 and
![]() .
The microturbulent velocity was fixed at
.
The microturbulent velocity was fixed at
![]() .
The bottom of the slab was set at
H0=10 000 km above the solar surface. We chose a 2D spatial grid with 123
.
The bottom of the slab was set at
H0=10 000 km above the solar surface. We chose a 2D spatial grid with 123 ![]() 123 logarithmically spaced points. We also used Doppler profiles monotonically sampled with a 0.1 step
in Doppler width units.
123 logarithmically spaced points. We also used Doppler profiles monotonically sampled with a 0.1 step
in Doppler width units.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0296fig2.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg24.png) |
Figure 2:
Mean population and electron densities as a function of temperature for two pressures,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0296fig3new.eps}
\par\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg26.png) |
Figure 3:
Emergent intensities for lines He I
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0296fig4new.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg27.png) |
Figure 4: Same as Fig. 3 for a vertical geometrical extension Dz = 10 000 km. |
| Open with DEXTER | |
In Fig. 2, mean population density variations are displayed against temperature. Mean densities are defined to be:
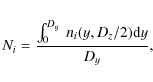
where ni(y,Dz/2) is level i population at position y at the mid-height of the slab (z=Dz/2). We focused on the populations of 5 energy levels of He I:
In the low pressure regime,
![]() ,
we recover the same general behaviour found by LG01: an increase in temperature reduces the mean neutral helium population and
increases the ionized helium mean population, until the latter becomes more numerous than the former. This transition temperature is around 8000 K for our model, whereas it is 11 000 K in LG01. This is explained by PRD effects, since LG01 models in CRD yield the same result as ours (Labrosse, private communication).
,
we recover the same general behaviour found by LG01: an increase in temperature reduces the mean neutral helium population and
increases the ionized helium mean population, until the latter becomes more numerous than the former. This transition temperature is around 8000 K for our model, whereas it is 11 000 K in LG01. This is explained by PRD effects, since LG01 models in CRD yield the same result as ours (Labrosse, private communication).
For higher pressures,
![]() ,
it is shown in Fig. 2 that all mean population densities increase with temperature, apart from the ground state of He I. As
emphasized by LG01, the helium ionization is less important than in the low pressure case, because of the optical thickness of the helium continuum, which prevents incident radiation from reaching the core of the slab. We also recover this effect using our 2D code, when the vertical extension of the slab is sufficiently long, resembling a 1D vertical slab model.
,
it is shown in Fig. 2 that all mean population densities increase with temperature, apart from the ground state of He I. As
emphasized by LG01, the helium ionization is less important than in the low pressure case, because of the optical thickness of the helium continuum, which prevents incident radiation from reaching the core of the slab. We also recover this effect using our 2D code, when the vertical extension of the slab is sufficiently long, resembling a 1D vertical slab model.
We could also check a posteriori, comparing n(He II) and ![]() ,
that the assumption that He is not an electron donor remains valid for most of the range of parameters that we used. As
shown in Fig. 2, it becomes however questionable for both high pressure and high temperature cases.
,
that the assumption that He is not an electron donor remains valid for most of the range of parameters that we used. As
shown in Fig. 2, it becomes however questionable for both high pressure and high temperature cases.
In Fig. 3, emergent intensities for the lines He I
![]() Å,
Å,
![]() Å,
Å,
![]() Å and
Å and
![]() Å are displayed for a vertical extension
Dz=100 000 km, a pressure
Å are displayed for a vertical extension
Dz=100 000 km, a pressure
![]() and for five different temperatures. Intensities are computed at the mid-height of the slab, at z=Dz/2, and for a perpendicular line-of-sight (LOS).
and for five different temperatures. Intensities are computed at the mid-height of the slab, at z=Dz/2, and for a perpendicular line-of-sight (LOS).
The general behaviour of these intensities with temperature is in excellent agreement with results presented by LG01 (see e.g., their Fig. 8). Our values for the intensity of the resonance line He I
![]() Å are smaller than those of LG01, whereas they are larger for the optically thin
Å are smaller than those of LG01, whereas they are larger for the optically thin
![]() Å and
Å and
![]() Å lines. This could be explained by PRD effects that play an important role in determining the shape of the resonance line He I
Å lines. This could be explained by PRD effects that play an important role in determining the shape of the resonance line He I
![]() Å as well as the He I levels 1 and 4 populations. These PRD effects consequently have an impact on the line He I
Å as well as the He I levels 1 and 4 populations. These PRD effects consequently have an impact on the line He I
![]() Å, since its lower level is the level 4, and on ionization by means of the neutral helium continuum
Å, since its lower level is the level 4, and on ionization by means of the neutral helium continuum
![]() Å. The He II ground state mean population density is lower than in LG01. Since the triplet levels are populated by the PR mechanism (see Avrett et al. 1994; Andretta & Jones 1997, and references therein) from the ground state of He II, our D3 multiplet emergent intensity is higher than those of LG01.
Å. The He II ground state mean population density is lower than in LG01. Since the triplet levels are populated by the PR mechanism (see Avrett et al. 1994; Andretta & Jones 1997, and references therein) from the ground state of He II, our D3 multiplet emergent intensity is higher than those of LG01.
In Fig. 4, the same emergent intensities are displayed for a smaller vertical extension of
Dz = 10 000 km (note also that we used, in both cases, the same fixed dilution factor for the
incident radiation, in order to highlight the effects due to different vertical slab extensions). Emergent intensity values are higher, with relative differences ranging between 15% and 40%, than those displayed in Fig. 3. This indicates that significant 2D geometrical effects occur when one reduces the geometrical extension of the slab, and how they impact the magnitude of emergent intensities. These effects were first discovered for H![]() by Paletou (1997).
by Paletou (1997).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0296fig5.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg38.png) |
Figure 5:
Normalized emergent intensities for the He I
|
| Open with DEXTER | |
4 A realistic spectral synthesis of He I multiplets
We now focus on the He I D3 and
![]() Å multiplets, since our primary aim is to model emergent line profiles consistent with high-resolution spectropolarimetric observations
completed at the solar telescope THéMIS (see e.g., Paletou et al. 2001). With this instrument, the two ``red'' and ``blue'' peaks are, indeed, clearly resolved (see also e.g., Merenda
et al. 2006; Trujillo Bueno et al. 2002, for data taken at the German VTT with the TIP polarimeter, in the near-infrared).
Å multiplets, since our primary aim is to model emergent line profiles consistent with high-resolution spectropolarimetric observations
completed at the solar telescope THéMIS (see e.g., Paletou et al. 2001). With this instrument, the two ``red'' and ``blue'' peaks are, indeed, clearly resolved (see also e.g., Merenda
et al. 2006; Trujillo Bueno et al. 2002, for data taken at the German VTT with the TIP polarimeter, in the near-infrared).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0296fig6.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg39.png) |
Figure 6: Same as Fig. 5 for the He I D3 multiplet whose central (vacuum) wavelength is 5877.4 Å. |
| Open with DEXTER | |
Hereafter, in our 2D radiative transfer code we use the H EN3 SF atomic model, which takes into account the atomic fine structure for the
![]() ,
,
![]() ,
and
,
and
![]() levels of He I.
levels of He I.
4.1 Single slab models
We modeled a 2D isobaric, isothermic and static prominence with a vertical extension
Dz=30 000 km and a horizontal extension
Dy=5000 km. Its temperature is T=8000 K, and its gas pressure is
![]() ,
which are typical values for modelling quiescent prominences (see e.g., Gouttebroze et al. 1993). The microturbulent velocity is
,
which are typical values for modelling quiescent prominences (see e.g., Gouttebroze et al. 1993). The microturbulent velocity is
![]() .
The bottom of the slab is assumed to be
H0=10 000 km above the solar surface. We chose a 2D spatial grid with 243
.
The bottom of the slab is assumed to be
H0=10 000 km above the solar surface. We chose a 2D spatial grid with 243 ![]() 243 logarithmically spaced points.
243 logarithmically spaced points.
In Figs. 5 and 6, emergent intensities for He I
![]() Å and D3 multiplets are displayed. They were computed at the slab mid-height, z=Dz/2, for
a LOS perpendicular to the slab, and the specific intensity was normalized to the maximum value obtained with model H EN4. The maximum intensity values are
Å and D3 multiplets are displayed. They were computed at the slab mid-height, z=Dz/2, for
a LOS perpendicular to the slab, and the specific intensity was normalized to the maximum value obtained with model H EN4. The maximum intensity values are
![]() Å-1 for the
Å-1 for the
![]() Å multiplet and
Å multiplet and
![]() Å-1 for the D3 multiplet. Considering the atomic fine-structure, we obtain 2D emergent line profiles that are directly comparable to
high-resolution spectroscopic observations, characterized by two well-resolved subcomponents.
Å-1 for the D3 multiplet. Considering the atomic fine-structure, we obtain 2D emergent line profiles that are directly comparable to
high-resolution spectroscopic observations, characterized by two well-resolved subcomponents.
We define ![]() to be the ratio of the intensity of the largest subcomponent peak and the intensity of the smaller peak, that is,
to be the ratio of the intensity of the largest subcomponent peak and the intensity of the smaller peak, that is,
![]() for the D3 multiplet and
for the D3 multiplet and
![]() for the
for the
![]() Å multiplet. We recall that, when the
He I D3 multiplet becomes optically thick, the
Å multiplet. We recall that, when the
He I D3 multiplet becomes optically thick, the ![]() ratio is lower than 8 (House & Smartt 1982; Landi Degl'Innocenti 1982). Furthermore, the statistical analysis of this ratio infers a mean value of 6 (López Ariste & Casini 2002),
which is inconsistent with the commonly used hypothesis that the D3 multiplet is optically thin.
ratio is lower than 8 (House & Smartt 1982; Landi Degl'Innocenti 1982). Furthermore, the statistical analysis of this ratio infers a mean value of 6 (López Ariste & Casini 2002),
which is inconsistent with the commonly used hypothesis that the D3 multiplet is optically thin.
We can evaluate the optical thickness of the two multiplets obtained with our 2D model. At the slab mid-height, z=Dz/2, and for the frequency corresponding to the maximum intensity value, we calculate
The two multiplets are thus optically thin, and we also find that
Having performed several tests with temperatures varying from 6000 to 20 000 K and for gas pressures ranging from 0.02 to
![]() ,
we found that the two multiplets are optically thicker for both high pressure and high temperature atmospheres. However, even in these regimes, the optical thicknesses of the D3 multiplet never exceed
,
we found that the two multiplets are optically thicker for both high pressure and high temperature atmospheres. However, even in these regimes, the optical thicknesses of the D3 multiplet never exceed
![]() .
These results are also in accordance with 1D models of Labrosse & Gouttebroze (2004). For instance, these authors found no model for which the D3 multiplet is optically thick, and
.
These results are also in accordance with 1D models of Labrosse & Gouttebroze (2004). For instance, these authors found no model for which the D3 multiplet is optically thick, and
![]() for models where T>20 000 K and
for models where T>20 000 K and
![]() ,
i.e., conditions that are not representative of those expected in quiescent prominences.
,
i.e., conditions that are not representative of those expected in quiescent prominences.
Which type of model could reproduce the observed ratio between the subcomponents of the 557.6 and 1083. nm multiplets of He I?
| |
Figure 7: A sketch of the 2D multi-thread prominence model that we adopted. Individual threads are superimposed along the line-of-sight, and there is no radiative interaction between them. Emergent intensities are computed as formal solutions of the radiative transfer equation along a line-of-sight perpendicular to the thread vertical extension, to take into account the contribution of each individual thread. |
| Open with DEXTER | |
4.2 2D multi-thread models
We thus decided to model prominences differently, using the fact that they consist of small-scale threads. This is supported both by observations (e.g., Berger et al. 2008; Lin et al. 2005) and MHD simulations (e.g., Low & Petrie 2005). The effect of the increased penetration of the incident radiation, using multiple layer modelling, was also shown in 1D by Gouttebroze et al. (2002). This 2D non-LTE spatial fine-structure radiative modelling of solar prominences was used by Gunár et al. (2007), in interpreting UV observations of the Lyman series of hydrogen completed with the SUMER spectrograph onboard SoHO.
Hereafter, all the 2D threads (see Fig. 7) are supposed to be identical and located at the same altitude, with similar horizontal and vertical extensions
Dy=Dz=1200 km corresponding to a
![]() arcsec angular resolution consistent with that achieved by spectropolarimetry of prominences using ground-based observatories. This choice can obviously be debated, and we could have considered (much) smaller threads, at smaller scale than the spatial resolution (see e.g., Vial 2006; Heinzel 2007). However, we leave more detailed investigations of this to future studies.
arcsec angular resolution consistent with that achieved by spectropolarimetry of prominences using ground-based observatories. This choice can obviously be debated, and we could have considered (much) smaller threads, at smaller scale than the spatial resolution (see e.g., Vial 2006; Heinzel 2007). However, we leave more detailed investigations of this to future studies.
We also considered that there is no radiative interaction between individual threads. Thus, as a first step, we applied our 2D radiative transfer code to one individual thread. We then computed emergent intensities as the formal solution of the radiative transfer equation along a LOS perpendicular to each thread's vertical extension, in order to account for the contribution of a bunch of threads. Therefore, the total optical thickness along the LOS is simply the sum of the optical thicknesses of each individual thread.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0296fig8.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg56.png) |
Figure 8:
The |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0296fig9.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg57.png) |
Figure 9:
Same as Fig. 8 for the |
| Open with DEXTER | |
For each (identical) thread, we adopted a gas pressure
![]() and a temperature T=8000 K corresponding to a commonly used temperature for quiescent prominences (see e.g., Engvold et al. 1990; Tandberg-Hanssen 1995).
and a temperature T=8000 K corresponding to a commonly used temperature for quiescent prominences (see e.g., Engvold et al. 1990; Tandberg-Hanssen 1995).
In Figs. 8 and 9, we plot the ![]() ratio versus the number of threads along the LOS, for the He I
ratio versus the number of threads along the LOS, for the He I
![]() Å and D3 multiplets. For the
calculation of this ratio, we calculated the emergent specific intensity integrated over Dz, that is:
Å and D3 multiplets. For the
calculation of this ratio, we calculated the emergent specific intensity integrated over Dz, that is:
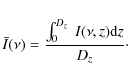
The total optical thickness, integrated in a similar way, is also displayed on the same plots.
We can thus determine the number of threads required, with these models, to obtain a ![]() ratio around 6 for the He I D3 multiplet. In this case, a good value is around 30 threads, which corresponds, however, to a large total geometrical width of 36 000 km for the prominence. The corresponding optical thickness is
ratio around 6 for the He I D3 multiplet. In this case, a good value is around 30 threads, which corresponds, however, to a large total geometrical width of 36 000 km for the prominence. The corresponding optical thickness is
![]() .
For a temperature
T = 17 000 K, corresponding to a prominence-to-corona transition region (PCTR, see
e.g., Fontenla et al. 1996; Anzer & Heinzel 1999, and references therein), the number of threads decreases to 15, and
.
For a temperature
T = 17 000 K, corresponding to a prominence-to-corona transition region (PCTR, see
e.g., Fontenla et al. 1996; Anzer & Heinzel 1999, and references therein), the number of threads decreases to 15, and
![]() .
.
Even though our analysis is still preliminary, yet we favour multi-thread models in explaining a number of properties of observed He I spectral lines.
However, we are also aware that, even in a non-magnetic field regime, Stokes I is affected by atomic polarization (Casini, private communication). Therefore, a more detailed comparison with spectropolarimetric data would require a more complex treatment of the statistical equilibrium.
5 Conclusion
We have performed several tests to compare our new 2D radiative model with previous works. Results for the hydrogen atom have been compared with those of Heasley & Milkey (1983), Gouttebroze et al. (1993), and Paletou (1995). Results for the helium atom have been compared mainly with Labrosse & Gouttebroze (2001, 2004). Excellent agreement is achieved using our 2D code in the limit of a 1D geometry, with similar atomic models and incident radiation.
We have shown that, by taking account of the atomic fine-structure for the
![]() ,
,
![]() ,
and
,
and
![]() levels of He I in our 2D radiative transfer code, we can compute emergent line profiles, which can be compared directly with those derived from high-spectral
resolution observations. However, using a classical model of isothermal, isobaric, homogeneous, and static slabs leads to ratios between the subcomponents of He I
levels of He I in our 2D radiative transfer code, we can compute emergent line profiles, which can be compared directly with those derived from high-spectral
resolution observations. However, using a classical model of isothermal, isobaric, homogeneous, and static slabs leads to ratios between the subcomponents of He I
![]() Å and
D3 multiplets that disagree observed values, except for high temperature and high pressure conditions, which are atypical of quiescent prominences (Engvold et al. 1990).
Å and
D3 multiplets that disagree observed values, except for high temperature and high pressure conditions, which are atypical of quiescent prominences (Engvold et al. 1990).
This inspired us to undertake a preliminary investigation of 2D multi-thread modelling. This provided good hints in reproducing observed characteristics of the D3 and
![]() Å multiplets of He I, such as the ratio between the intensity of
their two subcomponents.
Å multiplets of He I, such as the ratio between the intensity of
their two subcomponents.
Our 2D radiative model will be more intensively used, by modelling smaller threads, eventually beyond spatial resolution (see Heinzel 2007, for a review), and the radiative interaction between these threads (e.g., Heinzel 1989). We shall also include a PCTR for each individual thread in our model, since its influence on hydrogen lines have already been evaluated.
We finally anticipate that our results will be invaluable in analysing data from a variety of spaceborne (e.g., SoHO, Hinode) and ground-based telescopes such as THéMIS.
Acknowledgements
We are grateful to Drs. Juan Fontenla (LASP, U. of Colorado), Nicolas Labrosse (U. Glasgow) and Petr Heinzel (Ondrejov) for fruitful discussions, suggestions and comments they provided to us during the course of this study. THéMIS is operated on the Island of Tenerife by CNRS-CNR in the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias.
References
- Andretta, V., & Jones, H. P. 1997, ApJ, 489, 375 [NASA ADS] [CrossRef] (In the text)
- Anzer, U., & Heinzel, P. 1999, A&A, 349, 974 [NASA ADS] (In the text)
- Avrett, E. H., Fontenla, J. M., & Loeser, R. 1994, in Infrared Solar Physics, ed. D. M. Rabin, J. T. Jefferies, & C. Lindsey (Dordrecht: Kluwer), IAU Symp., 154, 35 (In the text)
- Asensio Ramos, A., Trujillo Bueno, J., & Landi Degl'Innocenti, E. 2008, ApJ, 683, 542 [NASA ADS] [CrossRef] (In the text)
- Benjamin, R. A., Skillman, E. D., & Smits, D. P. 1999, ApJ, 514, 307 [NASA ADS] [CrossRef] (In the text)
- Benson, R. S., & Kulander, J. L. 1972, Sol. Phys., 27, 305 [NASA ADS] [CrossRef] (In the text)
- Berger, T. E., Shine, R. A., Slater, G. L., et al. 2008, ApJ, 676, L89 [NASA ADS] [CrossRef] (In the text)
- Bommier, V. 1977, Thèse de Doctorat de 3ème cycle, Univ. de Paris VI (In the text)
- Casini, R., López Ariste, A., Tomczyk, S., & Lites, B. W. 2003, ApJ, 598, 67 [NASA ADS] [CrossRef] (In the text)
- Centeno, R., Trujillo Bueno, J., Uitenbroek, H., & Collados, M. 2008, ApJ, 677, 742 [NASA ADS] [CrossRef] (In the text)
- Engvold, O., Hirayama, T., Leroy, J.-L., Priest, E. R., & Tandberg-Hanssen, E. 1990, in Dynamics of Quiescent Prominences, ed. V. Ruzdjak, & E. Tandberg-Hanssen (New-York: Springer-Verlag), Lecture Notes in Physics, 363, 294 (In the text)
- Fabiani Bendicho, P., Trujillo Bueno, J., & Auer, L. H. 1997, A&A, 324, 161 [NASA ADS] (In the text)
- Fernley, J. A., Seaton, M. J., & Taylor, K. T. 1987, J. Phys. B, 20, 6457 [NASA ADS] [CrossRef] (In the text)
- Fontenla, J. M., Rovira, M., Vial, J.-C., & Gouttebroze, P. 1996, ApJ, 466, 511 [CrossRef] (In the text)
- Gopalswamy, N., Mikic, Z., Maia, D., et al. 2006, Space Sci. Rev., 123, 303 [NASA ADS] [CrossRef] (In the text)
- Gouttebroze, P., Heinzel, P., & Vial, J.-C. 1993, A&AS, 99, 513 [NASA ADS] (In the text)
- Gouttebroze, P., Labrosse, N., Heinzel, P., & Vial, J.-C. 2002, ESA-SP, 505, 421 [NASA ADS] (In the text)
- Gunár, S., Heinzel, P., Schmieder, B., Schwartz, P., & Anzer, U. 2007, A&A, 472, 929 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Heasley, J. N., & Milkey, R. W. 1978, ApJ, 221, 677 [NASA ADS] [CrossRef] (In the text)
- Heasley, J. N., & Milkey, R. W. 1983, ApJ, 268, 398 [NASA ADS] [CrossRef] (In the text)
- Heasley, J. N., Mihalas, D., & Poland, A. I. 1974, ApJ, 192, 181 [NASA ADS] [CrossRef] (In the text)
- Heinzel, P. 1989, Hvar Obs. Bull., 13(1), 317 (In the text)
- Heinzel, P. 1995, A&A, 299, 563 [NASA ADS] (In the text)
- Heinzel, P. 2007, in The Physics of Chromospheric Plasmas, ed. P. Heinzel, I. Dorotovic, & R. J. Rutten (San Francisco: ASP), ASP Conf. Ser., 368, 271 (In the text)
- House, L. L., & Smartt, R. N. 1982, Sol. Phys., 80, 53 [NASA ADS] [CrossRef] (In the text)
- Labrosse, N., & Gouttebroze, P. 2001, A&A, 380, 323 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Labrosse, N., & Gouttebroze, P. 2004, ApJ, 617, 614 [NASA ADS] [CrossRef] (In the text)
- Labrosse, N., Gouttebroze, P., & Vial, J.-C. 2007, A&A, 463, 1171 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Landi Degl'Innocenti, E. 1982, Sol. Phys., 79, 291 [NASA ADS] [CrossRef] (In the text)
- Léger, L., Chevallier, L., & Paletou, F. 2007, A&A, 470, 1 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lin, Y., Engvold, O., Rouppe van der Voort, L. H. M., Wiik, J. E., & Berger, T. E. 2005, Sol. Phys., 226, 239 [NASA ADS] [CrossRef] (In the text)
- López Ariste, A., & Aulanier, G. 2007, in The Physics of Chromospheric Plasmas, ed. P. Heinzel, I. Dorotovic, & R. J. Rutten (San Francisco: ASP), ASP Conf. Ser., 368, 291 (In the text)
- López Ariste, A., & Casini, R. 2002, ApJ, 575, 529 [NASA ADS] [CrossRef] (In the text)
- Low, B. C., & Petrie, G. J. D. 2005, ApJ, 626, 551 [NASA ADS] [CrossRef] (In the text)
- Mauas, P. J. D., Andretta, V., Falchi, A., et al. 2005, ApJ, 619, 604 [NASA ADS] [CrossRef] (In the text)
- Merenda, L., Trujillo Bueno, J., Landi Degl'Innocenti, E., & Collados, M. 2006, ApJ, 642, 544 [CrossRef] (In the text)
- Paletou, F. 1995, A&A, 302, 587 [NASA ADS] (In the text)
- Paletou, F. 1996, A&A, 311, 708 [NASA ADS] (In the text)
- Paletou, F. 1997, A&A, 317, 244 [NASA ADS] (In the text)
- Paletou, F., & Aulanier, G. 2003, in Solar Polarization Workshop 3, ed. J. Trujillo Bueno, & J. Sánchez Almeida (San Francisco: ASP), ASP Conf. Ser., 307, 458 (In the text)
- Paletou, F., & Léger, L. 2007, JQSRT, 103, 57 [NASA ADS] (In the text)
- Paletou, F., López Ariste, A., Bommier, V., & Semel, M. 2001, A&A, 375, 39 [NASA ADS] [CrossRef] (In the text)
- Ralchenko, Yu., Kramida, A. E., Reader, J., & NIST ASD Team 2008, NIST Atomic Spectra Database, version 3.1.5, available online: http://physics.nist.gov/asd3, National Institute of Standards and Technology, Gaithersburg, MD, USA (In the text)
- Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 [NASA ADS] (In the text)
- Tandberg-Hanssen, E. 1995, The Nature of Solar Prominences (Dordrecht: Kluwer) (In the text)
- Tobiska, W. K. 1991, J. Atmos. Terr. Phys., 53, 1005 [NASA ADS] [CrossRef] (In the text)
- Trujillo Bueno, J., & Asensio Ramos, A. 2007, ApJ, 655, 642 [NASA ADS] [CrossRef] (In the text)
- Trujillo Bueno, J., & Fabiani Bendicho, P. 1995, ApJ, 455, 646 [NASA ADS] [CrossRef] (In the text)
- Trujillo Bueno, J., Landi Degl'Innocenti, E., Collados, M., Merenda, L., & Manso Sainz, R. 2002, Nature, 415, 403 [NASA ADS] [CrossRef] (In the text)
- Trujillo Bueno, J., Merenda, L., Centeno, R., Collados, M., & Landi Degl'Innocenti, E. 2005, ApJ, 619, 191 [NASA ADS] [CrossRef] (In the text)
- Vial, J.-C. 1982, ApJ, 254, 780 [NASA ADS] [CrossRef] (In the text)
- Vial, J.-C. 2006, ESA SP-617, 163 (In the text)
- Vial, J.-C., Rovira, M., Fontenla, J. M., & Gouttebroze, P. 1989, Hvar Obs. Bull., 13(1), 347
- Walhstrøm, C., & Carlsson, M. 1994, ApJ, 433, 417 [NASA ADS] [CrossRef] (In the text)
Footnotes
- ...1995)
![[*]](/icons/foot_motif.png)
- In this article, partial redistribution in frequency (PRD) was used by default, but we could make direct comparisons with a CRD version of this previous code.
All Figures
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0296fig1.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg18.png) |
Figure 1: 2D geometrical prominence model: the isolated, isothermal and isobaric slab is standing horizontally above the photosphere. For hydrogen and helium atoms, we consider a chromospheric and photospheric incident radiation coming from below, symmetrically on its sides and bottom. For the helium case, we consider in addition a constant coronal illumination coming from above onto the slab. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0296fig2.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg24.png) |
Figure 2:
Mean population and electron densities as a function of temperature for two pressures,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0296fig3new.eps}
\par\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg26.png) |
Figure 3:
Emergent intensities for lines He I
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{0296fig4new.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg27.png) |
Figure 4: Same as Fig. 3 for a vertical geometrical extension Dz = 10 000 km. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0296fig5.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg38.png) |
Figure 5:
Normalized emergent intensities for the He I
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0296fig6.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg39.png) |
Figure 6: Same as Fig. 5 for the He I D3 multiplet whose central (vacuum) wavelength is 5877.4 Å. |
| Open with DEXTER | |
| In the text | |
| |
Figure 7: A sketch of the 2D multi-thread prominence model that we adopted. Individual threads are superimposed along the line-of-sight, and there is no radiative interaction between them. Emergent intensities are computed as formal solutions of the radiative transfer equation along a line-of-sight perpendicular to the thread vertical extension, to take into account the contribution of each individual thread. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0296fig8.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg56.png) |
Figure 8:
The |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{0296fig9.eps}
\end{figure}](/articles/aa/full_html/2009/18/aa10296-08/Timg57.png) |
Figure 9:
Same as Fig. 8 for the |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


