| (10) |
Under stationarity, the thermal structure of an atomic (perfect) gas
with density n and temperature T is given by the first law of
thermodynamics:
The gas considered here is composed of electrons, ions and neutrals of
several atomic species, namely
![]() where the overline stands for a sum over all present
chemical elements. We then define the density of nuclei
where the overline stands for a sum over all present
chemical elements. We then define the density of nuclei
![]() and the electron density
and the electron density
![]() .
Correspondingly, the total velocity
.
Correspondingly, the total velocity ![]() appearing in Eq. (10) must be understood as the
barycentric velocity. As usual in one-fluid approximation, we suppose
- and verify it in Sect. C.1 - all species well
coupled (through collisions), so that they share the same temperature
T. We also assume that no molecule formation occurs, so that mass
conservation requires
appearing in Eq. (10) must be understood as the
barycentric velocity. As usual in one-fluid approximation, we suppose
- and verify it in Sect. C.1 - all species well
coupled (through collisions), so that they share the same temperature
T. We also assume that no molecule formation occurs, so that mass
conservation requires
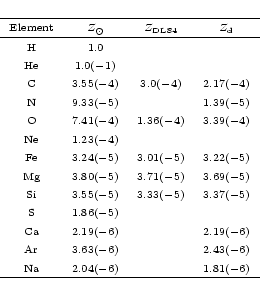
We solve the gas ionization state (Eqs. (12) to (14)) using the Mappings Ic code - Binette et al. (1985); Binette & Robinson (1987); Ferruit et al. (1997). This code considers atomic gas composed by the chemical elements H, He, C, N, O, Ne, Fe, Mg, Si, S, Ca, Ar. We also added Na (whose ionization evolution is not solved by Mappings Ic), assuming it to be completely ionized in Na II. Hydrogen and Helium are treated as five level atoms.
The rate equations solved by Mappings Ic include photoionization, collisional ionization, secondary ionization due to energetic photoelectrons, charge exchange, recombination and dielectronic recombination. This is in contrast with Safier, who assumed a fixed ionization fraction for the heavy elements and solved only for the ionization evolution of H and He, considering two levels for H and only the ground level for He.
The adopted abundances are presented in Table 2. In contrast with Safier, we take into account heavy element depletion onto dust grains (see Sect. 3.2.3 and Appendix B) in the dusty region of the wind.
|
For simplicity, the central source radiation field is described in exactly the same way as in Safier and we refer the reader to the expressions (C1-C10) presented in his Appendix C. This radiation field is diluted with distance but is also absorbed by intervening wind material ejected at smaller radii.
We treat the radiative transfer as a simple absorption of the diluted
central source, namely
We now address the question of optical depth. In our model, the flow
is hollow, starting from a ring located at the inner disk radius
![]() and extending to the outer radius
and extending to the outer radius
![]() .
The jet inner boundary is therefore exposed to the central ionizing
radiation, which produces then a small layer where hydrogen is
completely photoionized. The width
.
The jet inner boundary is therefore exposed to the central ionizing
radiation, which produces then a small layer where hydrogen is
completely photoionized. The width ![]() of this layer can be
computed by equating the number of emitted H ionizing photons,
of this layer can be
computed by equating the number of emitted H ionizing photons,
![]() ,
to the
number of recombinations in this layer,
,
to the
number of recombinations in this layer,
![]() for our geometry. We found that
for our geometry. We found that
![]() ,
and thus assume that all photons capable of ionizing hydrogen are
exhausted within this thin shell. Furthermore, there is presumably
matter in the inner "hollow'' region, so the previous considerations
are upper limits.
,
and thus assume that all photons capable of ionizing hydrogen are
exhausted within this thin shell. Furthermore, there is presumably
matter in the inner "hollow'' region, so the previous considerations
are upper limits.
For the heavy elements, photoionization optical depths are negligible,
due to the much smaller abundances, and are thus ignored. The opacity
![]() is assumed to be dominated by dust absorption (see
Appendix B for details). Dust will influence the
ionization structure at the base of the flow, where ionization is
dominated by heavy elements.
is assumed to be dominated by dust absorption (see
Appendix B for details). Dust will influence the
ionization structure at the base of the flow, where ionization is
dominated by heavy elements.
To summarize, the adopted radiation field is a central source absorbed by dust, with a cutoff at and above the Hydrogen ionization frequency.
Safier showed that if dust exists inside the disk, then the wind drag will lift the dust thereby creating a dusty wind. Our wind shares the same property. We model the dust (Appendix B) as a mix of graphite and astronomical silicate, with a MRN size distribution and use for the dust optical properties the tabulated values of Draine & Lee (1984), Draine & Malhotra (1993), Laor & Draine (1993). For simplicity we assumed the dust to be stationary, in thermodynamic equilibrium with the central radiation field and averaged all dust quantities by the MRN size distribution.
In addition, we take into account depletion of heavy elements into the
dust phase. This effect was not considered by Safier.
In Table 2 we present the dust phase abundances needed to maintain the
MRN distribution (Draine & Lee), and our adopted depleted
abundances, taken from observations of diffuse clouds toward ![]() Ori (Savage & Sembach 1996). These are more realistic, although presenting
less depletion of carbon than required by MRN. Depletion has only a
small effect on the calculated wind thermal structure, but can be
significant when comparing to observed line ratios based on depleted
elements.
Ori (Savage & Sembach 1996). These are more realistic, although presenting
less depletion of carbon than required by MRN. Depletion has only a
small effect on the calculated wind thermal structure, but can be
significant when comparing to observed line ratios based on depleted
elements.
The dissipation of electric currents ![]() provides a local heating
term per unit volume
provides a local heating
term per unit volume
![]() ,
where
,
where ![]() and
and ![]() are the
electric and magnetic fields,
are the
electric and magnetic fields, ![]() the fluid velocity and cthe speed of light. In a multi-component gas, with electrons and
several ion and neutral species, the generalized Ohm's law writes
the fluid velocity and cthe speed of light. In a multi-component gas, with electrons and
several ion and neutral species, the generalized Ohm's law writes
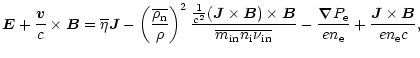 |
(16) |
The first term appearing in the right hand side of the generalized
Ohm's law is the usual Ohm's term, while the second describes the
ambipolar diffusion, the third is the electric field due to the
electron pressure and the last is the Hall term. This last effect
provides no net dissipation in contrary to the other three. It turns
out that the dissipation due to the electronic pressure is quite
negligible and has been therefore omitted (Appendix C).
Thus, the MHD dissipation writes
An important difference with Safier is that we take
into account thermal speeds in ion-neutral momentum exchange rate
coefficients. This increases
![]() ,
and results in significantly
smaller ionization fractions (Sect. 4.8).
,
and results in significantly
smaller ionization fractions (Sect. 4.8).
Both collisional ionization cooling
![]() and
radiative recombination cooling
and
radiative recombination cooling
![]() effects are
taken into account by Mappings Ic. These terms are given by,
effects are
taken into account by Mappings Ic. These terms are given by,
| = | 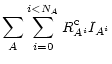 |
(18) | |
| = | 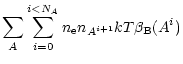 |
(19) |
These ionization/recombination effects, taken into account in part by Safier, are in general smaller than adiabatic and line cooling.
Photoionization by the radiation field, not taken into account by
Safier, provides an extra source of heating
![]() .
This term, which is also computed by Mappings Ic, is given by
.
This term, which is also computed by Mappings Ic, is given by
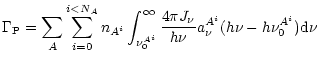 |
(20) |
Collisionally excited lines provide a very efficient way to cool the
gas, thanks to an extensive set of resonance and inter-combination
lines, as well as forbidden lines. This radiative cooling
![]() is computed by Mappings Ic by solving for
each atom the local statistical equilibrium, and will allow us to
compute emission maps and line profiles for comparison with
observations (see Garcia et al. 2001). We include cooling by
hydrogen lines,
is computed by Mappings Ic by solving for
each atom the local statistical equilibrium, and will allow us to
compute emission maps and line profiles for comparison with
observations (see Garcia et al. 2001). We include cooling by
hydrogen lines,
![]() ,
in particular H
,
in particular H![]() ,
which could not be computed by Safier (two-level atom
description).
,
which could not be computed by Safier (two-level atom
description).
Several processes, also computed by Mappings Ic, appeared to be very small and not affecting the jet thermal structure. We just cite them here for completeness: free-free cooling and heating, two-photon continuum and Compton scattering.
We ignored thermal conduction, which could be relevant along flow lines, the magnetic field reducing the gas thermal conductibility in any other direction. Also ignored was gas cooling by dust grains and heating by cosmic rays. We checked a posteriori that these three terms indeed have a negligible contribution (see Appendix C.2).
In our study, flow thermodynamics are decoupled from the dynamics -
cold jet approximation. The previous Eqs. (10) to (14) can then be integrated for a given flow pattern.
The dynamical quantities (density, velocity and magnetic fields) are
given by the cold MHD solutions presented in Sect. 2. For
the steady-state, axisymmetric, self-similar MHD winds under study,
any total derivative writes
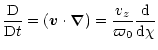 |
(21) |
The integration of the set Eqs. (12) to (14) and (22) along the flow is an initial value problem. Thus, some way to estimate the initial temperature and populations must be devised. All calculations start at the slow-magnetosonic (SM) point, which is roughly at two scale heights above the disk midplane (for the solutions used here).
To estimate the initial temperature, Safier equated
the poloidal flow speed at the SM point to the sound speed. Although
this estimation agrees with cold flow theory, it is inconsistent with
the energy equation which is used further up in the jet. Our approach
was then to compute the initial temperature and ionic populations
assuming that
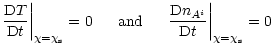 |
(23) |
The initial populations are computed by Mappings Ic assuming ionization equilibrium with the incoming radiation field. However for high accretion rates and for the outer zones of the wind, dust opacity and inclination effects shield completely the ionizing radiation field. The temperature is too low for collisional ionization to be effective. The ionization fraction thus reaches our prescribed minimum - all Na is in the form Na II (Table 2) and all the other elements (computed by Mappings Ic) neutral. However, soon the gas flow gains height and the ionization field is strong enough such that the ionization is self-consistently computed by Mappings Ic.
After obtaining an initial temperature and ionization state for the
gas we proceed by integrating the system of equations. In practice the
ionization evolution is computed by Mappings Ic and separately
we integrate Eq. (22) with a Runge-Kutta type algorithm
(Press et al. 1988). We maintain both the populations and Mappings Ic cooling/heating rates per
![]() fixed during each
temperature integrating spatial step. After we call Mappings Ic
to evolve the populations and rates, at the new temperature, during
the time taken by the fluid to move the spatial step. This step is
such, that the RK integration has a numerical accuracy of 10-6and, that the newly computed temperature varies by less than a factor
of 10-4. Such a small variation in temperature allows us to
assume constant rates and populations while solving the energy
equation. We checked a few integrations by redoing them at half the
step used and found that the error in the ionic fraction is
<10-3in the jet, and
< 10-2 in the recollimation zone; the temperature
precision being roughly a few times better. This ensures an intrinsic
numerical precision comfortably below the accuracy of the atomic data
and the
fixed during each
temperature integrating spatial step. After we call Mappings Ic
to evolve the populations and rates, at the new temperature, during
the time taken by the fluid to move the spatial step. This step is
such, that the RK integration has a numerical accuracy of 10-6and, that the newly computed temperature varies by less than a factor
of 10-4. Such a small variation in temperature allows us to
assume constant rates and populations while solving the energy
equation. We checked a few integrations by redoing them at half the
step used and found that the error in the ionic fraction is
<10-3in the jet, and
< 10-2 in the recollimation zone; the temperature
precision being roughly a few times better. This ensures an intrinsic
numerical precision comfortably below the accuracy of the atomic data
and the
![]() collision cross-sections
which, coupled to abundance incertitudes, are the main limitating
factors. Details on the actual numerical procedure used by Mappings Ic to compute the non-equilibrium gas evolution are given in
Binette et al. (1985).
collision cross-sections
which, coupled to abundance incertitudes, are the main limitating
factors. Details on the actual numerical procedure used by Mappings Ic to compute the non-equilibrium gas evolution are given in
Binette et al. (1985).
Copyright ESO 2001