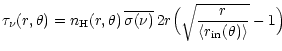Up: Atomic T Tauri disk winds
Appendix B: Dust implementation
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{figb1.epsi} \end{figure}](/articles/aa/full/2001/38/aa1260/Timg353.gif) |
Figure B.1:
Dust sublimation surfaces geometry for the adopted radiation
field. |
As shown by Safier if there is dust in the disk, the
wind is powerful enough to drag it along. Thus disk winds are dusty
winds. Dust is important for the wind thermal structure mainly as an
opacity source affecting the photoionisation heating at the wind
base. To compute the dust opacity we need a description of its size
distribution, its wavelength dependent absorption cross-section and
the inner dust sublimation surface. In the inner flow zones and for
high accretion rates the strong stellar and boundary layer flux will
sublimate the dust, creating a dust free inner cavity (see
Fig. B.1). Results on the evolution of dust in
accretion disks by Schmitt et al. (1997) show that at the disk surface the
initial dust distribution isn't much affected by coagulation and
sedimentation effects. Thus we assume a MRN dust distribution
(Mathis et al. 1977; Draine & Lee 1984):
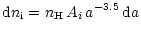 |
|
|
(B.1) |
where
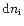 is the number of particles of type i ("astronomical
silicate'' - Sil or graphite - C) with sizes in
is the number of particles of type i ("astronomical
silicate'' - Sil or graphite - C) with sizes in
![$[a,a+{\rm d}a]$](/articles/aa/full/2001/38/aa1260/img356.gif) ,
and
,
and
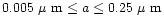 ,
,
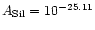 cm2.5 H-1 and
cm2.5 H-1 and
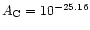 cm2.5 H-1. We then proceed by averaging all relevant grain
quantities function of size and species (Fi(a)) by the size/species
distribution,
cm2.5 H-1. We then proceed by averaging all relevant grain
quantities function of size and species (Fi(a)) by the size/species
distribution,
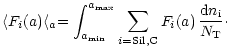 |
|
|
(B.2) |
In order to compute the sublimation radius, some description of the
dust temperature must be made. For simplicity, we assume the dust to
be in thermodynamic equilibrium with the radiation field, the dominant
dust heating mechanism. In our case, the central source radiation
field will dominate throughout the jet, except probably in the
recollimation zone, where the strong gas emission overcomes the
central diluted field. However in this region dust is no longer
relevant for the gas thermodynamics and we will therefore only
consider dust heating by the central source. The dust temperature
 for a grain of size a is obtained by equating the
absorbed to the emitted radiation (e.g., Tielens & Hollenbach 1985),
for a grain of size a is obtained by equating the
absorbed to the emitted radiation (e.g., Tielens & Hollenbach 1985),
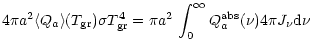 |
|
|
(B.3) |
where a is the grain size
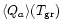 is the
Planck-averaged emissivity (Draine & Lee 1984; Laor & Draine 1993; Draine & Malhotra 1993),
is the
Planck-averaged emissivity (Draine & Lee 1984; Laor & Draine 1993; Draine & Malhotra 1993), 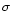 is the Stefan-Boltzmann constant,
is the Stefan-Boltzmann constant,
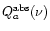 is the dust absorption efficiency
is the dust absorption efficiency![[*]](/icons/foot_motif.gif) and
and
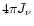 is the central source radiation flux at the grain position
given by Eq. (15). Averaging out the previous equation by
the size/species distribution (Eq. (B.2)) we obtain,
is the central source radiation flux at the grain position
given by Eq. (15). Averaging out the previous equation by
the size/species distribution (Eq. (B.2)) we obtain,
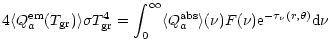 |
|
|
(B.4) |
where we describe the central source flux by 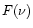 which is
attenuated only by the dust opacity
which is
attenuated only by the dust opacity 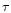 .
For simplicity
.
For simplicity 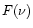 is
taken as exactly the same as in Safier, i.e. a
classical boundary layer (Bertout et al. 1988). The sublimation radius is
obtained from the previous expression by noting that at its position
is
taken as exactly the same as in Safier, i.e. a
classical boundary layer (Bertout et al. 1988). The sublimation radius is
obtained from the previous expression by noting that at its position
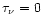 ,
,
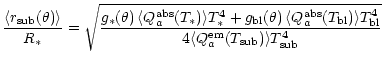 |
|
|
(B.5) |
where
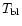 and
and 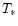 are the boundary layer and star
temperatures,
are the boundary layer and star
temperatures, 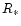 the stellar radius and
the stellar radius and
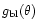 /
/
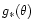 are the
are the 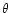 dependent terms of the
radiation field (given in Bertout et al. and Safier).
We assume a dust sublimation temperature
dependent terms of the
radiation field (given in Bertout et al. and Safier).
We assume a dust sublimation temperature
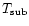 of 1500 K.
of 1500 K.
With the dust sublimation radius in hand we can now proceed to compute
the dust optical depth defined as,
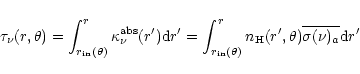 |
(B.6) |
where
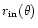 is the radius inside which there is no
dust. This radius is given by the inner flow line
is the radius inside which there is no
dust. This radius is given by the inner flow line
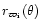 and by the sublimation radius
and by the sublimation radius
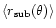 (see Fig. B.1) such that
(see Fig. B.1) such that
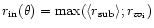 .
The
dust absorption cross-section (
.
The
dust absorption cross-section (
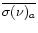 )
is,
)
is,
![$\displaystyle \overline{\sigma(\nu)_a}=\int_{a_{\rm min}}^{a_{\rm max}} \pi a^2...
...nu) A_{\rm Sil} + Q^{\rm abs}_{\rm C}(a,\nu) A_{\rm C} \big] a^{-3.5} {\rm d}a.$](/articles/aa/full/2001/38/aa1260/img383.gif) |
|
|
(B.7) |
Using the self-similarity of
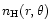 we can integrate
Eq. (B.6) to obtain,
we can integrate
Eq. (B.6) to obtain,
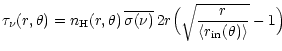 |
|
|
(B.8) |
which was used in Eq. (15). We note that at large
distances from the source, the optical depth converges to a finite
value, proportional to
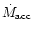 and whose
and whose 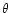 variation is function of the self similar wind solution and central
source radiation field. Thus for high accretion rates, although the
central source radiation hardens, the outer zones of the wind
base are less photoionized than for smaller accretion rates.
variation is function of the self similar wind solution and central
source radiation field. Thus for high accretion rates, although the
central source radiation hardens, the outer zones of the wind
base are less photoionized than for smaller accretion rates.


Up: Atomic T Tauri disk winds
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{figb1.epsi} \end{figure}](/articles/aa/full/2001/38/aa1260/Timg353.gif)
![$\displaystyle \overline{\sigma(\nu)_a}=\int_{a_{\rm min}}^{a_{\rm max}} \pi a^2...
...nu) A_{\rm Sil} + Q^{\rm abs}_{\rm C}(a,\nu) A_{\rm C} \big] a^{-3.5} {\rm d}a.$](/articles/aa/full/2001/38/aa1260/img383.gif)