First, local charge neutrality is always achieved. For example, we
achieve a maximum Debye length of
![]() at
the outer radius of the recollimation zone (model C, lowest
at
the outer radius of the recollimation zone (model C, lowest
![]() ).
).
Second, single fluid approximation requires that relative velocity
drifts of all species (![]() ions, electrons, neutrals)
ions, electrons, neutrals)
![]() are smaller than unity. These
drifts are higher for lower accretion rates and at the outer wind base
(due to the decrease in density and velocity, see
Eq. (9)). In Fig. C.1 we present the
worst case for the drift velocities, showing that our jets can
be indeed approximated by single fluid calculations.
are smaller than unity. These
drifts are higher for lower accretion rates and at the outer wind base
(due to the decrease in density and velocity, see
Eq. (9)). In Fig. C.1 we present the
worst case for the drift velocities, showing that our jets can
be indeed approximated by single fluid calculations.
We assumed gas thermalization, which is achieved only if collisional
time-scales between species
![]() are much smaller than the dynamical time-scale
are much smaller than the dynamical time-scale
![]() .
In the collision
network considered here, the longer time-scales involve collisions
with neutrals. However, even in the worst situation (see
Fig. C.1), after the wind base they remain
comfortably below the above dynamical time-scale.
Our dynamical jet solutions were derived within the ideal MHD
framework. This assumption requires that all terms in the right hand
side of the generalized Ohm's law (Eq. (A.11)) are
negligible when compared to the electromotive field
.
In the collision
network considered here, the longer time-scales involve collisions
with neutrals. However, even in the worst situation (see
Fig. C.1), after the wind base they remain
comfortably below the above dynamical time-scale.
Our dynamical jet solutions were derived within the ideal MHD
framework. This assumption requires that all terms in the right hand
side of the generalized Ohm's law (Eq. (A.11)) are
negligible when compared to the electromotive field
![]() .
We consider Ohm's term
.
We consider Ohm's term
![]() ,
Hall's effect
,
Hall's effect
![]() and the ambipolar diffusion
term
and the ambipolar diffusion
term
![]() (effects due to
the electronic pressure gradient are small compared to the Lorentz
force - Hall's term -). In Fig. C.1 we present
the worst case for our ideal MHD checks. We find that deviations
from ideal MHD remain negligible, despite the presence of ambipolar
diffusion. As expected, this is the dominant diffusion process in our
(non turbulent) MHD jets. Ambipolar diffusion is larger for low
accretion rates and at the outer wind base (because the ratio of
the ambipolar to the electromotive term scales as
(effects due to
the electronic pressure gradient are small compared to the Lorentz
force - Hall's term -). In Fig. C.1 we present
the worst case for our ideal MHD checks. We find that deviations
from ideal MHD remain negligible, despite the presence of ambipolar
diffusion. As expected, this is the dominant diffusion process in our
(non turbulent) MHD jets. Ambipolar diffusion is larger for low
accretion rates and at the outer wind base (because the ratio of
the ambipolar to the electromotive term scales as
![]() ).
).
The worst case for the previous three tests is, as expected, for the
model that attains the lowest density: Model C, with the lowest
accretion rate (
![]() )
and at the outer edge footpoint (
)
and at the outer edge footpoint (
![]() ).
).
The dynamical jet evolution was calculated under the additional
assumption of negligible thermal pressure gradient (cold jets). Since
it is the gradient that provides a force, one should not just measure
(along one field line) the relative importance of the gas pressure to
the magnetic pressure (usual
![]() parameter). Instead, we compare the thermal pressure gradient to the
Lorentz force, along (
parameter). Instead, we compare the thermal pressure gradient to the
Lorentz force, along (
![]() )
and perpendicular
(
)
and perpendicular
(
![]() )
to the flow, namely
)
to the flow, namely
| = | 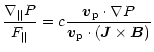 |
(C.1) | |
| = | (C.2) |
In Fig. C.1 we plot the worst case of cold fluid
violation and best case of cold fluid validity. Again the worst case
appears at lower accretion rates and in outer wind zones. It can be
seen that high values of
![]() and
and
![]() can be
attained, hinting at the importance of gas heating on jet dynamics
(providing both enthalpy at the base of the jet and/or pressure
support against recollimation further out). We underline that models
inconsistent with the cold fluid approximation are those found to have
the largest difficulty in meeting the observations
(Paper II). Conversely, models that better reproduce
observations also fulfill the cold fluid approximation. For those
models, the thermal pressure gradient appears to be fairly negligible
with respect to the Lorentz force.
can be
attained, hinting at the importance of gas heating on jet dynamics
(providing both enthalpy at the base of the jet and/or pressure
support against recollimation further out). We underline that models
inconsistent with the cold fluid approximation are those found to have
the largest difficulty in meeting the observations
(Paper II). Conversely, models that better reproduce
observations also fulfill the cold fluid approximation. For those
models, the thermal pressure gradient appears to be fairly negligible
with respect to the Lorentz force.
The first ignored process is the term
![]() .
This term decreases for increasing accretion rate and
.
This term decreases for increasing accretion rate and
![]() due to the lower ionizations found in these regions. It is
plotted in Fig. C.2 for the worst case (model C,
due to the lower ionizations found in these regions. It is
plotted in Fig. C.2 for the worst case (model C,
![]() and
and
![]() AU). There, it reaches at most
AU). There, it reaches at most ![]() 13% of
13% of
![]() .
Typical values for higher accretion rates are
only
.
Typical values for higher accretion rates are
only ![]() 0.1% of
0.1% of
![]() .
.
Next we consider heating/cooling of the gas by collision with dust
grains, given by Hollenbach & McKee (1979):
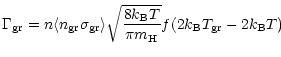 |
(C.3) |
| (C.4) |
Heating due to cosmic rays, which could be important in the outer
tenuous zones of the wind is (Spitzer & Tomasko 1968),
| (C.5) |
Formally, our temperature integration is an initial value problem. In the absence of a self-consistent description of the disc thermodynamics, there is some freedom in the initial temperature determination. It is therefore crucial to check that the subsequent thermal evolution of the wind does not depend critically on the adopted initial value.
Safier obtained the initial temperature by assuming
the poloidal velocity at the slow magnetosonic point (
![]() )
to be the sound speed for adiabatic perturbations
)
to be the sound speed for adiabatic perturbations
![]() .
Here, we have chosen
to compute the initial temperature assuming local thermal equilibrium
.
Here, we have chosen
to compute the initial temperature assuming local thermal equilibrium
![]() .
Our method produces lower initial temperatures than
Safier due to adiabatic cooling.
.
Our method produces lower initial temperatures than
Safier due to adiabatic cooling.
For high accretion rates
![]() our initial temperature versus
our initial temperature versus ![]() has a
minimum at the beginning of the dusty zone: inside the sublimation
cavity, the thermal equilibrium is between photoionization heating and
adiabatic cooling. Just beyond the dust sublimation radius,
photoionization heating is strongly reduced, but the ionization
fraction is still too high for efficient drag heating, resulting in a
low initial equilibrium temperature.
has a
minimum at the beginning of the dusty zone: inside the sublimation
cavity, the thermal equilibrium is between photoionization heating and
adiabatic cooling. Just beyond the dust sublimation radius,
photoionization heating is strongly reduced, but the ionization
fraction is still too high for efficient drag heating, resulting in a
low initial equilibrium temperature.
The initial ionization fraction is similarly determined by assuming
local ionization equilibrium
![]() for all elements. It
decreases with
for all elements. It
decreases with ![]() .
For
.
For
![]() and
and
![]() AU, the initial ionization
fraction is set to a minimum value by assuming that Na is fully
ionized, which is somewhat arbitrary. However, as gas is lifted up
above the disk plane, the dust opacity decreases and the gas heats up,
so that ionization becomes dominated by other photoionized heavy
species and by protons, all computed self consistently.
AU, the initial ionization
fraction is set to a minimum value by assuming that Na is fully
ionized, which is somewhat arbitrary. However, as gas is lifted up
above the disk plane, the dust opacity decreases and the gas heats up,
so that ionization becomes dominated by other photoionized heavy
species and by protons, all computed self consistently.
In order to check that our results do not depend on the initial temperature, we have run model B for a broad range of initial temperatures. As shown in Fig. C.3), we find that the thermal and ionization evolution quickly becomes insensitive to the initial temperature. If we start with a temperature lower than the local isothermal condition, the dominant adiabatic cooling is strongly reduced, and the gas strongly heats up, quickly converging to our nominal curve. If we start with a higher initial temperature, adiabatic cooling is stronger, and we have the characteristic dip in the temperature found by Safier. Our choice of initial temperature has the advantage of reducing this dip, which is somewhat artificial (see Fig. C.3). In either case, we conclude that our results are robust with respect to the choice of initial temperature. In particular, the distance at which the hot plateau is reached, which has a crucial effect on line profile predictions, is unaffected.
Copyright ESO 2001