A precise disk wind theory must explain how much matter is deviated from radial to vertical motion, as well as the amount of energy and angular momentum carried away. This implies a thorough treatment of both the disk interior and its matching with the jets, namely to consider magnetized accretion-ejection structures (hereafter MAES). The only way to solve such an entangled problem is to take into account all dynamical terms, a task that can be properly done within a self-similar framework.
In this paper, we use the models of Ferreira (1997) describing
steady-state, axisymmetric MAES under the following assumptions: (i) a
large scale magnetic field of bipolar topology is threading a
geometrically thin disk; (ii) its ionization is such that MHD applies
(neutrals are well-coupled to the magnetic field); (iii) some active
turbulence inside the disk produces anomalous diffusion allowing
matter to cross the field lines. Two extra simplifying assumptions
were used: (iv) jets are assumed to be cold, i.e. powered by the
magnetic Lorentz force only (the centrifugal force is due to the
Lorentz azimuthal torque), with isothermal magnetic surfaces (the
midplane temperature varying as
![]() )
and (v) jets
carry away all disk angular momentum. This last assumption has been
removed only recently by Casse & Ferreira (2000a).
)
and (v) jets
carry away all disk angular momentum. This last assumption has been
removed only recently by Casse & Ferreira (2000a).
All solutions obtained so far display the same asymptotic behavior. After an opening of the jet radius leading to a very efficient acceleration of the plasma, the jet undergoes a refocusing towards the axis (recollimation). All self-similar solutions are then terminated, most probably producing a shock (Gomez de Castro & Pudritz 1993; Ouyed & Pudritz 1993). This systematic behavior could well be imposed by the self-similar geometry itself and not be a general result (Ferreira 1997). Nevertheless, such a shock would occur in the asymptotic region, far away from the disk. Thus, we can confidently use these solutions in the acceleration zone, where forbidden emission lines are believed to be produced (Hartigan et al. 1995).
The isothermal self-similar MAES considered here are described with
three free dimensionless local parameters (see Ferreira 1997, for more
details) and four global quantities:
(1) the disk aspect ratio
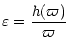 |
(1) |
| (2) |
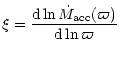 |
(3) |
For our present study, we keep only ![]() and
and
![]() as
free parameters and fix the values of the other five as follows: The
disk aspect ratio was measured by Burrows et al. (1996) for HH 30 as
as
free parameters and fix the values of the other five as follows: The
disk aspect ratio was measured by Burrows et al. (1996) for HH 30 as ![]() 0.1
so we fix
0.1
so we fix
![]() .
The MHD turbulence parameter is
taken
.
The MHD turbulence parameter is
taken
![]() in order to have powerful jets
(Ferreira 1997). The stellar mass is fixed at
in order to have powerful jets
(Ferreira 1997). The stellar mass is fixed at
![]() ,
typical for T Tauri stars, and the inner radius of the MAES
is set to
,
typical for T Tauri stars, and the inner radius of the MAES
is set to
![]() 0.07 AU (typical disk corotation radius
for a 10 days rotation period): inside this region the magnetic field
topology could be significantly affected by the stellar
magnetosphere-disk interaction. The outer radius is kept at
0.07 AU (typical disk corotation radius
for a 10 days rotation period): inside this region the magnetic field
topology could be significantly affected by the stellar
magnetosphere-disk interaction. The outer radius is kept at
![]() for consistency with the one fluid
approximation (Appendix C) and the atomic gas description.
Regarding atomic consistency, Safier (1993a) solved the flow
evolution assuming inicially all H bound in H2. He found H2 to
completely dissociate at the wind base, for small
for consistency with the one fluid
approximation (Appendix C) and the atomic gas description.
Regarding atomic consistency, Safier (1993a) solved the flow
evolution assuming inicially all H bound in H2. He found H2 to
completely dissociate at the wind base, for small ![]() .
However, after a critical flow line footpoint H2 would not
completely dissociate, therefore affecting the thermal solution. This
critical footpoint was at 3 AU for his MHD solution nearer our
parameter space.
.
However, after a critical flow line footpoint H2 would not
completely dissociate, therefore affecting the thermal solution. This
critical footpoint was at 3 AU for his MHD solution nearer our
parameter space.
We note that our two free parameters are still bounded by
observational constraints: mass conservation relates the ejection
index ![]() to the accretion/ejection rates ratios,
to the accretion/ejection rates ratios,
| (4) |
Table 1 provides a list of some disk and jet parameters.
These local parameters were constrained by steady-state requirements,
namely the smooth crossing of MHD critical points. Disk parameters are
useful to give us a view of the physical conditions inside the disk.
Thus, the required magnetic field B0 at the disk midplane and at a
radial distance ![]() is
is
| (6) |
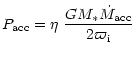 |
= | 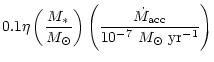 |
|
| (7) |
| Solution |
|
|
||||
| A | 0.010 | 0.729 | 1.46 | 0.014 | 41.6 | 50.6 |
| B | 0.007 | 0.690 | 1.46 | 0.011 | 59.4 | 52.4 |
| C | 0.005 | 0.627 | 1.52 | 0.009 | 84.2 | 55.4 |
In order to obtain a solution for the MAES, a variable separation
method has been used allowing to transform the set of coupled
partially differential equations into a set of coupled ordinary
differential equations (ODEs). Hence, the solution in the
![]() space is obtained by solving for a flow line and then scaling this
solution to all space. Once a solution is found (for a given set of
parameters in Sect. 2.2), the evolution of all wind
quantities Q along any flow line is given by:
space is obtained by solving for a flow line and then scaling this
solution to all space. Once a solution is found (for a given set of
parameters in Sect. 2.2), the evolution of all wind
quantities Q along any flow line is given by:
| (8) |
Copyright ESO 2001