

Up: Atomic T Tauri disk winds
Subsections
Appendix A: Multicomponent MHD equations
A.1 Single fluid description
Let us consider a fluid composed of 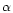 species of numerical
density
species of numerical
density 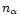 ,
mass
,
mass 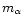 ,
charge
,
charge 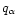 and velocity
and velocity
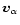 .
All species are assumed to be coupled enough so that
they have the same temperature T. To get a single fluid description,
we then define
.
All species are assumed to be coupled enough so that
they have the same temperature T. To get a single fluid description,
we then define
as being the flow density 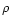 ,
velocity
,
velocity 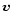 ,
pressure P and
current density
,
pressure P and
current density 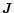 .
We consider now a fluid composed of three
species, namely electrons (e), ions (i) and neutrals (n). The
equations of motion for each species are
.
We consider now a fluid composed of three
species, namely electrons (e), ions (i) and neutrals (n). The
equations of motion for each species are
where
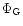 is the gravitational potential and the collisional
force of particles
is the gravitational potential and the collisional
force of particles 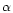 on particles
on particles 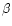 is given by
is given by
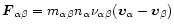 ,
,
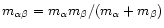 being the reduced mass,
being the reduced mass,
 the
collisional frequency and
the
collisional frequency and
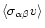 the averaged
momentum transfer rate coefficient.
the averaged
momentum transfer rate coefficient.
A single fluid dynamical description of several species is relevant
whenever they are efficiently collisionally coupled, namely if they
fulfill
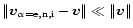 .
Under
this assumption and using Newton's principle (
.
Under
this assumption and using Newton's principle (
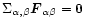 ), we get the usual MHD momentum
conservation equation for one fluid
), we get the usual MHD momentum
conservation equation for one fluid
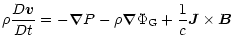 |
|
|
(A.5) |
by adding all equations for each specie. The Lorentz force acting on
the mean flow is
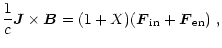 |
|
|
(A.6) |
where
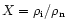 .
Even if the bulk of the flow is neutral,
collisions with charged particles give rise to magnetic effects. In
turn, the magnetic field is coupled to the flow by the currents
generated there. This feedback is provided by the induction equation,
which requires the knowledge of the local electric field
.
Even if the bulk of the flow is neutral,
collisions with charged particles give rise to magnetic effects. In
turn, the magnetic field is coupled to the flow by the currents
generated there. This feedback is provided by the induction equation,
which requires the knowledge of the local electric field
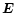 .
Its expression is obtained from the electrons momentum
equation
.
Its expression is obtained from the electrons momentum
equation
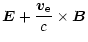 |
= |
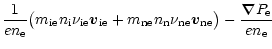 |
(A.7) |
where
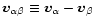 is
the drift velocity between the two species. Due to their negligible
contribution to the mass of the bulk flow, all terms involving the
electrons inertia have been neglected (electrons quite instantly
adjust themselves to the other forces).
is
the drift velocity between the two species. Due to their negligible
contribution to the mass of the bulk flow, all terms involving the
electrons inertia have been neglected (electrons quite instantly
adjust themselves to the other forces).
All drift velocities can be easily obtained. The electron-ion drift
velocity is directly provided by
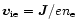 .
Using Eq. (A.6) and noting that
.
Using Eq. (A.6) and noting that
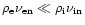 we get the ion-neutral drift velocity
we get the ion-neutral drift velocity
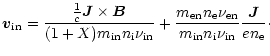 |
|
|
(A.8) |
On the same line of thought, the electrons velocity is
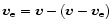 where
where
Gathering these expressions for all drift velocities, we obtain the
generalized Ohm's law
where
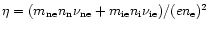 is the electrical resistivity due to collisions. The corresponding MHD heating rate writes
is the electrical resistivity due to collisions. The corresponding MHD heating rate writes
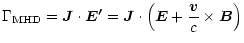 |
|
|
(A.12) |
where 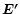 is the electrical field in the comoving frame. This
expression leads to Eq. (17).
is the electrical field in the comoving frame. This
expression leads to Eq. (17).
The generalization of this derivation for a mixture of several
chemical elements has been done in a quite straightforward way. The
bulk flow density becomes
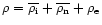 ,
where the overline stands for a sum over all elements
(ions and neutrals), with
,
where the overline stands for a sum over all elements
(ions and neutrals), with
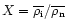 .
The neutrals and ions velocities are means over all elements,
.
The neutrals and ions velocities are means over all elements,
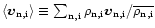 .
The conductivity and collision
terms are also sums over all elements, namely
.
The conductivity and collision
terms are also sums over all elements, namely
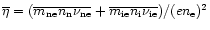 and
and
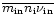 ,
and are computed using the expressions for the collision frequencies.
,
and are computed using the expressions for the collision frequencies.
A.2 Momentum transfer rate coefficient
For ion-electron collisions we use the canonical from
Schunk (1975), summed over all species:
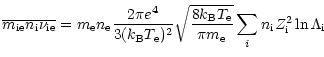 |
|
|
(A.13) |
with the Coulomb factor
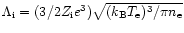 .
.
For the collisions between electrons and neutrals we use the
expression of Osterbrock (1961) for the collisional momentum
transfer rate coefficient between a neutral and a charged particle,
which corrects the classical one (e.g., Schunk 1975) for strong
repulsive forces at close distances. Its expression is
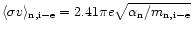 ,
where the
polarizabilities
,
where the
polarizabilities
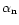 used are also taken from Osterbrock. We
thus obtain
used are also taken from Osterbrock. We
thus obtain
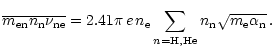 |
|
|
(A.14) |
Finally, it is mainly the ion-neutral collision momentum transfer rate
coefficient determines the ambipolar diffusion heating. It can be
computed with the previous momentum transfer rate coefficient
expression. However as noted by Draine (1980) the previous
expression underestimates 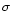 at high velocities. Thus, as
Draine, we take the "hard sphere'' value for the cross-section
(
at high velocities. Thus, as
Draine, we take the "hard sphere'' value for the cross-section
(
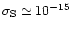 cm2) whenever it is superior to the
polarizability one. For intermediate to hight ionizations
(
cm2) whenever it is superior to the
polarizability one. For intermediate to hight ionizations
(
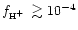 )
the dominant ion-neutral
collisions are those between H-H+. Charge exchange effects between
these two species will amplify
)
the dominant ion-neutral
collisions are those between H-H+. Charge exchange effects between
these two species will amplify
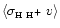 above the values expected by polarizability alone and thus it is
computed separately (Eqs. (A.16) and (A.17)).
We thus obtain for ion-neutral collisions
above the values expected by polarizability alone and thus it is
computed separately (Eqs. (A.16) and (A.17)).
We thus obtain for ion-neutral collisions
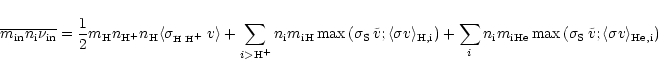 |
(A.15) |
where
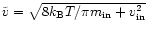 .
For
.
For
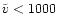 kms-1.
kms-1.
The value of
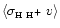 which we used is
given by Draine (1980),
which we used is
given by Draine (1980),
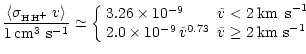 |
|
|
(A.16) |
Safier (1993a) used the expression
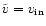 which, as
discussed in Sect. 4.8, results in a smaller momentum transfer rate
coefficient. Geiss & Buergi (1986) computed another expression of the
H-H+ momentum transfer rate coefficient, which provides
which, as
discussed in Sect. 4.8, results in a smaller momentum transfer rate
coefficient. Geiss & Buergi (1986) computed another expression of the
H-H+ momentum transfer rate coefficient, which provides
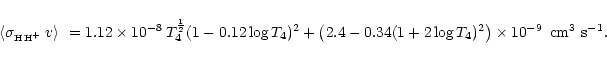 |
(A.17) |
In Fig. 8 we compared both momentum transfer rate
coefficients, they typically differ in 40%, which can be used as an
estimate of their accuracy. It is thus the uncertainty in the H-H+momentum transfer rate coefficient that dominates the final intrinsic
uncertainty of our calculations.


Up: Atomic T Tauri disk winds
Copyright ESO 2001
![]() species of numerical
density
species of numerical
density ![]() ,
mass
,
mass ![]() ,
charge
,
charge ![]() and velocity
and velocity
![]() .
All species are assumed to be coupled enough so that
they have the same temperature T. To get a single fluid description,
we then define
.
All species are assumed to be coupled enough so that
they have the same temperature T. To get a single fluid description,
we then define
![]() .
Under
this assumption and using Newton's principle (
.
Under
this assumption and using Newton's principle (
![]() ), we get the usual MHD momentum
conservation equation for one fluid
), we get the usual MHD momentum
conservation equation for one fluid
![]() .
Using Eq. (A.6) and noting that
.
Using Eq. (A.6) and noting that
![]() we get the ion-neutral drift velocity
we get the ion-neutral drift velocity
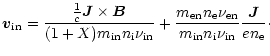
![]() ,
where the overline stands for a sum over all elements
(ions and neutrals), with
,
where the overline stands for a sum over all elements
(ions and neutrals), with
![]() .
The neutrals and ions velocities are means over all elements,
.
The neutrals and ions velocities are means over all elements,
![]() .
The conductivity and collision
terms are also sums over all elements, namely
.
The conductivity and collision
terms are also sums over all elements, namely
![]() and
and
![]() ,
and are computed using the expressions for the collision frequencies.
,
and are computed using the expressions for the collision frequencies.
![]() ,
where the
polarizabilities
,
where the
polarizabilities
![]() used are also taken from Osterbrock. We
thus obtain
used are also taken from Osterbrock. We
thus obtain
![]() which we used is
given by Draine (1980),
which we used is
given by Draine (1980),