In this section we present the calculated thermal and ionization
structure along wind flow lines, discuss the physical origin of the
temperature plateau and its connection with the underlying MHD
solution, discuss the effect of various key model parameters and
finally compare our results with those found by
Safier. The parameters spanned for the calculation of
the thermal solutions are the wind ejection index ![]() describing the
flow line geometry, the mass accretion rate
describing the
flow line geometry, the mass accretion rate
![]() and
the cylindrical radius
and
the cylindrical radius ![]() where the field is anchored in the
disk.
where the field is anchored in the
disk.
In Fig. 2, solid curves present the out of ionization
equilibrium evolution of temperature, electronic density, and proton
fraction along flow lines with
![]() and 1 AU, as a
function of
and 1 AU, as a
function of
![]() ,
for accretion rates ranging from
10-8 to
,
for accretion rates ranging from
10-8 to
![]() yr-1. For comparison
purposes, dashed curves plot the same quantities calculated assuming
ionization equilibrium at the local temperature and radiation field.
For compactness we present only these detailed results for our model
B, with an intermediate ejection index
yr-1. For comparison
purposes, dashed curves plot the same quantities calculated assuming
ionization equilibrium at the local temperature and radiation field.
For compactness we present only these detailed results for our model
B, with an intermediate ejection index
![]() .
We divide the
flow in three regions: the base, the jet and the recollimation zone.
These regions are separated by the Alfvén point and the
recollimation point (where the axial distance reaches its maximum).
We only present the initial part of the recollimation zone here,
because the dynamical solution is less reliable further out, where gas
pressure is increased by compression and may not be negligible
anymore. Note that the recollimation zone was not yet reached over
the scales of interest in the solutions used by
Safier.
.
We divide the
flow in three regions: the base, the jet and the recollimation zone.
These regions are separated by the Alfvén point and the
recollimation point (where the axial distance reaches its maximum).
We only present the initial part of the recollimation zone here,
because the dynamical solution is less reliable further out, where gas
pressure is increased by compression and may not be negligible
anymore. Note that the recollimation zone was not yet reached over
the scales of interest in the solutions used by
Safier.
The gas temperature increases steeply at the wind base (after an
initial cooling phase for high
![]() yr-1). It then stabilizes in a hot temperature
plateau around
yr-1). It then stabilizes in a hot temperature
plateau around ![]() 1-3
1-3
![]() K, before increasing again
after the recollimation point through compressive heating. The plateau
is reached further out for larger accretion rates and larger
K, before increasing again
after the recollimation point through compressive heating. The plateau
is reached further out for larger accretion rates and larger
![]() .
Its temperature decreases with increasing
.
Its temperature decreases with increasing
![]() .
The temperature plateau and its behavior with
.
The temperature plateau and its behavior with
![]() were first identified by Safier in his wind
solutions. We will discuss in Sect. 4.4 why they
represent a robust property of magnetically-driven disk winds heated
by ambipolar diffusion.
were first identified by Safier in his wind
solutions. We will discuss in Sect. 4.4 why they
represent a robust property of magnetically-driven disk winds heated
by ambipolar diffusion.
The bottom panels of Fig. 2 plot the proton fraction
![]() along the flow lines. It rises
steeply with wind temperature through collisional ionization, reaching
a value
along the flow lines. It rises
steeply with wind temperature through collisional ionization, reaching
a value
![]() at the beginning of the temperature plateau.
Beyond this point, it continues to increase but starts to "lag
behind'' the ionization equilibrium calculations (dashed curves): the
density decline in the expanding wind increases the ionization and
recombination timescales. Eventually, for
at the beginning of the temperature plateau.
Beyond this point, it continues to increase but starts to "lag
behind'' the ionization equilibrium calculations (dashed curves): the
density decline in the expanding wind increases the ionization and
recombination timescales. Eventually, for
![]() ,
density
is so low that these timescales become longer than the dynamical ones,
and the proton fraction becomes completely "frozen-in'' at a constant
level, typically a factor 2-3 below the value found in ionization
equilibrium calculations (dashed curves).
,
density
is so low that these timescales become longer than the dynamical ones,
and the proton fraction becomes completely "frozen-in'' at a constant
level, typically a factor 2-3 below the value found in ionization
equilibrium calculations (dashed curves).
The electron density (![]() )
evolution is shown in the middle
panels of Fig. 2. In the jet region, where
)
evolution is shown in the middle
panels of Fig. 2. In the jet region, where ![]() is roughly constant, the dominant decreasing pattern with
is roughly constant, the dominant decreasing pattern with ![]() is
set by the wind density evolution as the gas speeds up and
expands. Similarly, the rise in
is
set by the wind density evolution as the gas speeds up and
expands. Similarly, the rise in ![]() in the recollimation zone
is due to gas compression. A remarkable result is that, as long as
ionization is dominated by hydrogen (i.e.
in the recollimation zone
is due to gas compression. A remarkable result is that, as long as
ionization is dominated by hydrogen (i.e.
![]() ),
), ![]() is not highly dependent of
is not highly dependent of
![]() ,
increasing by a factor of 10 only over three orders in magnitude in
accretion rate. This indicates a roughly inverse scaling of
,
increasing by a factor of 10 only over three orders in magnitude in
accretion rate. This indicates a roughly inverse scaling of ![]() with
with
![]() (bottom panels of Fig. 2),
a property already found by Safier which we will
discuss in more detail later.
(bottom panels of Fig. 2),
a property already found by Safier which we will
discuss in more detail later.
In regions at the wind base where
![]() ,
variations
of
,
variations
of ![]() are linked to the detailed photoionization of heavy
elements which are then the dominant electron donors. The respective
contributions of various ionized heavy atoms to the electronic
fraction
are linked to the detailed photoionization of heavy
elements which are then the dominant electron donors. The respective
contributions of various ionized heavy atoms to the electronic
fraction ![]() is illustrated in Fig. 3 for
is illustrated in Fig. 3 for
![]() yr-1. While
O II and N II are strongly coupled to hydrogen
collisional ionization through charge exchange reactions, the other
elements are dominated by photoionization. The sharp discontinuity in
C II and Na II at the wind base for
yr-1. While
O II and N II are strongly coupled to hydrogen
collisional ionization through charge exchange reactions, the other
elements are dominated by photoionization. The sharp discontinuity in
C II and Na II at the wind base for
![]() AU
is caused by the crossing of the dust sublimation surface by the
streamline (see Appendix B). Inside the surface we are in
the dust sublimation zone where heavy atoms are consequently not
depleted onto grains and hence have a higher abundance. In contrast,
for
AU
is caused by the crossing of the dust sublimation surface by the
streamline (see Appendix B). Inside the surface we are in
the dust sublimation zone where heavy atoms are consequently not
depleted onto grains and hence have a higher abundance. In contrast,
for
![]() AU, the flow starts already outside the
sublimation radius, in a region well-shielded from the UV flux of the
boundary-layer, where only Na is ionized. Extinction progressively
decreases as material is lifted above the disk plane and sulfur, then
carbon, also become completely photoionized.
AU, the flow starts already outside the
sublimation radius, in a region well-shielded from the UV flux of the
boundary-layer, where only Na is ionized. Extinction progressively
decreases as material is lifted above the disk plane and sulfur, then
carbon, also become completely photoionized.
The heating and cooling terms along the streamlines for our out of
equilibrium calculations are plotted in Fig. 4 for
![]() and 1 AU, and for two values of
and 1 AU, and for two values of
![]() = 10-6 and
= 10-6 and
![]() yr-1.
yr-1.
Before the recollimation point, the main cooling process throughout
the flow is adiabatic cooling
![]() ,
although Hydrogen
line cooling
,
although Hydrogen
line cooling
![]() is definitely not
negligible. The main heating process is ambipolar diffusion
is definitely not
negligible. The main heating process is ambipolar diffusion
![]() .
The only exception occurs at the wind base for
small
.
The only exception occurs at the wind base for
small
![]() 0.1 AU and large
0.1 AU and large
![]() yr-1, where photoionization heating
yr-1, where photoionization heating
![]() initially dominates. Under such conditions,
ambipolar diffusion heating is low due to the high ion density, which
couples them to neutrals and reduces the drift responsible for drag
heating. However,
initially dominates. Under such conditions,
ambipolar diffusion heating is low due to the high ion density, which
couples them to neutrals and reduces the drift responsible for drag
heating. However,
![]() decays very fast due to the
combined effects of radiation dilution, dust opacity, depletion of
heavy atoms in the dust phase, and the decrease in gas density. At the
same time, the latter two effects make
decays very fast due to the
combined effects of radiation dilution, dust opacity, depletion of
heavy atoms in the dust phase, and the decrease in gas density. At the
same time, the latter two effects make
![]() rise and
become quickly the dominant heating term. In the recollimation zone,
the main cooling process is hydrogen line cooling
rise and
become quickly the dominant heating term. In the recollimation zone,
the main cooling process is hydrogen line cooling
![]() ,
and the main heating term is compression heating
(
,
and the main heating term is compression heating
(
![]() is negative).
is negative).
A striking result in Fig. 4, also found by
Safier, is that a close match is quickly established
along each streamline between
![]() and
and
![]() ,
and is maintained until the recollimation region. The value of
,
and is maintained until the recollimation region. The value of
![]() where this balance is established is also where the temperature
plateau starts. We will demonstrate below why this is so for the
class of MHD wind solutions considered here.
where this balance is established is also where the temperature
plateau starts. We will demonstrate below why this is so for the
class of MHD wind solutions considered here.
The existence of a hot temperature plateau where
![]() exactly balances
exactly balances
![]() is the most remarkable and robust
property of magnetically-driven disk winds heated by ambipolar
diffusion. Furthermore, it occurs throughout several decades along
the flow including the zone of the jet that current observations are
able to spatially resolve.
is the most remarkable and robust
property of magnetically-driven disk winds heated by ambipolar
diffusion. Furthermore, it occurs throughout several decades along
the flow including the zone of the jet that current observations are
able to spatially resolve.
In this section, we explore in detail which generic properties of our
MHD solution allow a temperature plateau at
![]() K to be
reached, and why this equilibrium may not be reached for other MHD
wind solutions.
K to be
reached, and why this equilibrium may not be reached for other MHD
wind solutions.
First, we note that the energy equation (Eq. (22)) in the
region where drag heating and adiabatic cooling are the dominant terms
(which includes the plateau region) can be cast in the simplified
form:
| (27) |
| |
Figure 5:
Left: function F(T) in erg g cm3 s-1versus temperature assuming local ionization equilibrium and an
ionization flux that ionizes only all Na and all C. Center:
function |
The "wind function'' G is plotted in the center panel of
Fig. 5 for our 3 solutions. It rises by 5 orders of
magnitude at the wind base and then stabilizes in the jet region
(until it diverges to infinity near the recollimation point). The
physical reason for its behavior is better seen if we note that the
main force driving the flow is the Lorentz force:
| (28) |
The "ionization function'' F is in general a rising function of Tand is plotted in the left panel of Fig. 5 under the
approximation of local ionization equilibrium. Two regimes are
present: in the low temperature regime, ![]()
![]() is
dominated by the abundance of photoionized heavy elements and
is
dominated by the abundance of photoionized heavy elements and
![]() increases linearly with T, for fixed
increases linearly with T, for fixed ![]() .
The effect of the UV flux in this region is to shift vertically
F(T): for a low UV flux regime only Na is ionized and
.
The effect of the UV flux in this region is to shift vertically
F(T): for a low UV flux regime only Na is ionized and
![]() ;
for a high UV flux regime were Carbon is
fully ionized,
;
for a high UV flux regime were Carbon is
fully ionized,
![]() .
In the high
temperature regime (
.
In the high
temperature regime (
![]() K) where hydrogen collisional
ionization dominates,
K) where hydrogen collisional
ionization dominates, ![]()
![]() ,
and
,
and
![]() becomes a steeply rising function of
temperature, until hydrogen is fully ionized around
becomes a steeply rising function of
temperature, until hydrogen is fully ionized around
![]() K. The following second rise in F(T) is due to Helium
collisional ionization. As we go out of perfect local ionization
equilibrium the effect is to decrease the slope of F(T) in the region
where H ionization dominates. In the extreme situation of ionization
freezing, F(T) becomes linear again as in the photoionized region:
K. The following second rise in F(T) is due to Helium
collisional ionization. As we go out of perfect local ionization
equilibrium the effect is to decrease the slope of F(T) in the region
where H ionization dominates. In the extreme situation of ionization
freezing, F(T) becomes linear again as in the photoionized region:
![]() .
.
The plateau is simply a region where the temperature does not vary
much,
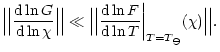 |
(32) |
Finally, a third constraint is that the flow must quickly reach
the plateau solution
![]() and tend to maintain
this equilibrium. Let us assume that
and tend to maintain
this equilibrium. Let us assume that
![]() is fulfilled at
is fulfilled at
![]() ,
what will be the temperature at
,
what will be the temperature at
![]() ?
Letting
?
Letting
![]() and assuming
and assuming
![]() ,
Eq. (24) gives us
,
Eq. (24) gives us
![]() ,
which
provides an exponential convergence towards
,
which
provides an exponential convergence towards
![]() as long as
as long as
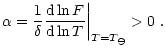 |
(33) |
We conclude that three analytical criteria must be met by any MHD wind
dominated by ambipolar diffusion heating and adiabatic cooling, in
order to converge to a hot temperature plateau:
(1) Equilibrium: the wind function G must be such that
![]() is possible around
is possible around
![]() K;
K;
(2) Small temperature variation: the wind function ![]() must vary
slower than the ionization function F(T) such that
must vary
slower than the ionization function F(T) such that
![]() :
(i) the wind must be in ionization
equilibrium, or near it, in regions where G is a fast function of
:
(i) the wind must be in ionization
equilibrium, or near it, in regions where G is a fast function of
![]() ;
(ii) once we have ionization freezing, G must vary slowly,
with
;
(ii) once we have ionization freezing, G must vary slowly,
with
![]() ;
;
(3) Convergence: ![]() ,
i.e.
,
i.e.
![]() ,
which
is always verified for an atomic and expanding wind.
,
which
is always verified for an atomic and expanding wind.
Not all types of MHD wind solutions will verify our first criterion.
Physically, the large values of ![]() observed in our solutions
indicates that there is still a non-negligible Lorentz force after the
Alfvén surface. In this region (which we call the jet) the Lorentz
force is dominated by its poloidal component which both collimates and
accelerates the gas (Fig. 1). The gas acceleration
translates in a further decrease in density contributing to a further
increase in G. Models that provide most of the flow acceleration
before the Alfvén surface might turn out to have a lower wind
function
observed in our solutions
indicates that there is still a non-negligible Lorentz force after the
Alfvén surface. In this region (which we call the jet) the Lorentz
force is dominated by its poloidal component which both collimates and
accelerates the gas (Fig. 1). The gas acceleration
translates in a further decrease in density contributing to a further
increase in G. Models that provide most of the flow acceleration
before the Alfvén surface might turn out to have a lower wind
function ![]() ,
not numerically compatible with the steep portion
of the ionization function F(T). These models would not establish a
temperature plateau around 104 K by ambipolar diffusion
heating. They would either stabilize on a lower temperature plateau
(on the linear part of F(T)) if our second criterion is verified, or
continue to cool if G varies too fast for the second criterion to
hold. This is the case in particular for the analytical wind models
considered by Ruden et al. (1990), where the drag force was computed a
posteriori from a prescribed velocity field. The G function for
their parameter space (Table 3 of Ruden et al.) peaks at
,
not numerically compatible with the steep portion
of the ionization function F(T). These models would not establish a
temperature plateau around 104 K by ambipolar diffusion
heating. They would either stabilize on a lower temperature plateau
(on the linear part of F(T)) if our second criterion is verified, or
continue to cool if G varies too fast for the second criterion to
hold. This is the case in particular for the analytical wind models
considered by Ruden et al. (1990), where the drag force was computed a
posteriori from a prescribed velocity field. The G function for
their parameter space (Table 3 of Ruden et al.) peaks at
![]() erg g cm3 s-1 at
erg g cm3 s-1 at
![]() and then rapidly
decreases as
and then rapidly
decreases as
![]() for higher radii. This translates
into a cooling wind without a plateau.
for higher radii. This translates
into a cooling wind without a plateau.
| |
Figure 6:
Verification of the plateau scalings (Eq. (34)).
Left: we plot the measured
|
The balance between drag heating and adiabatic cooling
(Eq. (30)) can further be used to understand the scalings of
the plateau temperature
![]() and proton fraction
and proton fraction
![]() with the accretion rate
with the accretion rate
![]() and flow line
footpoint radius (
and flow line
footpoint radius (![]() ). In the plateau region, ionization is
intermediate, i.e., sufficiently high to be dominated by protons but
with most of the Hydrogen neutral. Under these conditions we have
). In the plateau region, ionization is
intermediate, i.e., sufficiently high to be dominated by protons but
with most of the Hydrogen neutral. Under these conditions we have
![]() .
On the other hand,
self-similar disk wind models display
.
On the other hand,
self-similar disk wind models display
![]() (Eq. (26)). Therefore,
we expect
(Eq. (26)). Therefore,
we expect
To predict how much of this scaling will be absorbed by
![]() and how much by
and how much by
![]() ,
Safier
considered the ionization equilibrium approximation: for the
temperature range of the plateau (
,
Safier
considered the ionization equilibrium approximation: for the
temperature range of the plateau (![]() K)
K)
![]()
![]() is a very fast varying function of T that can be
approximated as
is a very fast varying function of T that can be
approximated as
![]() with
with ![]() .
One predicts
that
.
One predicts
that
![]() while
while
![]() .
Hence, the inverse scaling
with (
.
Hence, the inverse scaling
with (
![]() )
should be mostly absorbed by
)
should be mostly absorbed by
![]() ,
while the plateau temperature is only weakly
dependent on these parameters. This is verified in the right panel of
Fig. 6, where
,
while the plateau temperature is only weakly
dependent on these parameters. This is verified in the right panel of
Fig. 6, where
![]() in ionization
equilibrium is plotted as a function of
in ionization
equilibrium is plotted as a function of
![]() .
The predicted scaling is
indeed closely followed.
.
The predicted scaling is
indeed closely followed.
Let us now turn back to the actual out-of-equilibrium calculations.
At the base of the flow we find that the wind evolves roughly in
ionization equilibrium (see Fig. 2), however at a
certain point the ionization fraction freezes at values that are near
those of the ionization equilibrium zone. This effect implies that the
ionization fraction should roughly scale as the ionization equilibrium
values at the upper wind base. This in indeed observed in
Fig. 6. This memory of the ionization equilibrium
values by ![]() (as observed in the solar wind by Owocki et al.
1983) is the reason why the scalings of
(as observed in the solar wind by Owocki et al.
1983) is the reason why the scalings of
![]() with (
with (
![]() )
remain correct. We
computed for our solutions the scalings and found for model B:
)
remain correct. We
computed for our solutions the scalings and found for model B:
![]() ,
,
![]() ,
,
![]() and no dependence of
T on
and no dependence of
T on ![]() ,
confirming the memory effect on the ionization
fraction only.
,
confirming the memory effect on the ionization
fraction only.
Finally, we note that for accretion rates in excess of a few times
![]() yr-1, the hot plateau should not be present
anymore: Because of its inverse scaling with
yr-1, the hot plateau should not be present
anymore: Because of its inverse scaling with
![]() ,
the wind function G remains below 10-47 erg g cm3 s-1, and F = G occurs below 104 K, on the linear
low-temperature part of F(T) where
,
the wind function G remains below 10-47 erg g cm3 s-1, and F = G occurs below 104 K, on the linear
low-temperature part of F(T) where
![]() (see Fig. 5). These colder jets will presumably be
partly molecular. Interestingly, molecular jets have only been
observed so far in embedded protostars with high accretion rates
(e.g. Gueth & Guilloteau 1999).
(see Fig. 5). These colder jets will presumably be
partly molecular. Interestingly, molecular jets have only been
observed so far in embedded protostars with high accretion rates
(e.g. Gueth & Guilloteau 1999).
The importance of the underlying MHD solution is illustrated in
Fig. 5. The ejection index ![]() is directly linked
to the mass loaded in the jet (
is directly linked
to the mass loaded in the jet (![]() ,
see Table 1 and
Ferreira 1997). Thus a higher
,
see Table 1 and
Ferreira 1997). Thus a higher ![]() translates in an stronger
adiabatic cooling because more mass is being ejected. The ambipolar
diffusion heating is less sensitive to the ejection index, because the
density increase is balanced by a stronger magnetic field. Hence, the
wind function
translates in an stronger
adiabatic cooling because more mass is being ejected. The ambipolar
diffusion heating is less sensitive to the ejection index, because the
density increase is balanced by a stronger magnetic field. Hence, the
wind function ![]() decreases with increasing
decreases with increasing ![]() .
As a result,
the plateau temperature and ionization fraction also decrease (see
Eq. (34)).
.
As a result,
the plateau temperature and ionization fraction also decrease (see
Eq. (34)).
In Fig. 7 we summarize our results for the three
models by plotting the plateau
![]() versus
versus
![]() ,
for several
,
for several
![]() (values of
(values of ![]() are connected together). In this plane, our MHD solutions lie in a
well-defined "strip'' located below the ionization equilibrium curve,
between the two dotted curves. For a given model, as
are connected together). In this plane, our MHD solutions lie in a
well-defined "strip'' located below the ionization equilibrium curve,
between the two dotted curves. For a given model, as
![]() increases, the plateau ionization fraction and the temperature
both decrease, as expected from the scalings discussed above, moving
the model to the lower-left of the strip. Increasing the ejection
index decreases
increases, the plateau ionization fraction and the temperature
both decrease, as expected from the scalings discussed above, moving
the model to the lower-left of the strip. Increasing the ejection
index decreases ![]() ,
and it can be seen that this has a similar
effect as increasing
,
and it can be seen that this has a similar
effect as increasing
![]() (Eq. (34)).
(Eq. (34)).
In our calculations we take into account depletion of heavy species
into the dust phase. We ran our model with and without depletion and
found these effects to be minor. Changes are only found when
![]() .
The temperature without depletion is
slightly reduced (the higher ionization fraction reduces
.
The temperature without depletion is
slightly reduced (the higher ionization fraction reduces
![]() )
and as a consequence
)
and as a consequence
![]() is also
smaller. Normally these changes affect only the wind base, as the
temperature increases
is also
smaller. Normally these changes affect only the wind base, as the
temperature increases
![]() dominates the ionization and we
obtain the same results for the plateau zone. However for high
accretion rates (
dominates the ionization and we
obtain the same results for the plateau zone. However for high
accretion rates (
![]() )
in the outer wind zone (large
)
in the outer wind zone (large ![]() )
we still
have
)
we still
have
![]() for the plateau and thus the
temperature without depletion is reduced there.
for the plateau and thus the
temperature without depletion is reduced there.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{fig8.epsi} %
\end{figure}](/articles/aa/full/2001/38/aa1260/Timg284.gif) |
Figure 8:
|
The most striking difference between our results and those of
Safier is an ionization fraction 10 to 100 times
smaller. This difference is mainly due to both different
![]() momentum transfer rate coefficients
and dynamical MHD wind models.
momentum transfer rate coefficients
and dynamical MHD wind models.
The critical importance of the momentum transfer rate coefficient
(
![]() )
for the plateau ionization fraction
can be seen by repeating the reasoning in the previous section but
including the momentum transfer rate coefficient in the scalings. We
thus obtain
)
for the plateau ionization fraction
can be seen by repeating the reasoning in the previous section but
including the momentum transfer rate coefficient in the scalings. We
thus obtain
| (35) |
Copyright ESO 2001