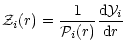 |
(A.1) |
Here, we introduce a technique which allows to investigate the properties of the eigen-solutions of a formally self-adjoint differential equation, which was been developed initially, to analyze the properties of the solutions of the Sturm-Liouville problem (Prüfer 1926). This method is convenient to find out how often the solution of Eq. (29) (corresponding to both descriptions), oscillates in the interval under consideration, which corresponds to the number of zeros of that solution.
The linear adiabatic wave equation of
stellar oscillations (Eq. (29)),
is written as a system of two differential equations of
first-order. This is accomplished by the transformation
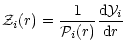 |
(A.1) |
| (A.3) |
We point out that the transformation of the standard
differential equation into a self-adjoint form
does not conserve necessarily the number of zeros or the location of the original
differential equation. The same remains true for all the transformations
between equivalent differential equations.
However, under the two transformations presented previously
to the differential Eq. (4),
the self-adjoint transformation and the phase transformation,
the number and the location of zeros of the wave function ![]() are preserved. In the case of the self-adjoint form it is necessary
to take the convenient formulation, for which the function
are preserved. In the case of the self-adjoint form it is necessary
to take the convenient formulation, for which the function
![]() ,
does not presents zeros in the interval, where the self-adjoint form
is applied.
,
does not presents zeros in the interval, where the self-adjoint form
is applied.
Furthermore, we point out that the number of zeros of a given eigenfunction is not a unique way to classify modes (see Sect. 5). In fact, a classification scheme can be determined independent of that and the number of zeros can be used to classify the modes only in some particular cases.
A solution
![]() of the Eq. (29) has a zero at a point
r=r1 if and only if
of the Eq. (29) has a zero at a point
r=r1 if and only if
![]() ,
where n is always
an integer.
At each of these points
,
where n is always
an integer.
At each of these points
![]() and
and
![]() .
On the propagation regions where
.
On the propagation regions where
![]() ,
this means geometrically that each curve
,
this means geometrically that each curve
![]() in the plane
in the plane
![]() ,
corresponding to a solution
,
corresponding to a solution
![]() of the differential Eq. (29)
(for a given eigenvalue
of the differential Eq. (29)
(for a given eigenvalue ![]() ), can cross the
), can cross the
![]() axis
(
axis
(
![]() )
counterclockwise when
)
counterclockwise when
![]() ,
and
clockwise when
,
and
clockwise when
![]() .
The solution
.
The solution
![]() of the Eq. (29)
(or equivalently of the Eq. (A.6)) for a
given interval can lead to one of two possible
cases:
If sgn
of the Eq. (29)
(or equivalently of the Eq. (A.6)) for a
given interval can lead to one of two possible
cases:
If sgn
![]() then it has a discrete number of zeros, if any at all.
Alternatively, if
sgn
then it has a discrete number of zeros, if any at all.
Alternatively, if
sgn
![]() then it has either one zero or no zero at all.
The waves are propagative only, where
sgn
then it has either one zero or no zero at all.
The waves are propagative only, where
sgn
![]() and they are evanescent elsewhere.
In the case of the acoustic propagative region
(
and they are evanescent elsewhere.
In the case of the acoustic propagative region
(
![]() and
and
![]() )
the phase is increasing with the radius
(
)
the phase is increasing with the radius
(
![]() )
and
in the case of gravity propagative region (
)
and
in the case of gravity propagative region (
![]() and
and
![]() )
the phase
is decreasing with the radius (
)
the phase
is decreasing with the radius (
![]() ).
In case of pure acoustic modes,
the phase
).
In case of pure acoustic modes,
the phase ![]() is always
increasing (
is always
increasing (
![]() )
in all the interval where the wave is propagative,
and decreasing elsewhere.
This works conversely for the pure gravity modes.
)
in all the interval where the wave is propagative,
and decreasing elsewhere.
This works conversely for the pure gravity modes.
In resume, we can identify a particular phase signature of modes
related with the propagative behavior in a given region. Then
locally a gravity type wave and a acoustic type wave,
propagates
depending upon whether the phase point is
traveling clockwise (gravity or g-modes, where
![]() ),
or counterclockwise (acoustic or p-modes, where
),
or counterclockwise (acoustic or p-modes, where
![]() ),
at points of
),
at points of
![]() ,
as r increases.
The global behavior of the eigenmodes is discussed in the Sect. 3.2.
,
as r increases.
The global behavior of the eigenmodes is discussed in the Sect. 3.2.
Copyright ESO 2001