The stellar oscillations are now described by one or another
phase equations (Eqs. (36) and (37)).
These phase equations with the
respective boundary conditions 44 and 47
or 45 and 48 form a boundary value problem
with ![]() as an eigenvalue.
In this section we start by determining numerically the eigenfrequencies that are solutions
of the eigenvalue problem presented. By the following, we will present a classification
scheme base in the result obtained.
as an eigenvalue.
In this section we start by determining numerically the eigenfrequencies that are solutions
of the eigenvalue problem presented. By the following, we will present a classification
scheme base in the result obtained.
Let's start by observing that the phase function
![]() (mod
(mod ![]() ), has the same
number of zeros at the same location as the wave function
), has the same
number of zeros at the same location as the wave function ![]() ,
provided that
the transformations
are made as was indicated previously.
However, the number and location of the zeros of the wave function,
,
provided that
the transformations
are made as was indicated previously.
However, the number and location of the zeros of the wave function, ![]() ,
(obtained from the equation of motion, Sect. 2), are the same
as
,
(obtained from the equation of motion, Sect. 2), are the same
as ![]() ,
only for pure acoustic or gravity modes, due to the fact that the discriminant fas given by Eq. (10)
is strictly positive or negative in all the star.
In the case of mixed modes, another zero occurs for the wave function,
,
only for pure acoustic or gravity modes, due to the fact that the discriminant fas given by Eq. (10)
is strictly positive or negative in all the star.
In the case of mixed modes, another zero occurs for the wave function,
![]() ,
at the radius of the star where f=0.
,
at the radius of the star where f=0.
The main properties of the stellar oscillations, can be well defined
in a linear phase diagram (see Fig. 4) that determines the
phase dependence of a given eigenmode with the radius, for a given equilibrium structure.
The construction of the linear phase diagram is made by introduction of
an effective phase,
![]() .
This effective phase for each eigenmode, of
an eigenvalue
.
This effective phase for each eigenmode, of
an eigenvalue ![]() and degree l, is given by
and degree l, is given by
| (53) |
The nonradial oscillations of a star
can be interpreted as a superposition of stationary waves
generated by the competition between the pressure and the gravity.
These two driving mechanisms, define the two
propagation regions illustrated in the Fig. 3
for a polytropic equilibrium structure of index
![]() .
An eigenstate, can be interpreted heuristically as being
the result of the competition between these two propagative regions,
as it is determined by the phase Eq. (36)
(or Eq. (37)).
The eigenstates corresponding to the acoustic waves of high frequency,
can be determined neglecting the contribution of the
gravity propagation region (which corresponds to neglecting
the second term of Eq. (36),
which case is similar to the Sturm-Liouville problem.
In this case, the modes form a well-ordered sequence,
starting from a given fundamental state.
Conversely, the eigenstates of gravity waves of very low frequency,
can be determined by neglecting the contribution of the acoustic propagation.
A particular state occurs in the star, even in a very simple
equilibrium structure, caused by the fact
that both propagative regions contribute in the same order of magnitude
for this standing wave. This corresponds to the f-mode. Furthermore,
this eigenmode presents a mixed nature and propagates mainly or uniquely
in the evanescent region of the star.
Cowling (1941) was the first to point out
the fundamental difference of nature of the f-mode,
relatively to the p-modes and g-modes.
The f-mode corresponds to the fundamental oscillation of the system for
which no nodes occur on the wavefunction.
Furthermore, for stars where mixing of modes can occur, this
f-mode, as it is defined here, cannot exist.
.
An eigenstate, can be interpreted heuristically as being
the result of the competition between these two propagative regions,
as it is determined by the phase Eq. (36)
(or Eq. (37)).
The eigenstates corresponding to the acoustic waves of high frequency,
can be determined neglecting the contribution of the
gravity propagation region (which corresponds to neglecting
the second term of Eq. (36),
which case is similar to the Sturm-Liouville problem.
In this case, the modes form a well-ordered sequence,
starting from a given fundamental state.
Conversely, the eigenstates of gravity waves of very low frequency,
can be determined by neglecting the contribution of the acoustic propagation.
A particular state occurs in the star, even in a very simple
equilibrium structure, caused by the fact
that both propagative regions contribute in the same order of magnitude
for this standing wave. This corresponds to the f-mode. Furthermore,
this eigenmode presents a mixed nature and propagates mainly or uniquely
in the evanescent region of the star.
Cowling (1941) was the first to point out
the fundamental difference of nature of the f-mode,
relatively to the p-modes and g-modes.
The f-mode corresponds to the fundamental oscillation of the system for
which no nodes occur on the wavefunction.
Furthermore, for stars where mixing of modes can occur, this
f-mode, as it is defined here, cannot exist.
It is possible to prove that
the modes form a well-ordered sequence when the star is
simple![]() ,
given that two different eigenmodes never cross.
However, this can be guaranteed only for modes that propagate locally as an
acoustic type wave or
gravity type wave. The evanescent type mode f is the only exception.
The fact that the phase of two eigenmodes never crosses, is reliable on the topological
properties of the propagation diagram
(see Figs. 1, 2 and 3)
and the properties
of the phase equations. For two waves with frequencies,
,
given that two different eigenmodes never cross.
However, this can be guaranteed only for modes that propagate locally as an
acoustic type wave or
gravity type wave. The evanescent type mode f is the only exception.
The fact that the phase of two eigenmodes never crosses, is reliable on the topological
properties of the propagation diagram
(see Figs. 1, 2 and 3)
and the properties
of the phase equations. For two waves with frequencies, ![]() and
and ![]() ,
such as
,
such as
![]() ,
the propagative characteristics
are fixed differently for an acoustic-gravity wave,
in function of the type of propagation.
For a wave that propagates acoustically,
the higher frequency presents always a larger propagative
region.
Conversely, for a wave that propagates by gravity type,
the higher frequency presents always a smaller propagative
region. Furthermore, on the propagative region, we have that
,
the propagative characteristics
are fixed differently for an acoustic-gravity wave,
in function of the type of propagation.
For a wave that propagates acoustically,
the higher frequency presents always a larger propagative
region.
Conversely, for a wave that propagates by gravity type,
the higher frequency presents always a smaller propagative
region. Furthermore, on the propagative region, we have that
![]() ,
for two waves that propagate acoustically,
and
,
for two waves that propagate acoustically,
and
![]() ,
on the other cases.
Using the phase equations corresponding
to each one of these descriptions,
we have that
,
on the other cases.
Using the phase equations corresponding
to each one of these descriptions,
we have that
![]() for acoustic type propagation
and
for acoustic type propagation
and
![]() for gravity type propagation, for each point inside the star.
This determines that two eigenmodes can never cross each other,
if they are acoustic waves, gravity waves or mixed waves.
for gravity type propagation, for each point inside the star.
This determines that two eigenmodes can never cross each other,
if they are acoustic waves, gravity waves or mixed waves.
In Figs. 3 and 4
we represent the propagation
diagram and the linear phase diagram for the eigenmodes of degree l,
for a polytropic equilibrium structure of index
![]() and adiabatic index
and adiabatic index
![]() .
The phase function of acoustic waves and gravity waves,
present important propagative topological differences between them.
However, for the very low frequency acoustic waves and high frequency
gravity waves, the propagation is similar to a f-mode.
.
The phase function of acoustic waves and gravity waves,
present important propagative topological differences between them.
However, for the very low frequency acoustic waves and high frequency
gravity waves, the propagation is similar to a f-mode.
The main asymptotic properties can be illustrated in
the planar approximation (see Appendix B).
In the case of acoustic modes, corresponding to the higher frequencies
(
![]() ), the
phase Eq. (36) is dominated by the term
), the
phase Eq. (36) is dominated by the term ![]() ,
through the discriminant
,
through the discriminant ![]() and
and ![]() .
Then the phase,
.
Then the phase, ![]() ,
is given approximatively by
,
is given approximatively by
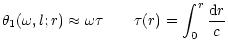 |
(54) |
Alternatively, the gravity modes
are given by Eq. (37), corresponding to the smaller frequencies
(
![]() ),
the discriminants
),
the discriminants ![]() and
and ![]() can be approximated by
can be approximated by
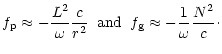 |
(55) |
In the example presented above, mixing of modes does not occur (no overlap of the propagative region), but if this happens, the phase function presents a similar behaviour to the acoustic and gravity modes for each one of the respective propagation regions (see Fig. 2b).
Copyright ESO 2001