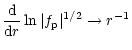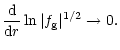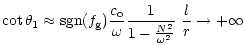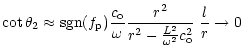Up: Nonradial adiabatic oscillations of
Appendix B: Determination of the boundary conditions in the case of planar approximation
In this section, we present the calculation of the endpoints conditions of
the associated phase system, applied to equations of motion for adiabatic oscillations
when the wavelength is much less than the solar radius, the local effects of spherical
geometry on the dynamic can be ignored (Deubner & Gough 1984,
see also Sect. 2.1.1).
To simplify the determination of the
endpoints of the phase equations, from the
boundary conditions (see Sect. 2.2), we will
consider the phase equations, on the approximation proposed in Sect. 3.4
(Eqs. (51) and (52)).
Furthermore, we will consider only the dominant terms for
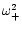 and
and
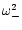 in the planar approximation, given by Eq. (26),
which are proportional to
in the planar approximation, given by Eq. (26),
which are proportional to
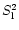 and N2, respectively.
This example is particularly interesting
because the boundary conditions corresponding to that case remain the same
for the other approximations by the fact that the dominant terms
which determine the local behaviour of the phase are
presented in this case. The functions,
and N2, respectively.
This example is particularly interesting
because the boundary conditions corresponding to that case remain the same
for the other approximations by the fact that the dominant terms
which determine the local behaviour of the phase are
presented in this case. The functions, 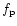 and
and 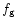 are given approximately by
are given approximately by
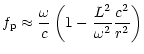 |
|
|
(B.1) |
and
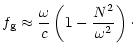 |
|
|
(B.2) |
The boundary condition, of the 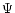 function, can be determined
from the boundary conditions of
function, can be determined
from the boundary conditions of 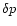 ,
by the Eq. (6)
and the respective boundary conditions for
,
by the Eq. (6)
and the respective boundary conditions for 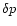 .
The regularity condition in the centre for
.
The regularity condition in the centre for 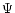 is
is
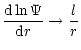 |
|
|
(B.3) |
as
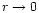 .
The boundary condition on the surface, for
.
The boundary condition on the surface, for 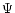 is
is
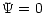 |
|
|
(B.4) |
at r=R.
Using the phase transformation (Eq. (A.5)),
![$\displaystyle \cot{\theta_i}
={\rm sgn}({\cal M}_i)\vert{\cal M}_i\vert^{2}\lef...
...r}\ln{\vert{\cal M}_i\vert}
+ \frac{\rm d}{{\rm d}r}\ln{\vert\Psi\vert} \right]$](/articles/aa/full/2001/27/aah2247/img233.gif) |
|
|
(B.5) |
for each one of the descriptions i=1,2.
We observe that for the centre, from the series expansions of equilibrium quantities
we obtain (as
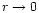 ),
),
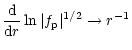 |
|
|
(B.6) |
and
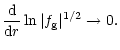 |
|
|
(B.7) |
Under these considerations,
it is possible to determine the initial phase of the associated phase system.
The endpoints for the centre are (
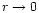 ).
In the case of the acoustic description, we obtain
).
In the case of the acoustic description, we obtain
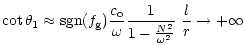 |
|
|
(B.8) |
or
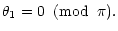 |
|
|
(B.9) |
In the case of the gravity description, we obtain
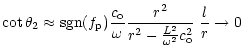 |
|
|
(B.10) |
or
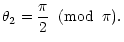 |
|
|
(B.11) |
The endpoints for the surface, can also be calculated for both descriptions.
It is also possible to determine the amplitude boundary conditions,
but they are not interesting to our problem.
At last, it is important to observe that the initial boundary conditions
can be understood in terms of the physical nature of the acoustic
and gravity waves.


Up: Nonradial adiabatic oscillations of
Copyright ESO 2001
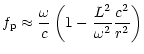
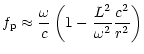
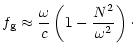
![$\displaystyle \cot{\theta_i}
={\rm sgn}({\cal M}_i)\vert{\cal M}_i\vert^{2}\lef...
...r}\ln{\vert{\cal M}_i\vert}
+ \frac{\rm d}{{\rm d}r}\ln{\vert\Psi\vert} \right]$](/articles/aa/full/2001/27/aah2247/img233.gif)