- ...
problem
![[*]](/icons/foot_motif.gif)
- Strictly speaking, this is not a Sturm-Liouville
problem because the dependence of the eigenvalue with the equilibrium
model is rather complicated. However, the main properties
of this oscillatory system are quite similar
to the classical Sturm-Liouville problem.
This has been put in evidence by Ledoux & Walraven (1958)
for the high order gravity modes and the high order acoustic modes,
where a second-order system of stellar oscillations has been
obtained under the Cowling approximation
(see Sect. 3.4).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
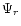
![[*]](/icons/foot_motif.gif)
- Hereafter
we will refer to
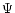 as
as 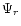 ,
if not stated otherwise.
,
if not stated otherwise.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... conjugates
![[*]](/icons/foot_motif.gif)
- We observe that if
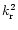 is real,
then
is real,
then
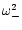 and
and
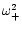 are both real or
complex conjugates.
Consequently
are both real or
complex conjugates.
Consequently 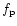 and
and 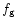 are also complex conjugate functions.
are also complex conjugate functions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... invariant
![[*]](/icons/foot_motif.gif)
- In this context,
invariant means that the different differential equations,
that can be obtained by any type of transformation
(of the independent and dependent variables or both),
has
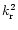 as a characteristic quantity, independent of the transformation considered.
as a characteristic quantity, independent of the transformation considered.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
simple
![[*]](/icons/foot_motif.gif)
- A star is considered simple in this context: when its propagation
diagram can be obtained by a topological deformation of a simple polytrope such
as polytrope
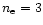 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... phase
![[*]](/icons/foot_motif.gif)
- For some modes the influence of
the boundary conditions is negligible. In those cases
only the layers of the evanescent region, very near the turning
point,
contribute to the phase. Such cases,
correspond to consider that the endpoints of the problem
are:
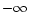 and
and 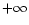 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sequence
![[*]](/icons/foot_motif.gif)
-
by "well-ordered sequence'' we mean that two modes of
different frequencies never cross.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.