All Tables
- Table 1:
Initial models and their parametrisation:
A and
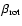 are the rotation law parameter
(Eq. (12)) and the ratio of rotational to
gravitational energy, respectively. Larger values of A correspond
to more rigidly rotating cores.
are the rotation law parameter
(Eq. (12)) and the ratio of rotational to
gravitational energy, respectively. Larger values of A correspond
to more rigidly rotating cores. 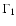 is the sub-nuclear
adiabatic index of our hybrid equation of state (see
Sect. 2.2).
is the sub-nuclear
adiabatic index of our hybrid equation of state (see
Sect. 2.2).
- Table 2:
Parametrisation of the initial
magnetic fields for the models of series AaBbGg-DdMm by the radius
of the field generating current loop centered at
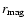 (parametrized by
d = 1, 2, 3, 4, 0) and the field strength in the
core's center
(parametrized by
d = 1, 2, 3, 4, 0) and the field strength in the
core's center
 (parametrized by
m = 10, 11,
12, 13). For models AaBbGg-D0Mm the field generating current loop
is located at infinity yielding a uniform magnetic field throughout
the entire core.
(parametrized by
m = 10, 11,
12, 13). For models AaBbGg-D0Mm the field generating current loop
is located at infinity yielding a uniform magnetic field throughout
the entire core.
- Table 3:
Initial magnetic energy
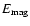 and typical values of the ratio of magnetic to
gravitational energy
and typical values of the ratio of magnetic to
gravitational energy
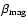 (the exact values depend
also on the hydrodynamic initial model and its gravitational energy)
for the models of series AaBbGg-DdM12. The magnetic energy of models
with
(the exact values depend
also on the hydrodynamic initial model and its gravitational energy)
for the models of series AaBbGg-DdM12. The magnetic energy of models
with
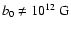 can be obtained by a simple
scaling relation, e.g.
can be obtained by a simple
scaling relation, e.g.
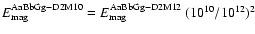 .
.
- Table D.1:
Some characteristic model quantities: the first two columns give the model name and the
classification of the GW signal (for the corresponding
non-magnetized model). Columns 3 and 4 give the time of bounce
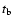 (in milliseconds) and the maximum density at bounce
(in milliseconds) and the maximum density at bounce
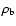 (in units of
(in units of
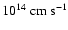 ). An exclamation mark behind the density value signifies that the maximum density of
the model exceeds the bounce density during the later evolution.
). An exclamation mark behind the density value signifies that the maximum density of
the model exceeds the bounce density during the later evolution.
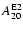 (Col. 5) and
(Col. 5) and
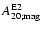 (Col. 6) are the maximum GW amplitude (in cm) and
the corresponding magnetic contribution.
(Col. 6) are the maximum GW amplitude (in cm) and
the corresponding magnetic contribution.
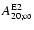 (Col. 7) is a rough mean value of the wave
amplitude (in cm) at some late epoch; no value is provided when the
GW amplitude does not approach a quasi-constant asymptotic value.
If the absolute value of this amplitude is large, the presence of an aspheric outflow at late epochs can be inferred. The following columns give the maximum value of the rotational (Col. 8) and the magnetic beta parameter (Col. 9), the time when
(Col. 7) is a rough mean value of the wave
amplitude (in cm) at some late epoch; no value is provided when the
GW amplitude does not approach a quasi-constant asymptotic value.
If the absolute value of this amplitude is large, the presence of an aspheric outflow at late epochs can be inferred. The following columns give the maximum value of the rotational (Col. 8) and the magnetic beta parameter (Col. 9), the time when
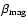 reaches its maximum (Col. 10), and the corresponding beta of the toroidal field (Col. 11). If the
magnetic field is still amplifying at the end of the simulation, an exclamation mark is added behind the table entry, and if the magnetic field is decreasing at this time, we give its final
value
reaches its maximum (Col. 10), and the corresponding beta of the toroidal field (Col. 11). If the
magnetic field is still amplifying at the end of the simulation, an exclamation mark is added behind the table entry, and if the magnetic field is decreasing at this time, we give its final
value
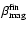 in parentheses.
in parentheses.
- Table D.2:
Some characteristic model quantities (name of model given in Col. 1) at time t (in
msec; Col. 2) when the core has reached a quasi-equilibrium
state. For models which do not reach a quasi-equilibrium state
until the end of the simulation (e.g. type-II models with large
scale core pulsations) we provide upper (top value) and lower
(bottom value) bounds estimated from the values at maximum and
minimum contraction. Columns 3 and 4 give the surface radius
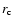 (in km) and the mass
(in km) and the mass
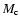 (in solar masses) of the quasi-equilibrium configuration, respectively.
Since it is still surrounded by an (expanding) envelope of high
density matter, the definition of its surface radius
(in solar masses) of the quasi-equilibrium configuration, respectively.
Since it is still surrounded by an (expanding) envelope of high
density matter, the definition of its surface radius
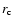 is somewhat uncertain. As the rotation rate
is somewhat uncertain. As the rotation rate
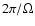 (in ms), where
(in ms), where 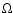 is the angular velocity
averaged over the angle
is the angular velocity
averaged over the angle 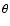 ,
as well as the total magnetic
field
,
as well as the total magnetic
field 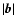 and (the absolute value of) its toroidal component
and (the absolute value of) its toroidal component
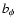 (both in Gauss) vary strongly near the surface and on short time scales, the corresponding values in Cols. 5-7 should be used with care. Negative values of the rotation
rate signify counter-rotating cores. Finally, in Cols. 8 and 9
we give the radii of the shock at the polar axis,
(both in Gauss) vary strongly near the surface and on short time scales, the corresponding values in Cols. 5-7 should be used with care. Negative values of the rotation
rate signify counter-rotating cores. Finally, in Cols. 8 and 9
we give the radii of the shock at the polar axis,
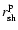 ,
and at the equator,
,
and at the equator,
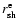 (both in cm), respectively. No entry
in these columns implies that the shock has already left the
computational grid.
(both in cm), respectively. No entry
in these columns implies that the shock has already left the
computational grid.