A&A 450, 1107-1134 (2006)
DOI: 10.1051/0004-6361:20054306
M. Obergaulinger - M. A. Aloy - E. Müller
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching bei München, Germany
Received 5 October 2005 / Accepted 19 December 2005
Abstract
Aims. We have performed a comprehensive parameter study of the collapse of rotating, strongly magnetized stellar cores in axisymmetry to determine their gravitational wave signature based on the Einstein quadrupole formula.
Methods. We use a Newtonian explicit magnetohydrodynamic Eulerian code based on the relaxing-TVD method for the solution of the ideal MHD equations, and apply the constraint-transport method to guarantee a divergence-free evolution of the magnetic field. We neglect effects due to neutrino transport and employ a simplified equation of state. The initial models are polytropes in rotational equilibrium with a prescribed degree of differential rotation and rotational energy. The initial magnetic fields are purely poloidal the field strength ranging from
![]() to
to
![]() .
The evolution of the core is followed until a few ten milliseconds past core bounce.
.
The evolution of the core is followed until a few ten milliseconds past core bounce.
Results. The initial magnetic fields are amplified mainly by the differential rotation of the core giving rise to a strong toroidal field component with an energy comparable to the rotational energy. The poloidal field component grows by compression during collapse, but does not change significantly after core bounce. In large parts of the simulated cores the growth time of the magneto-rotational instability (MRI) is of the order of a few milliseconds. The saturation field strengths that can be reached both via a pure ![]() dynamo or the MRI are of the order of
dynamo or the MRI are of the order of
![]() at the surface of the core. Sheet-like circulation flows which produce a strong poloidal field component transporting angular momentum outwards develop due to MRI, provided the initial field is not too weak. Weak initial magnetic fields (
at the surface of the core. Sheet-like circulation flows which produce a strong poloidal field component transporting angular momentum outwards develop due to MRI, provided the initial field is not too weak. Weak initial magnetic fields (![]()
![]() )
have no significant effect on the dynamics of the core and the gravitational wave signal. Strong initial fields (
)
have no significant effect on the dynamics of the core and the gravitational wave signal. Strong initial fields (![]()
![]() )
cause considerable angular momentum transport whereby rotational energy is extracted from the collapsed core which loses centrifugal support and enters a phase of secular contraction. The gravitational wave amplitude at bounce changes by up to a few ten percent compared to the corresponding non-magnetic model. If the angular momentum losses are large, the post-bounce model. If the angular momentum losses are large the post-bounce equilibrium state of the core changes from a centrifugally to a pressure supported one. This transition imprints in the gravitational wave signal a reduction of the amplitude of the large-scale oscillations characteristic of cores bouncing due to centrifugal forces.
)
cause considerable angular momentum transport whereby rotational energy is extracted from the collapsed core which loses centrifugal support and enters a phase of secular contraction. The gravitational wave amplitude at bounce changes by up to a few ten percent compared to the corresponding non-magnetic model. If the angular momentum losses are large, the post-bounce model. If the angular momentum losses are large the post-bounce equilibrium state of the core changes from a centrifugally to a pressure supported one. This transition imprints in the gravitational wave signal a reduction of the amplitude of the large-scale oscillations characteristic of cores bouncing due to centrifugal forces.
In some models the quasi-periodic large-scale oscillations are replaced by higher frequency irregular oscillations. This pattern defines a new signal type which we call a type IV gravitational wave signal. Collimated bipolar outflows give rise to a unique feature that may allow their detection by means of gravitational wave astronomy: a large positive quadrupole wave amplitude of similar size as that of the bounce signal.
Key words: magnetohydrodynamics (MHD) - gravitational waves - supernovae: general
The gravitational binding energy liberated by the collapse of the iron
core of a massive (
![]() )
star to a neutron star is the
commonly accepted energy source of type Ib/c and type II supernovae, as
a few percent of this energy are sufficient to unbind and rapidly eject
the stellar envelope and to create the supernova outburst. However,
which physical processes turn the central implosion into the explosion
of the stellar layers surrounding the forming neutron star is still
debated in spite of many efforts over more than three decades. Heating
of stellar gas just outside the proto-neutron star (PNS) by neutrinos
diffusing and being advected out of its interior is thought to play a crucial role in the explosion mechanism. However, as current neutrino-driven supernova models produce (weak) explosions only for low mass progenitors (for a recent review, see e.g. Janka et al. 2004), there may be a need to include additional physics in the models in order to make them work successfully for more massive progenitors, too.
)
star to a neutron star is the
commonly accepted energy source of type Ib/c and type II supernovae, as
a few percent of this energy are sufficient to unbind and rapidly eject
the stellar envelope and to create the supernova outburst. However,
which physical processes turn the central implosion into the explosion
of the stellar layers surrounding the forming neutron star is still
debated in spite of many efforts over more than three decades. Heating
of stellar gas just outside the proto-neutron star (PNS) by neutrinos
diffusing and being advected out of its interior is thought to play a crucial role in the explosion mechanism. However, as current neutrino-driven supernova models produce (weak) explosions only for low mass progenitors (for a recent review, see e.g. Janka et al. 2004), there may be a need to include additional physics in the models in order to make them work successfully for more massive progenitors, too.
On this account magneto-rotational core collapse, which has been studied by a few authors in the past (LeBlanc & Wilson 1970; Symbalisty 1984; Müller & Hillebrandt 1979; Meier et al. 1976; Ohnishi 1983; Bisnovatyi-Kogan et al. 1976), has become an active research field in recent years (Kotake et al. 2004b,a; Wheeler & Akiyama 2004; Akiyama et al. 2003; Takiwaki et al. 2004; Wheeler et al. 2002; Yamada & Sawai 2004; Sawai et al. 2005; Ardeljan et al. 2005; Kotake et al. 2005). Further reasons for this activity are the availability of sufficient computational power for the necessarily multi-dimensional magneto-hydrodynamic (MHD) simulations, observations indicating very asymmetric explosions (Wang et al. 2001,1996; Leonard et al. 2001), and the interpretation of Anomalous X-Ray Pulsars and Soft Gamma-Ray Repeaters as magnetars, i.e. very strongly magnetized neutron stars (Kouveliotou et al. 1999; Duncan & Thompson 1992; Thompson & Duncan 1996).
Concerning the initial conditions for magneto-rotational core collapse
the up to now most advanced evolutionary calculations of rotating
massive stars (Heger et al. 2005) predict that the initial
rotation rates are more than an order of magnitude smaller than (i) the
minimum ones used in past (parameter) studies of magneto-rotational
core collapse, and (ii) those predicted by previous evolutionary
calculations (see,
e.g. Hirschi et al. 2003; Woosley et al. 2002)
which lead to neutron stars rotating very rapidly (![]() 1 ms) at
birth. The latter studies ignored the torques exerted in differentially
rotating regions by the magnetic fields that thread them. Thus, the
stars end up with 30 to 50 times more angular momentum than in the
models by Heger et al. (2005) in that part of their core
destined to collapse to a neutron star.
1 ms) at
birth. The latter studies ignored the torques exerted in differentially
rotating regions by the magnetic fields that thread them. Thus, the
stars end up with 30 to 50 times more angular momentum than in the
models by Heger et al. (2005) in that part of their core
destined to collapse to a neutron star.
The strength (and distribution) of the initial magnetic field in the
stellar core is unknown. If weak initially, several possible
amplification mechanisms exist that may amplify the magnetic field of
the collapsing progenitor to a dynamically important strength. Linear
amplification of the field by means of differential rotation will occur
(Meier et al. 1976), which transforms rotational energy
into magnetic energy by winding up any seed polodial field into a toroidal magnetic field. This process can be accompanied by the action
of meridional (e.g. convective) motions that transform toroidal into
poloidal fields. Both processes together lead to the so-called
![]() -
-![]() dynamo. Recently, the magneto-rotational instability
(MRI) (see Balbus & Hawley 1998) has received a lot of
interest in the context of supernova collapse and explosion
(Yamada & Sawai 2004; Sawai et al. 2005; Kotake et al. 2004a; Akiyama et al. 2003). Unlike linear wrapping, the
MRI will give rise to an exponential growth of the field strength while
working on the same time scale (see however
Sawai et al. 2005). The MRI saturation
field is independent of the initial field, i.e. even quite small
initial fields can be amplified to dynamically important strengths. The
MRI will occur if the radial gradient of the angular velocity is
negative, a condition arising quite naturally in core collapse
situations.
dynamo. Recently, the magneto-rotational instability
(MRI) (see Balbus & Hawley 1998) has received a lot of
interest in the context of supernova collapse and explosion
(Yamada & Sawai 2004; Sawai et al. 2005; Kotake et al. 2004a; Akiyama et al. 2003). Unlike linear wrapping, the
MRI will give rise to an exponential growth of the field strength while
working on the same time scale (see however
Sawai et al. 2005). The MRI saturation
field is independent of the initial field, i.e. even quite small
initial fields can be amplified to dynamically important strengths. The
MRI will occur if the radial gradient of the angular velocity is
negative, a condition arising quite naturally in core collapse
situations.
A major effect of magnetic fields on the collapse dynamics is the
transport of angular momentum. Due to its very low (fluid and ![]() shear) viscosity (see e.g. Keil et al. 1996) a collapsing non-magnetized stellar core maintains its Lagrangian angular momentum profile
shear) viscosity (see e.g. Keil et al. 1996) a collapsing non-magnetized stellar core maintains its Lagrangian angular momentum profile ![]() ,
m being the Lagrangian mass coordinate, on time
scales of
,
m being the Lagrangian mass coordinate, on time
scales of ![]() 1 s, but magnetic fields can significantly
redistribute the angular momentum (Meier et al. 1976).
This can slow down the forming neutron star and thus counteract the
effects of rotation. In some cases, even retrograde rotation may result
in some parts of the core (Müller & Hillebrandt 1979).
Angular momentum transfer can also destabilize the rotational
equilibrium the core resides in after a centrifugal bounce at
sub-nuclear densities, and lead to a subsequent (second) collapse to
nuclear densities and beyond that releases large amounts of
gravitational binding energy (Symbalisty 1984).
Conversely, the violent convective flow both inside the neutrino sphere
and between the neutrino sphere and the shock will transport and amplify
magnetic fields in the collapsed core of a supernova
(Thompson & Murray 2001).
1 s, but magnetic fields can significantly
redistribute the angular momentum (Meier et al. 1976).
This can slow down the forming neutron star and thus counteract the
effects of rotation. In some cases, even retrograde rotation may result
in some parts of the core (Müller & Hillebrandt 1979).
Angular momentum transfer can also destabilize the rotational
equilibrium the core resides in after a centrifugal bounce at
sub-nuclear densities, and lead to a subsequent (second) collapse to
nuclear densities and beyond that releases large amounts of
gravitational binding energy (Symbalisty 1984).
Conversely, the violent convective flow both inside the neutrino sphere
and between the neutrino sphere and the shock will transport and amplify
magnetic fields in the collapsed core of a supernova
(Thompson & Murray 2001).
Analytic considerations (Meier et al. 1976; Wheeler et al. 2002) and numerical simulations (Yamada & Sawai 2004; Symbalisty 1984; Sawai et al. 2005; Ardeljan et al. 2005; Akiyama et al. 2003; LeBlanc & Wilson 1970; Kotake et al. 2004b,a) show that magneto-rotational core collapse might lead to jet-like explosions. Though the magnetic stress will remain below equipartition strength in most regions of the star, it might affect the dynamics of the core through its anisotropic components. Magnetic stresses can assist in pushing the stalled shock, or may even drive a mildly relativistic outflow in form of a jet along the rotation axis, which is powered by the rotational energy transfered to the jet by the magnetic stresses.
Observations of gravitational waves (GWs) will allow one to learn more
about the supernova mechanism as they provide pristine information
directly from the stellar interior, in particular about the amount and
distribution of the angular momentum, and the strength and topology of
the magnetic field. Simplified Newtonian
(Yamada & Sawai 2004; Yamada & Sato 1994; Müller 1982; Kotake et al. 2003; Zwerger & Müller 1997; Kotake et al. 2004b; Mönchmeyer et al. 1991; Ott et al. 2004; Fryer et al. 2004) and general-relativistic
(Dimmelmeier et al. 2002a,b) calculations of rotational core collapse
predict the emission of a strong signal around core bounce, and that the
magnitude of the bounce signal as well as the post-bounce gravitational
radiation depend sensitively on the initial rotation rate and rotation
profile. Newtonian hydrodynamic simulations using more sophisticated
micro- and transport-physics, as well as state-of-the-art rotating
progenitors (Heger et al. 2005) show that the
gravitational wave signal at core bounce is small compared to the signal
produced by convective motions in the post-bounce core and by aspheric
neutrino emission (Müller et al. 2004). Magneto-rotational effects on the gravitational wave signature were
first investigated in detail by
Kotake et al. (2004b) and
Yamada & Sawai (2004) who found differences from
the signature of purely hydrodynamic models only in the case of very
strong initial fields (
![]() ).
).
In the following we present a comprehensive parameter study of the axisymmetric Newtonian core collapse of rotating magnetized polytropes and of their gravitational wave signature. Our study extends the work of Zwerger & Müller (1997) (hereafter ZM) and the complementary work of Dimmelmeier et al. (2002a,b) (hereafter DFM), who investigated the hydrodynamic collapse of a large set of rotating polytropes in Newtonian and general relativistic gravity, respectively. The simulations have been performed with the recently developed MHD difference scheme of Pen et al. (2003). They incorporate neither neutrino transport nor nuclear burning processes. Due to the reduced complexity of our models we could explore many of them covering a large region in parameter space, the focus being the gravitational wave signal emitted by magnetized stellar cores and their dynamic evolution. Because of our assumptions and approximations the validity of our models is limited to the stage of core collapse and to the first few ten milliseconds of their post-bounce evolution.
Several related but less comprehensive numerical MHD studies have been
performed in the past few years:
Yamada & Sawai (2004) used the ZEUS-2D code,
employed the parametric equation of state of
Yamada & Sato (1994), considered no neutrinos, and
followed the evolution of initially rapidly rotating and very strongly
magnetized (
![]() )
cores with a purely
homogeneous poloidal field. Contrary to
LeBlanc & Wilson (1970) and
Symbalisty (1984) they find that the magnetic field
becomes strongest behind the shock wave and not in the inner core, and
thus is the main driving factor of the observed jet outflow along the
rotation axis. Besides a field amplification by differential rotation,
they also observe the possible action of the MRI. They calculate the
gravitational wave signal in the quadrupole approximation finding no
substantial difference between the bounce signal of magnetized and
non-magnetized models. Kotake et al. (2004b)
also use the ZEUS-2D code to which they add an approximate neutrino
cooling with a leakage scheme. They assume an initially predominantly
toroidal magnetic field in their investigated 14 models of which all but
one are very strongly magnetized
)
cores with a purely
homogeneous poloidal field. Contrary to
LeBlanc & Wilson (1970) and
Symbalisty (1984) they find that the magnetic field
becomes strongest behind the shock wave and not in the inner core, and
thus is the main driving factor of the observed jet outflow along the
rotation axis. Besides a field amplification by differential rotation,
they also observe the possible action of the MRI. They calculate the
gravitational wave signal in the quadrupole approximation finding no
substantial difference between the bounce signal of magnetized and
non-magnetized models. Kotake et al. (2004b)
also use the ZEUS-2D code to which they add an approximate neutrino
cooling with a leakage scheme. They assume an initially predominantly
toroidal magnetic field in their investigated 14 models of which all but
one are very strongly magnetized
![]() .
Besides the simplified equation of state of
Yamada & Sato (1994) they also consider two realistic equations of state.
Kotake et al. (2004b) focus their study on the
effect of the magnetic field on the gravitational wave signal, and find
that the gravitational wave amplitudes are lowered by
.
Besides the simplified equation of state of
Yamada & Sato (1994) they also consider two realistic equations of state.
Kotake et al. (2004b) focus their study on the
effect of the magnetic field on the gravitational wave signal, and find
that the gravitational wave amplitudes are lowered by ![]()
![]() for
models with the strongest initial magnetic fields (
for
models with the strongest initial magnetic fields (
![]() ). Kotake et al. (2004a),
Takiwaki et al. (2004), and
Kotake et al. (2005) all using the same
input physics and numerics as
Kotake et al. (2004b) are concerned with the
effects of the magnetic fields on the anisotropic neutrino radiation and
convection, on the propagation of the shock wave, and on the
rotation-induced anisotropic neutrino heating through parity-violating
effects, respectively. Kotake et al. (2004a) find that the
aspherical shapes of the shock and of the neutrino sphere (oblate or
prolate depending on the initial rotation law) are enhanced in the
magnetized models, and that the MRI is expected to develop on the prompt
shock propagation time scale. Takiwaki et al. (2004)
observe the formation of a tightly collimated shock wave along the
rotational axis for strongly magnetized models.
Kotake et al. (2005) find an at most 0.5% change of the neutrino heating rates even in their most strongly
magnetized models (
). Kotake et al. (2004a),
Takiwaki et al. (2004), and
Kotake et al. (2005) all using the same
input physics and numerics as
Kotake et al. (2004b) are concerned with the
effects of the magnetic fields on the anisotropic neutrino radiation and
convection, on the propagation of the shock wave, and on the
rotation-induced anisotropic neutrino heating through parity-violating
effects, respectively. Kotake et al. (2004a) find that the
aspherical shapes of the shock and of the neutrino sphere (oblate or
prolate depending on the initial rotation law) are enhanced in the
magnetized models, and that the MRI is expected to develop on the prompt
shock propagation time scale. Takiwaki et al. (2004)
observe the formation of a tightly collimated shock wave along the
rotational axis for strongly magnetized models.
Kotake et al. (2005) find an at most 0.5% change of the neutrino heating rates even in their most strongly
magnetized models (
![]() ).
Ardeljan et al. (2005) employ a 2D implicit Lagrangian code, a simplified equation of state, and consider energy losses by neutrinos and iron dissociation. They add a magnetic field of quadrupole-like symmetry with an energy of 10-6of the core's gravitational binding energy to the collapsed,
post-bounce differentially rotating, stationary core. The toroidal
field component of this seed field first grows linearly due to
differential rotation, but then starts to amplify exponentially due to
the action of the MRI. The resulting drastic increase of the magnetic
pressure eventually causes an explosion with an energy of 0.6
).
Ardeljan et al. (2005) employ a 2D implicit Lagrangian code, a simplified equation of state, and consider energy losses by neutrinos and iron dissociation. They add a magnetic field of quadrupole-like symmetry with an energy of 10-6of the core's gravitational binding energy to the collapsed,
post-bounce differentially rotating, stationary core. The toroidal
field component of this seed field first grows linearly due to
differential rotation, but then starts to amplify exponentially due to
the action of the MRI. The resulting drastic increase of the magnetic
pressure eventually causes an explosion with an energy of 0.6 ![]() 1051 erg. Finally,
Sawai et al. (2005) extend the work of
Yamada & Sawai (2004) by considering
inhomogeneously magnetized cores mainly in the very strong field regime
(
1051 erg. Finally,
Sawai et al. (2005) extend the work of
Yamada & Sawai (2004) by considering
inhomogeneously magnetized cores mainly in the very strong field regime
(
![]() ), which
may produce magnetars. They find that poloidal magnetic fields which are
initially concentrated toward the rotation axis produce more energetic
explosions and more prolate shocks than cores with an initially uniform
field. A core with an initially quadrupolar field
(Ardeljan et al. 2005) gives
rise to a collimated fast jet (
), which
may produce magnetars. They find that poloidal magnetic fields which are
initially concentrated toward the rotation axis produce more energetic
explosions and more prolate shocks than cores with an initially uniform
field. A core with an initially quadrupolar field
(Ardeljan et al. 2005) gives
rise to a collimated fast jet (![]() ), while a core with a pure
toroidal fields shows no sign of an explosion.
), while a core with a pure
toroidal fields shows no sign of an explosion.
The paper is organized as follows: we will describe the physics included in our models in Sect. 2, and briefly introduce our numerical method in Sect. 3. Our results will be discussed in Sect. 4, and a summary and conclusions of our work will be presented in Sect. 5. In the appendices we provide a brief discussion of the relaxing TVD scheme employed in our numerical code (Appendix A), a presentation of the quadrupole formula used for the extraction of the GW signal (Appendix C), and a compilation of some characteristic properties of all models (Appendix D).
We evolve the density ![]() ,
the velocity
,
the velocity ![]() ,
the total energy
density
,
the total energy
density
![]() (
(
![]() ,
,
![]() ,
and
,
and
![]() are the internal, kinetic, and magnetic energy density,
respectively), and the magnetic field
are the internal, kinetic, and magnetic energy density,
respectively), and the magnetic field ![]() of our models using the
equations of Newtonian ideal magnetohydrodynamics (MHD):
of our models using the
equations of Newtonian ideal magnetohydrodynamics (MHD):
Using the ideal MHD equations, we neglect effects due to the viscosity and the finite conductivity of the gas. This is normally a very good approximation for the stellar interior. However, during core collapse interesting hydrodynamic effects might arise from the inclusion of viscosity, in particular in the case of MHD (Thompson et al. 2004). Non-ideal terms in the induction equation might lead to reconnection of field lines, thus possibly affecting the topology of the field, and might prove important for several kinds of hydromagnetic instabilities (Spruit 1999).
For a Newtonian self-gravitating fluid the source terms fn and qin the MHD momentum (2) and energy (3)
equations are given by
We integrate the MHD equations in spherical coordinates assuming axisymmetry, i.e. we cannot simulate non-axisymmetric instabilities which can occur if the rotation rate exceeds a critical value during core collapse due to angular momentum conservation (Tassoul 1978). Axisymmetry also inhibits the growth of various MHD instabilities (Spruit 1999). We further assume equatorial symmetry in order to reduce the computational costs of a simulation.
We do neither consider nuclear reactions nor neutrino transport, and use a simplified equation of state (EOS). Since neutrinos are thought to play a major role in the revival of the stalled prompt shock, our approach is limited to the collapse, bounce, and shock formation phases when neutrinos are not yet dynamically important. This limitation allows us to focus on a specific, not yet comprehensively studied part of core collapse, namely the influence of MHD effects.
We have used the approximate, analytic EOS of
Janka et al. (1993) in our parameter
study. It is based on a decomposition of the gas pressure P into the
sum of a polytropic part
![]() and a thermal part
and a thermal part
![]() :
:
The polytropic pressure changes only due to adiabatic processes,
i.e. it cannot describe dissipation of kinetic into thermal energy in
shocks. This shock heating is treated by the thermal part of the EOS
which has the form of an ideal gas EOS:
Concerning rotation and magnetic field, the conditions in the stellar core at the onset of collapse are not well constrained. Therefore, we have investigated the evolution of a sufficiently broad set of simplified stellar models. Except for the magnetic field, the initial models are the same as those studied by ZM and DFM.
The initial models are rotating polytropes in hydrostatic equilibrium
constructed with the method of Eriguchi & Müller (1985). They rotate according to the so-called j-constant law (Eriguchi & Müller 1985)
The initial models are calculated using the hybrid EoS (7)
in the "cold'' limit, i.e.
![]() ,
an adiabatic index
,
an adiabatic index
![]() ,
the j-constant rotation law (12), and
with a central density
,
the j-constant rotation law (12), and
with a central density
![]() .
Instead of
.
Instead of ![]() we use the ratio of rotational to gravitational binding energy,
we use the ratio of rotational to gravitational binding energy,
![]() (initially
(initially
![]()
![]()
![]() )
to parametrize the models. The
two-dimensional parameter space
)
to parametrize the models. The
two-dimensional parameter space
![]() is covered
by 4
is covered
by 4 ![]() 5 initial models according to Table 1.
5 initial models according to Table 1.
Table 1:
Initial models and their parametrisation:
A and
![]() are the rotation law parameter
(Eq. (12)) and the ratio of rotational to
gravitational energy, respectively. Larger values of A correspond
to more rigidly rotating cores.
are the rotation law parameter
(Eq. (12)) and the ratio of rotational to
gravitational energy, respectively. Larger values of A correspond
to more rigidly rotating cores. ![]() is the sub-nuclear
adiabatic index of our hybrid equation of state (see
Sect. 2.2).
is the sub-nuclear
adiabatic index of our hybrid equation of state (see
Sect. 2.2).
As
![]() for our initial models, they are only marginally
stable against collapse, which can be triggered by either lowering the
coefficient
for our initial models, they are only marginally
stable against collapse, which can be triggered by either lowering the
coefficient ![]() or the adiabatic index
or the adiabatic index ![]() .
The former
approach mimics the energy consumption due to photo-disintegration of
nuclei, while the reduction of
.
The former
approach mimics the energy consumption due to photo-disintegration of
nuclei, while the reduction of ![]() models the softening of the
EOS due to deleptonisation. We apply the latter method to initiate the
collapse.
models the softening of the
EOS due to deleptonisation. We apply the latter method to initiate the
collapse.
For realistic equations of state
![]() and
and
![]() ,
respectively. Following ZM and DFM we constructed models with five different values of the sub-nuclear
adiabatic index
,
respectively. Following ZM and DFM we constructed models with five different values of the sub-nuclear
adiabatic index ![]() ,
and set
,
and set
![]() (Table 1). The nomenclature of the models also follows
that of ZM and DFM; i.e. model A1B3G5 has a rotation parameter A =
5
(Table 1). The nomenclature of the models also follows
that of ZM and DFM; i.e. model A1B3G5 has a rotation parameter A =
5 ![]()
![]() (A1), a fractional rotational energy
(A1), a fractional rotational energy
![]() (B3), and a sub-nuclear adiabatic index
(B3), and a sub-nuclear adiabatic index
![]() (G5; see Table 1).
(G5; see Table 1).
The magnetic fields of our initial models are calculated from the vector
potential of a circular current loop of radius
![]() in the
equatorial plane (Jackson 1962). The only
non-vanishing component of the magnetic vector potential is
in the
equatorial plane (Jackson 1962). The only
non-vanishing component of the magnetic vector potential is ![]() .
It is given by
.
It is given by
The magnetic field strength in the core's center is normalized by
![]() .
For very small radii (
.
For very small radii (
![]() )
the
field resembles a uniform field parallel to the rotation axis, whereas
at large radii the field lines bend towards the equatorial plane. The
field strength is largest in the interior of the current loop
(Fig. 1).
)
the
field resembles a uniform field parallel to the rotation axis, whereas
at large radii the field lines bend towards the equatorial plane. The
field strength is largest in the interior of the current loop
(Fig. 1).
Table 2 provides an overview of the parametrisation
of the magnetic field. The models are denoted as follows: model A3B3G3-D3M12 is the hydrodynamic initial model A3B3G3 (Sect. 2.3.2) endowed with a magnetic field
generated by a current loop located at a radius of
![]() and a maximum field strength of
and a maximum field strength of
![]() (see Table 2). The initial magnetic energy
(see Table 2). The initial magnetic energy
![]() for models AaBbGg-DdM12 is given in Table 3.
for models AaBbGg-DdM12 is given in Table 3.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4306f01a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg139.gif) |
Figure 1:
The initial magnetic field
configuration of the models of series AaBbGg-D3M13. Besides the
field lines the distribution of the magnetic pressure (color coded)
is displayed.
|
| Open with DEXTER | |
Most simulations were performed using models AaBbGg-D3Mm (
m = 10, 11,
12, 13). Their magnetic field configuration is shown in
Fig. 1. Since the radius of the current loop
(
![]() )
that generates this field
configuration is small compared to the radius of the stellar core
(
)
that generates this field
configuration is small compared to the radius of the stellar core
(
![]() ), the magnetic
energy is highly concentrated in the center of the stellar core. This
is different for models AaBbGg-D0Mm, which posses a homogeneous field
directed along the rotational axis. The magnetic energy of these
"uniform-field'' models is much larger than that of the corresponding
"current-loop'' models AaBbGg-DdMm (
d = 1, 2, 3, 4) due to the
contributions of the outer layers of the core.
), the magnetic
energy is highly concentrated in the center of the stellar core. This
is different for models AaBbGg-D0Mm, which posses a homogeneous field
directed along the rotational axis. The magnetic energy of these
"uniform-field'' models is much larger than that of the corresponding
"current-loop'' models AaBbGg-DdMm (
d = 1, 2, 3, 4) due to the
contributions of the outer layers of the core.
The magnetic field strengths of our initial models are - as in most
studies of magneto-rotational collapse - much higher than those
estimated to exist in realistic stellar cores. Magnetic field strengths
in iron cores probably do not exceed
![]() ,
and the
toroidal field component is expected to be much stronger than the
poloidal one (Heger et al. 2005). However, as such
"weak'' initial fields do not give rise to important dynamic effects on
the time scales under consideration here (unless MRI amplification would
take place; see Sect. 4), and as we want to
investigate the principal effects of magnetic fields on the core
collapse, we consider stronger fields in our parameter study. Weaker
initial fields may lead to similar effects after a longer amplification
phase. Our initial fields are purely toroidal, but they rapidly (within
a fraction of the collapse time scale) develop a strong toroidal component.
,
and the
toroidal field component is expected to be much stronger than the
poloidal one (Heger et al. 2005). However, as such
"weak'' initial fields do not give rise to important dynamic effects on
the time scales under consideration here (unless MRI amplification would
take place; see Sect. 4), and as we want to
investigate the principal effects of magnetic fields on the core
collapse, we consider stronger fields in our parameter study. Weaker
initial fields may lead to similar effects after a longer amplification
phase. Our initial fields are purely toroidal, but they rapidly (within
a fraction of the collapse time scale) develop a strong toroidal component.
Table 2:
Parametrisation of the initial
magnetic fields for the models of series AaBbGg-DdMm by the radius
of the field generating current loop centered at
![]() (parametrized by
d = 1, 2, 3, 4, 0) and the field strength in the
core's center
(parametrized by
d = 1, 2, 3, 4, 0) and the field strength in the
core's center
![]() (parametrized by
m = 10, 11,
12, 13). For models AaBbGg-D0Mm the field generating current loop
is located at infinity yielding a uniform magnetic field throughout
the entire core.
(parametrized by
m = 10, 11,
12, 13). For models AaBbGg-D0Mm the field generating current loop
is located at infinity yielding a uniform magnetic field throughout
the entire core.
Table 3:
Initial magnetic energy
![]() and typical values of the ratio of magnetic to
gravitational energy
and typical values of the ratio of magnetic to
gravitational energy
![]() (the exact values depend
also on the hydrodynamic initial model and its gravitational energy)
for the models of series AaBbGg-DdM12. The magnetic energy of models
with
(the exact values depend
also on the hydrodynamic initial model and its gravitational energy)
for the models of series AaBbGg-DdM12. The magnetic energy of models
with
![]() can be obtained by a simple
scaling relation, e.g.
can be obtained by a simple
scaling relation, e.g.
![]() .
.
During collapse, bounce, and explosion the rapid infall of matter and in particular its more or less abrupt slowdown give rise to strong variations of the matter-density quadrupole moment of any aspheric core. This causes the emission of gravitational radiation.
We calculate the gravitational wave amplitude of the core using the
quadrupole formula in spherical coordinates, and applying the extension
of the formulation of Mönchmeyer et al. (1991, MSMK, hereafter) to the
MHD case due to Kotake et al. (2004b). Our
treatment includes the hydrodynamic, gravitational, and magnetic forces
acting on the fluid. We calculate the quadrupole amplitude
![]() according to the formula (see Appendix C):
according to the formula (see Appendix C):
The radiative quadrupole moment
![]() (Eq. (C.3)) is a measure of the asphericity of the core's density distribution. It is positive for a very prolate core, and
negative in the limit of very oblate cores. Its first time derivative
(Eq. (C.3)) is a measure of the asphericity of the core's density distribution. It is positive for a very prolate core, and
negative in the limit of very oblate cores. Its first time derivative
![]() (Eq. (C.4)) measures the asphericity of the mass-flux and the momentum distribution of the core, and its second time derivative, the quadrupole amplitude
(Eq. (C.4)) measures the asphericity of the mass-flux and the momentum distribution of the core, and its second time derivative, the quadrupole amplitude
![]() ,
is a measure of the asphericity of the forces acting on the fluid. As a rule
of thumb, a prolate mass-flux or a prolate momentum distribution
(e.g. a bipolar jet-like outflow along the rotational axis) gives rise
to a positive value of
,
is a measure of the asphericity of the forces acting on the fluid. As a rule
of thumb, a prolate mass-flux or a prolate momentum distribution
(e.g. a bipolar jet-like outflow along the rotational axis) gives rise
to a positive value of
![]() .
Forces that act on the
core in a way to make it more oblate, such as the centrifugal force that
has its manifestation in the
.
Forces that act on the
core in a way to make it more oblate, such as the centrifugal force that
has its manifestation in the
![]() part of the amplitude, will give rise to a negative contribution to the total amplitude (negative sign of the
part of the amplitude, will give rise to a negative contribution to the total amplitude (negative sign of the
![]() term in Eq. (15)).
term in Eq. (15)).
The different signs of the hydrodynamic and the magnetic contributions
to the amplitude (Eq. (16)) resulting from the different
signs of the hydrodynamic (Reynolds) and the magnetic (Maxwell) stresses
in the MHD flux terms, will - for suited topologies of field and flow - lead to a more or less prominent phase shift between the hydrodynamic
and the magnetic amplitude. If the gravitational wave amplitude
![]() is in phase with the hydrodynamic
amplitude
is in phase with the hydrodynamic
amplitude
![]() (which holds well for many
models, in particular for those with relatively long oscillation
periods; see Sect. 4), the magnetic amplitude
(which holds well for many
models, in particular for those with relatively long oscillation
periods; see Sect. 4), the magnetic amplitude
![]() may be phase shifted with respect to
may be phase shifted with respect to
![]() .
Such a phase shift was observed by Yamada & Sawai (2004).
.
Such a phase shift was observed by Yamada & Sawai (2004).
The MHD equations are integrated using a newly developed Eulerian, finite volume code based on the algorithm devised by Pen et al. (2003). This code employs the relaxing TVD method of Jin & Xin (1995) for the solution of the advection equations and the constraint-transport formulation of Evans & Hawley (1988) to deal with the divergence constraint of the magnetic field.
We have rewritten the original code of Pen et al. in order to adjust for the simulations of stellar core collapse. This included the transformation of the equations from Cartesian to spherical coordinates, the calculation of the gravitational potential, the implementation of the gravitational source terms in the momentum and energy equations, and the implementation of an approximate equation of state for iron core matter. The integration of the fluid equations and of the induction equation is based on a second-order (piecewise-linear) relaxing TVD method. For a short summary of this method see Appendix A. For the time evolution we use an operator-split approach based on a method of lines (LeVeque 1992).
![\begin{figure}
\par\mbox{\includegraphics[width=5.15cm,clip]{4306f02a.eps} \incl...
...{4306f02e.eps} \includegraphics[width=5.15cm,clip]{4306f02f.eps} }
\end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg167.gif) |
Figure 2:
The evolution of the maximum density ( top panels) and the GW amplitude ( bottom panels) of three weak-field models: the standard type-I model A1B3G3-D3M10 ( left panels), the type-II model A2B4G1-D3M10 ( middle panels), and the type-III model A3B3G5-D3M10 ( right panels).
The bottom panels show the total GW amplitude
|
| Open with DEXTER | |
The simulations were performed on a grid of 380 logarithmically spaced
radial zones up to
![]() ,
where
,
where
![]() is the radius of the initial stellar model.
The central resolution was
is the radius of the initial stellar model.
The central resolution was
![]() .
The angular grid consisted of 60 equidistant zones in the domain
.
The angular grid consisted of 60 equidistant zones in the domain
![]() .
This grid resolution has
been chosen after obtaining converged results when running several models at different resolutions. The numerical convergence of our simulations is demonstrated in Appendix B.
.
This grid resolution has
been chosen after obtaining converged results when running several models at different resolutions. The numerical convergence of our simulations is demonstrated in Appendix B.
The stellar models used by us (polytropes) are quite compact
configurations of matter characterized by a sharp transition from a high
density interior to a low density surface layer. Note that this feature
is also seen in sophisticated stellar evolution calculations, which
predict a steep density gradient at the outer edge of the iron core. In
rotating models the transition layer is aspherical and must completely
be contained within the spherical boundary of the numerical grid,
i.e. its numerical treatment requires special care. Grid zones outside
the core are filled with an "atmosphere'' fluid of some prescribed
density
![]() at rest. During collapse the infall of
matter creates a region near the edge of the core where the density
might become so low that numerical problems arise. To overcome these
difficulties, we follow the approach of DFM1 and set the hydrodynamic
variables
at rest. During collapse the infall of
matter creates a region near the edge of the core where the density
might become so low that numerical problems arise. To overcome these
difficulties, we follow the approach of DFM1 and set the hydrodynamic
variables
![]() equal to some prescribed values
equal to some prescribed values
![]() in all zones where
the fluid density falls short of a given threshold
in all zones where
the fluid density falls short of a given threshold
![]() .
In this way the atmosphere can adjust to the (non-spherical) varying shape of the star. We used
.
In this way the atmosphere can adjust to the (non-spherical) varying shape of the star. We used
![]() ,
and set
,
and set
![]() .
From the atmospheric density and velocity one can calculate the energy density
assuming zero thermal energy.
.
From the atmospheric density and velocity one can calculate the energy density
assuming zero thermal energy.
The evolution of the magnetic field is turned off for zones marked as
atmosphere, i.e. ![]() remains constant in the atmosphere consistent
with the assumed zero velocity of the atmosphere gas.
remains constant in the atmosphere consistent
with the assumed zero velocity of the atmosphere gas.
The results of our simulations show that magneto-rotational collapse can be categorized in essence into two limiting cases depending on the strength of the initial magnetic field. If the initial magnetic field is weak, its influence on the dynamics and the gravitational wave emission is negligible during the time scales of our simulations (see Sect. 4.1). The results of the hydrodynamic simulations of ZM and DFM apply in this case without any modification. On the other hand, and not unexpectedly, initially strongly magnetized cores evolve quite differently, as will be discussed in Sect. 4.2. Note that since the MRI acts independently of the strength of the initial magnetic field, the distinction between dynamically negligible and dynamically important fields may be an artificial one resulting from our inability to simulate the MRI for magnetic fields below a certain threshold (see Sect. 4.3). Hence, also initially weak magnetic fields may cause similar dynamical effects as strong ones. The dependence of our results on the initial magnetic field configuration will be discussed in Sect. 4.4, and further information about the temporal evolution of all models is provided in Appendix D.
The gravitational wave signals of initially weakly magnetized cores do
not differ from those obtained by MM, ZM and DFM for the corresponding
non-magnetized initial models, because the magnetic fields never become
dynamically important during the simulations. Consequently, both the
magnetic force contribution to the GW amplitude (see
Sect. 2.4) and the back-reaction of the magnetic
field on the flow are negligible. This "weak-field'' behavior holds
for most models with initial fields of ![]()
![]() .
However, in some models bouncing at relative low central density due to
centrifugally forces (e.g. models A4B5G5-D3M12 and A2B4G1-D3M12) even a field of
.
However, in some models bouncing at relative low central density due to
centrifugally forces (e.g. models A4B5G5-D3M12 and A2B4G1-D3M12) even a field of
![]() does not affect the evolution of the
core significantly. We note that these numbers may change when the
field amplification by the MRI, which works independently of the seed
field strength, is properly simulated (see Sect. 4.3).
does not affect the evolution of the
core significantly. We note that these numbers may change when the
field amplification by the MRI, which works independently of the seed
field strength, is properly simulated (see Sect. 4.3).
Three types of GW signals are distinguished by MM and ZM which they call type-I, type-II, and type-III, respectively. The evolution of three representative weak-field models that emit these different signal types is illustrated in Fig. 2. Although the GW signals are very similar to those of the corresponding non-magnetized cores of ZM, we will discuss them and the underlying dynamics here in some detail for reason of comparison with the GW signals of strongly magnetized cores (see Sect. 4.2).
In the case of a type-I (or standard-type) GW signal (model A1B3G3-D3M10; Fig. 2, left panels), the core
bounces due to the stiffening of the nuclear EOS at supra-nuclear
densities. Pressure waves crossing the inner core stop the infall and
lead to the formation of an outward moving shock wave. Hence, the
typical time scale is roughly given by the sound crossing time of the
inner core at bounce (![]() 1 ms). After bounce the core exhibits
damped oscillations on roughly the same time scale. During collapse,
the GW amplitude is increasingly positive due to the gravity
contribution
1 ms). After bounce the core exhibits
damped oscillations on roughly the same time scale. During collapse,
the GW amplitude is increasingly positive due to the gravity
contribution
![]() which dominates the
hydrodynamic one
which dominates the
hydrodynamic one
![]() .
At bounce the
GW amplitude decreases strongly assuming large negative values, because
the modulus of the centrifugal contribution
.
At bounce the
GW amplitude decreases strongly assuming large negative values, because
the modulus of the centrifugal contribution
![]() becomes very large when the rotational energy approaches its maximum. The oscillations of the core
produce the oscillations of
becomes very large when the rotational energy approaches its maximum. The oscillations of the core
produce the oscillations of
![]() and
hence of the total GW amplitude on the same time scale. As the shock
wave is almost spherical (except for initially very rapidly rotating
cores), the post-bounce GW amplitude is predominantly produced by the
central core with only a modest contribution of the outer layers. The
hydrodynamic contribution
and
hence of the total GW amplitude on the same time scale. As the shock
wave is almost spherical (except for initially very rapidly rotating
cores), the post-bounce GW amplitude is predominantly produced by the
central core with only a modest contribution of the outer layers. The
hydrodynamic contribution
![]() is
dominated by
is
dominated by
![]() .
.
A type-II signal (model A2B4G1-D3M10;
Fig. 2, middle panels) is emitted, if, for an initially sufficiently fast rotation and a sufficiently large degree of differential rotation, the core suffers a bounce due to centrifugal forces before nuclear density is reached. After bounce the core
exhibits several large amplitude oscillations, which are considerably
less damped than in the case of a pressure dominated bounce. The
oscillations are reflected in the GW signal: each time the density
reaches a maximum the GW amplitude becomes strongly negative, while
being positive otherwise. The negative GW amplitude again results from
the enhanced rotational energy during this collapse phase when the inner
core also becomes strongly oblate. The contribution of the
centrifugal-force amplitude
![]() to
the hydrodynamic one
to
the hydrodynamic one
![]() is negligible.
Since much of the dynamics happens at relatively large radii, the GW signal is produced by the whole core. The contribution of the central core is typically negative because of its rotationally flattened, oblate shape, whereas the outer layers contribute to the overall amplitude with
a positive signal due to the prolate shape of the outward propagating
shock wave.
is negligible.
Since much of the dynamics happens at relatively large radii, the GW signal is produced by the whole core. The contribution of the central core is typically negative because of its rotationally flattened, oblate shape, whereas the outer layers contribute to the overall amplitude with
a positive signal due to the prolate shape of the outward propagating
shock wave.
The signals of type III (model A3B3G5-D3M10;
Fig. 2, right panels) that are emitted by cores
collapsing very rapidly due to a very soft sub-nuclear EOS are
characterized by the lack of a strongly negative GW amplitude at bounce.
This results from the only modest rise of the rotational energy at
bounce implying a relatively small centrifugal contribution to the GW signal
![]() ,
and from the relatively
large positive contribution of the still collapsing layers outside to
the shock wave. Past bounce the signal exhibits rapid (on the
hydrodynamic time scale
,
and from the relatively
large positive contribution of the still collapsing layers outside to
the shock wave. Past bounce the signal exhibits rapid (on the
hydrodynamic time scale
![]() ms) oscillations
like the maximum density. The contributions from the outer layers of
the core are also responsible that the signal then remains positive for
an extended period of time (i.e. several oscillation periods) during
which the amplitude gradually decreases.
ms) oscillations
like the maximum density. The contributions from the outer layers of
the core are also responsible that the signal then remains positive for
an extended period of time (i.e. several oscillation periods) during
which the amplitude gradually decreases.
![\begin{figure}
\par\includegraphics[width=3.5cm,clip]{4306f03a.eps}\hspace*{2mm}...
...eps}\hspace*{2mm}
\includegraphics[width=3.5cm,clip]{4306f03d.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg182.gif) |
Figure 3:
The evolution of the magnetic energy parameters
|
| Open with DEXTER | |
The evolution of the magnetic energy is illustrated for four selected
models in Fig. 3 showing the ratio of the field energy and
the gravitational energy for the total (
![]() ),
toroidal (
),
toroidal (
![]() ), and poloidal (
), and poloidal (
![]() )
magnetic field, respectively. Both the total and the toroidal magnetic energies rise sharply at bounce
by a factor of 102 to 103. The magnetic energy is mostly
stored in form of the toroidal magnetic field
)
magnetic field, respectively. Both the total and the toroidal magnetic energies rise sharply at bounce
by a factor of 102 to 103. The magnetic energy is mostly
stored in form of the toroidal magnetic field ![]() ,
which is
created from the poloidal component by the action of differential
rotation. The amplification process extends beyond the end of our simulations.
,
which is
created from the poloidal component by the action of differential
rotation. The amplification process extends beyond the end of our simulations.
As our study is restricted to axisymmetric simulations, the main field
amplification mechanism is the conversion of rotational into magnetic
energy via the ![]() -dynamo. Axisymmetry suppresses most of the
instabilities of the (toroidal) field that are necessary to close the
dynamo loop of a full
-dynamo. Axisymmetry suppresses most of the
instabilities of the (toroidal) field that are necessary to close the
dynamo loop of a full
![]() dynamo, where a poloidal field is
converted into a toroidal one and amplified by differential rotation,
and then converted back into a poloidal field by some instability of the
toroidal field (Spruit 2002,1999).
dynamo, where a poloidal field is
converted into a toroidal one and amplified by differential rotation,
and then converted back into a poloidal field by some instability of the
toroidal field (Spruit 2002,1999).
Before we discuss the properties of some models in greater detail, we summarize a few general trends:
The field amplification via the ![]() -dynamo is most efficient, if
the poloidal field component is large compared to the toroidal one. A characteristic growth time for the generation of
-dynamo is most efficient, if
the poloidal field component is large compared to the toroidal one. A characteristic growth time for the generation of ![]() from a radial component
from a radial component
![]() is given by
(Meier et al. 1976)
is given by
(Meier et al. 1976)
The rate of field amplification is similar for the fast collapsing cores A1B3G5-D3M10, A2B4G5-D3M10 and A3B3G5-D3M10, which have a soft sub-nuclear EOS and which do not suffer a centrifugal bounce. A slightly more efficient amplification is observed for the initially more
differentially and faster rotating cores A2B4G5-D3M10 and A3B3G5-D3M10
than for the initially rigidly rotating model A1B3G5-D3M10. An even
faster amplification is observed for the slower collapsing model A1B3G3-D3M10, where 10 ms after bounce
![]()
![]() 10-5 compared to
10-5 compared to
![]()
![]() 10-6 for model A3B3G5-D3M10 (Fig. 3, upper two panels). This reflects
the different infall profiles of the cores whereby the regions of
strongest magnetic field (initially around and interior to the field
generating current loop at
10-6 for model A3B3G5-D3M10 (Fig. 3, upper two panels). This reflects
the different infall profiles of the cores whereby the regions of
strongest magnetic field (initially around and interior to the field
generating current loop at
![]() )
are
swept along to different positions in the core. In case of the model A1B3G3-D3M10 this region is much closer (
)
are
swept along to different positions in the core. In case of the model A1B3G3-D3M10 this region is much closer (
![]() )
to the center at the time of bounce than for model A3B3G5-D3M10, where it is located at
)
to the center at the time of bounce than for model A3B3G5-D3M10, where it is located at
![]() .
Therefore, the fraction of
the magnetic field that is available in the regions where the
.
Therefore, the fraction of
the magnetic field that is available in the regions where the
![]() -dynamo acts most efficiently is larger for the former model,
i.e. the field amplification can proceed more efficiently.
-dynamo acts most efficiently is larger for the former model,
i.e. the field amplification can proceed more efficiently.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4306f04a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg197.gif) |
Figure 4:
Magnetic pressure (color shaded), velocity field (arrows), and
magnetic field lines of model A1B3G3-D3M10 at
|
| Open with DEXTER | |
During collapse and to an even larger extent during and after core bounce the magnetic field configuration of model A1B3G3-D3M10 is considerably distorted. The field lines initially surrounding the off-center current loop (Fig. 1) are pulled towards the center. Apart from an overall compression the field geometry remains basically the same as in the initial model. A complex pattern of "filamentary'' regions of high and low magnetic fields develops as the field lines get entangled by the fluid flow around and after bounce. No simple classification of the magnetic field as a dipole, quadrupole, etc., is possible. In the subsequent evolution the tangled fields follow the outward propagating shock front which is almost spherically symmetric in this initially rigidly rotating model (Fig. 4).
Multiple-bounce models that experience several phases of collapse and
expansion exhibit a similar evolution of the magnetic field. During a contraction phase angular momentum conservation yields a more efficient amplification of the magnetic field energy, whereas
![]() grows much slower in an expansion phase. This is
the case for model A2B4G1-D3M10 (Fig. 3, lower left
panel). The magnetic energy parameter
grows much slower in an expansion phase. This is
the case for model A2B4G1-D3M10 (Fig. 3, lower left
panel). The magnetic energy parameter
![]() rises by a factor
rises by a factor ![]() 3 during 10 ms around core bounce (
3 during 10 ms around core bounce (
![]() ), but then requires 40 ms to amplify the field by another factor of
), but then requires 40 ms to amplify the field by another factor of ![]() 1.6. The amplification rate
increases again strongly during the subsequent contraction phase. For
model A4B5G5-D3M10, the amplification factor during core bounce is about 20, but later the field energy gets greatly reduced (
1.6. The amplification rate
increases again strongly during the subsequent contraction phase. For
model A4B5G5-D3M10, the amplification factor during core bounce is about 20, but later the field energy gets greatly reduced (
![]() drops by a factor
drops by a factor ![]() 3.5) during the
extremely violent expansion that follows the bounce in this model
(Fig. 3, lower right panel; the evolution of the maximum
density is shown in Fig. 19). Afterwards, differential
rotation again starts to increase the magnetic field, but on a longer
time scale.
3.5) during the
extremely violent expansion that follows the bounce in this model
(Fig. 3, lower right panel; the evolution of the maximum
density is shown in Fig. 19). Afterwards, differential
rotation again starts to increase the magnetic field, but on a longer
time scale.
Model A4B5G5-D3M10 possesses a torus shaped initial density
distribution, and maintains it throughout the entire evolution. The
field structure of this model tends to become very complex during the
evolution. In the final model, at
![]() ,
the field
exhibits both sheet-like regions of strong fields (
,
the field
exhibits both sheet-like regions of strong fields (![]()
![]() off the axis), and also toroidal (at
off the axis), and also toroidal (at
![]() ,
,
![]() )
and cylindrical (e.g.
)
and cylindrical (e.g. ![]()
![]() off the axis) weak-field regions
(Fig. 5).
off the axis) weak-field regions
(Fig. 5).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4306f05a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg203.gif) |
Figure 5:
Same as Fig. 5, but for model A4B5G5-D3M10 at
|
| Open with DEXTER | |
For initially strong magnetic fields the collapse shows significant
deviations from the purely hydrodynamic case. The most striking new
feature is the braking of the rotation of the core by magnetic stresses.
The initially strongest fields are amplified by differential rotation
during collapse to such a level that they can cause considerable
braking, whereas initial fields of the order of
![]() or less require the action of an MRI-like instability to reach a level
sufficient for significant angular momentum transport on the collapse
time scale. In the following we will first discuss the former class of
models divided into models bouncing due to pressure forces
(Sect. 4.2.1) or centrifugal forces
(Sect. 4.2.2), and later address the issue of the MRI in
Sect. 4.3.
or less require the action of an MRI-like instability to reach a level
sufficient for significant angular momentum transport on the collapse
time scale. In the following we will first discuss the former class of
models divided into models bouncing due to pressure forces
(Sect. 4.2.1) or centrifugal forces
(Sect. 4.2.2), and later address the issue of the MRI in
Sect. 4.3.
![\begin{figure}
\par\mbox{\includegraphics[width=5.45cm,clip]{4306f06a.eps} \incl...
...{4306f06e.eps} \includegraphics[width=5.45cm,clip]{4306f06f.eps} }
\end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg204.gif) |
Figure 6:
The dynamics and the GW signal of model A1B3G3-D3M12.
The upper left and middle panels provide a comparison of the
evolution of the rotational energy parameter
|
| Open with DEXTER | |
As in the case of weak-field models, the poloidal field energy of a single bounce models such as A1B3G3-D3M12 is approximately constant during the early post-bounce evolution, but it is strongly amplified afterwards by MRI-like modes in the core which efficiently remove angular momentum from the inner core and decrease its rotational energy. The evolution of the rotational energy hence shows a clear deviation from that of a weak-field model (Fig. 6), which however should not be the case, as the MRI does not depend on the seed field. We will explain in Sect. 4.3 why this different behavior arises.
The loss of rotational support also affects the density structure. The
core of model A1B3G3-D3M12 is slightly less rotationally flattened than
the core of a non-magnetized model such as A1B3G3-D3M10. The shock
that forms at bounce, when the models hardly differ, is unaffected by
the different evolution of the central region, whereas matter in the
central region experiences an additional acceleration due to the
presence of the strong magnetic field. The decrease of the rotation
rate, and also of the degree of differential rotation in the
strong-field case limits the amplification of the toroidal field
component by wrapping of field lines (Fig. 6, upper
right panel), and the total magnetic energy has a significant poloidal
contribution. At
![]() ,
the ratio of toroidal and
total magnetic energy has dropped to a value of about
,
the ratio of toroidal and
total magnetic energy has dropped to a value of about ![]() .
The
poloidal component grows a little during the post-bounce evolution by
the action of meridional motions in the core. When the magnetic field
becomes dynamically important, magnetic energy is used to accelerate the
fluid, which puts an end to the phase of efficient field amplification.
During the late stages of evolution, the total field energy remains
approximately constant. Its final value corresponds to
.
The
poloidal component grows a little during the post-bounce evolution by
the action of meridional motions in the core. When the magnetic field
becomes dynamically important, magnetic energy is used to accelerate the
fluid, which puts an end to the phase of efficient field amplification.
During the late stages of evolution, the total field energy remains
approximately constant. Its final value corresponds to
![]() .
The field structure of model A1B3G3-D3M12 differs from that of the weak-field core A1B3G3-D3M10 in the central parts of the core at late times due to the MRI modes (that could not be resolved for the weaker field; see Sect. 4.3),
but farther away from the center the fields have a similar topology.
.
The field structure of model A1B3G3-D3M12 differs from that of the weak-field core A1B3G3-D3M10 in the central parts of the core at late times due to the MRI modes (that could not be resolved for the weaker field; see Sect. 4.3),
but farther away from the center the fields have a similar topology.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4306f07a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg209.gif) |
Figure 7:
Snapshot of the inner regions of model A1B3G3-D3M12 at
|
| Open with DEXTER | |
Around the time of bounce the GW signal of model A1B3G3-D3M12 is very
similar to the one of the less magnetized core A1B3G3-D3M10, and also
the contributions of the individual parts of the total signal are
comparable (Fig. 6, lower panels). In the
post-bounce evolution, both the hydrodynamic and the gravitational part
of the amplitude start to decrease in magnitude, as the rotationally
induced asphericity of the core decreases along with the extraction of
rotational energy. The magnetic amplitude increases strongly as
magnetic forces act on the core decreasing its rotation. The
oscillations of the core are still imprinted on the post-bounce GW amplitude, but their impact on the signal decreases with time. In the
long run, the amplitude assumes positive values and varies relatively
little. Dynamically, this phase is characterized by the emergence of a weak outflow along the polar axis far behind the shock wave created at
core bounce. This outflow is predominantly driven by magnetic forces
(Fig. 7). The positive long-term GW amplitude
is mainly due to the
![]() term which is large
inside the outflow, whereas the inner parts of the model and the almost
spherical shock wave contribute little to the total signal. Despite the
differences in the post-bounce GW amplitude contributions of the two models A1B3G3-D3M10 and A1B3G3-D3M12 their total signals are quite similar, i.e. distinguishing the two models observationally would be very difficult.
term which is large
inside the outflow, whereas the inner parts of the model and the almost
spherical shock wave contribute little to the total signal. Despite the
differences in the post-bounce GW amplitude contributions of the two models A1B3G3-D3M10 and A1B3G3-D3M12 their total signals are quite similar, i.e. distinguishing the two models observationally would be very difficult.
![\begin{figure}
\par\mbox{\includegraphics[width=5.45cm,clip]{4306f08a.eps} \incl...
...{4306f08e.eps} \includegraphics[width=5.45cm,clip]{4306f08f.eps} }
\end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg211.gif) |
Figure 8:
The dynamical evolution and the GW signal of model A1B3G3-D3M13.
The upper panels display the temporal evolution of the rotational
energy parameter
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4306f09a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg213.gif) |
Figure 9:
Snapshot of model A1B3G3-D3M13 at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4306f10a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg215.gif) |
Figure 10:
Same as Fig. 9, but at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4306f11a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg217.gif) |
Figure 11:
Same as Fig. 9, but at
|
| Open with DEXTER | |
Similar features as those observed in the case of model A1B3G3-D3M12
(Fig. 6) are present in the evolution of the
stronger magnetized model A1B3G3-D3M13 (Fig. 8),
but they are much more prominent. Unlike all previously discussed
models, this core shows significant deviations from the purely
hydrodynamic case already during collapse. For model A1B3G3-D3M13 the
core bounce is delayed by ![]()
![]() compared to the
weaker magnetized models A1B3G3-D3M10...12. The rotational energy
reaches a maximum value of
compared to the
weaker magnetized models A1B3G3-D3M10...12. The rotational energy
reaches a maximum value of
![]() near bounce, which is lower than in the less magnetized models
(
near bounce, which is lower than in the less magnetized models
(
![]() ). Within the next
). Within the next
![]()
![]() the core looses
the core looses ![]()
![]() of the
rotational energy it had acquired at bounce. Subsequently, the rate of
energy loss decreases, and the core contracts
(Fig. 8). Its maximum density rises from
of the
rotational energy it had acquired at bounce. Subsequently, the rate of
energy loss decreases, and the core contracts
(Fig. 8). Its maximum density rises from
![]()
![]()
![]() in the
first post-bounce density minimum to
in the
first post-bounce density minimum to
![]()
![]()
![]() at
at
![]() before it starts to decreases by a small amount again. The process of magnetic
braking prevents a further amplification of the field, and it prevents
the transformation of poloidal into toroidal magnetic field. The ratio
before it starts to decreases by a small amount again. The process of magnetic
braking prevents a further amplification of the field, and it prevents
the transformation of poloidal into toroidal magnetic field. The ratio
![]() does not approach unity, as in case of the models with weaker initial fields, but it remains below
does not approach unity, as in case of the models with weaker initial fields, but it remains below ![]()
![]() decreasing slowly later. At
decreasing slowly later. At
![]() ,
when we stopped the computations, the value of
,
when we stopped the computations, the value of
![]() had dropped to
had dropped to
![]() ,
and we expect it to eventually decrease to a value of
,
and we expect it to eventually decrease to a value of ![]()
![]() .
.
In model A1B3G3-D3M12 the immediate post-bounce core is very similar to
the corresponding non-magnetic one as the magnetic field is not
sufficiently strong to change the dynamics unless an MRI-like
instability sets in. This is different from the more strongly
magnetized model A1B3G3-D3M13, where without the MRI the combined
amplification due to contraction and differential rotation is sufficient
to cause the braking effect. This is generally true for all of our
models: very strong initial fields (>
![]() )
do not
need amplification by an instability to brake the core, whereas weaker
ones heavily depend on it.
)
do not
need amplification by an instability to brake the core, whereas weaker
ones heavily depend on it.
After bounce, the shock wave develops a non-spherical, bulb-like shape, and the twisted field lines give rise to a highly magnetized post-shock fluid that pushes the shock near the equatorial plane around
![]() (Fig. 9). Near the
axis, the immediate post-shock matter is only weakly magnetized, the
ratio of gas pressure and magnetic pressure being largest at a significantly smaller radius (
(Fig. 9). Near the
axis, the immediate post-shock matter is only weakly magnetized, the
ratio of gas pressure and magnetic pressure being largest at a significantly smaller radius (
![]() )
than the shock position (
)
than the shock position (
![]() ). The shock maintains its bulb-like shape also during the secondary contraction phase that goes along with the extraction of rotational energy, and fast outflow both at high and low latitudes. At later times (
). The shock maintains its bulb-like shape also during the secondary contraction phase that goes along with the extraction of rotational energy, and fast outflow both at high and low latitudes. At later times (
![]() ,
Fig. 10), the
fluid pattern has changed. The formerly important outflow near the
equator stalls, and the shock surface becomes more elongated. The
near-axis outflow velocity has further increased, its maximum value
being
,
Fig. 10), the
fluid pattern has changed. The formerly important outflow near the
equator stalls, and the shock surface becomes more elongated. The
near-axis outflow velocity has further increased, its maximum value
being
![]() in the strongly magnetized region
well behind the shock (
in the strongly magnetized region
well behind the shock (
![]() ). In the outflow along the
rotational axis, a cylindrical shell of very low pressure gas can be
identified (at
). In the outflow along the
rotational axis, a cylindrical shell of very low pressure gas can be
identified (at
![]() in
Fig. 10). The structure of the magnetic field is
dominated by two extended highly magnetized regions, one located near
the equator at
in
Fig. 10). The structure of the magnetic field is
dominated by two extended highly magnetized regions, one located near
the equator at
![]() ,
,
![]() ), and a cylindrical one oriented along the rotational axis
having a width of
), and a cylindrical one oriented along the rotational axis
having a width of ![]() 100 km (left panel of
Fig. 10). At an even later epoch,
100 km (left panel of
Fig. 10). At an even later epoch,
![]() (Fig. 11), only little has changed
near the equatorial plane, however at the axis the highly magnetic gas
is about to catch up with the shock wave, which is now significantly
prolate with an axis ratio of about 3:2. The outflow has accelerated
further (vr = 8
(Fig. 11), only little has changed
near the equatorial plane, however at the axis the highly magnetic gas
is about to catch up with the shock wave, which is now significantly
prolate with an axis ratio of about 3:2. The outflow has accelerated
further (vr = 8 ![]()
![]() ), the
maximum velocity corresponding to the highly magnetized regions behind
the shock at
), the
maximum velocity corresponding to the highly magnetized regions behind
the shock at
![]() .
Hence, we see the formation of a jet-like outflow from the core.
.
Hence, we see the formation of a jet-like outflow from the core.
In its very interior the core is rotating slower than its non-magnetic
variant at late times. Furthermore, it has developed a roughly toroidal
region of relatively slow and highly rigid counter-rotation. This
region grows from a layer at
![]() ,
i.e. near the
edge of the inner core, which experiences sufficiently strong magnetic
stresses to reverse its direction of rotation. Interior to the
retrograde rotating region the angular velocity decreases with time.
,
i.e. near the
edge of the inner core, which experiences sufficiently strong magnetic
stresses to reverse its direction of rotation. Interior to the
retrograde rotating region the angular velocity decreases with time.
Assuming that the total energy density of a fluid element,
![]() ,
is converted entirely into kinetic energy
,
is converted entirely into kinetic energy
![]() ,
terminal outflow velocities
,
terminal outflow velocities
![]() of up to 1.85
of up to 1.85 ![]()
![]() are observed for
model A1B3G3-D3M13 at late times, particularly in the bipolar outflow
along the rotation axis (Fig. 11). The large
velocities stretch our non-relativistic MHD approach, and imply
that a realistic simulation of the late evolution of the outflow will
require relativistic MHD.
are observed for
model A1B3G3-D3M13 at late times, particularly in the bipolar outflow
along the rotation axis (Fig. 11). The large
velocities stretch our non-relativistic MHD approach, and imply
that a realistic simulation of the late evolution of the outflow will
require relativistic MHD.
The GW amplitude of model A1B3G3-D3M13 (Fig. 8,
lower panels) is enhanced by about ![]() at core bounce. After
bounce, ringing on the dynamical time scale of the core the average
amplitude shifts to positive values. The amplitudes and frequencies
of the oscillations are hardly affected by the overall shift of the
average amplitude to positive values implying a different origin of
the oscillations and the overall shift. A few milliseconds after
bounce
at core bounce. After
bounce, ringing on the dynamical time scale of the core the average
amplitude shifts to positive values. The amplitudes and frequencies
of the oscillations are hardly affected by the overall shift of the
average amplitude to positive values implying a different origin of
the oscillations and the overall shift. A few milliseconds after
bounce
![]() grows to
grows to ![]()
![]() ,
and the rapid
variations of the signal cease. The hydrodynamic and gravitational
contributions to the total amplitude are greatly reduced in magnitude.
The inner core has lost a large amount of its rotational energy and is
of almost spherical shape. Its contribution to the total signal
amplitude is hence relatively small for epochs well after bounce.
,
and the rapid
variations of the signal cease. The hydrodynamic and gravitational
contributions to the total amplitude are greatly reduced in magnitude.
The inner core has lost a large amount of its rotational energy and is
of almost spherical shape. Its contribution to the total signal
amplitude is hence relatively small for epochs well after bounce.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4306f12a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg247.gif) |
Figure 12:
The hydrodynamic plus gravitational parts of the GW amplitude of
model A1B3G3-D3M13 at
|
| Open with DEXTER | |
While the hydrodynamic amplitude produced by the innermost layers of the core is very small, the gravitational and magnetic contributions reach quite large values of several 102 cm. However, as both contributions are of opposite sign they cancel each other almost completely (Fig. 8), i.e. only a small net amplitude results. The relative smallness of the hydrodynamic amplitude of the central core indicates that - once most of the rotational energy is extracted - magnetic forces may become more important for the core's structure than the centrifugal ones.
The very non-spherical shape of the shock wave, and in particular the
appearance of the jet-like outflow that carries a large (radial)
kinetic energy, causes a long-lasting positive GW amplitude the major
contribution being the
![]() amplitude of the
outflow (Fig. 12). Growing larger with time this
contribution eventually makes the hydrodynamic amplitude to become
positive at
amplitude of the
outflow (Fig. 12). Growing larger with time this
contribution eventually makes the hydrodynamic amplitude to become
positive at
![]() .
Thus, a bipolar motion can be
identified in the GW signature through the appearance of a long-lasting
positive signal.
.
Thus, a bipolar motion can be
identified in the GW signature through the appearance of a long-lasting
positive signal.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{4306f13a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg250.gif) |
Figure 13:
Snapshot of model A3B3G5-D3M13 at
|
| Open with DEXTER | |
The behavior just described holds for models A1B3G3/5-D3Mm, A2B4G5-D3Mm,
and A3B3G5-D3Mm, too. They differ, however, concerning the time scales
and the vigorousness of the phenomena. Most dramatic is the evolution
of model A3B3G5-D3M13 (Fig. 8), where the loss of
rotational energy allows the core to contract to densities
(
![]()
![]()
![]() )
that
exceed the bounce density
)
that
exceed the bounce density
![]()
![]()
![]() by up to
by up to ![]() .
The shock wave is already strongly prolate when it forms, and the magnetic field is highly concentrated both towards the equator and - like in model A1B3G3-D3M13 - in a cylindrical region oriented along the rotation axis. The rapidly moving, highly magnetized outflow deforms the shock wave giving rise to a shock surface with an axis ratio of about 3:1. At
.
The shock wave is already strongly prolate when it forms, and the magnetic field is highly concentrated both towards the equator and - like in model A1B3G3-D3M13 - in a cylindrical region oriented along the rotation axis. The rapidly moving, highly magnetized outflow deforms the shock wave giving rise to a shock surface with an axis ratio of about 3:1. At
![]() ,
magnetic (hoop) stresses in the pinched toroidal field
have accelerated the gas further yielding a so-called "nose cone''
(well known from simulations of magnetized jets) that is visible in the
outermost part of the jet-like outflow (Fig. 13).
,
magnetic (hoop) stresses in the pinched toroidal field
have accelerated the gas further yielding a so-called "nose cone''
(well known from simulations of magnetized jets) that is visible in the
outermost part of the jet-like outflow (Fig. 13).
The GW amplitude of model A3B3G5-D3M13 (Fig. 14), whose weak-field counterpart A3B3G5-D3M10 emits a GW signal of type III (Fig. 2), is modified by the strong initial field. Relative to the weak-field model, the pre-bounce maximum is enhanced, and the size of the (negative) peak at bounce is reduced by the same amount, whereas the amplitude of the first (positive) post-bounce peak remains nearly unchanged. As the core loses angular momentum, the size of the hydrodynamic and gravitational contributions to the GW amplitude decreases. The post-bounce oscillations of the signal, which are mainly due to the central core, are superimposed on a nearly constant positive amplitude of half the size of the bounce amplitude indicating the presence of the collimated bipolar outflow (Fig. 13). The evolution of the magnetic contributions of models A1B3G3-D3M13 and A3B3G5-D3M13 are similar. In both models, a phase of positive amplitude concurrent with the most efficient braking of the core's rotation is followed by a decrease to large negative values (Fig. 14, lower right panel). In the latter phase the magnetic amplitude, which is mostly produced in the central core, provides the main contribution to the total signal.
Increasing the initial magnetic field strength to ![]()
![]() in models which exhibit a type-I GW signal in the non-magnetic case, the size of the large (negative) bounce amplitude
decreases slightly. This also holds for even stronger magnetic fields in
case of models that are influenced by rotation to a higher degree such
as A3B2G4-D3Mm and A3B3G4-D3Mm, respectively. However, for rigidly and
moderately fast rotating models (A1B1G3-D3Mm and A1B3G3-D3Mm) the size
of the bounce signal grows again strongly when the initial field
strength reaches
in models which exhibit a type-I GW signal in the non-magnetic case, the size of the large (negative) bounce amplitude
decreases slightly. This also holds for even stronger magnetic fields in
case of models that are influenced by rotation to a higher degree such
as A3B2G4-D3Mm and A3B3G4-D3Mm, respectively. However, for rigidly and
moderately fast rotating models (A1B1G3-D3Mm and A1B3G3-D3Mm) the size
of the bounce signal grows again strongly when the initial field
strength reaches
![]() .
.
The ratio of the GW amplitudes of the positive peaks immediately prior to and immediately after the signal minimum at bounce can both increase and decrease by the effects of a strong magnetic field. In type-I models with a small influence of the rotation on the dynamics, a stronger initial field increases the ratio, and for sufficiently fast rotating models (A3B2G4-D3Mm) it decreases. Two models with a type-I GW signal are close to the transition from a bounce caused by pressure or centrifugal forces (A2B4G4-DdMm and A3B3G4-DdMm), i.e. their cores are only partially stabilized by the stiffening of the EOS at nuclear matter density. For both models the amplitude ratio of the pre- and post-bounce peaks increases with increasing magnetic field strength, while it decreases for most type-III models.
![\begin{figure}
\par\mbox{\includegraphics[width=5.6cm,clip]{4306f14a.eps} \inclu...
...]{4306f14e.eps} \includegraphics[width=5.6cm,clip]{4306f14f.eps} }
\end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg254.gif) |
Figure 14:
The dynamical evolution and the GW signal of model A3B3G5-D3M13.
The upper panels display the temporal evolution of the rotational
energy parameter
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.6cm,clip]{4306f15a.eps} \inclu...
...]{4306f15e.eps} \includegraphics[width=5.6cm,clip]{4306f15f.eps} }
\end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg255.gif) |
Figure 15:
The evolution of the rotational energy parameter
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.6cm,clip]{4306f16a.eps} \inclu...
...{4306f16e.eps} \includegraphics[width=5.6cm,clip]{4306f16f.eps} }
\end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg256.gif) |
Figure 16:
The dynamical evolution and the GW signal of model A3B3G3-D3M13.
The upper panels display the temporal evolution of the rotational
energy parameter
|
| Open with DEXTER | |
The weak-field models of series A3B3G3-D3Mm belong to the transition class between standard-type and centrifugally bouncing cores. They bounce mostly due to centrifugal forces and exhibit large-scale pulsations after bounce, but their maximum density exceeds nuclear matter density during bounce. Both the period and the damping of the pulsations are significantly larger than for purely centrifugally bouncing type-II models (Fig. 15). Their GW signal consists of a pronounced peak of negative amplitude at bounce, and subsequent relatively long-period oscillations.
For the strong-field variants of this model series, e.g. model A3B3G3-D3M12 (Fig. 15), the main evolutionary effect
of the magnetic field is the extraction of rotational energy after
bounce that proceeds on time scales much longer than the dynamic time
scale of the inner core. Model A3B3G3-D3M12 reaches a maximum rotation
parameter
![]() at bounce, which is nearly
the same value as in the non-magnetic case. At the time of the second
density maximum
at bounce, which is nearly
the same value as in the non-magnetic case. At the time of the second
density maximum
![]() is only slightly smaller than in the
weak-field model A3B3G3-D3M10, but at the next (3rd) maximum the
rotational energy has decreased by about
is only slightly smaller than in the
weak-field model A3B3G3-D3M10, but at the next (3rd) maximum the
rotational energy has decreased by about ![]() .
Unlike in the
weak-field model no fourth density maximum occurs. Instead,
.
Unlike in the
weak-field model no fourth density maximum occurs. Instead,
![]() decreases monotonically. The rotation rate of model A3B3G3-D3M12 is sufficiently large for a sufficiently long time to allow the core to exhibit several centrifugal pulsations before it settles down in a pressure supported final equilibrium state. During these
pulsations the time-averaged value of
decreases monotonically. The rotation rate of model A3B3G3-D3M12 is sufficiently large for a sufficiently long time to allow the core to exhibit several centrifugal pulsations before it settles down in a pressure supported final equilibrium state. During these
pulsations the time-averaged value of
![]() increases,
and densities significantly larger than the bounce density
increases,
and densities significantly larger than the bounce density
![]()
![]()
![]() are reached.
are reached.
The GW signal of the strong-field model A3B3G3-D3M12 is similar to that
of the weak-field model A3B3G3-D3M10 during the first ![]()
![]() after bounce when the cores of both models still undergo large-scale pulsations. Later when the rotational energy has decreased sufficiently and the pulsations begin to fade away, the signals begin to
differ slightly. The maximum density now increases monotonically.
Rotation is no longer important for the core's stabilization, as it is
supported by pressure forces. Thus, like in the case of a standard-type core (e.g. A1B3G3-DdMm), the rapid oscillations of the GW amplitude for
after bounce when the cores of both models still undergo large-scale pulsations. Later when the rotational energy has decreased sufficiently and the pulsations begin to fade away, the signals begin to
differ slightly. The maximum density now increases monotonically.
Rotation is no longer important for the core's stabilization, as it is
supported by pressure forces. Thus, like in the case of a standard-type core (e.g. A1B3G3-DdMm), the rapid oscillations of the GW amplitude for
![]() occur on the core's
dynamic time scale. Superimposed to the oscillations is a positive mean
amplitude
occur on the core's
dynamic time scale. Superimposed to the oscillations is a positive mean
amplitude
![]() ,
which results
from the enhanced asphericity of the shock wave as compared to that of
the weak-field model.
,
which results
from the enhanced asphericity of the shock wave as compared to that of
the weak-field model.
The most strongly magnetized model of series A3B3G3-D3Mm, namely model A3B3G3-D3M13, behaves very differently from its weak-field variants as e.g. model A3B3G3-D3M10 (Fig. 15). Unlike the latter model it suffers a single bounce at
![]()
![]()
![]() (a value about
(a value about ![]() larger than for the weak-field models) with a subsequent contraction phase caused by the decrease of the core's rotational energy. After bounce the maximum
density reaches a value of
larger than for the weak-field models) with a subsequent contraction phase caused by the decrease of the core's rotational energy. After bounce the maximum
density reaches a value of
![]()
![]()
![]() .
Unlike model A3B3G3-D3M12, it does not exhibit any large-scale pulsations. Instead, it rapidly approaches a high density state without an intermediate phase where the density in the
entire core is less that nuclear matter density, as it is the case for
model A3B3G3-D3M12. The rotational energy (
.
Unlike model A3B3G3-D3M12, it does not exhibit any large-scale pulsations. Instead, it rapidly approaches a high density state without an intermediate phase where the density in the
entire core is less that nuclear matter density, as it is the case for
model A3B3G3-D3M12. The rotational energy (
![]() )
is less than for models with weaker initial fields
(e.g.
)
is less than for models with weaker initial fields
(e.g.
![]() for model A3B3G3-D3M10), and
decreases by
for model A3B3G3-D3M10), and
decreases by ![]() within 15 ms (Fig. 16).
within 15 ms (Fig. 16).
The collapse and post-bounce dynamics of model A3B3G3-D3M13 is similar
to that of strong-field single-bounce models, as e.g. model A1B3G3-D3M13. Many features of the latter model are also present in model A3B3G3-D3M13: the bulb-like shock surface, the two highly
magnetized post-shock regions (one near the equator and the other one
along the polar axis), and a region of retrograde rotation near the
equatorial plane at the edge of the inner core. The ratio of magnetic
and gas pressure is largest at the axis at
![]() well behind the shock located at
well behind the shock located at
![]() .
.
The GW signal of model A3B3G3-D3M13 is qualitatively similar to that of
its less strongly magnetized variant A3B3G3-D3M12, but the features
caused by the magnetic field are more pronounced
(Fig. 16). The peak amplitude at bounce
![]() is, contrary to model A3B3G3-D3M12, considerably less negative than in the weak-field model A3B3G3-D3M10 (
is, contrary to model A3B3G3-D3M12, considerably less negative than in the weak-field model A3B3G3-D3M10 (
![]() ).
Immediately after bounce the GW signal shows certain similarities with
that of model A1B3G3-D3M13 (Fig. 8): a large
positive peak is followed by a series of oscillations occurring on the
local dynamic time scale superimposed on an increase of the mean
amplitude to a value of
).
Immediately after bounce the GW signal shows certain similarities with
that of model A1B3G3-D3M13 (Fig. 8): a large
positive peak is followed by a series of oscillations occurring on the
local dynamic time scale superimposed on an increase of the mean
amplitude to a value of
![]() within
within
![]() ,
which is the time it takes to turn
the initially roughly spherical shock into a relatively wide bipolar
outflow directed along the rotation axis.
,
which is the time it takes to turn
the initially roughly spherical shock into a relatively wide bipolar
outflow directed along the rotation axis.
Similar to cores bouncing due to pressure forces, the extraction of
rotational energy from cores bouncing due to centrifugal forces proceeds
qualitatively differently for models with an initial magnetic field
strength of
![]() and
and
![]() ,
respectively. For the weaker field the extraction process relies on an instability-driven angular momentum transport, which is not required
for the stronger field models.
,
respectively. For the weaker field the extraction process relies on an instability-driven angular momentum transport, which is not required
for the stronger field models.
![\begin{figure}
\par\mbox{\includegraphics[width=5.4cm,clip]{4306f17a.eps} \inclu...
...]{4306f17e.eps} \includegraphics[width=5.4cm,clip]{4306f17f.eps} }
\end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg274.gif) |
Figure 17:
The dynamical evolution and the GW signal of model A2B4G1-D3M13.
The upper panels display the temporal evolution of the rotational
energy parameter
|
| Open with DEXTER | |
Unlike the other models, which collapse to higher densities when angular
momentum transport by the magnetic field becomes dynamically important,
model A2B4G1-D3M13 bounces at a lower density (
![]()
![]()
![]() compared to
compared to
![]()
![]()
![]() in the weak-field case).
At bounce its rotational energy (
in the weak-field case).
At bounce its rotational energy (
![]() )
is less
than that of model A2B4G1-D3M11 (
)
is less
than that of model A2B4G1-D3M11 (
![]() ), which
has an initially 100 times weaker magnetic field. After bounce the
rotational energy continues to decrease, and the core eventually suffers
a second collapse that is stopped at
), which
has an initially 100 times weaker magnetic field. After bounce the
rotational energy continues to decrease, and the core eventually suffers
a second collapse that is stopped at
![]()
![]()
![]() (Fig. 17). During
the second collapse
(Fig. 17). During
the second collapse
![]() rises temporarily slightly
again, but angular momentum redistribution prevents the shock formed by
centrifugal forces (at a similar density as the one resulting from the
first bounce) from stopping the infall. Thus, a large fraction of the
inner core continues to fall towards the center, until the collapse is
halted by the stiffening of the equation of state, i.e. by a bounce due
to pressure forces. A shock forms at the edge of the still very
extended inner core (
rises temporarily slightly
again, but angular momentum redistribution prevents the shock formed by
centrifugal forces (at a similar density as the one resulting from the
first bounce) from stopping the infall. Thus, a large fraction of the
inner core continues to fall towards the center, until the collapse is
halted by the stiffening of the equation of state, i.e. by a bounce due
to pressure forces. A shock forms at the edge of the still very
extended inner core (
![]() compared to
compared to
![]() in the previously discussed
models) at
in the previously discussed
models) at
![]() at the beginning of the "plateau'' in
the evolution of
at the beginning of the "plateau'' in
the evolution of
![]() (see upper middle panel of
Fig. 17), and it becomes slightly prolate. About 15 ms later (
(see upper middle panel of
Fig. 17), and it becomes slightly prolate. About 15 ms later (
![]() )
this shock has reached a radius of
)
this shock has reached a radius of
![]() (Fig. 18). The magnetic field of model A2B4G1-D3M13 is less amplified and deformed than in the deeper collapsing single-bounce models such as e.g. model A1B3G3-D3M13. The
largest magnetic to gas pressure ratios are reached well behind the
shock at about
(Fig. 18). The magnetic field of model A2B4G1-D3M13 is less amplified and deformed than in the deeper collapsing single-bounce models such as e.g. model A1B3G3-D3M13. The
largest magnetic to gas pressure ratios are reached well behind the
shock at about
![]() .
.
The GW signal does not resemble any of the types used to classify
non-magnetic models. Hence, we suggest to introduce a new type-IV GW signal (Fig. 17) which it is weaker at bounce
(
![]() )
than in the non-magnetic
case (
)
than in the non-magnetic
case (
![]() ), but the amplitude
remains large for a longer time period due to the longer phase of
maximum contraction. Until the second collapse the signal varies on
time scales (
), but the amplitude
remains large for a longer time period due to the longer phase of
maximum contraction. Until the second collapse the signal varies on
time scales (
![]() )
that are short compared
to the pulsation periods of the non-magnetic case, but comparable to
the sound crossing time of the relatively extended inner core. After
)
that are short compared
to the pulsation periods of the non-magnetic case, but comparable to
the sound crossing time of the relatively extended inner core. After
![]() the oscillation frequency and the amplitude
of the GW signal strongly increases as the second collapse begins.
During the entire post-bounce evolution the large negative
gravitational and hydrodynamic (dominated by the centrifugal amplitude)
contributions to the GW signal, and the large positive magnetic
contribution add up to a total GW amplitude which is very small compared
to the individual contributions.
the oscillation frequency and the amplitude
of the GW signal strongly increases as the second collapse begins.
During the entire post-bounce evolution the large negative
gravitational and hydrodynamic (dominated by the centrifugal amplitude)
contributions to the GW signal, and the large positive magnetic
contribution add up to a total GW amplitude which is very small compared
to the individual contributions.
Model A4B5G5-D3M13 bounces at a slightly higher maximum density
(
![]()
![]()
![]() )
than its
weak-field variant A4B5G5-D3M10 (
)
than its
weak-field variant A4B5G5-D3M10 (
![]()
![]()
![]() ;
Fig. 19). The maximum rotational energy at bounce is barely affected by the presence of the strong magnetic field, but it changes the density structure of the core
completely in the subsequent evolution. Models A4B5G5-D3Mm (
;
Fig. 19). The maximum rotational energy at bounce is barely affected by the presence of the strong magnetic field, but it changes the density structure of the core
completely in the subsequent evolution. Models A4B5G5-D3Mm (![]() )
maintain a toroidal density structure (
)
maintain a toroidal density structure (
![]() )
during their entire evolution
(Sect. 4.1), but in model A4B5G5-D3M13 the
density structure is changed by magnetic forces. Up to a few milliseconds after bounce (
)
during their entire evolution
(Sect. 4.1), but in model A4B5G5-D3M13 the
density structure is changed by magnetic forces. Up to a few milliseconds after bounce (
![]() ), the core of model A4B5G5-D3M13 evolves only marginally differently than its
weak-field variants. Later, however, magnetic stresses transfer
angular momentum from the still toroidal density distribution into the
surrounding gas, whereby the torus transforms into a flattened
configuration, which has its density maximum only slightly off-center
(Fig. 20). During this phase, the core develops a retrograde rotating region near the equatorial plane. The core's transformation process is associated with a large increase of its maximum density comparable with that occurring during the first collapse
(Fig. 19).
), the core of model A4B5G5-D3M13 evolves only marginally differently than its
weak-field variants. Later, however, magnetic stresses transfer
angular momentum from the still toroidal density distribution into the
surrounding gas, whereby the torus transforms into a flattened
configuration, which has its density maximum only slightly off-center
(Fig. 20). During this phase, the core develops a retrograde rotating region near the equatorial plane. The core's transformation process is associated with a large increase of its maximum density comparable with that occurring during the first collapse
(Fig. 19).
During the second collapse, both the magnetic and the rotational energy
of the core increase. The magnetic energy (
![]() )
exceeds that of the primary collapse (
)
exceeds that of the primary collapse (
![]() ), and the rotational energy exceeds slightly the limit for the
dynamic instability of MacLaurin ellipsoids (
), and the rotational energy exceeds slightly the limit for the
dynamic instability of MacLaurin ellipsoids (
![]() ), but only for about 1 ms. We note that the rotational
energy reaches its maximum value well before the density does, which is
different from all other models. Later on, the rotation parameter
rapidly decreases well below the corresponding value of the
non-magnetic case.
), but only for about 1 ms. We note that the rotational
energy reaches its maximum value well before the density does, which is
different from all other models. Later on, the rotation parameter
rapidly decreases well below the corresponding value of the
non-magnetic case.
The shock has a very prolate shape at core bounce, its axis ratio being
![]() 2:1. At large latitudes, the ratio of magnetic and gas
pressure is largest well behind the shock (
2:1. At large latitudes, the ratio of magnetic and gas
pressure is largest well behind the shock (
![]() ;
Fig. 21). Due to the rather extreme rotation of
the model, the high latitudes of the core are strongly rarefied, and the
shock propagates into a very thin medium near the axis, its structure
remaining unchanged.
;
Fig. 21). Due to the rather extreme rotation of
the model, the high latitudes of the core are strongly rarefied, and the
shock propagates into a very thin medium near the axis, its structure
remaining unchanged.
The GW amplitude of the weakly magnetized (![]() non-magnetic)
models A4B5G5-D3Mm (
non-magnetic)
models A4B5G5-D3Mm (![]() )
is characterized by a very large
negative amplitude at bounce (
)
is characterized by a very large
negative amplitude at bounce (
![]() ;
Fig. 19 and Table D.1). The signal is positive for several milliseconds after bounce due to the
aspherical shock wave, and approaches zero rapidly after the violent
re-expansion of the core. The bounce amplitude is significantly
lowered (
;
Fig. 19 and Table D.1). The signal is positive for several milliseconds after bounce due to the
aspherical shock wave, and approaches zero rapidly after the violent
re-expansion of the core. The bounce amplitude is significantly
lowered (
![]() )
in the
strongly magnetized model A4B5G5-D3M13 (Fig. 19 and
Table D.1), immediately after bounce the GW amplitude is
strongly positive and eventually becomes even more positive due to the
growing asphericity of the shock wave. The secondary collapse of this
models shows up in the GW amplitude in the form of a local minimum.
Afterwards the amplitude rises to values
)
in the
strongly magnetized model A4B5G5-D3M13 (Fig. 19 and
Table D.1), immediately after bounce the GW amplitude is
strongly positive and eventually becomes even more positive due to the
growing asphericity of the shock wave. The secondary collapse of this
models shows up in the GW amplitude in the form of a local minimum.
Afterwards the amplitude rises to values
![]() and shows superimposed very weak oscillations with a period of slightly less than 1 ms. In this model, the magnetic and the combined hydrodynamic plus gravitational amplitude contributions show a clear phase shift resulting from the opposing actions of hydrodynamic
(mainly centrifugal) and magnetic forces.
and shows superimposed very weak oscillations with a period of slightly less than 1 ms. In this model, the magnetic and the combined hydrodynamic plus gravitational amplitude contributions show a clear phase shift resulting from the opposing actions of hydrodynamic
(mainly centrifugal) and magnetic forces.
In all our models bouncing due to centrifugal forces the peak value of the GW signal at bounce decreases with increasing magnetic field strength, and for most models the ratio of the amplitudes of the post-bounce to the pre-bounce signal peaks decreases. Note that the latter statement must be considered carefully since - as discussed above - the GW signal may be subject to large modifications for models with very strong fields.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{4306f18a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg304.gif) |
Figure 18:
Model A2B4G1-D3M13 at
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.15cm,clip]{4306f19a.eps} \incl...
...306f19h.eps} \includegraphics[width=5.15cm,clip]{4306f19i.eps} }
\end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg305.gif) |
Figure 19:
Evolution of the rotational energy parameter
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4306f20a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg308.gif) |
Figure 20:
Comparison of two snapshots of model A4B5G5-D3M13. The innermost
region of the core is displayed at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4306f21a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg309.gif) |
Figure 21:
Model A4B5G5-D3M13 at
|
| Open with DEXTER | |
The magneto-rotational instability (MRI) is a shear instability
occurring in differentially rotating magnetized plasma, which generates
turbulence that amplifies the magnetic field and transfers angular
momentum (Balbus & Hawley 1998,1991,1992). If
effects due to buoyancy are neglected, a linear stability analysis shows
that the condition for the instability of a mode with wavenumber ![]() is
is
General theoretical considerations and non-linear simulations show that the magnetic energy achievable by the MRI field amplification process is of the order of the rotational energy, which is comparable to the saturation field expected from the process of winding-up field lines by differential rotation (Akiyama et al. 2003). However, in axisymmetric (non-linear) hydrodynamic simulations of accretion disks the field built up by the MRI was found to decay with a rate depending on the dissipation properties of the numerical scheme, and particularly on the grid resolution (Balbus & Hawley 1998,1991). This is due to Cowling's anti-dynamo theorem (Shercliff 1965) according to which an axisymmetric dynamo cannot work in a dissipative system, i.e. three-dimensional simulations are required.
In a star a convectively stable stratification will tend to stabilize
the MRI, while convective instability will strengthen the MRI.
Including the effects of buoyancy a mode with wave vector ![]() is
unstable with respect to the MRI in a weakly magnetized rotating system,
if the instability criterion
is
unstable with respect to the MRI in a weakly magnetized rotating system,
if the instability criterion
For decreasing wavenumber k (provided that
![]() )
the maximum growth rate (=
)
the maximum growth rate (=
![]() )
decreases approaching the value
)
decreases approaching the value
For a rotating magnetized configuration with axial symmetry the growth
time scale of the maximum growing MRI mode in the presence of entropy
gradients is given in spherical coordinates
![]() by
Akiyama et al. (2003)
by
Akiyama et al. (2003)
In order to see the MRI in our simulations, we must have sufficient
spatial resolution to resolve at least the modes with the longest
wavelengths which grow fastest. However, as these modes have the
smallest wavenumbers, the Alfvén velocity and thus the magnetic field
(parallel to the direction of ![]() )
must be sufficiently large for
the product
)
must be sufficiently large for
the product
![]() to be in the range of
maximum growth. This is unproblematic in the magneto-convective case
due to the large growth rate in the limit
to be in the range of
maximum growth. This is unproblematic in the magneto-convective case
due to the large growth rate in the limit
![]() .
In the magneto-shear limit only modes near
.
In the magneto-shear limit only modes near
![]() grow fast, which are,
however, difficult to resolve. Further numerical complications arise
from the fact that we have to identify the MRI in a very inhomogeneous
and highly dynamical background flow.
grow fast, which are,
however, difficult to resolve. Further numerical complications arise
from the fact that we have to identify the MRI in a very inhomogeneous
and highly dynamical background flow.
Apart from the direct solution of the MHD equations, there are alternative ways to investigate the MRI and the turbulence driven by the instability, such as the inclusion of well-suited models for turbulent transport coefficients into the momentum and energy equations. Various closure models for magnetorotational turbulence exist. The ones by Ogilvie (2003,2001) and Williams (2004,2005) which make use of the analogy of MHD turbulence with viscoelastic flows as observed, e.g. in polymer fluids in the laboratory, seem particularly interesting. Such methods provide a way for including turbulence effects into a numerical simulation that cannot treat these effects due to, e.g. resolution or symmetry constraints. However, in the simulations we report here, we did not consider any of these models. Instead, we focussed on the possibility of directly simulating the development of the instabilities.
In most of our models we find extended MRI unstable regions at various epochs. During collapse the cores are unstable in the magneto-shear limit. However, the growth times are significantly larger than the collapse time scale: even for the fastest growing mode they are of the order of a second (in the initial models). As the rotational energy and the degree of differential rotation increase during collapse, the growth times become smaller, but remains larger than the time until bounce, i.e. the dynamical background evolves faster than any unstable mode. Hence, we do not observe the growth of the MRI even for models where the initial magnetic field is sufficiently strong for magneto-shear modes to be numerically resolved.
During and shortly after bounce the cores possess a convectively stable
stratification, i.e. the MRI is of magneto-shear character. In model A1B3G3-D3M10 the immediate post-shock region is unstable shortly after shock formation due to a large negative angular velocity gradient (in ![]() -direction). The growth times are in the sub-millisecond to
millisecond range, i.e. comparable to the dynamic time scales. The
fastest growing modes correspond to spatial scales of less than 100 m, which are significantly smaller than the (local) grid
resolution of
-direction). The growth times are in the sub-millisecond to
millisecond range, i.e. comparable to the dynamic time scales. The
fastest growing modes correspond to spatial scales of less than 100 m, which are significantly smaller than the (local) grid
resolution of ![]() 300 m. For models with a stronger magnetic field
(e.g. A1B3G3-D3M12) the spatial scales of the fastest growing modes are
larger due to the larger Alfvén velocity, and they can be resolved.
However, they cannot be discriminated from the dynamic background flow
at the time of bounce which is dominated by numerous pressure waves
propagating through the inner core and launching the shock wave.
Moreover, obscuring the action of the MRI, the strong shear flow
surrounding the "surface'' of the inner core produces a strong toroidal
magnetic field component. The positive entropy gradient behind the shock
wave does not allow the MRI to grow in most of the post-shock region,
while large parts of the inner core are MRI unstable throughout the
entire post-bounce evolution due to the very flat entropy profile of
the core. However, as the instability is of magneto-shear nature, one
encounters the previously discussed spatial resolution problem unless
the magnetic field is already quite strong. The maximum growth rates
are moderate (
300 m. For models with a stronger magnetic field
(e.g. A1B3G3-D3M12) the spatial scales of the fastest growing modes are
larger due to the larger Alfvén velocity, and they can be resolved.
However, they cannot be discriminated from the dynamic background flow
at the time of bounce which is dominated by numerous pressure waves
propagating through the inner core and launching the shock wave.
Moreover, obscuring the action of the MRI, the strong shear flow
surrounding the "surface'' of the inner core produces a strong toroidal
magnetic field component. The positive entropy gradient behind the shock
wave does not allow the MRI to grow in most of the post-shock region,
while large parts of the inner core are MRI unstable throughout the
entire post-bounce evolution due to the very flat entropy profile of
the core. However, as the instability is of magneto-shear nature, one
encounters the previously discussed spatial resolution problem unless
the magnetic field is already quite strong. The maximum growth rates
are moderate (
![]() ms).
ms).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4306f22a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg335.gif) |
Figure 22:
Comparison of the evolution of models A1B3G3-D3M12 ( upper panels)
and A1B3G3-D3M10 ( lower panels). The left panels display the
total magnetic energy (solid lines) of the core, and the total
(dashed lines) and poloidal field energy (dash-dotted lines) of
the MRI-unstable regions, which are defined according to two different criteria: For the strong-field model A1B3G3-D3M12 all zones are considered where the growth time of the fastest growing mode is less than 10 ms, while for the weak-field model A1B3G3-D3M10 the corresponding magneto-convective limit is used. The energy density
|
| Open with DEXTER | |
Well after bounce when the shock wave begins to weaken and thus
(locally) negative entropy gradients develop, the MRI growth rates
become large even for long wavelengths (magneto-convective limit).
Thus, we observe the emergence of the corresponding modes, and a growth
of the vorticity
![]()
![]()
![]() of the flow.
However, this occurs late after bounce, when our assumptions concerning
the microphysics do no longer hold. For model A1B3G3-D3M10, we can
study the onset of magneto-convective modes. In regions where the
growth times of the MRI modes (in the limit
of the flow.
However, this occurs late after bounce, when our assumptions concerning
the microphysics do no longer hold. For model A1B3G3-D3M10, we can
study the onset of magneto-convective modes. In regions where the
growth times of the MRI modes (in the limit ![]() )
are less than 10 ms (Fig. 22), we find a rapid increase
of the magnetic energy, the magnetic energy density, and of the specific
magnetic energy. Their temporal variation can be described by
exponential laws in the interval
)
are less than 10 ms (Fig. 22), we find a rapid increase
of the magnetic energy, the magnetic energy density, and of the specific
magnetic energy. Their temporal variation can be described by
exponential laws in the interval
![]() .
In phases when the field is amplified by differential
rotation only, the toroidal field increases but the poloidal field and
the corresponding magnetic field energy stay approximately constant
(Fig. 22). However, when the MRI sets in,
the poloidal component grows too due to the stretching of the poloidal
field lines by meridional motions. Because of this behavior the two field amplification mechanisms can be distinguished.
.
In phases when the field is amplified by differential
rotation only, the toroidal field increases but the poloidal field and
the corresponding magnetic field energy stay approximately constant
(Fig. 22). However, when the MRI sets in,
the poloidal component grows too due to the stretching of the poloidal
field lines by meridional motions. Because of this behavior the two field amplification mechanisms can be distinguished.
For initially very strong magnetic fields (![]()
![]() ), the spatial scales of interest for the MRI can easily be resolved even in the magneto-shear limit, and the MRI criterion is
fulfilled the growth rates being similar to those of the weak-field
case. The proto-typical model A1B3G3-D3M12 shows the creation of a large amount of vorticity both in the post-shock gas and in the MRI unstable regions of the inner core (Fig. 7). Its vorticity is considerably larger than in the corresponding weak field model A1B3G3-D3M10, where we cannot resolve the growth of the
unstable modes due to their very small spatial scales. The flow is
organized in sheet-like structures which are typically a few kilometers
wide in
), the spatial scales of interest for the MRI can easily be resolved even in the magneto-shear limit, and the MRI criterion is
fulfilled the growth rates being similar to those of the weak-field
case. The proto-typical model A1B3G3-D3M12 shows the creation of a large amount of vorticity both in the post-shock gas and in the MRI unstable regions of the inner core (Fig. 7). Its vorticity is considerably larger than in the corresponding weak field model A1B3G3-D3M10, where we cannot resolve the growth of the
unstable modes due to their very small spatial scales. The flow is
organized in sheet-like structures which are typically a few kilometers
wide in ![]() -direction and
-direction and ![]() 10 km long in z-direction.
Another prominent flow structure forms near the equatorial plane in the
outer layers of the inner core, where a violent meridional flow leads to
the largest amplification of the poloidal field and to angular momentum
transport out of the inner core. The latter, which implies that the
loss of the rotational support of the inner core is caused by the MRI,
holds for all models where we can resolve the unstable modes, and where
the field is not too strong initially. For the extreme models AaBbGg-D3M13 the stress tensor is initially already large enough for
significant angular momentum transport to occur, i.e. only a very small
amount of field amplification is required.
10 km long in z-direction.
Another prominent flow structure forms near the equatorial plane in the
outer layers of the inner core, where a violent meridional flow leads to
the largest amplification of the poloidal field and to angular momentum
transport out of the inner core. The latter, which implies that the
loss of the rotational support of the inner core is caused by the MRI,
holds for all models where we can resolve the unstable modes, and where
the field is not too strong initially. For the extreme models AaBbGg-D3M13 the stress tensor is initially already large enough for
significant angular momentum transport to occur, i.e. only a very small
amount of field amplification is required.
Initially weak magnetic fields should lead to a similar dynamical
behavior, as the MRI does not depend on the initial field strength. The
modes should grow on similar time scales, but smaller spatial scales.
In practice, however, structures resolvable on our grid are much larger
than the wavelengths of the fastest growing modes, i.e. they have
relatively small growth rates. Hence, the development of the MRI is
artificially delayed. In addition, the smaller scales of the more
unstable modes may affect the global dynamics. Indeed, if we simulate
the evolution of model A1B3G3-D3M11 for a longer time, the poloidal
field energy starts to rise after
![]() ms. This rise is
accompanied by the formation of a flow pattern consisting of sheets of
large vorticity, and the extraction of rotational energy from the core,
quite similar to our findings for model A1B3G3-D3M12, though less
pronounced. Thus, the distinction between weak- and strong-field
models may be irrelevant, because even small initial fields give rise to
the same kind of instability and can become "strong'' according to our
criterion very rapidly.
ms. This rise is
accompanied by the formation of a flow pattern consisting of sheets of
large vorticity, and the extraction of rotational energy from the core,
quite similar to our findings for model A1B3G3-D3M12, though less
pronounced. Thus, the distinction between weak- and strong-field
models may be irrelevant, because even small initial fields give rise to
the same kind of instability and can become "strong'' according to our
criterion very rapidly.
The poloidal field strength oscillates similarly as the density or the rotational energy during the post-bounce phase for the models bouncing due to centrifugal forces. The field is subject to compression and expansion, but apart from the oscillations it does not grow unless an MRI-like mechanism sets in.
The magneto-convective motions found during the later stages of weak field models are much less pronounced in the cores of strong field ones. There are two reasons for this behavior: Firstly, due to the extraction of angular momentum from the core one of the driving forces of the instability is reduced, and secondly a strong magnetic field is known to suppress convection. The latter also holds for the MRI which is hampered by too strong fields, as the seed field cannot be amplified beyond the MRI saturation value. This can be seen from Eq. (23): for large Alfvén velocities only modes with very long wavelengths (or small wavenumbers) are unstable. If the critical wavelength exceeds the intrinsic scales of the problem, e.g. the size of the inner core or the size of potentially unstable regions, the unstable longer modes cannot develop, and the modes of smaller wavelengths are stable.
The dynamics and gravitational wave signature of the models A3B3G5-DdM12 differing only in the location of the field-generating current loop (i.e. in their Dd parameter; see Sect. 2.3.3) are qualitatively quite similar, except for model A3B3G5-D0M12 whose current loop is located at infinity (see the discussion below). The time scale for the slow-down of the core exhibits some variation, but otherwise the evolution and the GW signal agree qualitatively quite well with those of the corresponding reference models A3B3G5-D3Mm (see above). This may be surprising because the initial total magnetic energies of models having uniform fields may be more than 100 times greater than that of current-loop models (Table 2). However, the outer parts of the very extended field structure of the more strongly magnetized models, where most of the additional magnetic energy is stored, are dynamically less important than the central regions, and in particular the region around the field-generating current loop where the magnetic field is strongest.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{4306f23a.eps} \end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg340.gif) |
Figure 23:
The post-shock region of models A3B3G5-D0M12 ( left quadrants) and A3B3G5-D2M12 ( right quadrants) at
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.6cm,clip]{4306f24a.eps} \inclu...
...]{4306f24e.eps} \includegraphics[width=5.6cm,clip]{4306f24f.eps} }
\end{figure}](/articles/aa/full/2006/18/aa4306-05/Timg341.gif) |
Figure 24: The evolution of the maximum density ( top panels) and the GW amplitude ( bottom panels) of models A3B3G3-D0M13 ( left panels), A3B3G3-D3M13 ( middle panels), and A3B3G3-D1M13 ( right panels), respectively. The GW signal of model A3B3G3-D0M13 shows a constant offset from zero, which is subtracted here. |
| Open with DEXTER | |
For the initially homogeneously magnetized model A3B3G5-D0M12 a less
efficient braking of the core's rotation is observed than for the
corresponding current-loop models. Instead of a contracting secularly,
the core expands to sub-nuclear densities on a comparable time scale.
The rotation energy of the immediate post-bounce core of model A3B3G5-D0M12 is slightly smaller (
![]() at
at
![]() )
than for the corresponding non-magnetic core (
)
than for the corresponding non-magnetic core (
![]() at
at
![]() ), and it decreases sightly during the subsequent evolution.
Although the magnetic field gets amplified a little during collapse,
), and it decreases sightly during the subsequent evolution.
Although the magnetic field gets amplified a little during collapse,
![]() decreases until bounce because most efficient
amplification takes place in the central regions of the core whereas the
total magnetic energy is dominated by the outer regions where the field
stays roughly constant during collapse. Afterwards, both
decreases until bounce because most efficient
amplification takes place in the central regions of the core whereas the
total magnetic energy is dominated by the outer regions where the field
stays roughly constant during collapse. Afterwards, both
![]() and
and
![]() show a comparable growth
to the current-loop models, and the ratio of toroidal field energy and
total field energy grows steadily, but slowly. The magnetic field of the
uniformly magnetized core has a simpler structure at late times, while
the current-loop fields become more and more twisted. The gravitational
wave amplitude of model A3B3G5-D0M12 is strongly dominated by the fluid
contribution in spite of its large initial magnetic energy, and
resembles that of the corresponding current-loop cores in many respects.
The small magnetic contribution to the signal never exceeds that of
model A3B3G5-D3M12, although this model has a 15 times smaller magnetic
energy (but the same central field strength).
show a comparable growth
to the current-loop models, and the ratio of toroidal field energy and
total field energy grows steadily, but slowly. The magnetic field of the
uniformly magnetized core has a simpler structure at late times, while
the current-loop fields become more and more twisted. The gravitational
wave amplitude of model A3B3G5-D0M12 is strongly dominated by the fluid
contribution in spite of its large initial magnetic energy, and
resembles that of the corresponding current-loop cores in many respects.
The small magnetic contribution to the signal never exceeds that of
model A3B3G5-D3M12, although this model has a 15 times smaller magnetic
energy (but the same central field strength).
Model A3B3G5-D2M12 has an initial magnetic field energy which is a factor of 150 greater than that of model A3B3G5-D0M12 (Table 2). Nevertheless, at
![]() ,
its
magnetic field is almost three times as energetic as that of model A3B3G5-D0M12 (
,
its
magnetic field is almost three times as energetic as that of model A3B3G5-D0M12 (
![]() compared to
compared to
![]() )
due to the different amount of field
amplification occurring in both cases. At bounce both models have
developed a region of high magnetization near the edge of the inner core
close to the rotation axis. In model A3B3G5-D2M12 this region also
extends towards larger radii along the equatorial plane forming a highly
magnetized "sheet'' which is a relic of the initially highly magnetized
region around the field generating current-loop. The shape of the
shock waves is similar in both models, but the regions of large magnetic
pressure are more extended in the current-loop model filling the whole
post-shock region, whereas they are more concentrated towards the very
center of the core for the uniform field model
(Fig. 23).
)
due to the different amount of field
amplification occurring in both cases. At bounce both models have
developed a region of high magnetization near the edge of the inner core
close to the rotation axis. In model A3B3G5-D2M12 this region also
extends towards larger radii along the equatorial plane forming a highly
magnetized "sheet'' which is a relic of the initially highly magnetized
region around the field generating current-loop. The shape of the
shock waves is similar in both models, but the regions of large magnetic
pressure are more extended in the current-loop model filling the whole
post-shock region, whereas they are more concentrated towards the very
center of the core for the uniform field model
(Fig. 23).
Similar trends as for model series A3B3G5-DdM12 can be observed in the
case of model series A3B3G3-DdM13 (Fig. 24). The dynamics
of the current-loop model A3B3G3-D1M13 is qualitatively comparable to
that of a A3B3G3-D3Mm model with a much weaker magnetic field. Hence,
its GW signal does not differ much from the non-magnetic case in spite
of its strong initial magnetic field. However, we find large
differences between the uniform field model A3B3G3-D0M13
(Fig. 24, left panels) and the current-loop models, as
e.g. A3B3G3-D3M13 (Fig. 24, middle panels). The maximum
density of the former model exhibits large-scale pulsations during
which the bounce density is exceeded by ![]() ,
and
,
and
![]() is smaller than
is smaller than
![]() for most of the time. The core has a very high magnetic energy initially,
for most of the time. The core has a very high magnetic energy initially,
![]() ,
which decreases during the
collapse until it levels off at
,
which decreases during the
collapse until it levels off at ![]()
![]() .
This value is still
much larger than the largest one reached by the current-loop models
during their whole evolution. The GW signature of model A3B3G3-D0M13
reflects the density oscillations of the core, and like in the case of
model A3B3G3-D3M13, it is considerably shifted towards positive
amplitudes (Fig. 24) due to the very aspherical shape of
the shock wave.
.
This value is still
much larger than the largest one reached by the current-loop models
during their whole evolution. The GW signature of model A3B3G3-D0M13
reflects the density oscillations of the core, and like in the case of
model A3B3G3-D3M13, it is considerably shifted towards positive
amplitudes (Fig. 24) due to the very aspherical shape of
the shock wave.
Past and present realistic studies of core collapse supernovae neglect magnetic fields. Instead, they focus on an elaborate and accurate description of the microphysics and (neutrino) transport physics. Since this is a formidable task requiring extensive computational resources, these studies are necessarily limited to a very small number of different initial models. Bearing in mind our lack of knowledge of the exact conditions in the pre-collapse star, we pursued a complimentary approach. Instead of simulating the evolution of a few stars in great detail, we performed a comprehensive parameter study covering the space of possible progenitors with a large number of initial models and exploring a relatively unknown territory, namely the influence of magnetic fields. Consequently, we are restricted to some simplified and approximate treatment of the core's physics, and employ only simplified progenitor models (i.e. polytropes).
Our parameter study focuses on the investigation of two main questions:
Our simulations show significant modifications of the dynamics and the
GW signal of strongly magnetized cores compared to non-magnetic ones.
Magnetic fields are amplified in some of our models to very large field
strengths which are in the magnetar range (
![]() ). Such strong magnetic fields efficiently extract rotational
energy from the central core, thereby triggering a secular post-bounce
contraction phase. They also cause the formation of collimated
outflows, which give rise to distinctive features in the GW signal.
Hence, it is in principle possible to extract information about the
degree to which an explosion has a jet-like character from the GW signal. Further specific results are:
). Such strong magnetic fields efficiently extract rotational
energy from the central core, thereby triggering a secular post-bounce
contraction phase. They also cause the formation of collimated
outflows, which give rise to distinctive features in the GW signal.
Hence, it is in principle possible to extract information about the
degree to which an explosion has a jet-like character from the GW signal. Further specific results are:
Imposing axial (and equatorial) symmetry is a serious restriction when simulating MHD flows. It prevents us from investigating the fate of cores whose magnetic field and rotational axis are misaligned as in pulsars, and from simulating the intrinsically 3D magneto-rotational instability to the full extent. We think that the first shortcoming will influence our results only slightly, as the initial magnetic field is soon completely dominated in our models by the field generated by differential rotation. Thus, provided there is a poloidal seed field of similar strength no significant changes are to be expected. The second restriction is probably uncritical for the relatively short time scales covered by our simulations, as the dominant amplification process for the magnetic field during these early stages is the rapid winding-up of the initial poloidal field by means of differential rotation. Additional field growth by the MRI or other MHD instabilities is probably less important. In any case, limited by the present computational resources, a 3D MHD parameter study of core collapse is still some years ahead.
A further limitation arises from our Newtonian approach, as we observe
outflow velocities in some of our models that exceed ![]()
![]() of
the speed of light and that are still increasing when we had to stop our
simulations. Although being only mildly relativistic in our models, a
study of the further evolution of these outflows may require a special
relativistic MHD code, if the jets continue to accelerate. The effects
of general relativistic corrections of the gravitational potential on
magneto-rotational core collapse arising due to the high compactness of
the collapsed cores have been investigated by us in some detail. The
results of this complementary study will be presented in a separate
publication.
of
the speed of light and that are still increasing when we had to stop our
simulations. Although being only mildly relativistic in our models, a
study of the further evolution of these outflows may require a special
relativistic MHD code, if the jets continue to accelerate. The effects
of general relativistic corrections of the gravitational potential on
magneto-rotational core collapse arising due to the high compactness of
the collapsed cores have been investigated by us in some detail. The
results of this complementary study will be presented in a separate
publication.
Acknowledgements
MO thanks H. Dimmelmeier for help in preparing, performing and understanding these simulations, particularly for providing the routines to compute the hydrodynamic initial models. Part of the simulations were performed at the Rechenzentrum Garching (RZG) of the Max-Planck-Gesellschaft. MAA is a Ramón y Cajal Fellow of the Spanish Ministry of Education and Science. MAA acknowledges the partial support of the Spanish Ministerio de Ciencia y Tecnología (AYA2004-08067-C03-C01) and of the Sonderforschungsbereich-Transregio 7 "Gravitationswellenastronomie'' of the German Ministry of Science.
In this section we summarize the basics of the relaxing TVD method. For further information the reader is referred to Pen et al. (2003), Jin & Xin (1995), Trac & Pen (2003).
A major drawback of MUSCL-type and Riemann solver schemes for systems
of non-linear conservation laws is the need for calculating the
eigenvalues am, and the eigenvectors of the Jacobian of the flux
vector (Hebrew indices
![]() enumerate the
components of the system of m equations)
enumerate the
components of the system of m equations)
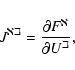 |
(A.1) |
To ensure the numerical convergence of our results, we performed a number of simulations of the same model using different grid spacings.
Based on these simulations, we selected a grid of 380 zones in radial
and 60 zones in angular direction as our standard grid. The grid is
logarithmically spaced in radius, with a central resolution of
![]() and a relative
increase of the cell size from zone to the zone of
and a relative
increase of the cell size from zone to the zone of ![]()
![]() .
The angular grid is uniform.
.
The angular grid is uniform.
Results from a sample of the convergence runs are displayed in
Fig. B.1. We show the temporal evolution of the
maximum density, the GW amplitude, and
![]() for model A1B3G3-D3M13, computed with grids of
for model A1B3G3-D3M13, computed with grids of
Since we do not evolve the consistent set of general-relativistic MHD equations, we are not able to extract the GW signal from the metric. But, in the post-Newtonian limit, it is still possible to extract the lowest-order terms of the GW signal from the hydrodynamic variables. For this purpose we have used the reformulation of the quadrupole formula by Mönchmeyer et al. (1991), where temporal derivatives are replaced by spatial ones using the continuity and the Euler equations. Thus, the hydrodynamic fluxes and source terms are introduced into the quadrupole formula.
As we use spherical coordinates
![]() in our simulations,
the metric perturbation associated with a gravitational wave is most
conveniently expanded in terms of pure spin tensor harmonics
in our simulations,
the metric perturbation associated with a gravitational wave is most
conveniently expanded in terms of pure spin tensor harmonics
![]() and
and
![]() with the corresponding "electric'' and "magnetic'' amplitudes
with the corresponding "electric'' and "magnetic'' amplitudes
![]() and
and
![]() ,
respectively:
,
respectively:
hab = 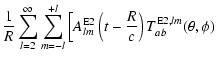 |
(B.1) |
 |
(B.2) |
 |
|||
| (B.5) | |||
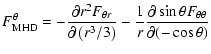 |
|||
| (B.6) | |||
| (B.7) | |||
| (B.8) |
| (B.9) |
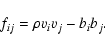 |
(B.11) |
Equation (C.10) corresponds to the hydrodynamic and the Lorentz force parts of the quadrupole formula given by
Kotake et al. (2004b), who derived the following
expression for the GW amplitude
![]() :
:
To evaluate these expressions, the current density ![]() and the
electric field
and the
electric field ![]() have to be calculated from the magnetic field
and the velocity. The last term (Eq. (C.14)) describes the
contribution resulting from the energy density of the magnetic field.
Kotake et al. (2004b) found that the hydrodynamic
and the Lorentz force contributions are at least two orders of magnitude
larger than the magnetic energy one. Therefore, and due to the time
derivatives still involved in its calculation, we neglect this
contribution and consider only the GW amplitude resulting from the
quadrupole moment of the matter.
have to be calculated from the magnetic field
and the velocity. The last term (Eq. (C.14)) describes the
contribution resulting from the energy density of the magnetic field.
Kotake et al. (2004b) found that the hydrodynamic
and the Lorentz force contributions are at least two orders of magnitude
larger than the magnetic energy one. Therefore, and due to the time
derivatives still involved in its calculation, we neglect this
contribution and consider only the GW amplitude resulting from the
quadrupole moment of the matter.
Tables D.1 through D.2 provide an overview of the dynamic evolution of the flow and the magnetic field, and about the resulting gravitational wave signal of all our models.
Table D.1:
Some characteristic model quantities: the first two columns give the model name and the
classification of the GW signal (for the corresponding
non-magnetized model). Columns 3 and 4 give the time of bounce
![]() (in milliseconds) and the maximum density at bounce
(in milliseconds) and the maximum density at bounce
![]() (in units of
(in units of
![]() ). An exclamation mark behind the density value signifies that the maximum density of
the model exceeds the bounce density during the later evolution.
). An exclamation mark behind the density value signifies that the maximum density of
the model exceeds the bounce density during the later evolution.
![]() (Col. 5) and
(Col. 5) and
![]() (Col. 6) are the maximum GW amplitude (in cm) and
the corresponding magnetic contribution.
(Col. 6) are the maximum GW amplitude (in cm) and
the corresponding magnetic contribution.
![]() (Col. 7) is a rough mean value of the wave
amplitude (in cm) at some late epoch; no value is provided when the
GW amplitude does not approach a quasi-constant asymptotic value.
If the absolute value of this amplitude is large, the presence of an aspheric outflow at late epochs can be inferred. The following columns give the maximum value of the rotational (Col. 8) and the magnetic beta parameter (Col. 9), the time when
(Col. 7) is a rough mean value of the wave
amplitude (in cm) at some late epoch; no value is provided when the
GW amplitude does not approach a quasi-constant asymptotic value.
If the absolute value of this amplitude is large, the presence of an aspheric outflow at late epochs can be inferred. The following columns give the maximum value of the rotational (Col. 8) and the magnetic beta parameter (Col. 9), the time when
![]() reaches its maximum (Col. 10), and the corresponding beta of the toroidal field (Col. 11). If the
magnetic field is still amplifying at the end of the simulation, an exclamation mark is added behind the table entry, and if the magnetic field is decreasing at this time, we give its final
value
reaches its maximum (Col. 10), and the corresponding beta of the toroidal field (Col. 11). If the
magnetic field is still amplifying at the end of the simulation, an exclamation mark is added behind the table entry, and if the magnetic field is decreasing at this time, we give its final
value
![]() in parentheses.
in parentheses.
Table D.2:
Some characteristic model quantities (name of model given in Col. 1) at time t (in
msec; Col. 2) when the core has reached a quasi-equilibrium
state. For models which do not reach a quasi-equilibrium state
until the end of the simulation (e.g. type-II models with large
scale core pulsations) we provide upper (top value) and lower
(bottom value) bounds estimated from the values at maximum and
minimum contraction. Columns 3 and 4 give the surface radius
![]() (in km) and the mass
(in km) and the mass
![]() (in solar masses) of the quasi-equilibrium configuration, respectively.
Since it is still surrounded by an (expanding) envelope of high
density matter, the definition of its surface radius
(in solar masses) of the quasi-equilibrium configuration, respectively.
Since it is still surrounded by an (expanding) envelope of high
density matter, the definition of its surface radius
![]() is somewhat uncertain. As the rotation rate
is somewhat uncertain. As the rotation rate
![]() (in ms), where
(in ms), where ![]() is the angular velocity
averaged over the angle
is the angular velocity
averaged over the angle ![]() ,
as well as the total magnetic
field
,
as well as the total magnetic
field ![]() and (the absolute value of) its toroidal component
and (the absolute value of) its toroidal component
![]() (both in Gauss) vary strongly near the surface and on short time scales, the corresponding values in Cols. 5-7 should be used with care. Negative values of the rotation
rate signify counter-rotating cores. Finally, in Cols. 8 and 9
we give the radii of the shock at the polar axis,
(both in Gauss) vary strongly near the surface and on short time scales, the corresponding values in Cols. 5-7 should be used with care. Negative values of the rotation
rate signify counter-rotating cores. Finally, in Cols. 8 and 9
we give the radii of the shock at the polar axis,
![]() ,
and at the equator,
,
and at the equator,
![]() (both in cm), respectively. No entry
in these columns implies that the shock has already left the
computational grid.
(both in cm), respectively. No entry
in these columns implies that the shock has already left the
computational grid.