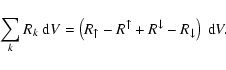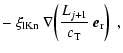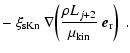Up: Dust in brown dwarfs
Subsections
5 Moment method for nucleation, growth, evaporation and
equilibrium drift
The physical and chemical processes discussed so far (nucleation,
growth, evaporation, gravitational settling and element
depletion/enrichment) occur simultaneously in the atmosphere and may
be strongly coupled. Therefore, our aim in this section is to derive a
consistent time-dependent description of the dust component in
brown dwarf or giant gas planet atmospheres. We will
derive a system of partial differential equations which describes the
evolution of the dust component by means of the moments of its size
distribution function. This idea was originally developed by
Gail
 Sedlmayr (1988) and extended by Dominik
Sedlmayr (1988) and extended by Dominik
 (1993) to core-mantle and dirty grains. The
resulting differential equations are supposed to be simple and
includable into hydrodynamics or classical stellar atmosphere
calculations. In contrast, we want to avoid an elaborate and
time-consuming multi-component treatment of the dust component, e.g.by
using discrete bins for the dust size distribution function with
individual drift velocities in this paper.
(1993) to core-mantle and dirty grains. The
resulting differential equations are supposed to be simple and
includable into hydrodynamics or classical stellar atmosphere
calculations. In contrast, we want to avoid an elaborate and
time-consuming multi-component treatment of the dust component, e.g.by
using discrete bins for the dust size distribution function with
individual drift velocities in this paper.
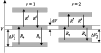 |
Figure 5:
Two surface chemical processes (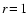 and
and 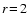 )
populating or depopulating an infinitesimal dust grain volume
interval )
populating or depopulating an infinitesimal dust grain volume
interval
![$[V,V\!+\!{\rm d}V]$](/articles/aa/full/2003/07/aah3912/img338.gif) . . |
The master equation for dust particles
![$\in\![V,V\!+\!{\rm d}V]$](/articles/aa/full/2003/07/aah3912/img340.gif) ,
,
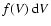 ,
where
,
where
![$f(V)~\rm [cm^{-6}]$](/articles/aa/full/2003/07/aah3912/img342.gif) is the distribution function of
dust particles in volume space, is given by
is the distribution function of
dust particles in volume space, is given by
![\begin{displaymath}\frac{{\rm\partial} }{{\rm\partial} t}\big(f(V)~{\rm d}V\big)...
...rc}}(V)\big]f(V)~{\rm d}V\!\Big) = \sum\limits_k R_k~{\rm d}V.
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img343.gif) |
(55) |
The r.h.s. of Eq. (55) expresses the population and depopulation
of the considered volume interval
![$[V,V\!+\!{\rm d}V]$](/articles/aa/full/2003/07/aah3912/img338.gif) with dust particles which
are changing their size due to accretion or evaporation of molecules
(see Fig. 5),
with dust particles which
are changing their size due to accretion or evaporation of molecules
(see Fig. 5),
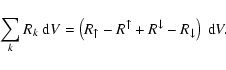 |
(56) |
Multiplication of Eq. (55) with Vj/3 (
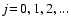 )
and integration over V from a lower integration boundary
)
and integration over V from a lower integration boundary
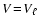 to
to
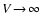 results in
results in
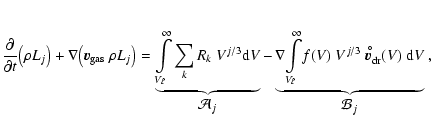 |
|
|
(57) |
where the jth moment of the dust size distribution function
![$L_
j~{\rm [cm}^j\!/{\rm g]}$](/articles/aa/full/2003/07/aah3912/img349.gif) is defined by
is defined by
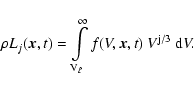 |
(58) |
The source term
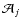 expresses the effects of surface chemical
reactions on the dust moments and
expresses the effects of surface chemical
reactions on the dust moments and
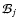 is an additional, advective
term in the dust moment equations which comprises the effects
caused by a size-dependent drift motion of the grains, e.g.due to gravity.
is an additional, advective
term in the dust moment equations which comprises the effects
caused by a size-dependent drift motion of the grains, e.g.due to gravity.
The maximum grain sizes to be expected in brown dwarf atmospheres
(Fig. 3) allow us to concentrate on two major cases in
the following, namely the subsonic free molecular flow and the
laminar viscous flow.
5.1 Subsonic free molecular flow
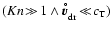
For large Knudsen numbers, the chemical rates depicted in
Fig. 5 can be expressed according to Eq. (22):
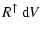 |
= |
![$\displaystyle \sum\limits_{\rm r} f(V)~{\rm d}V~4\pi[a(V)]^2~
n_{\rm r} v^{\rm rel}_{\rm r} \alpha_{\rm r}$](/articles/aa/full/2003/07/aah3912/img355.gif) |
(59) |
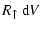 |
= |
![$\displaystyle \sum\limits_{\rm r} f(V\!-\!\Delta V_{\rm r})~{\rm d}V~4\pi\!
\le...
...V\!-\!\Delta V_{\rm r})\right]^2\!
n_{\rm r} v^{\rm rel}_{\rm r} \alpha_{\rm r}$](/articles/aa/full/2003/07/aah3912/img357.gif) |
(60) |
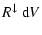 |
= |
![$\displaystyle \sum\limits_{\rm r} f(V\!+\!\Delta V_{\rm r})~{\rm d}V~4\pi [a(V)]^2~
n_{\rm r} v^{\rm rel}_{\rm r} \alpha_{\rm r} \frac{1}{S_{\rm r}}$](/articles/aa/full/2003/07/aah3912/img359.gif) |
(61) |
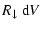 |
= |
![$\displaystyle \sum\limits_{\rm r} f(V)~{\rm d}V~
4\pi\!\left[a(V\!-\!\Delta V_{...
...\right]^2
n_{\rm r} v^{\rm rel}_{\rm r} \alpha_{\rm r} \frac{1}{S_{\rm r}}\cdot$](/articles/aa/full/2003/07/aah3912/img361.gif) |
(62) |
Applying detailed balance considerations (Milne relations),
Gauger
 (1990) and Patzer
(1990) and Patzer
 (1998) have
shown that for simple types of surface reactions, denoted by
homogeneous and heterogeneous growth, the (inverse) evaporation rates
can be expressed by the related (forward) growth rates and the
supersaturation ratio in the way written in Eqs. (61) and
(62). For Eqs. (59) and (60), we
have neglected a possible influence of a fast drift motion on the
growth rates and for Eqs. (61) to (62), we
have assumed thermal equilibrium (dust temperature
(1998) have
shown that for simple types of surface reactions, denoted by
homogeneous and heterogeneous growth, the (inverse) evaporation rates
can be expressed by the related (forward) growth rates and the
supersaturation ratio in the way written in Eqs. (61) and
(62). For Eqs. (59) and (60), we
have neglected a possible influence of a fast drift motion on the
growth rates and for Eqs. (61) to (62), we
have assumed thermal equilibrium (dust temperature 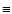 gas
temperature) and chemical equilibrium among the molecules in the gas
phase.
gas
temperature) and chemical equilibrium among the molecules in the gas
phase.
Solving Eq. (19) with the frictional force according
to Eq. (13, subsonic case) the equilibrium drift
velocity is
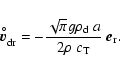 |
(63) |
By means of the Eqs. (59) to (63), the
integrals on the r.h.s. of Eq. (57) can be evaluated as
shown in more detail concerning the term
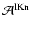 in
(Gail
in
(Gail
 Sedlmayr 1988). After some algebraic manipulations,
including
Sedlmayr 1988). After some algebraic manipulations,
including
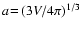 ,
the approximation
,
the approximation
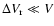 and
partial integration, the results are
and
partial integration, the results are
where
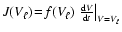 is the
current of dust particles in volume space at the lower integration
boundary. In case of net growth,
is the
current of dust particles in volume space at the lower integration
boundary. In case of net growth,
![$J({V_{\ell}})~\rm [cm^{-3}s^{-1}]$](/articles/aa/full/2003/07/aah3912/img372.gif) can be
identified with the stationary nucleation rate
can be
identified with the stationary nucleation rate 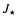 (Gail
(Gail
 Sedlmayr 1988). The characteristic growth speed
Sedlmayr 1988). The characteristic growth speed
![$\chi_{\rm lKn}^{\rm
net}~\rm [cm/s]$](/articles/aa/full/2003/07/aah3912/img374.gif) (an increase of radius per time) and the
characteristic gravitational force density
(an increase of radius per time) and the
characteristic gravitational force density
![$\xi_{\rm lKn}~\rm
[{\rm d}yn/cm^3]$](/articles/aa/full/2003/07/aah3912/img375.gif) are given by
are given by
5.2 Laminar viscous flow
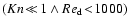
The derivation of the moment equations for the case of small Knudsen numbers
is analogous to the previous subsection. We express the surface chemical
rates according to Eq. (32) by
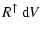 |
= |
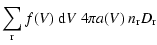 |
(68) |
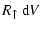 |
= |
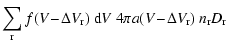 |
(69) |
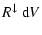 |
= |
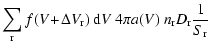 |
(70) |
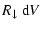 |
= |
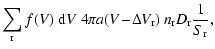 |
(71) |
again neglecting the influence of drift on growth and assuming
thermal and chemical equilibrium. The equilibrium drift velocity results
from Eq. (19) with the frictional force according to
Eq. (16, small
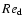 case)
case)
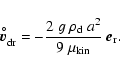 |
(72) |
By repeating the procedure of the last subsection, the r.h.s. terms
of the dust moment equations are
The characteristic growth speed
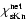 has now the
unit [cm2 s-1] (an increase of surface per time) whereas the
characteristic gravitational force density
has now the
unit [cm2 s-1] (an increase of surface per time) whereas the
characteristic gravitational force density
 remains the same
except for a different geometry factor.
remains the same
except for a different geometry factor.


Up: Dust in brown dwarfs
Copyright ESO 2003
![]() Sedlmayr (1988) and extended by Dominik
Sedlmayr (1988) and extended by Dominik
![]() (1993) to core-mantle and dirty grains. The
resulting differential equations are supposed to be simple and
includable into hydrodynamics or classical stellar atmosphere
calculations. In contrast, we want to avoid an elaborate and
time-consuming multi-component treatment of the dust component, e.g.by
using discrete bins for the dust size distribution function with
individual drift velocities in this paper.
(1993) to core-mantle and dirty grains. The
resulting differential equations are supposed to be simple and
includable into hydrodynamics or classical stellar atmosphere
calculations. In contrast, we want to avoid an elaborate and
time-consuming multi-component treatment of the dust component, e.g.by
using discrete bins for the dust size distribution function with
individual drift velocities in this paper.

![]() ,
,
![]() ,
where
,
where
![]() is the distribution function of
dust particles in volume space, is given by
is the distribution function of
dust particles in volume space, is given by