A fundamental process for the consideration of the time-dependent
behaviour of the dust component in brown dwarf atmospheres is the
growth of the dust particles by accretion of molecules. The
respective reverse process (thermal evaporation, in view of more
complex surface reactions also sometimes denoted by chemical
sputtering) is important at high temperatures![]() . Considering the thermodynamical conditions
in brown dwarf atmospheres, we are again faced with the problem of
qualitative changes of the dynamical behaviour of the gas component
due to different Knudsen numbers.
. Considering the thermodynamical conditions
in brown dwarf atmospheres, we are again faced with the problem of
qualitative changes of the dynamical behaviour of the gas component
due to different Knudsen numbers.
For large Knudsen numbers (lKn), gas molecules of all kinds are freely
impinging onto the surface of the grain. Some of these dust-molecule
collisions (sometimes a certain sequence of them) will initiate a chemical
surface reaction which causes a growth step (or an evaporation step) of the
dust particle. This case has been extensively studied in the circumstellar
envelopes of AGB stars (Gail
![]() Sedlmayr 1988; Gauger
Sedlmayr 1988; Gauger
![]() 1990;
Dominik
1990;
Dominik
![]() 1993).
1993).
The accretion rate, expressed in terms of the increase of the
particle's volume
![]() due to chemical surface
reactions for large Knudsen numbers is given by
due to chemical surface
reactions for large Knudsen numbers is given by
The last term on the r.h.s. of Eq. (22) takes into
account the reverse chemical processes, namely the thermal evaporation
rates. It determines the sign of
![]() and hence decides whether
the dust particle grows or shrinks.
and hence decides whether
the dust particle grows or shrinks.
![]() is
a generalised supersaturation ratio of the surface reaction "r''
(Dominik
is
a generalised supersaturation ratio of the surface reaction "r''
(Dominik
![]() 1993) where
1993) where
![]() is the particle density of the key
species in phase-equilibrium over the condensed dust material.
is the particle density of the key
species in phase-equilibrium over the condensed dust material.
![]() is not known a priori. In the case of simple surface
reactions, which transform
is not known a priori. In the case of simple surface
reactions, which transform ![]() units of the solid material
units of the solid material ![]() from the gaseous into the condensed phase (and vice versa), e.g.
from the gaseous into the condensed phase (and vice versa), e.g.
![]() (
(
![]() ,
,
![]() )
or
)
or
![]() (
(
![]() ,
,
![]() ), the generalised
supersaturation ratio
), the generalised
supersaturation ratio ![]() is related to the usual supersaturation ratio
is related to the usual supersaturation ratio
![]() of the dust grain
material
of the dust grain
material ![]() (Gauger
(Gauger
![]() 1990) by
1990) by
| (23) |
For small Knudsen numbers (sKn), the transport of gas molecules to the
surface of the grain (or the transport of evaporating molecules away
from the grain's surface) is not a simple free flight with thermal
velocity as assumed in Eq. (22), but is hindered by
inter-molecular collisions. Consequently, the grain growth and
evaporation is limited by the diffusion of molecules towards or away
from the grain's surface, considering growth or evaporation in the
laminar case, respectively (we disregard here convection as transport
process for the molecules, expected to occur in the turbulent case).
We consider the following particle conservation equation with a
diffusive transport term (see Landau & Lifschitz 1987, Eq. (38.2)
ff)
Considering the static case (
![]() )
and assuming stationary
(
)
and assuming stationary
(
![]() )
and spherical symmetry,
Eq. (24) results in
)
and spherical symmetry,
Eq. (24) results in
The solution of Eq. (28) with the boundary
conditions (29) and (30) is
For arbitrary Knudsen numbers we apply the same interpolation scheme
as outlined in Sect. 2.3. We define a critical Knudsen
number
![]() by equating Eqs. (22) with (32)
by equating Eqs. (22) with (32)
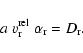 |
(33) |
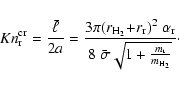 |
(34) |
| (35) |
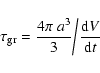 |
(37) |
The particle growth is found to be typically 3 orders of magnitude
slower than the acceleration which allows us to assume instantaneous
acceleration (equilibrium drift). For large Knudsen numbers, we find
![]() whereas for small Knudsen numbers
the growth time-scale increases faster for larger grains and becomes
density-independent,
whereas for small Knudsen numbers
the growth time-scale increases faster for larger grains and becomes
density-independent,
![]() .
Note that the
influence of the drift velocities on the particle growth has not been
considered in Eqs. (22) and (32) such
that for supersonic drift velocities or large dust Reynolds numbers, the
presented physical description is not valid.
.
Note that the
influence of the drift velocities on the particle growth has not been
considered in Eqs. (22) and (32) such
that for supersonic drift velocities or large dust Reynolds numbers, the
presented physical description is not valid.
An additional dashed line is depicted in Fig. 3, where
![]() .
This line defines a maximum dust
grain size
.
This line defines a maximum dust
grain size
![]() in a brown dwarf atmosphere. For larger
particles (
in a brown dwarf atmosphere. For larger
particles (
![]() above the dashed line), the growth
time-scale exceeds the time-scale for gravitational settling
(
above the dashed line), the growth
time-scale exceeds the time-scale for gravitational settling
(
![]() )
which means that such particles
are already removed from the atmosphere before they can be formed.
Consequently, such particles cannot exist. The maximum grain size
)
which means that such particles
are already removed from the atmosphere before they can be formed.
Consequently, such particles cannot exist. The maximum grain size
![]() varies between
varies between ![]() 1
1 ![]() m in the thin, outer
atmospheric regions (
m in the thin, outer
atmospheric regions (
![]() )
and
)
and
![]() 100
100 ![]() m in the dense, inner regions
(
m in the dense, inner regions
(
![]() ). These values depend on the stellar
parameters and the considered dust material density.
). These values depend on the stellar
parameters and the considered dust material density.
Note, that an absolute minimum of
![]() has been
considered in Fig. 3 since extreme supersaturation
(
has been
considered in Fig. 3 since extreme supersaturation
(
![]() )
and solar abundance of silicon in the gas phase
have been assumed. In the case of an Si-depleted or nearly saturated
gas (
)
and solar abundance of silicon in the gas phase
have been assumed. In the case of an Si-depleted or nearly saturated
gas (![]() ),
),
![]() becomes larger and the maximum
particle radius
becomes larger and the maximum
particle radius
![]() becomes smaller. Furthermore, the
values for
becomes smaller. Furthermore, the
values for
![]() are relatively independent of temperature,
but will shift as
are relatively independent of temperature,
but will shift as
![]() in the free molecular flow
case and
in the free molecular flow
case and
![]() in the laminar viscous case,
remembering that
in the laminar viscous case,
remembering that
![]() in both cases and that
in both cases and that
![]() (see also Eq. (81)).
(see also Eq. (81)).
Figure 3 demonstrates furthermore that dust particles
moving with supersonic drift velocities cannot be expected in brown
dwarf atmospheres. Similarly, the turbulent flow regime with dust
Reynolds numbers
![]() is barely reached at
very large densities. Therefore, we can conclude that for dust grains in
brown dwarf atmospheres the subsonic free molecular flow and the
laminar viscous flow are the important cases to be investigated.
is barely reached at
very large densities. Therefore, we can conclude that for dust grains in
brown dwarf atmospheres the subsonic free molecular flow and the
laminar viscous flow are the important cases to be investigated.
Copyright ESO 2003