7 Conclusions

In this paper, we have investigated the basic physical and chemical processes which are responsible for the formation, the temporal evolution and the precipitation of dust grains in brown dwarf atmospheres.

In contrast to other astronomical sites of effective dust formation, the dust particles are embedded in such a dense gas that the Knudsen numbers may fall short of unity. This requires a careful fall differentiation for the different hydrodynamical regimes: free molecular flow (subsonic and supersonic) and slip flow (laminar and turbulent case).

Compiling a general formula for the drag force from the different special cases, we have shown that the large gravity in brown dwarf atmospheres forces the dust particles to move with a considerably high downward drift velocity relative to the gas. The acceleration of the dust particles (on a time-scale $\tau _{\rm acc}$) towards the equilibrium drift velocity (final fall speed) results to be always much faster than any other considered process (nucleation, growth, hydrodynamical acceleration and sedimentation) such that an instantaneous acceleration of the particles to equilibrium drift can be assumed. In contrast, the outward acceleration of dust grains due to radiation pressure is completely negligible in brown dwarf atmospheres.

The large drift velocities are found to limit the residence time of the forming dust grains and hence their maximum size  $a_{\rm max}$ as

$$a_{\rm max} \approx \left\{\begin{array}{rl} \!\!\!\left(\fr... ...t)\!\right)^{1/4} &\!\!, {Kn}\!\ll\!1 . \end{array}\right.$$ (81)

Typical values for $a_{\rm max}$ vary between $\approx$1 $\mu$m in the thin outermost atmospheric layers and $\approx$100 $\mu$m in the dense innermost layers. As soon as the particles come close to this limiting size, they rain out quickly. This maximum size does not allow for the existence of supersonic dust particles or dust particles with very high Reynolds numbers, such that the subsonic free molecular flow and the laminar viscous flow are the important main cases to be discussed for dust grains in brown dwarf atmospheres.

For small Knudsen numbers, the growth of the particles by accretion of molecules is limited by the diffusion of the molecules towards the grain surface, and the energy exchange with the surrounding gas is limited by heat conduction. The latter process co-works with the radiative gains and losses of the hot grains. According to our results, the release of latent heat during the growth does only lead to a small increase of the grain temperature ($<\!5~$K) and has no particular influence on the growth rates.

Based on these findings, we have formulated a system of partial differential equations for the consistent physical description of the dust component in brown dwarf and giant gas planet atmospheres. These moment equations represent an unique tool to model the nucleation, growth and size-dependent equilibrium drift of the dust particles, and the element depletion/enrichment of the gas. We consider such a description as essential, because these processes occur simultaneously and are strongly coupled. The description allows for an inclusion into hydrodynamics or classical stellar atmosphere calculations, although a few unsolved questions still remain, e.g.a reliable closure condition and a clean Knudsen number fall differentiation.

A dimensionless analysis of the moment equations reveals the existence of the following three regimes associated with the formation of a cloud layer:

1)

At high altitudes the temperatures are much lower than the sublimation temperatures of the various solid materials and the gas is highly supersaturated. Consequently, nucleation is effective and we find the following relation between the time-scales inherent in the different physical processes:

$$\tau_{\rm acc} ~\ll~ \tau_{\rm nuc} ~\la~ \tau_{\rm gr} ~\ll~ \tau_{\rm hyd} ~\ll~ \tau_{\rm sink} \quad\ (S \gg 1) .$$

This means that the dust particles are mainly created here (by nucleation) as consequence of hydrodynamical enrichment events, e.g. due to the mixing caused by the convection. The particles in this region of efficient nucleation remain much smaller than $a_{\rm max}$. The gravitational settling of the grains is very slow such that they form a rather passive component, subject to hydrodynamical streams (e.g.winds).

2)

At lower altitudes where the temperatures are close to the sublimation temperatures (the cloud layer is expected to reach its maximum opacity here), nucleation is inefficient and the particle growth is the leading physical process

$$\tau_{\rm acc} ~\ll~ \tau_{\rm gr} ~<~ \tau_{\rm hyd} ~\la~ \tau_{\rm sink} \quad\quad(S \ga 1) .$$

In this growth-dominated region, the dust particles may reach much larger sizes, only limited by element consumption or, eventually, by gravitational settling when they even reach $a_{\rm max}$. Anyway, the dust growth will be essentially completed before the particles are influenced by drift. The dust grains are not created here (by nucleation) but are transported into these layers by winds or rain in from above. The efficient growth will consume most of the condensable elements from these layers and thereby bring the supersaturation ratio close to unity in this region.

3)

Below the cloud base, the temperatures are higher than the sublimation temperatures, and the dust grains that rain in from above will quickly evaporate

$$\tau_{\rm acc} ~\ll~ \tau_{\rm evap} ~\approx~\tau_{\rm sink} ~\la~\tau_{\rm hyd} \quad\quad(S \la 1) ,$$

thereby releasing the condensable elements of the grains and enriching the surrounding gas.

It remains to be pointed out, however, that in a turbulent fluid field considerable variations of the thermodynamical conditions may occur. For example, the nucleation of dust particles may take place even in a dust-hostile environment, if interfering expansion waves temporarily cause low temperatures, i.e.high supersaturation ratios (Paper I). In such turbulent environments, the correlation between the supersaturation ratio S and the atmospheric height (as assumed in the upper item list) is loosened. Thus, the regimes are characterised by S rather than by the atmospheric height, and may possibly occur also on small scales.

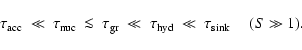
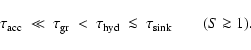
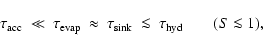
The life cycle of dust grains in brown dwarf atmospheres is finally completed by convective streams which mix up gas from the deep interior into the upper layers. On a large scale, we expect an intricate balance of this upward mixing of condensable elements by convection with the downward gravitational settling of the condensing dust grains, which will determine the large-scale structure of the element abundances in the atmosphere related to the observation of the various molecular features.

This work will be continued in the next paper of this series by solving the dust moment equations for the special case of a static atmosphere.

Acknowledgements

We thank T. Tsuji for contributing the hydrostatic reference model atmosphere and Akemi Tamanai for providing us with an electronic version of the optical constants of amorphous quartz. The anonymous referee is thanked for helpful comments, in particular concerning the fricional heating. We thank R. Klein for pointing out the work of Deufelhard ${\rm\hspace*{0.7ex}\&\hspace*{0.7ex}}$Wulkow. This work has been supported by the DFG (Sonderforschungsbereich 555, Teilprojekt B8, and grand Se 420/19-1 and 19-2). Most of the literature search has been performed with the ADS system.