

Up: Dust in brown dwarfs
4 Energy balance of dust grains
The surface chemical reactions responsible for the growth of a dust
particle liberate the latent heat of condensation
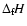 [erg/g] which
causes a heating of the grain as
[erg/g] which
causes a heating of the grain as
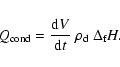 |
(39) |
It has been proposed (Cooper
 2002) that this heating can increase
the internal dust temperature
2002) that this heating can increase
the internal dust temperature 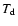 substantially, until the
sublimation temperature is reached (where
substantially, until the
sublimation temperature is reached (where  ). In that case,
the growth rate is limited by the need to remove the latent heat
of condensation from the grain and Eqs. (22) and
(32) are not valid.
). In that case,
the growth rate is limited by the need to remove the latent heat
of condensation from the grain and Eqs. (22) and
(32) are not valid.
A further heating process of the dust particle is given by the
friction caused by the motion relative to the gas,
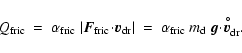 |
(40) |
Hereby, we assume that the total work done by the frictional force per
time,
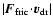 ,
is converted into heat, from
which the fraction
,
is converted into heat, from
which the fraction
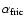 is delivered to the grain. For
the r.h.s. expression, the condition of equilibrium drift
is delivered to the grain. For
the r.h.s. expression, the condition of equilibrium drift
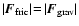 is used
(Eq. (5)). Since elastic collisions do not transfer any
energy, we assume
is used
(Eq. (5)). Since elastic collisions do not transfer any
energy, we assume
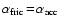 (see
Eq. (43))
(see
Eq. (43))![[*]](/icons/foot_motif.gif) .
.
In order to determine the dust temperature increase, we balance these heating
processes with the net energy losses due to radiation and due to inelastic
collisions. The net radiative cooling rate of a single dust grain is given by
![\begin{displaymath}Q_{\rm rad} = 4\pi\!\!\int\!\!\pi a^2 Q_{\rm abs}(a,\lambda) ...
...ig[B_{\lambda}(T_{\rm d})-J_{\lambda}\big] ~{\rm d}\lambda \ ,
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img288.gif) |
(41) |
where
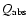 is the absorption efficiency,
is the absorption efficiency,
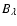 the Planck function
and
the Planck function
and
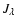 the mean intensity of the radiation field.
the mean intensity of the radiation field.
The cooling due to inelastic collisions with gas particles, in particular with
H2, depends again on the Knudsen number. For large Knudsen numbers (
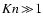 )
the collisional cooling rate is given by
)
the collisional cooling rate is given by
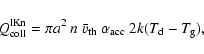 |
(42) |
where 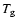 is the gas temperature,
is the gas temperature,
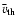 the mean thermal velocity introduced on page 300 and
the mean thermal velocity introduced on page 300 and
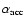 the efficiency for thermal accommodation,
given by Burke
the efficiency for thermal accommodation,
given by Burke
 Hollenbach (1983)
Hollenbach (1983)
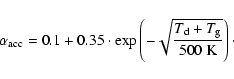 |
(43) |
For small Knudsen numbers (
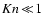 ), the removal
of heat from the grain's surface in the laminar
case
), the removal
of heat from the grain's surface in the laminar
case![[*]](/icons/foot_motif.gif) is limited by the heat
conductivity of the ambient gas. We consider the energy equation of an
ideal fluid
is limited by the heat
conductivity of the ambient gas. We consider the energy equation of an
ideal fluid
![\begin{displaymath}\frac{{\rm\partial} }{{\rm\partial} t}(\rho~e) + \nabla \big(\vec{v}_{\rm gas}[\rho~e+P]\big) = - \nabla \vec{j}_{\rm HC}
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img297.gif) |
(44) |
where e is the internal energy of the gas including kinetic and
gravitational potential energies (Paper I) and P the
thermal gas pressure. The energy flux by heat conduction is given by
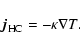 |
(45) |
![$\kappa\;\rm [erg~K^{-1}cm^{-1}s^{-1}]$](/articles/aa/full/2003/07/aah3912/img299.gif) is the heat conductivity
of the gas which according to Jeans (1967) equals
is the heat conductivity
of the gas which according to Jeans (1967) equals
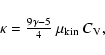 |
(46) |
where
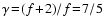 is the adiabatic index, f the
number of degrees of freedom,
is the adiabatic index, f the
number of degrees of freedom,
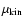 the kinematic viscosity
(Eq. (9)) and
the kinematic viscosity
(Eq. (9)) and
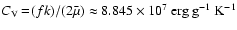 the isochoric heat capacity of the gas, resulting in
the isochoric heat capacity of the gas, resulting in
![\begin{displaymath}\kappa = 988~{\rm\frac{erg}{\rm K~cm~s}}~\sqrt{T_{\rm g}\rm [K]} .
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img303.gif) |
(47) |
The further derivation of the cooling rate by heat conduction is
analogous to the derivation of the viscous growth rate on
page 303. We consider the static case
(
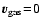 )
and assume stationary (
)
and assume stationary (
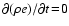 )
and spherical symmetry, such that
Eq. (44) becomes
)
and spherical symmetry, such that
Eq. (44) becomes
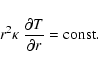 |
(48) |
Regarding 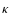 as a constant, the solution of
Eq. (48) with boundary conditions
as a constant, the solution of
Eq. (48) with boundary conditions
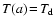 and
and
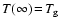 is
is
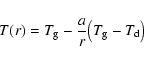 |
(49) |
and the collisional cooling rate
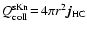 ,
according to Eqs. (45) and (49),
results in
,
according to Eqs. (45) and (49),
results in
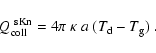 |
(50) |
The general collisional cooling rate with
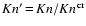 is
again approximated by
is
again approximated by
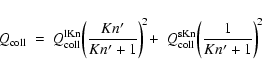 |
(51) |
where
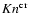 results from equating Eqs. (42)
with (50). We find a value of 0.023 at 1000 K
and a value of 0.019 at 2000 K. For simplicity, we apply a constant
value for the critical Knudsen number as
results from equating Eqs. (42)
with (50). We find a value of 0.023 at 1000 K
and a value of 0.019 at 2000 K. For simplicity, we apply a constant
value for the critical Knudsen number as
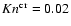 in
the following.
in
the following.
The energy balance of a single dust grain is finally given by
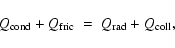 |
(52) |
which states an implicit equation for the temperature increase
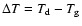 due to the liberation of latent heat during grain growth
and frictional heating.
due to the liberation of latent heat during grain growth
and frictional heating.
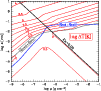 |
Figure 4:
Contour plot of the temperature increase
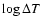 [K],
due to the liberation of latent heat during grain growth and
frictional heating, as function of the grain radius a and gas
density [K],
due to the liberation of latent heat during grain growth and
frictional heating, as function of the grain radius a and gas
density 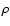 at constant gas temperature
at constant gas temperature
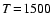 K for
quartz grains with the same parameters as in
Fig. 3. We assume growth by accretion of the key
species SiO with maximum particle density K for
quartz grains with the same parameters as in
Fig. 3. We assume growth by accretion of the key
species SiO with maximum particle density
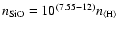 and extreme
supersaturation (
and extreme
supersaturation (
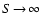 ). The two dashed lines indicate
where the two considered heating and cooling rates are equal.
Above these lines, ). The two dashed lines indicate
where the two considered heating and cooling rates are equal.
Above these lines,
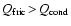 and
and
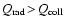 ,
respectively. ,
respectively. |
Figure 4 shows an example for the resulting temperature
increase 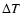 of quartz grains. We assume
of quartz grains. We assume
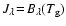 and again consider the explicit
growth reaction (Eq. (38)) with a release of latent
heat of
and again consider the explicit
growth reaction (Eq. (38)) with a release of latent
heat of
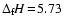 eV per reaction at 1000 K, 5.61 eV at
1500 K and 5.49 eV at 2000 K (data reduced from the
enthalpies of formation of the involved molecules and the solid,
source: JANAF-tables, electronic version, Chase
eV per reaction at 1000 K, 5.61 eV at
1500 K and 5.49 eV at 2000 K (data reduced from the
enthalpies of formation of the involved molecules and the solid,
source: JANAF-tables, electronic version, Chase
 1985).
1985).
For the sake of simplicity, we furthermore assume
 |
(53) |
for this calculation, where the extinction efficiency over a in the
small particle limit of Mie theory is given by
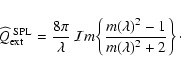 |
(54) |
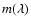 is the complex refractory index of the dust
grain material and
is the complex refractory index of the dust
grain material and 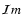 the imaginary part. The optical
constants for amorphous SiO2 (quartz glass) are taken from
H. R. Philipp's section in (Palik 1985) and the
resulting
the imaginary part. The optical
constants for amorphous SiO2 (quartz glass) are taken from
H. R. Philipp's section in (Palik 1985) and the
resulting
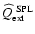 -values are
log-log-interpolated between the measured wavelengths points.
-values are
log-log-interpolated between the measured wavelengths points.
Despite these simplifications, Fig. 4 clearly indicates
that the warming of the dust grains due to the release of latent heat
is negligible, being less than 3.5 K all over the relevant parts of
the size-density-plane, where
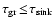 (compare Fig. 3). Here, we find that this heating is
balanced by collisional cooling
(compare Fig. 3). Here, we find that this heating is
balanced by collisional cooling
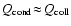 .
Since both heating/cooling rates scale as
.
Since both heating/cooling rates scale as
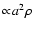 for large
Knudsen numbers and as
for large
Knudsen numbers and as
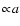 for small Knudsen numbers, a
constant value for
for small Knudsen numbers, a
constant value for 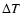 tunes in for both cases,
tunes in for both cases,
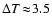 K for large Kn, and
K for large Kn, and
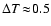 K for
small Kn. Note that the calculated temperature differences are always
an upper estimate. The actual temperature differences may be much
smaller because we have assumed solar, undepleted abundances of Si in
the gas phase and
K for
small Kn. Note that the calculated temperature differences are always
an upper estimate. The actual temperature differences may be much
smaller because we have assumed solar, undepleted abundances of Si in
the gas phase and
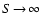 for the calculation of
for the calculation of
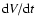 .
.
For larger particles (roughly at
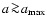 as defined in
Sect. 3.1), the character of the energy balance of the dust
particles changes. Here, the frictional heating due to the rapid
relative motion and the radiative cooling dominate, i.e.
as defined in
Sect. 3.1), the character of the energy balance of the dust
particles changes. Here, the frictional heating due to the rapid
relative motion and the radiative cooling dominate, i.e.
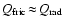 .
Much larger temperature deviations up
to 10 000 K result in this case. However, as argued before, such
large grains cannot be formed in brown dwarf atmospheres.
.
Much larger temperature deviations up
to 10 000 K result in this case. However, as argued before, such
large grains cannot be formed in brown dwarf atmospheres.
Thus, the resulting increase of the dust temperature 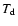 is by far
too small to reach the sublimation temperature
is by far
too small to reach the sublimation temperature
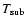 ,
unless
gas temperatures very close to
,
unless
gas temperatures very close to
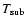 are considered and,
therefore, Eqs. (22) and (32) remain
valid.
are considered and,
therefore, Eqs. (22) and (32) remain
valid.


Up: Dust in brown dwarfs
Copyright ESO 2003
![]() [erg/g] which
causes a heating of the grain as
[erg/g] which
causes a heating of the grain as
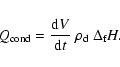
![]() )
the collisional cooling rate is given by
)
the collisional cooling rate is given by
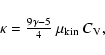

![]() of quartz grains. We assume
of quartz grains. We assume
![]() and again consider the explicit
growth reaction (Eq. (38)) with a release of latent
heat of
and again consider the explicit
growth reaction (Eq. (38)) with a release of latent
heat of
![]() eV per reaction at 1000 K, 5.61 eV at
1500 K and 5.49 eV at 2000 K (data reduced from the
enthalpies of formation of the involved molecules and the solid,
source: JANAF-tables, electronic version, Chase
eV per reaction at 1000 K, 5.61 eV at
1500 K and 5.49 eV at 2000 K (data reduced from the
enthalpies of formation of the involved molecules and the solid,
source: JANAF-tables, electronic version, Chase
![]() 1985).
1985).

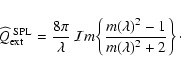
![]() (compare Fig. 3). Here, we find that this heating is
balanced by collisional cooling
(compare Fig. 3). Here, we find that this heating is
balanced by collisional cooling
![]() .
Since both heating/cooling rates scale as
.
Since both heating/cooling rates scale as
![]() for large
Knudsen numbers and as
for large
Knudsen numbers and as
![]() for small Knudsen numbers, a
constant value for
for small Knudsen numbers, a
constant value for ![]() tunes in for both cases,
tunes in for both cases,
![]() K for large Kn, and
K for large Kn, and
![]() K for
small Kn. Note that the calculated temperature differences are always
an upper estimate. The actual temperature differences may be much
smaller because we have assumed solar, undepleted abundances of Si in
the gas phase and
K for
small Kn. Note that the calculated temperature differences are always
an upper estimate. The actual temperature differences may be much
smaller because we have assumed solar, undepleted abundances of Si in
the gas phase and
![]() for the calculation of
for the calculation of
![]() .
.
![]() as defined in
Sect. 3.1), the character of the energy balance of the dust
particles changes. Here, the frictional heating due to the rapid
relative motion and the radiative cooling dominate, i.e.
as defined in
Sect. 3.1), the character of the energy balance of the dust
particles changes. Here, the frictional heating due to the rapid
relative motion and the radiative cooling dominate, i.e.
![]() .
Much larger temperature deviations up
to 10 000 K result in this case. However, as argued before, such
large grains cannot be formed in brown dwarf atmospheres.
.
Much larger temperature deviations up
to 10 000 K result in this case. However, as argued before, such
large grains cannot be formed in brown dwarf atmospheres.
![]() is by far
too small to reach the sublimation temperature
is by far
too small to reach the sublimation temperature
![]() ,
unless
gas temperatures very close to
,
unless
gas temperatures very close to
![]() are considered and,
therefore, Eqs. (22) and (32) remain
valid.
are considered and,
therefore, Eqs. (22) and (32) remain
valid.