The trajectory
![]() of a spherical dust particle of radius a and
mass
of a spherical dust particle of radius a and
mass
![]() ,
floating in a gaseous
environment like a stellar atmosphere, is determined by Newton's law
,
floating in a gaseous
environment like a stellar atmosphere, is determined by Newton's law
The gravitational force on the grain is given by
The radiative force is given by the momentum transfer from the ambient
radiation field to the grain due to absorption and scattering of photons
However, as the following rough estimation will demonstrate, the radiative
force is small compared to the other forces in brown dwarf atmospheres and can
be neglected. We simplify the integral in Eq. (3) by pulling out
the flux mean extinction efficiency
![]() .
The
wavelength integrated Eddington flux is given by
.
The
wavelength integrated Eddington flux is given by
![]() ,
where
,
where
![]() is the Stefan-Boltzmann constant and
is the Stefan-Boltzmann constant and
![]() is the effective
temperature of the star. Considering furthermore the small particle limit
(SPL) of Mie theory
is the effective
temperature of the star. Considering furthermore the small particle limit
(SPL) of Mie theory
![]() (Rayleigh limit), the extinction
efficiency is proportional to the grain size
(Rayleigh limit), the extinction
efficiency is proportional to the grain size
![]() ,
and Eq. (3) results in
,
and Eq. (3) results in
|
|
|
|
| Red Giant: | ||
|
|
||
| 101 |
|
|
| 104 |
|
|
| Brown Dwarf: | ||
|
|
||
| 101 |
|
|
| 104 |
|
|
Table 1 demonstrates that the radiative force on dust
grains in brown dwarf atmospheres is always much smaller than the
gravity, even in case of light but opaque grains![]() . Consequently, the radiative force can be
neglected, and the dust grain's equation of motion
(Eq. (1)) simplifies to
. Consequently, the radiative force can be
neglected, and the dust grain's equation of motion
(Eq. (1)) simplifies to
An unique description of the frictional force (drag force) is difficult to obtain for brown dwarf atmospheres. These difficulties arise from the fact that the behaviour of the gas flow around the moving dust grain changes qualitatively with changing grain size, changing drift velocity and/or changing thermodynamic state of the gas. There are transitions from freely impinging gas particles to a viscous flow, from a subsonic to a supersonic behaviour, and from a laminar flow to turbulence. The physical conditions in brown dwarf atmospheres are such that all transitions may possibly occur. Reliable physical descriptions of the drag force are only available in certain limited regimes and an unique description must be compiled from these special cases.
In order to quantify the behaviour of the streaming gas flow, the
following characteristic numbers are introduced: the Knudsen number Kn and
the dust Reynolds number
![]() .
The Knudsen number Kn is
defined by the ratio of the mean free path length of the gas particles
.
The Knudsen number Kn is
defined by the ratio of the mean free path length of the gas particles
![]() to a typical dimension
to a typical dimension
![]() of the gas flow
under consideration, here given by the diameter of the grain
of the gas flow
under consideration, here given by the diameter of the grain
In contrast, if
![]() ,
inter-molecular collisions are
frequent and the stream of gas particles colliding with the dust grain
becomes viscous. In this case, the drag force cannot be obtained via
reduction to elementary collisions. This is the regime of continuum
theory for which well-tested empirical formulae are available, e.g.
from engineering science (viscous case or slip flow), depending
on whether the gas flow around the dust grain is laminar or turbulent.
In order to characterise the transition from laminar (Stokes) friction
to turbulent (Newtonian) friction, the dust grain's Reynolds number
,
inter-molecular collisions are
frequent and the stream of gas particles colliding with the dust grain
becomes viscous. In this case, the drag force cannot be obtained via
reduction to elementary collisions. This is the regime of continuum
theory for which well-tested empirical formulae are available, e.g.
from engineering science (viscous case or slip flow), depending
on whether the gas flow around the dust grain is laminar or turbulent.
In order to characterise the transition from laminar (Stokes) friction
to turbulent (Newtonian) friction, the dust grain's Reynolds number
![]() is introduced
is introduced
In order to evaluate the kinematic viscosity of the gas
![]() we follow the considerations of Jeans
(1967) for a mixture of ideal gases
we follow the considerations of Jeans
(1967) for a mixture of ideal gases
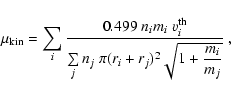 |
(8) |
Considering the mechanics of rarefied gases, Schaaf (1963)
derives a formula for the drag force by freely impinging gas particles due to
elastic collisions, equally applicable in the subsonic as well as in the
supersonic range,
In this regime, continuum theory is valid for which well-tested
empirical formulae exist. Lain
![]() (1999), carrying out
experimental studies on bubbly flows, arrive at the following
empirical expression for the drag force
(1999), carrying out
experimental studies on bubbly flows, arrive at the following
empirical expression for the drag force
Using Eq. (7), the drag force in the viscous case according to
Eq. (14) is found to have the following
asymptotic behaviour
For flows with an intermediate Knudsen number (
![]() ), so-called transitions flows, reliable expressions
for the drag force are difficult to obtain. We therefore define a
critical Knudsen number
), so-called transitions flows, reliable expressions
for the drag force are difficult to obtain. We therefore define a
critical Knudsen number
![]() where
where
![]() equals
equals
![]() .
Considering the limiting cases of subsonic drift velocities and small
.
Considering the limiting cases of subsonic drift velocities and small
![]() in Eqs. (13) and (16),
respectively, the result is exactly
in Eqs. (13) and (16),
respectively, the result is exactly
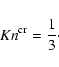 |
(17) |
Considering a dust particle of constant radius a floating in a gas at
constant thermodynamical conditions (![]() ,
T) and a constant
velocity
,
T) and a constant
velocity
![]() ,
the particle will be accelerated until a
force equilibrium is reached, where the gravitational acceleration is
balanced by frictional deceleration
,
the particle will be accelerated until a
force equilibrium is reached, where the gravitational acceleration is
balanced by frictional deceleration
Figure 1 shows the resulting values of
![]() in a brown
dwarf's atmosphere with
in a brown
dwarf's atmosphere with
![]() .
The equilibrium drift velocities
roughly range in
[10-4,10+6] cm s-1 and are generally smaller
for small particles and large densities. The small bendings of the contour
lines around
.
The equilibrium drift velocities
roughly range in
[10-4,10+6] cm s-1 and are generally smaller
for small particles and large densities. The small bendings of the contour
lines around
![]() are no numerical artifacts but result
from the measured re-increase of the drag coefficient of spherical particles
are no numerical artifacts but result
from the measured re-increase of the drag coefficient of spherical particles
![]() between
between
![]() and
and
![]() (Eq. (15)), associated with the transition from laminar to
turbulent friction.
(Eq. (15)), associated with the transition from laminar to
turbulent friction.
Small dust particles can sustain longer in the respective atmospheric
layers, whereas large grains will "rain out'' sooner. Only dust
particles ![]() 100
100 ![]() m at gas densities
m at gas densities ![]() 10
10
![]() can hereby reach a drift velocity beyond the local
velocity of sound
can hereby reach a drift velocity beyond the local
velocity of sound
![]() .
However, such particles will remove themselves so
quickly from the respective atmospheric layers (
.
However, such particles will remove themselves so
quickly from the respective atmospheric layers (
![]() s) that this case seems very unlikely to be relevant
for any part of the atmosphere, unless there exists a physical process
(convective streams or atmospheric winds) which is capable to produce
supersonic upwinds. The time-scale for gravitational
settling is hereby defined as
s) that this case seems very unlikely to be relevant
for any part of the atmosphere, unless there exists a physical process
(convective streams or atmospheric winds) which is capable to produce
supersonic upwinds. The time-scale for gravitational
settling is hereby defined as
Figure 1 demonstrates furthermore that even the
smallest dust particles cannot sustain forever but will slowly sink
into deeper layers. Assuming that the dust particles do not grow
along their way down the atmosphere (which would increase their drift
velocity), a ![]() m-particle starting in an atmospheric layer
with
m-particle starting in an atmospheric layer
with
![]() g cm-3 needs about
g cm-3 needs about
![]() s (8 months) to pass one
scale height. A dust particle with
s (8 months) to pass one
scale height. A dust particle with
![]() m needs only
m needs only
![]() 1/4 hour
1/4 hour![]() .
.
The destiny of those particles drifting inward is to finally reach an
atmospheric layer where the temperature is high enough to evaporate
them thermally. This sets free the elements the dust grains are
composed off and thereby enriches the surrounding gas in this
layer. Hence, the rain-out will tend to saturate the gas below the
cloud base, where the "cloud base'' is identified with the level in
the atmosphere where the dust grains are just thermodynamically stable
(![]() ,
see Sect. 3).
,
see Sect. 3).
The actual relative velocity of the dust particle with respect to the
gas,
![]() ,
can of course deviate from its equilibrium value
defined in Sect. 2.4. It will only asymptotically reach
,
can of course deviate from its equilibrium value
defined in Sect. 2.4. It will only asymptotically reach
![]() for
for
![]() ,
if the parameters a,
,
if the parameters a,
![]() ,
,
![]() and T are constant. However, considering a dust particle
created in a brown dwarf atmosphere, the particle may grow by
accretion of molecules (
and T are constant. However, considering a dust particle
created in a brown dwarf atmosphere, the particle may grow by
accretion of molecules (
![]() ,
see Sect. 3)
and the physical state of the surrounding gas may change with time
(e.g.
,
see Sect. 3)
and the physical state of the surrounding gas may change with time
(e.g.
![]() )
as the particle sinks into deeper layers of
the atmosphere. Turbulence may furthermore create a time-dependent
velocity field (
)
as the particle sinks into deeper layers of
the atmosphere. Turbulence may furthermore create a time-dependent
velocity field (
![]() ), which provides an additional
cause for temporal deviations between
), which provides an additional
cause for temporal deviations between
![]() and
and
![]() .
.
Thus, an important question for the discussion of the dynamical
behaviour of the dust component in brown dwarf atmosphere is, whether
or not
![]() can be replaced by
can be replaced by
![]() ,
at least
approximately.
,
at least
approximately.
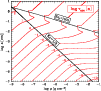 |
Figure 2:
Contour plot of the acceleration time-scale towards equilibrium
drift
|
In order to discuss this question, we consider the dust particle
acceleration time-scale
![]() towards equilibrium drift. Expressing
the dust particle's equation of motion (Eq. (5)) in terms
of the first-order differential equation
towards equilibrium drift. Expressing
the dust particle's equation of motion (Eq. (5)) in terms
of the first-order differential equation
![]() with
with
![]() and
and
![]() ,
and
assuming small deviations
,
and
assuming small deviations ![]() from the stability point
from the stability point
![]() (where
(where
![]() ), the temporal change of y is
), the temporal change of y is
![]() .
Accordingly, the acceleration time-scale is given by
.
Accordingly, the acceleration time-scale is given by
![]() ,
or
,
or
For a powerlaw dependence
![]() ,
Eqs. (20) and (21) result in
,
Eqs. (20) and (21) result in
![]() ,
i.e.we find
,
i.e.we find
![]() for
for
![]() .
Since
Sect. 3 will demonstrate that also the growth of the
dust particles is slow in comparison to
.
Since
Sect. 3 will demonstrate that also the growth of the
dust particles is slow in comparison to
![]() ,
we may conclude that
the concept of equilibrium drift provides a good approximation for the
description of the size-dependent relative velocities between dust and
gas in brown dwarf atmospheres.
,
we may conclude that
the concept of equilibrium drift provides a good approximation for the
description of the size-dependent relative velocities between dust and
gas in brown dwarf atmospheres.
Copyright ESO 2003