

Up: The non-thermal Sunyaev-Zel'dovich effect
Subsections
For galaxy clusters which contain two (or more) different electronic
populations, like radio-halo clusters which contain a thermal population
emitting X-rays and a non-thermal population producing the radio halo emission,
one has to evaluate the spectral distortion produced simultaneously by both
populations on the CMB radiation. Such a derivation has been not done so far. We
assume here that the two populations are independent and that no change on the
thermal population is induced by the non-thermal electrons. This condition is
reasonable for non-thermal electrons with energies
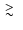 150 MeV which do
not appreciably loose energy through Coulomb collisions in the ICM (see, e.g.,
Blasi & Colafrancesco 1999; Colafrancesco & Mele 2001) and hence do not
produce a substantial heating of the IC gas. Electrons with
150 MeV which do
not appreciably loose energy through Coulomb collisions in the ICM (see, e.g.,
Blasi & Colafrancesco 1999; Colafrancesco & Mele 2001) and hence do not
produce a substantial heating of the IC gas. Electrons with
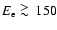 MeV
loose energy mainly through ICS and synchrotron losses. The radio halo emission
in galaxy clusters is, in fact, produced by electrons with energy
MeV
loose energy mainly through ICS and synchrotron losses. The radio halo emission
in galaxy clusters is, in fact, produced by electrons with energy
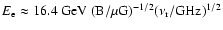 (see, e.g., Colafrancesco
& Mele 2001) which yield
(see, e.g., Colafrancesco
& Mele 2001) which yield
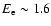 -52 GeV for a typical IC magnetic
field at the level of
-52 GeV for a typical IC magnetic
field at the level of 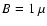 G at the typical frequencies,
G at the typical frequencies,
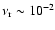 -10 GHz, at which radio halo spectra are observed. For such energies
the non-thermal electrons do not strongly affect the thermal IC gas. However, we
discuss in the following the impact of different non-thermal population spectra
on both the total SZ effect and on the cluster IC gas.
-10 GHz, at which radio halo spectra are observed. For such energies
the non-thermal electrons do not strongly affect the thermal IC gas. However, we
discuss in the following the impact of different non-thermal population spectra
on both the total SZ effect and on the cluster IC gas.
Under the hypothesis of independence between the thermal and non-thermal
electron populations, the probability that a CMB photon is scattered by an
electron of population A (say thermal) is not affected by the fact that the same
photon has been scattered by an electron of population B (say non-thermal).
Thus, at first order in  we expect that the total SZ effect is given by
the sum of the first order SZ effects due to each single population.
At higher order approximation in
we expect that the total SZ effect is given by
the sum of the first order SZ effects due to each single population.
At higher order approximation in  ,
however, one has to consider the effect
of repeated scattering (see Sect.2). It is intuitive to think that in this last
case the total SZ effect is not simply given by the sum of the separate SZ
effects at higher orders in
,
however, one has to consider the effect
of repeated scattering (see Sect.2). It is intuitive to think that in this last
case the total SZ effect is not simply given by the sum of the separate SZ
effects at higher orders in  and the terms describing the
cross-scattering between CMB photons and the electrons of populations A and B
have to be taken into account. In the following, we will derive in detail the
general expression for the total SZ distortion caused by a combination of two
electronic populations.
and the terms describing the
cross-scattering between CMB photons and the electrons of populations A and B
have to be taken into account. In the following, we will derive in detail the
general expression for the total SZ distortion caused by a combination of two
electronic populations.
Let us consider two electron populations with momentum distributions
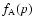 and
and
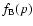 with optical depths
with optical depths
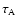 and
and
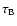 ,
respectively. We also
assume that the two electron distributions are both normalized to 1. The total
distribution of the electron momenta is
,
respectively. We also
assume that the two electron distributions are both normalized to 1. The total
distribution of the electron momenta is
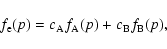 |
(52) |
with appropriate normalization coefficients 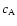 and
and 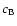 .
Since the total
distribution
.
Since the total
distribution
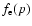 is also normalized to 1, the coefficients
is also normalized to 1, the coefficients 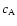 and
and 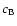 are related by the condition
are related by the condition
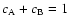 .
The coefficients
.
The coefficients 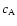 and
and 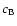 yield
the weight of each population with respect to the other and thus their ratio is
given by
yield
the weight of each population with respect to the other and thus their ratio is
given by
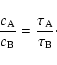 |
(53) |
Such a condition, together with the normalization condition, yields:
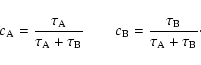 |
(54) |
The total distribution
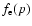 has an optical depth given by
has an optical depth given by
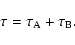 |
(55) |
In fact, the probability that a CMB photon can suffer n scatterings by the
electrons of each distribution is given by the sum of all the possible
combinations of the probability to suffer 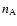 scatterings from the electrons
of the distribution
scatterings from the electrons
of the distribution 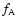 and the probability to suffer
and the probability to suffer 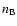 scattering from
the electrons of the distribution
scattering from
the electrons of the distribution 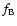 ,
with
,
with
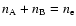 .
Since the two
distributions are independent, this probability is given by the product of the
two separate probabilities:
.
Since the two
distributions are independent, this probability is given by the product of the
two separate probabilities:
(we assume here a Poisson probability distribution). This means that the electrons of the distribution 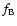 simply add to the electrons of the distribution
simply add to the electrons of the distribution 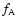 .
In fact, from the definition of optical depth, one gets:
.
In fact, from the definition of optical depth, one gets:
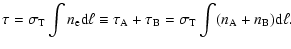 |
|
|
(57) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{distorslp2.eps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg284.gif) |
Figure 14:
The spectral distortion in units of
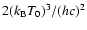 for a non-thermal population given by Eq. (34) computed for p1= 0.5 (solid), 1 (dashes), 10 (dotted) and 100 (dot-dashes).
for a non-thermal population given by Eq. (34) computed for p1= 0.5 (solid), 1 (dashes), 10 (dotted) and 100 (dot-dashes). |
The exact expression for the spectral distortion produced by two electron populations can be evaluated from Eqs. (19)-(21), using the appropriate expression for P1(s).
The general expression for the distribution P1(s) is given by:
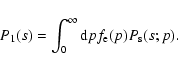 |
(58) |
Inserting Eq. (52) in Eq. (58) one obtains the function P1(s)for two populations as a function of the distributions P1(s) of each single
population:
The Fourier transform of Eq. (59) is
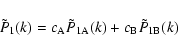 |
(60) |
and from this expression one obtains the Fourier transform of the total redistribution
function:
The exact total redistribution function
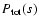 is given by the
convolution of the redistribution functions of the separate electron
populations:
is given by the
convolution of the redistribution functions of the separate electron
populations:
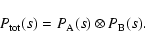 |
(62) |
Thus, the exact spectral distortion produced by two electron populations on the
CMB radiation is given by:
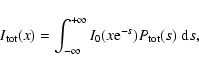 |
(63) |
in terms of the exact total redistribution function
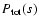 given in Eq. (62). We
also give in the Appendix the analytic expressions for the approximations at
first and second order in
given in Eq. (62). We
also give in the Appendix the analytic expressions for the approximations at
first and second order in  of the total spectral distortion
of the total spectral distortion
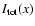 .
.
4.1 The function
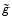 (x) for a combination of two electron populations
(x) for a combination of two electron populations
The total SZ effect produced by the combination of two electron populations can
be written again in terms of a Comptonization parameter
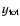 and of a
spectral function
and of a
spectral function
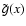 ,
in the form of Eq. (22). For two electron
populations, we can write the average temperature in Eq. (46) as:
,
in the form of Eq. (22). For two electron
populations, we can write the average temperature in Eq. (46) as:
The Comptonization parameter
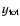 can be evaluated using
Eq. (49) as:
can be evaluated using
Eq. (49) as:
At first order in  ,
the function
,
the function
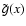 for two populations can be expressed as
for two populations can be expressed as
in terms of the functions
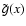 for each single electron population.
We notice that in this case the function
for each single electron population.
We notice that in this case the function
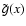 depends from the
Comptonization parameters, and hence from the optical depths, of the two
electron populations even at the first order approximation in
depends from the
Comptonization parameters, and hence from the optical depths, of the two
electron populations even at the first order approximation in  .
Moreover,
at higher orders in
.
Moreover,
at higher orders in  ,
the function
,
the function
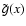 cannot be expressed
simply in terms of the spectral functions of the single populations because in
the expression for
cannot be expressed
simply in terms of the spectral functions of the single populations because in
the expression for
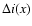 (see Eq. (A.10)), cross-correlation
terms appear.
(see Eq. (A.10)), cross-correlation
terms appear.
4.2 The SZ effect produced by a combination of a thermal plus a
non-thermal populations
Here we apply the previous derivation of the total SZ effect to a galaxy cluster
which contains both a termal and a non-thermal electron populations. In the
following computation of the total SZ effect for a Coma-like cluster we choose a
thermal population with the following parameters:
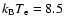 keV,
keV,
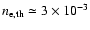 cm-3 and a cluster radius of
1
h50-1 Mpc. With these parameters the optical depth of the thermal
population is
cm-3 and a cluster radius of
1
h50-1 Mpc. With these parameters the optical depth of the thermal
population is
![\begin{displaymath}\tau_{\rm th}\simeq 6\times 10^{-3}
\left[\frac{n_{\rm e,th}}...
...3}}\right] \left[
\frac{\ell}{1~h_{50}^{-1}~{\rm Mpc}}\right],
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img310.gif) |
(67) |
and its pressure is:
![\begin{displaymath}P_{\rm th}\simeq 2.55\times10^{-2} ~{\rm keV ~cm}^{-3} \left[...
... \left[
\frac{k_{\rm B} T_{\rm e}}{8.5~ {\rm keV}}\right]\cdot
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img311.gif) |
(68) |
As for the spectrum of the non-thermal population we consider both the
phenomenological cases of a single and double power-law populations (see
Eq. (32) and Eq. (34) respectively). The parameters we
consider are specifically:
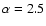 and
and
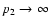 for the
single power-law population and
for the
single power-law population and
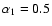 ,
,
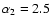 ,
with
,
with
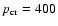 and
and
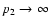 for the double power-law population. We
consider p1 as a free parameter in both cases. The relativistic electron
density has been normalized at
for the double power-law population. We
consider p1 as a free parameter in both cases. The relativistic electron
density has been normalized at
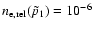 cm-3 for
cm-3 for
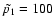 in both cases. The final SZ effect can be re-scaled simply to
different values of
in both cases. The final SZ effect can be re-scaled simply to
different values of
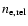 as discussed in Sect. 3.
as discussed in Sect. 3.
The amplitude of the non-thermal contribution to the total SZ effect increases with decreasing value of
p1. For the case of a single non-thermal power-law population it becomes
appreciable for
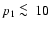 while for
while for
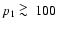 the total SZ effect
is indistinguishable from the pure thermal effect. In fact, for
the total SZ effect
is indistinguishable from the pure thermal effect. In fact, for
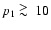 the function P1(s) is nearly coincident with that of a single thermal
population as shown in Fig. 15, while for p1 <10 the
function P1(s) is more a-symmetric towards large and positive values of s.
The peaks of the non-thermal distributions at large s are present in the total
distribution P1(s) but their amplitude decreases with
the function P1(s) is nearly coincident with that of a single thermal
population as shown in Fig. 15, while for p1 <10 the
function P1(s) is more a-symmetric towards large and positive values of s.
The peaks of the non-thermal distributions at large s are present in the total
distribution P1(s) but their amplitude decreases with
 and becomes lower and lower with increasing values of p1.
and becomes lower and lower with increasing values of p1.
![\begin{figure}
\par\includegraphics[width=8cm,height=5.43cm,clip]{prob1sa-tlp1.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg316.gif) |
Figure 15:
The function P1(s) (see Eq. (59)) for a combination
of thermal population and non-thermal population as in Eq. (32) with
p1= 0.5 (solid), 1 (dashes) and 10 (dotted). |
The amplitude and the shape of the total SZ effect in a cluster which contains
non-thermal phenomena depends on the spectral and spatial distribution of the
non-thermal population, given that the cluster IC gas properties are well known
from X-ray observations. We can take advantage of this fact to use the
non-thermal SZ effect as a tool to constrain the physical properties of the
non-thermal population. We show in Fig. 16 the total spectral distortion due to
the SZ effect in a cluster with non-thermal population as a function of p1.
Low values of
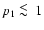 for the non-thermal population induce large
distortions with respect to the pure thermal SZ effect. However, for low values
of p1 the pressure of the non-thermal population with single power-law
distribution exceeds substantially the thermal pressure
for the non-thermal population induce large
distortions with respect to the pure thermal SZ effect. However, for low values
of p1 the pressure of the non-thermal population with single power-law
distribution exceeds substantially the thermal pressure
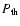 (see Table 7); as a consequence, the low energy electrons produce an
exceedingly large pressure unbalance and also a large heating of the IC gas,
which are not acceptable.
(see Table 7); as a consequence, the low energy electrons produce an
exceedingly large pressure unbalance and also a large heating of the IC gas,
which are not acceptable.
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,height=5.96cm,clip]{distorsa...
...includegraphics[width=7cm,height=5.96cm,clip]{distorsb-tlp1.eps} }
\end{figure}](/articles/aa/full/2003/01/aah3710/Timg318.gif) |
Figure 16:
The spectral distortion,
in units of
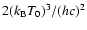 ,
of a single thermal population of a
Coma-like cluster (solid) is compared with the spectral distortion evaluated at first order in ,
of a single thermal population of a
Coma-like cluster (solid) is compared with the spectral distortion evaluated at first order in
 (see Eq. (A.6)), produced by a combination of thermal and
non-thermal population given in Eq. (32) with p1= 0.5 (dashes) and 1
(dotted) (left panel) and for
p1=10 (dashes), 100 (dotted) and 1000 (dot-dashes) (right panel).
(see Eq. (A.6)), produced by a combination of thermal and
non-thermal population given in Eq. (32) with p1= 0.5 (dashes) and 1
(dotted) (left panel) and for
p1=10 (dashes), 100 (dotted) and 1000 (dot-dashes) (right panel).
|
Table 7:
Values of pressure and density ratios
for a combination of thermal population and a non-thermal
population with single power-law spectrum
for different values of p1 (see text for details).
| p1 |
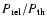 |
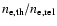 |
| 0.5 |
23.3 |
1.06 |
| 1 |
18.6 |
3.00 |
| 10 |
6.33 |
94.87 |
| 100 |
2.00 |
3000 |
| 1000 |
0.63 |
94868 |
The frequency location of the zero of the total SZ effect, x0, is also a
powerful diagnostic of the presence and of the nature of the non-thermal
population. The frequency location of x0 increases for decreasing values of
p1 as the impact of the non-thermal population becomes larger (see
Fig. 17). Consistently, x0 increases with increasing values
of the pressure ratio
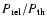 ,
as also shown in
Fig. 17.
,
as also shown in
Fig. 17.
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,height=5.97cm,clip]{zeri_2po...
...graphics[width=7cm,height=5.97cm,clip]{zeri_2pop_press_tlp1b.ps} }
\end{figure}](/articles/aa/full/2003/01/aah3710/Timg320.gif) |
Figure 17:
The behaviour of the zero of the total SZ effect evaluated
for a combination of thermal and non-thermal
population given by Eq. (32) is shown as a function of minimum momentum,
p1, of the non-thermal population
(left) and of the pressure ratio
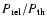 (right).
(right). |
In the case of a double power-law non-thermal population the ratio
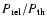 always remains of order 10-2 even for vary low values
always remains of order 10-2 even for vary low values
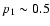 (see Table 8), and in this case there is a
negligible dynamical and thermal influence of the non-thermal population on the
thermal one.
(see Table 8), and in this case there is a
negligible dynamical and thermal influence of the non-thermal population on the
thermal one.
![\begin{figure}
\par\includegraphics[width=8.8cm,height=5.72cm,clip]{distors-tlp2...
...\includegraphics[width=8.8cm,height=5.72cm,clip]{distors-tlp2-c.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg321.gif) |
Figure 18:
The spectral distortion,
in units of
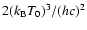 ,
of a single thermal population
(solid) is compared with the spectral distortion evaluated at first
order in ,
of a single thermal population
(solid) is compared with the spectral distortion evaluated at first
order in  produced by a combination of thermal and
non-thermal population given in Eq. (34) with
produced by a combination of thermal and
non-thermal population given in Eq. (34) with
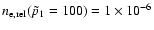 and p1= 0.5 (dashes), 1 (dotted), 10 (dot-dashes) and 100
(long dashes). We show the enlargement in the regions of the
minimum (top), of the zero (mid) and of the maximum
(bottom) of the total SZ effect.
and p1= 0.5 (dashes), 1 (dotted), 10 (dot-dashes) and 100
(long dashes). We show the enlargement in the regions of the
minimum (top), of the zero (mid) and of the maximum
(bottom) of the total SZ effect. |
In this case, also the total distribution P1(s) and the total spectral
distortion are little affected by the value of p1. We show in
Fig. 18 the spectral distortion of a single thermal
population compared with the spectral distortion produced by a combination of
thermal and non-thermal population with double power-law spectrum.
The contribution of the non-thermal population to the total SZ effect depends on
the normalization of the density
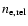 (which is highly uncertain). For increasing values of the
density of the non-thermal population the
non-thermal SZ effect becomes more relevant and produces substantial changes to
the SZ distortion produced by a single thermal population at frequencies
(which is highly uncertain). For increasing values of the
density of the non-thermal population the
non-thermal SZ effect becomes more relevant and produces substantial changes to
the SZ distortion produced by a single thermal population at frequencies
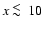 (see Fig. 19).
Much milder changes are present
in the high frequency range
(see Fig. 19).
Much milder changes are present
in the high frequency range
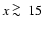 due to the low amplitude of the
non-thermal signal in this region (see, e.g., Fig. 14).
due to the low amplitude of the
non-thermal signal in this region (see, e.g., Fig. 14).
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm,clip]{dist-bc-tlp2.eps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg330.gif) |
Figure 19:
The spectral distortion,
in units of
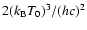 ,
of a single thermal population
(solid) is compared with the spectral distortion evaluated at first order in ,
of a single thermal population
(solid) is compared with the spectral distortion evaluated at first order in  produced by a combination of thermal and
non-thermal population given in Eq. (34) with p1= 0.5 and
produced by a combination of thermal and
non-thermal population given in Eq. (34) with p1= 0.5 and
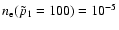 (dashes) and
(dashes) and
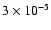 cm-3 (dotted). cm-3 (dotted). |
We also show in Fig. 20 the behaviour of x0 as a function of
p1 and of the pressure ratio for a density normalization
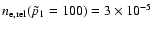 cm-3.
High values of the ratio
cm-3.
High values of the ratio
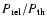 produce a substantial displacement of
x0 up to values
produce a substantial displacement of
x0 up to values
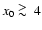 which correspond to frequencies
which correspond to frequencies
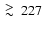 GHz.
In Fig. 21 we also show the behaviour of x0 a a
function of
GHz.
In Fig. 21 we also show the behaviour of x0 a a
function of
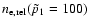 for p1=0.5. We also report in Table 9 the values of the density and the corresponding values of
for p1=0.5. We also report in Table 9 the values of the density and the corresponding values of
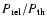 and of
and of
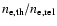 as well as the frequency position
of the zero of the total SZ effect.
It is interesting to note in this context that the precise detection of the
frequency location of x0 provides a direct measure of the ratio
as well as the frequency position
of the zero of the total SZ effect.
It is interesting to note in this context that the precise detection of the
frequency location of x0 provides a direct measure of the ratio
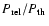 and,
in turn, of the energy density and of the properties of the spectrum of the
non-thermal population once the pressure of the thermal population is known from
X-ray observations.
In fact, all these physical information contributes to set the specific
amplitude and the spectral shape of the total SZ effect (see Figs. 17 and 20 and
Figs. 16, 18 and 20 for the different SZ effect features produced by two
different non-thermal electron populations).
This is a relevant and unique feature of the non-thermal SZ
effect in clusters since it yields a measure of the total pressure in
relativistic non-thermal particles in the cluster atmosphere, an information
which is not easily accessible from the study of other non-thermal phenomena
like radio halos and/or EUV or hard X-ray excesses. Thus, the detailed
observations of the frequency shift of x0 in clusters provides unambiguously
relevant constraints to the relativistic particle content in the ICM and to their
energy distribution. Such a measurement is also crucial to determine the true
amount of kinematic SZ effect due to the cluster peculiar velocity since it is
usually estimated from the residual SZ signal at the location of the zero of the
thermal (relativistic) SZ effect. Due to the steepness of the SZ spectral shape
in the region of the null of the overall SZ effect, the possible additional
non-thermal SZ signal must be determined precisely in order to derive reliable
limits to the kinematic SZ effect. We will present a more detailed analysis of the kinematic SZ effect in a forthcoming paper.
and,
in turn, of the energy density and of the properties of the spectrum of the
non-thermal population once the pressure of the thermal population is known from
X-ray observations.
In fact, all these physical information contributes to set the specific
amplitude and the spectral shape of the total SZ effect (see Figs. 17 and 20 and
Figs. 16, 18 and 20 for the different SZ effect features produced by two
different non-thermal electron populations).
This is a relevant and unique feature of the non-thermal SZ
effect in clusters since it yields a measure of the total pressure in
relativistic non-thermal particles in the cluster atmosphere, an information
which is not easily accessible from the study of other non-thermal phenomena
like radio halos and/or EUV or hard X-ray excesses. Thus, the detailed
observations of the frequency shift of x0 in clusters provides unambiguously
relevant constraints to the relativistic particle content in the ICM and to their
energy distribution. Such a measurement is also crucial to determine the true
amount of kinematic SZ effect due to the cluster peculiar velocity since it is
usually estimated from the residual SZ signal at the location of the zero of the
thermal (relativistic) SZ effect. Due to the steepness of the SZ spectral shape
in the region of the null of the overall SZ effect, the possible additional
non-thermal SZ signal must be determined precisely in order to derive reliable
limits to the kinematic SZ effect. We will present a more detailed analysis of the kinematic SZ effect in a forthcoming paper.


Up: The non-thermal Sunyaev-Zel'dovich effect
Copyright ESO 2003
![]() 150 MeV which do
not appreciably loose energy through Coulomb collisions in the ICM (see, e.g.,
Blasi & Colafrancesco 1999; Colafrancesco & Mele 2001) and hence do not
produce a substantial heating of the IC gas. Electrons with
150 MeV which do
not appreciably loose energy through Coulomb collisions in the ICM (see, e.g.,
Blasi & Colafrancesco 1999; Colafrancesco & Mele 2001) and hence do not
produce a substantial heating of the IC gas. Electrons with
![]() MeV
loose energy mainly through ICS and synchrotron losses. The radio halo emission
in galaxy clusters is, in fact, produced by electrons with energy
MeV
loose energy mainly through ICS and synchrotron losses. The radio halo emission
in galaxy clusters is, in fact, produced by electrons with energy
![]() (see, e.g., Colafrancesco
& Mele 2001) which yield
(see, e.g., Colafrancesco
& Mele 2001) which yield
![]() -52 GeV for a typical IC magnetic
field at the level of
-52 GeV for a typical IC magnetic
field at the level of ![]() G at the typical frequencies,
G at the typical frequencies,
![]() -10 GHz, at which radio halo spectra are observed. For such energies
the non-thermal electrons do not strongly affect the thermal IC gas. However, we
discuss in the following the impact of different non-thermal population spectra
on both the total SZ effect and on the cluster IC gas.
-10 GHz, at which radio halo spectra are observed. For such energies
the non-thermal electrons do not strongly affect the thermal IC gas. However, we
discuss in the following the impact of different non-thermal population spectra
on both the total SZ effect and on the cluster IC gas.
![]() we expect that the total SZ effect is given by
the sum of the first order SZ effects due to each single population.
At higher order approximation in
we expect that the total SZ effect is given by
the sum of the first order SZ effects due to each single population.
At higher order approximation in ![]() ,
however, one has to consider the effect
of repeated scattering (see Sect.2). It is intuitive to think that in this last
case the total SZ effect is not simply given by the sum of the separate SZ
effects at higher orders in
,
however, one has to consider the effect
of repeated scattering (see Sect.2). It is intuitive to think that in this last
case the total SZ effect is not simply given by the sum of the separate SZ
effects at higher orders in ![]() and the terms describing the
cross-scattering between CMB photons and the electrons of populations A and B
have to be taken into account. In the following, we will derive in detail the
general expression for the total SZ distortion caused by a combination of two
electronic populations.
and the terms describing the
cross-scattering between CMB photons and the electrons of populations A and B
have to be taken into account. In the following, we will derive in detail the
general expression for the total SZ distortion caused by a combination of two
electronic populations.
![]() and
and
![]() with optical depths
with optical depths
![]() and
and
![]() ,
respectively. We also
assume that the two electron distributions are both normalized to 1. The total
distribution of the electron momenta is
,
respectively. We also
assume that the two electron distributions are both normalized to 1. The total
distribution of the electron momenta is
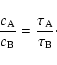
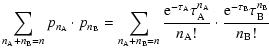
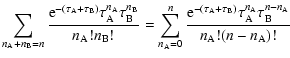
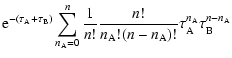
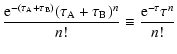
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{distorslp2.eps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg284.gif)
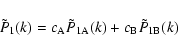
![$\displaystyle {\rm e}^{-(\tau_{\rm A}+\tau_{\rm B})\left[1-
\frac{\tau_{\rm A}}...
...)- \frac{\tau_{\rm B}}{\tau_{\rm A}+\tau_{\rm B}}\tilde{P}_{\rm 1B}(k) \right]}$](/articles/aa/full/2003/01/aah3710/img290.gif)
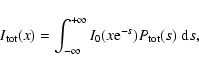
![]() and of a
spectral function
and of a
spectral function
![]() ,
in the form of Eq. (22). For two electron
populations, we can write the average temperature in Eq. (46) as:
,
in the form of Eq. (22). For two electron
populations, we can write the average temperature in Eq. (46) as:
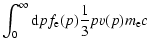
![$\displaystyle \int_0^\infty {\rm d}p
\left[c_{\rm A}f_{\rm A}(p)+c_{\rm B}f_{\rm B}(p) \right] \frac{1}{3} p v(p) m_{\rm e} c$](/articles/aa/full/2003/01/aah3710/img301.gif)
![]() keV,
keV,
![]() cm-3 and a cluster radius of
1
h50-1 Mpc. With these parameters the optical depth of the thermal
population is
cm-3 and a cluster radius of
1
h50-1 Mpc. With these parameters the optical depth of the thermal
population is
![\begin{displaymath}\tau_{\rm th}\simeq 6\times 10^{-3}
\left[\frac{n_{\rm e,th}}...
...3}}\right] \left[
\frac{\ell}{1~h_{50}^{-1}~{\rm Mpc}}\right],
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img310.gif)
![\begin{displaymath}P_{\rm th}\simeq 2.55\times10^{-2} ~{\rm keV ~cm}^{-3} \left[...
... \left[
\frac{k_{\rm B} T_{\rm e}}{8.5~ {\rm keV}}\right]\cdot
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img311.gif)
![]() while for
while for
![]() the total SZ effect
is indistinguishable from the pure thermal effect. In fact, for
the total SZ effect
is indistinguishable from the pure thermal effect. In fact, for
![]() the function P1(s) is nearly coincident with that of a single thermal
population as shown in Fig. 15, while for p1 <10 the
function P1(s) is more a-symmetric towards large and positive values of s.
The peaks of the non-thermal distributions at large s are present in the total
distribution P1(s) but their amplitude decreases with
the function P1(s) is nearly coincident with that of a single thermal
population as shown in Fig. 15, while for p1 <10 the
function P1(s) is more a-symmetric towards large and positive values of s.
The peaks of the non-thermal distributions at large s are present in the total
distribution P1(s) but their amplitude decreases with
![]() and becomes lower and lower with increasing values of p1.
and becomes lower and lower with increasing values of p1.
![\begin{figure}
\par\includegraphics[width=8cm,height=5.43cm,clip]{prob1sa-tlp1.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg316.gif)
![]() for the non-thermal population induce large
distortions with respect to the pure thermal SZ effect. However, for low values
of p1 the pressure of the non-thermal population with single power-law
distribution exceeds substantially the thermal pressure
for the non-thermal population induce large
distortions with respect to the pure thermal SZ effect. However, for low values
of p1 the pressure of the non-thermal population with single power-law
distribution exceeds substantially the thermal pressure
![]() (see Table 7); as a consequence, the low energy electrons produce an
exceedingly large pressure unbalance and also a large heating of the IC gas,
which are not acceptable.
(see Table 7); as a consequence, the low energy electrons produce an
exceedingly large pressure unbalance and also a large heating of the IC gas,
which are not acceptable.
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,height=5.96cm,clip]{distorsa...
...includegraphics[width=7cm,height=5.96cm,clip]{distorsb-tlp1.eps} }
\end{figure}](/articles/aa/full/2003/01/aah3710/Timg318.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,height=5.97cm,clip]{zeri_2po...
...graphics[width=7cm,height=5.97cm,clip]{zeri_2pop_press_tlp1b.ps} }
\end{figure}](/articles/aa/full/2003/01/aah3710/Timg320.gif)
![]() always remains of order 10-2 even for vary low values
always remains of order 10-2 even for vary low values
![]() (see Table 8), and in this case there is a
negligible dynamical and thermal influence of the non-thermal population on the
thermal one.
(see Table 8), and in this case there is a
negligible dynamical and thermal influence of the non-thermal population on the
thermal one.
![\begin{figure}
\par\includegraphics[width=8.8cm,height=5.72cm,clip]{distors-tlp2...
...\includegraphics[width=8.8cm,height=5.72cm,clip]{distors-tlp2-c.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg321.gif)
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm,clip]{dist-bc-tlp2.eps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg330.gif)