

Up: The non-thermal Sunyaev-Zel'dovich effect
In this appendix, we derive detailed expressions for
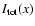 which are
approximated at first and second order in
which are
approximated at first and second order in  according to the general
expression:
according to the general
expression:
![\begin{displaymath}
I(x)=I_0(x)+\tau[J_1(x)-J_0(x)]+\frac{1}{2}\tau^2[J_2(x)-2J_1(x)+J_0(x)].
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img466.gif) |
(A.1) |
We remind the reader that the function J1(x) is given by Eq. (18):
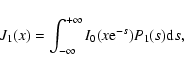 |
(A.2) |
where P1(s) is given by Eq. (5):
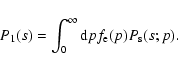 |
(A.3) |
Inserting Eq. (52) in the previous equation for P1(s), we obtain:
Inserting Eq. (A.4) in Eq. (A.2), we also obtain the expression:
Inserting Eqs. (A.5), (55) and (54) in
Eq. (A.1), we derive, at first order in  ,
the expression:
,
the expression:
As expected, the SZ effect at first order in  is given
by the sum of the separate SZ effects produced by the
two electron distributions, respectively.
is given
by the sum of the separate SZ effects produced by the
two electron distributions, respectively.
To evaluate the effect at second order in  ,
it is necessary to calculate the expression:
,
it is necessary to calculate the expression:
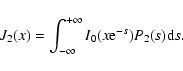 |
(A.7) |
The function P2(s) can be derived by Eq. (6) using Eq. (A.4):
Inserting this expression in Eq. (A.7), we obtain:
From Eq. (A.1) we derive the expression of the second order correction to
the total distorted spectrum
Notice that at second order in  there is an additional term describing the
probability that a CMB photon can suffer first a scattering from the electrons
of the distribution
there is an additional term describing the
probability that a CMB photon can suffer first a scattering from the electrons
of the distribution 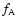 and then another scattering from the electrons of the
distribution
and then another scattering from the electrons of the
distribution 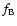 .
.
In a similar approach, we can derive the further corrections to the total
distorted spectrum evaluated at any order in  ;
these will contain a larger
and larger number of cross-scattering terms. In a completely analogous way, we
can also consider the case of three and more electron distributions.
;
these will contain a larger
and larger number of cross-scattering terms. In a completely analogous way, we
can also consider the case of three and more electron distributions.


Up: The non-thermal Sunyaev-Zel'dovich effect
Copyright ESO 2003
![]() which are
approximated at first and second order in
which are
approximated at first and second order in ![]() according to the general
expression:
according to the general
expression:
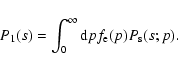
![]() ,
it is necessary to calculate the expression:
,
it is necessary to calculate the expression:
![]() ;
these will contain a larger
and larger number of cross-scattering terms. In a completely analogous way, we
can also consider the case of three and more electron distributions.
;
these will contain a larger
and larger number of cross-scattering terms. In a completely analogous way, we
can also consider the case of three and more electron distributions.