In this section we derive a generalized expression for the SZ effect which is
valid in the Thomson limit for a generic electron population in the relativistic
limit and includes also the effects of multiple scattering. First we consider an
expansion in series for the distorted spectrum I(x) in terms of the optical
depth, ![]() ,
of the electron population. Then, we consider an exact derivation
of the spectral distortion using the Fourier Transform method already outlined
in Birkinshaw (1999).
,
of the electron population. Then, we consider an exact derivation
of the spectral distortion using the Fourier Transform method already outlined
in Birkinshaw (1999).
An electron with momentum
![]() ,
with
,
with
![]() and
and
![]() increases the frequency
increases the frequency ![]() of a scattered CMB photon on
average by the factor
of a scattered CMB photon on
average by the factor
![]() ,
where
,
where ![]() and
and ![]() are the photon frequencies after and before the
scattering, respectively. Thus, in
the Compton scattering against relativistic electrons (
are the photon frequencies after and before the
scattering, respectively. Thus, in
the Compton scattering against relativistic electrons (
![]() )
a CMB photon is effectively removed from the CMB spectrum and is found at much higher
frequencies.
)
a CMB photon is effectively removed from the CMB spectrum and is found at much higher
frequencies.
We work here in the Thomson limit, (in the electron's
rest frame
![]() ), which is valid for the
interesting range of frequencies at which SZ observations are feasible.
), which is valid for the
interesting range of frequencies at which SZ observations are feasible.
The redistribution function of the CMB photons scattered once by the IC
electrons writes in the relativistic limit as,
In the following we will derive the expression for the distorted spectrum using
first an expansion in series of ![]() and then the exact formulas obtained with
the Fourier Transform (FT) method.
and then the exact formulas obtained with
the Fourier Transform (FT) method.
In the calculation of the SZ effect in galaxy clusters it is usual to use the
expression of P(s) which is derived in the single scattering approximation and
in the diffusion limit,
![]() .
In these limits, the distorted spectrum
writes, in our formalism, as:
.
In these limits, the distorted spectrum
writes, in our formalism, as:
| (10) |
The redistribution function P(s) can also be obtained in an exact form
considering all the terms of the series expansion in Eq. (14). In
fact, since the Fourier transform (hereafter FT) of a convolution product of two
functions is equal to the product of the Fourier transforms of the two
functions, the FT of P(s) writes as
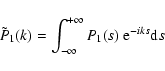 |
(20) |
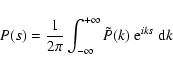 |
(21) |
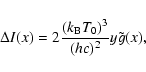 |
(22) |
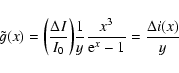 |
(23) |
For a thermal electron population in the non-relativistic limit with momentum distribution
![]() with
with
![]() ,
one writes the pressure as
,
one writes the pressure as
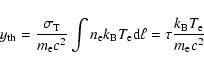 |
(26) |
In the same line, it is possible to write the expression of
![]() up to higher orders in
up to higher orders in ![]() .
For example, limiting the series
expansion in Eq. (14) at third order in
.
For example, limiting the series
expansion in Eq. (14) at third order in ![]() ,
we found:
,
we found:
![$\displaystyle \tilde{g}(x)=\frac{m_{\rm e} c^2}{ k_{\rm B} T_{\rm e} }
\left[(j...
...frac{1}{2}\tau(j_2-2j_1+j_0) +\frac{1}{6}\tau^2 (j_3-3j_2+3j_1-j_0)\right]\cdot$](/articles/aa/full/2003/01/aah3710/img137.gif) |
(28) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{gtilde.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg139.gif) |
Figure 1:
The function g(x) (solid line) is compared with the function
|
|
|
|
|
|
|
|
| x=2.3 | 7.20 | 3.68 | 2.26 | 1.57 | 0.93 |
| x=6.5 | 14.81 | 7.28 | 4.33 | 2.87 | 1.40 |
| x=15 | 64.84 | 45.99 | 32.67 | 23.87 | 13.15 |
It is worth to notice that while in the non-relativistic case it is possible to
separate the spectral dependence of the effect (which is contained in the
function g(x)) from the dependence on the cluster parameters (which are
contained in Compton parameter
![]() ,
see Eqs. (1)-(3)), this is no longer
valid in the relativistic case in which the function J1 depends itself also
on the cluster parameters. Specifically, for a thermal electron distribution,
J1 depends non-linearly from the electron temperature
,
see Eqs. (1)-(3)), this is no longer
valid in the relativistic case in which the function J1 depends itself also
on the cluster parameters. Specifically, for a thermal electron distribution,
J1 depends non-linearly from the electron temperature ![]() through the
function P1(s). This means that, even at first order in
through the
function P1(s). This means that, even at first order in ![]() ,
the spectral
shape
,
the spectral
shape
![]() of the SZ effect depends on the cluster parameters, and
mainly from the electron pressure
of the SZ effect depends on the cluster parameters, and
mainly from the electron pressure
![]() .
.
To evaluate the errors done by using the non-relativistic expression g(x)instead of the relativistic, correct function
![]() given in
Eq. (29) we calculate the fractional error
given in
Eq. (29) we calculate the fractional error
![]() for thermal populations with
for thermal populations with
![]() ,
5, 3, 2 and 1 keV and for three representative frequencies (see Table 1).
The fractional errors in Table 1 tend to decrease systematically at each
frequency with decreasing temperature. Note, however, that the error found in
the high frequency region, x=15, is much higher than the errors found at lower
frequencies and produces uncertainty levels of
,
5, 3, 2 and 1 keV and for three representative frequencies (see Table 1).
The fractional errors in Table 1 tend to decrease systematically at each
frequency with decreasing temperature. Note, however, that the error found in
the high frequency region, x=15, is much higher than the errors found at lower
frequencies and produces uncertainty levels of
![]() 50 % for
50 % for
![]() keV. This indicates that the high frequency region of the SZ effect is more
affected by the relativistic corrections and by multiple scattering effects.
In Table 2 we show the fractional error
keV. This indicates that the high frequency region of the SZ effect is more
affected by the relativistic corrections and by multiple scattering effects.
In Table 2 we show the fractional error
![]() done when considering the
exact calculation of the thermal SZ effect and those at first, second and third
order approximations in
done when considering the
exact calculation of the thermal SZ effect and those at first, second and third
order approximations in ![]() for two values of the optical depth,
for two values of the optical depth,
![]() and
and
![]() ,
as reported in the table caption. Even for the
highest cluster temperatures here considered,
,
as reported in the table caption. Even for the
highest cluster temperatures here considered,
![]() keV, the
difference between the exact and approximated calculations is
keV, the
difference between the exact and approximated calculations is
![]() 0.25%
at the minimum of the SZ effect (
0.25%
at the minimum of the SZ effect (
![]() )
and is
)
and is
![]() 2.23% in the
high-frequency tail (
2.23% in the
high-frequency tail (![]() ), the two frequency ranges where the largest
deviations are expected and could be measurable, in principle. For
high-temperature clusters, the third-order approximated calculations of the SZ
effect ensures a precision
), the two frequency ranges where the largest
deviations are expected and could be measurable, in principle. For
high-temperature clusters, the third-order approximated calculations of the SZ
effect ensures a precision
![]() at any interesting frequency.
at any interesting frequency.
Using the general, exact relativistic approach discussed in this section, we
evaluate the frequency location of the zero of the thermal SZ effect, x0, for
different cluster temperatures in the range 2-20 keV. The frequency location
of x0 depends on the IC gas temperature (or more generally on the IC gas
pressure) and in Fig. 2 we compare the temperature dependence
of x0 evaluated at first order in ![]() (which actually does not depend on
(which actually does not depend on
![]() )
with that evaluated in the exact approach for values
)
with that evaluated in the exact approach for values
![]() and
and
![]() .
.
| First order | Second order | Third order | |
|
|
|||
|
|
|||
| x=2.3 | 0.31 | 0.22 | 0.22 |
| x=6.5 | 0.12 | 0.27 | 0.27 |
| x=15 | 2.23 | 1.71 | 1.71 |
|
|
|||
|
|
|||
| x=2.3 | 0.24 | 0.23 | 0.23 |
| x=6.5 | 0.21 | 0.23 | 0.23 |
| x=15 | 0.23 | 0.18 | 0.18 |
|
|
|||
|
|
|||
| x=2.3 | 0.02 | 0.02 | 0.02 |
| x=6.5 | 0.7 | 0.02 | 0.02 |
| x=15 | 0.74 | 0.21 | 0.21 |
|
|
|||
|
|
|||
| x=2.3 | 0.01 | 0.01 | 0.01 |
| x=6.5 | 0.01 | 0.02 | 0.01 |
| x=15 | 0.31 | 0.25 | 0.25 |
| a | b | c | |
| Exact
|
3.8271 | 4.6059 | -4.8221 |
| Exact
|
3.8262 | 4.6704 | -5.4895 |
| First order | 3.8294 | 4.4304 | -1.7805 |
For ![]() ,
the expression for x0 derived by Dolgov et al. (2000)
writes as
,
the expression for x0 derived by Dolgov et al. (2000)
writes as
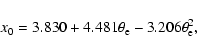 |
(30) |
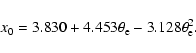 |
(31) |
Copyright ESO 2003