Compton scattering of the Cosmic Microwave Background (CMB) radiation by hot Intra Cluster (hereafter IC) electrons - the Sunyaev Zel'dovich effect (Zel'dovich & Sunyaev 1969; Sunyaev & Zel'dovich 1972, 1980) - is an important process whose spectral imprint on the CMB can be used as a powerful astrophysical and cosmological probe (see Birkinshaw 1999 for a review). Such a scattering produces a systematic shift of the CMB photons from the Rayleigh-Jeans (RJ) to the Wien side of the spectrum.
An approximate description of the scattering of an isotropic Planckian radiation field by a non-relativistic
Maxwellian electron population can be obtained by means of the solution of the Kompaneets (1957) equation (see,
e.g., Sunyaev & Zel'dovich 1980). The resulting change in the spectral intensity,
![]() ,
due to the
scattering of CMB photons by a thermal electron distribution can be written as
,
due to the
scattering of CMB photons by a thermal electron distribution can be written as
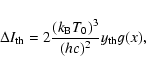 |
(1) |
![\begin{displaymath}g(x) = {x^4 {\rm e}^x \over ({\rm e}^x -1)^2} \bigg[x {{\rm e}^x +1 \over {\rm e}^x -1} -4\bigg]
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img59.gif) |
(2) |
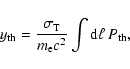 |
(4) |
The previous description of the thermal SZ effect is obtained under the Kompaneets (1957) approximation and in
the single scattering regime of the true photon redistribution function. As
such, it only provides an approximation of the SZ effect in galaxy clusters for
low temperatures (
![]() keV) and low optical depth (
keV) and low optical depth (
![]() ).
).
However, recent X-ray observations have revealed the existence of many
high-temperature clusters (David et al. 1993; Arnaud et al. 1994; Markevitch et al. 1994; Mushotzky & Scharf 1997) with
![]() up to
up to ![]() keV (see,
e.g., Tucker et al. 1998). Thus, the calculation of the thermal SZ effect from
these hot clusters requires us to take into account the appropriate relativistic
corrections (see Birkinshaw 1999 and references therein).
keV (see,
e.g., Tucker et al. 1998). Thus, the calculation of the thermal SZ effect from
these hot clusters requires us to take into account the appropriate relativistic
corrections (see Birkinshaw 1999 and references therein).
Analytical expressions for
the SZ effect in the relativistic case have been considered by various authors
(Stebbins 1997; Itoh et al. 1998; Challinor & Lasenby 1998; see also Birkinshaw
1999 and references therein). Some of these calculations (out of the Monte Carlo
simulations) are still approximate since they have been carried out in the
following limits: i) single scattering of CMB photons against the IC gas
electrons; ii) diffusion limit in which the use of the Kompaneets equation
is justified. Itoh et al. (1998) obtained higher-order relativistic corrections
to the thermal SZ effect in the form of a Fokker-Planck expansion (generalised
Kompaneets equation) and by direct integration of the Boltzmann collision term.
Such an integration has been carried out in the full relativistic regime. So,
the results of Itoh et al. (1998) can be regarded as exact in the framework of
the single scattering approximation. Analytical fitting formulae of such
derivation can be found in Nozawa et al. (2000) and Itoh et al. (2002).
Such a formalism seems to offer a detailed description of the thermal SZ effect
for
![]() keV, while Monte Carlo simulations describe more
correctly the thermal SZ effect even for
keV, while Monte Carlo simulations describe more
correctly the thermal SZ effect even for
![]() keV (see, e.g.,
Challinor & Lasenby 1998). Recently, Dolgov et al. (2001) proposed an approach
based on an analytical reduction of the collision integral which is contained in
the Boltzmann-like collision equation for the SZ effect produced by a thermal
population of electrons. They found a numerical solution for the thermal SZ
effect which is valid for generic values of
keV (see, e.g.,
Challinor & Lasenby 1998). Recently, Dolgov et al. (2001) proposed an approach
based on an analytical reduction of the collision integral which is contained in
the Boltzmann-like collision equation for the SZ effect produced by a thermal
population of electrons. They found a numerical solution for the thermal SZ
effect which is valid for generic values of ![]() and
and ![]() .
Sazonov & Sunyaev (2000) presented a derivation of the monochromatic
redistribution function in the mildly relativistic limit which considers also
quantum effects and the use of the Klein-Nishina cross-section. However, they
still consider only the single Compton scattering limit and the relativistic
corrections up to some intermediate order due to low-energy photons and
relativistic electrons. Such derivation of the monochromatic redistribution
function in the limit
.
Sazonov & Sunyaev (2000) presented a derivation of the monochromatic
redistribution function in the mildly relativistic limit which considers also
quantum effects and the use of the Klein-Nishina cross-section. However, they
still consider only the single Compton scattering limit and the relativistic
corrections up to some intermediate order due to low-energy photons and
relativistic electrons. Such derivation of the monochromatic redistribution
function in the limit
![]() reproduces the results of Fargion et
al. (1997).
More recently, Itoh et al. (2001) also presented a calculation of the thermal SZ
effect which considers the contribution from multiple scattering in the
relativistic limit. These last authors concluded that the multiple scattering
contribution to the thermal SZ effect is negligible in galaxy clusters.
reproduces the results of Fargion et
al. (1997).
More recently, Itoh et al. (2001) also presented a calculation of the thermal SZ
effect which considers the contribution from multiple scattering in the
relativistic limit. These last authors concluded that the multiple scattering
contribution to the thermal SZ effect is negligible in galaxy clusters.
Another general assumption which is made in the calculation of the SZ effect is
the use of a single population of thermal electrons which constitutes the hot
(with temperature
![]() -108 K), optically thin (with density
-108 K), optically thin (with density
![]() -10-2 cm-3, and size
-10-2 cm-3, and size ![]() a few Mpc) Intra Cluster
Medium (hereafter ICM). This assumption is based on the evidence that the IC gas
is mainly constituted by thermal electrons (and protons) which are responsible
for the X-ray emission observed in many clusters through thermal bremsstrahlung
radiation (see Sarazin 1988 for a review).
a few Mpc) Intra Cluster
Medium (hereafter ICM). This assumption is based on the evidence that the IC gas
is mainly constituted by thermal electrons (and protons) which are responsible
for the X-ray emission observed in many clusters through thermal bremsstrahlung
radiation (see Sarazin 1988 for a review).
Nonetheless, in addition to the thermal IC gas, many galaxy clusters contain a
population of relativistic electrons which produce a diffuse radio emission
(radio halos and/or relics) via synchrotron radiation in a magnetized ICM (see,
e.g., Feretti 2000 for a recent observational review). The electrons which are
responsible for the radio halo emission must have energies
![]() a few
GeV to radiate at frequencies
a few
GeV to radiate at frequencies
![]() MHz in order to reproduce the main
properties of the observed radio halos (see, e.g., Blasi & Colafrancesco 1999;
Colafrancesco & Mele 2001, and references therein). A few nearby clusters also
show the presence of an EUV/soft X-ray excess (Lieu et al. 1999; Kaastra et al.
1999 2002; Bowyer 2000) and of an hard X-ray excess (Fusco-Femiano et al.
1999-2000; Rephaeli et al. 1999; Kaastra et al. 1999; Henriksen 1999) over the
thermal bremsstrahlung radiation. These emission excesses over the thermal X-ray
emission may be produced either by Inverse Compton Scattering (hereafter ICS) of
CMB photons off an additional population of relativistic electrons or by a
combination of thermal (reproducing the EUV excess, Lieu et al. 2000) and
suprathermal (reproducing the hard X-ray excess by non-thermal bremsstrahlung,
Blasi et al. 2000; Dogiel 2000; Sarazin & Kempner 2000) populations of distinct
origins.
However, since the inefficient non-thermal bremsstrahlung mechanism would
require a large energy input and thus imply an excessive heating of the IC gas
- which is not observed - a more complex electron population is
required to fit both the radio halo and the EUV/hard X-ray spectra of galaxy
clusters (Petrosian 2001). The high-energy part (
MHz in order to reproduce the main
properties of the observed radio halos (see, e.g., Blasi & Colafrancesco 1999;
Colafrancesco & Mele 2001, and references therein). A few nearby clusters also
show the presence of an EUV/soft X-ray excess (Lieu et al. 1999; Kaastra et al.
1999 2002; Bowyer 2000) and of an hard X-ray excess (Fusco-Femiano et al.
1999-2000; Rephaeli et al. 1999; Kaastra et al. 1999; Henriksen 1999) over the
thermal bremsstrahlung radiation. These emission excesses over the thermal X-ray
emission may be produced either by Inverse Compton Scattering (hereafter ICS) of
CMB photons off an additional population of relativistic electrons or by a
combination of thermal (reproducing the EUV excess, Lieu et al. 2000) and
suprathermal (reproducing the hard X-ray excess by non-thermal bremsstrahlung,
Blasi et al. 2000; Dogiel 2000; Sarazin & Kempner 2000) populations of distinct
origins.
However, since the inefficient non-thermal bremsstrahlung mechanism would
require a large energy input and thus imply an excessive heating of the IC gas
- which is not observed - a more complex electron population is
required to fit both the radio halo and the EUV/hard X-ray spectra of galaxy
clusters (Petrosian 2001). The high-energy part (
![]() GeV) of such
spectrum contains non-thermal electrons and produce synchrotron radio emission
which can fit the observed radio-halo features: this is the best studied region
of the non-thermal spectrum in galaxy clusters.
GeV) of such
spectrum contains non-thermal electrons and produce synchrotron radio emission
which can fit the observed radio-halo features: this is the best studied region
of the non-thermal spectrum in galaxy clusters.
Indeed, in many of the clusters in which the SZ effect has been detected there is also evidence for radio halo sources (see Colafrancesco 2002). So it is of interest to assess whether the detected SZ effect is in fact mainly produced by the thermal electron population or there is a relevant contribution from other non-thermal electron populations. We will show specifically in this paper that each one of the electron populations which reside in the cluster atmosphere produces a distinct SZ effect with peculiar spectral and spatial features.
The description of the non-thermal SZ effect produced by a single electron population with a non-thermal spectrum has been attempted by various authors (McKinnon et al. 1991; Birkinshaw 1999; Ensslin & Kaiser 2000; Blasi et al. 2000). Several limits to the non-thermal SZ effect are available in the literature (see, e.g., Birkinshaw 1999 for a review) from observations of galaxy clusters which contain powerful radio halo sources (such as A2163) or radio galaxies (such as A426), but only a few detailed analysis of the results (in terms of putting limits to the non-thermal SZ effect) have been possible so far. Only a single devoted search for the SZ effect expected from a relativistic population of electrons in the lobes of bright radio galaxies has been attempted to date (McKinnon et al. 1991). No signals were seen and a detailed spectral fit of the data to separate residual synchrotron and SZ effect signals was not done, so that the limits on the SZ effect do not strongly constrain the electron populations in the radio lobes. Also the problem of detecting the non-thermal SZ effect in radio-halo clusters is likely to be severe because of the associated synchrotron radio emission. In fact, at low radio frequencies, such a synchrotron emission could easily dominate over the small negative signal produced by the SZ effect. At higher frequencies there is in principle more chance to detect the non-thermal SZ effect, but even here there are likely to be difficulties in separating the SZ effect from the flat-spectrum component of the synchrotron emission (Birkinshaw 1999).
From the theoretical point of view, preliminary calculations (Birkinshaw 1999;
Ensslin & Kaiser 2000; Blasi et al. 2000) of the non-thermal SZ effect have
been carried out in the diffusion approximation (
![]() ), in the limit of
single scattering and for a single non-thermal population of electrons.
Specifically, Ensslin & Kaiser (2000) and Blasi et al. (2000) considered the SZ
effect produced under the previous approximations by a supra-thermal tail of the Maxwellian electron distribution
claimed to exist in the Coma cluster and
concluded that the SZ effect, even though of small amplitude, could be measurable
in the sub-mm region by the next coming PLANCK experiment. However, Petrosian
(2001) showed that the suprathermal electron distribution faces with several
crucial problems, the main being the large heating that such electrons would
induce through Coulomb collisions in the ICM. The large energy input of the
suprathermal distribution in the ICM of Coma would heat the IC gas up to
unreasonably high temperatures,
), in the limit of
single scattering and for a single non-thermal population of electrons.
Specifically, Ensslin & Kaiser (2000) and Blasi et al. (2000) considered the SZ
effect produced under the previous approximations by a supra-thermal tail of the Maxwellian electron distribution
claimed to exist in the Coma cluster and
concluded that the SZ effect, even though of small amplitude, could be measurable
in the sub-mm region by the next coming PLANCK experiment. However, Petrosian
(2001) showed that the suprathermal electron distribution faces with several
crucial problems, the main being the large heating that such electrons would
induce through Coulomb collisions in the ICM. The large energy input of the
suprathermal distribution in the ICM of Coma would heat the IC gas up to
unreasonably high temperatures,
![]() K, which are not observed.
In addition, Colafrancesco (2002) noticed that dust obscuration does not allow any
detection of the SZ signal from Coma at frequencies
K, which are not observed.
In addition, Colafrancesco (2002) noticed that dust obscuration does not allow any
detection of the SZ signal from Coma at frequencies
![]() GHz.
GHz.
Matters are significantly more complicated if the full relativistic formalism is used. However, this is necessary, since many galaxy clusters show extended radio halos and the electrons which produce the diffuse synchrotron radio emission are certainly highly relativistic so that the use of the Kompaneets approximation is invalid. Moreover, the presence of thermal and non-thermal electrons in the same location of the ICM renders the single scattering approximation and the single population approach unreasonable, so that the treatment of multiple scattering among different electronic populations coexisting in the same cluster atmosphere is necessary to describe correctly the overall SZ effect.
Here we derive the spectral and spatial features of the SZ effect using an exact
derivation of the spectral distortion induced by a combination of a thermal and
a non-thermal population of electrons which are present at the same time in the
ICM. Lately, we also consider the case of the combination of several non-thermal
and thermal populations. The plan of the paper is the following: in Sect. 2 we
will provide a general derivation of the SZ effect in an exact formalism within
the framework of our approach, i.e., considering the fully relativistic approach
outlined in Birkinshaw (1999) and the effect induced by multiple scattering. We
work here in the Thomson limit
![]() .
Within such framework, we
derive the exact SZ effect for a single electron population both in the thermal
and non-thermal cases. In Sect. 3 we derive the SZ effect produced by a single
population of non-thermal electrons providing both exact and approximate (up to any
order in
.
Within such framework, we
derive the exact SZ effect for a single electron population both in the thermal
and non-thermal cases. In Sect. 3 we derive the SZ effect produced by a single
population of non-thermal electrons providing both exact and approximate (up to any
order in ![]() )
expressions for the non-thermal SZ effect. In Sect. 4 we derive
the total SZ effect produced by a combination of two populations: a distribution
of thermal electrons - like that responsible for the X-ray emission of galaxy
clusters - and a non-thermal electron distribution - like the one responsible
for the radio halo emission which is present in many galaxy clusters. Our
general approach allows to derive the expression for the SZ effect produced by
the combination of any electronic population. So, in Sect. 5 we consider also
the SZ effect generated by the combination of two different thermal populations.
In Sect. 6 we discuss the spatial features associated to the presence of a
non-thermal SZ effect superposed to the thermal SZ effect. In Sect. 7 we derive
limits on the presence and amplitude of the non-thermal SZ effect discussing
specifically the cases of a few clusters in which there is evidence for the
presence of non-thermal, high-energy electrons. We show how the possible
detection of a non-thermal SZ effect can set relevant constraints on the
relative electron population. We summarize our results and discuss our
conclusions in the final Sect. 8. We use H0 = 50 km s-1 Mpc-1 and
)
expressions for the non-thermal SZ effect. In Sect. 4 we derive
the total SZ effect produced by a combination of two populations: a distribution
of thermal electrons - like that responsible for the X-ray emission of galaxy
clusters - and a non-thermal electron distribution - like the one responsible
for the radio halo emission which is present in many galaxy clusters. Our
general approach allows to derive the expression for the SZ effect produced by
the combination of any electronic population. So, in Sect. 5 we consider also
the SZ effect generated by the combination of two different thermal populations.
In Sect. 6 we discuss the spatial features associated to the presence of a
non-thermal SZ effect superposed to the thermal SZ effect. In Sect. 7 we derive
limits on the presence and amplitude of the non-thermal SZ effect discussing
specifically the cases of a few clusters in which there is evidence for the
presence of non-thermal, high-energy electrons. We show how the possible
detection of a non-thermal SZ effect can set relevant constraints on the
relative electron population. We summarize our results and discuss our
conclusions in the final Sect. 8. We use H0 = 50 km s-1 Mpc-1 and
![]() throughout the paper unless otherwise specified.
throughout the paper unless otherwise specified.
Copyright ESO 2003