Using the same general analytical approach derived in Sect. 2 above we derive
here the exact spectral features of the SZ effect produced by a single
non-thermal population of electrons. Such an exact derivation has been not done
so far. For such a population we consider here two different phenomenological
spectra: i) a single power-law energy spectrum,
![]() ,
like that which is able to fit the radio-halo spectra of many
clusters, and ii) a double power-law spectrum which is able to fit both
the radio halo spectrum and the EUV and hard X-ray excess spectra observed in
some nearby clusters (see Petrosian 2001). Our formalism is, nonetheless, so
general that it can be applied to any electron distribution so far considered to
fit both the observed radio-halo spectra and those of the EUV/Hard X-ray
excesses (see, e.g., Sarazin 1999; Blasi & Colafrancesco 1999; Colafrancesco &
Mele 2001; Petrosian 2001).
,
like that which is able to fit the radio-halo spectra of many
clusters, and ii) a double power-law spectrum which is able to fit both
the radio halo spectrum and the EUV and hard X-ray excess spectra observed in
some nearby clusters (see Petrosian 2001). Our formalism is, nonetheless, so
general that it can be applied to any electron distribution so far considered to
fit both the observed radio-halo spectra and those of the EUV/Hard X-ray
excesses (see, e.g., Sarazin 1999; Blasi & Colafrancesco 1999; Colafrancesco &
Mele 2001; Petrosian 2001).
The single power-law electron population is described by the momentum spectrum
The distribution in Eq. (32) can be however affected by a crucial
problem: if the electron spectrum is extended at energies below 20 MeV (i.e., at
![]() )
with the same spectral slope
)
with the same spectral slope
![]() of the high
energy tail, the heating rate of the IC gas produced by Coulomb collisions of
the relativistic electrons becomes larger than the bremsstrahlung cooling rate
of the IC gas (see, e.g., Petrosian 2001). This would produce unreasonably and
unacceptably large heating of the IC gas.
of the high
energy tail, the heating rate of the IC gas produced by Coulomb collisions of
the relativistic electrons becomes larger than the bremsstrahlung cooling rate
of the IC gas (see, e.g., Petrosian 2001). This would produce unreasonably and
unacceptably large heating of the IC gas.
For this reason, we consider also a double power-law electron spectrum which has
a flatter slope below a critical value
![]() :
:
A crucial quantity in the calculation of the non-thermal SZ effect is given by
the number density of relativistic electrons,
![]() .
The quantity
.
The quantity
![]() in galaxy clusters can be estimated from the radio halo spectrum
intensity, but this estimate depends on the assumed value of the IC magnetic
field and on the model for the evolution of the radio-halo spectrum (see, e.g.
Sarazin 1999 for time-dependent models and Blasi & Colafrancesco 1999;
Colafrancesco & Mele 2001 for stationary models). For the sake of illustration,
the radio halo flux
in galaxy clusters can be estimated from the radio halo spectrum
intensity, but this estimate depends on the assumed value of the IC magnetic
field and on the model for the evolution of the radio-halo spectrum (see, e.g.
Sarazin 1999 for time-dependent models and Blasi & Colafrancesco 1999;
Colafrancesco & Mele 2001 for stationary models). For the sake of illustration,
the radio halo flux ![]() for a power-law spectrum is, in fact, given by
for a power-law spectrum is, in fact, given by
![]() ,
where
,
where
![]() is
the radio halo spectral slope. Because of the large intrinsic uncertainties
existing in the density of the relativistic electrons which produce the cluster
non-thermal phenomena, a value
is
the radio halo spectral slope. Because of the large intrinsic uncertainties
existing in the density of the relativistic electrons which produce the cluster
non-thermal phenomena, a value
![]() cm-3 for p1=100 has
been assumed here.
cm-3 for p1=100 has
been assumed here.
Our results on the amplitude of the non-thermal SZ effect can be easily rescaled
to different values of
![]() :
in fact, decreasing (increasing)
:
in fact, decreasing (increasing)
![]() will produce smaller (larger) amplitudes of the SZ effect, as can be seen from
Eqs. (22), (24), (28), (29).
will produce smaller (larger) amplitudes of the SZ effect, as can be seen from
Eqs. (22), (24), (28), (29).
The density
![]() increases for decreasing values of p1. In fact, multiplying the electron distribution in Eq. (32) by
the quantity
increases for decreasing values of p1. In fact, multiplying the electron distribution in Eq. (32) by
the quantity
![]() one obtains
one obtains
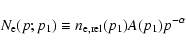 |
(36) |
The value of p1 sets the value of the electron density as well as the value
of the other relevant quantities which depend on it, namely the optical depth
![]() and the pressure
and the pressure
![]() of the non-thermal population.
In particular, the pressure
of the non-thermal population.
In particular, the pressure
![]() for the case of an electron
distribution in Eq. (32), is given by
for the case of an electron
distribution in Eq. (32), is given by
![\begin{figure}
\par\includegraphics[width=8cm,clip]{problpa.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg200.gif) |
Figure 3:
The distribution P1(s) for
a non-thermal population as in Eq. (32) with
|
![\begin{figure}
\par\mbox{\includegraphics[width=6.8cm,height=5.77cm,clip]{p3lp.e...
...e*{2mm}
\includegraphics[width=6.8cm,height=5.77cm,clip]{3Ps.ps} }
\end{figure}](/articles/aa/full/2003/01/aah3710/Timg202.gif) |
Figure 4:
The distributions P1(s) (solid line), P2(s) (dashed) and
P3(s) (dotted) evaluated for non-thermal electron populations with a single
power-law spectrum given in Eq. (32) with |
| p1 |
|
|
| 0.5 | 0.59 |
|
| 1 | 0.47 |
|
| 10 | 0.16 |
|
| 100 |
|
|
| 1000 |
|
|
To emphasize the changes in the photon redistribution function produced by a non-thermal electron distribution, we show in Fig. 4 the functions P1(s), P2(s) and P3(s) for a single and double power-law electron distributions. It is evident that these functions are wider and more a-symmetrically skewed towards large and positive values of s with respect to the same distributions evaluated in the case of a single thermal electron population. Once the exact redistribution function P(s) is known, it is possible to evaluate the exact distorted spectrum I(x) through Eq. (8).
It is also possible to evaluate the spectral distortion using Eq. (16) which
gives the series expansion up to the nth order in ![]() and to compare the
exact and approximated shapes for I(x). We show in Fig. 5 the
first three terms
b1,b2, b3 of the series expansion in Eq. (16) as a
function of the a-dimensional frequency x.
The approximated expression for I(x) up to third order in
and to compare the
exact and approximated shapes for I(x). We show in Fig. 5 the
first three terms
b1,b2, b3 of the series expansion in Eq. (16) as a
function of the a-dimensional frequency x.
The approximated expression for I(x) up to third order in ![]() is an
excellent fit of its exact behaviour at frequencies around the minimum of the
effect (
is an
excellent fit of its exact behaviour at frequencies around the minimum of the
effect (
![]() )
and it shows a difference
)
and it shows a difference ![]() 3% at
3% at
![]() and a difference
and a difference ![]() 0.1% at high frequencies,
0.1% at high frequencies,
![]() (see
Table 5). The precision of the approximation depends also on the
value of
(see
Table 5). The precision of the approximation depends also on the
value of ![]() and we verified that the precision of the second and third order
approximations does not increase for values
and we verified that the precision of the second and third order
approximations does not increase for values
![]() at any
frequency between
at any
frequency between
![]() and
and
![]() .
.
| First order | Second order | Third order | |
| x=2.3 | 0.82 | 0.44 | 0.44 |
| x=6.5 | 1.42 | 2.90 | 2.90 |
| x=15 | 0.83 | 0.12 | 0.12 |
|
|
|||
| x=2.3 | 0.49 | 0.45 | 0.45 |
| x=6.5 | 2.73 | 2.88 | 2.88 |
| x=15 | 0.19 | 0.12 | 0.12 |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{contrlp.eps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg217.gif) |
Figure 5: The functions b1(x) (solid), b2(x) (dashed) and b3(x) (dotted) evaluated for a non-thermal electron population with a single power-law spectrum as in Eq. (32). |
Also for a non-thermal electron population it is possible to write the spectral
distortion in the general form of Eq. (22) as:
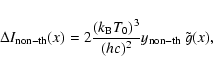 |
(43) |
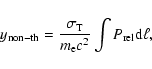 |
(44) |
At first order in ![]() we can write the spectral function
we can write the spectral function
![]() of the non-thermal SZ effect as
of the non-thermal SZ effect as
![\begin{displaymath}\langle k_{\rm B} T_{\rm e} \rangle= \frac{ m_{\rm e} c^2 (\a...
...{\alpha-2}{2},
\frac{3-\alpha}{2}\right)\right]_{p_2}^{p_1} ,
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img224.gif) |
(47) |
![$\displaystyle \langle k_{\rm B} T_{\rm e} \rangle
=\frac{K(p_1) m_{\rm e} c^2}{...
...2} \right) \right]^{p_{\rm cr}}_{p_2}
p_{\rm cr}^{-\alpha_1+\alpha_2} \right\}.$](/articles/aa/full/2003/01/aah3710/img225.gif) |
(48) |
We can also write the nth order approximations of the distorted
spectrum using Eq. (16). For example, at third order in ![]() ,
the following
explicit expression founds:
,
the following
explicit expression founds:
![$\displaystyle \tilde{g}(x)=\frac{m_{\rm e} c^2}{\langle k_{\rm B} T_{\rm e} \ra...
...rac{1}{2}\tau(j_2-2j_1+j_0) +\frac{1}{6}\tau^2
(j_3-3j_2+3j_1-j_0)\right] \cdot$](/articles/aa/full/2003/01/aah3710/img232.gif) |
(50) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{gtildenonterm.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg235.gif) |
Figure 6:
The spectral function g(x) for a thermal population
in the Kompaneets limit (solid line) is compared with the function
|
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,height=5.24cm,clip]{gtildelp...
...mm}
\includegraphics[width=7cm,height=5.24cm,clip]{gtildelpb.eps} }
\end{figure}](/articles/aa/full/2003/01/aah3710/Timg239.gif) |
Figure 8:
In the left panel we show the function
|
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,height=5.77cm,clip]{zerip1-l...
...\includegraphics[width=7cm,height=5.77cm,clip]{zeripress-lp1.ps} }
\end{figure}](/articles/aa/full/2003/01/aah3710/Timg240.gif) |
Figure 9:
The behaviour of the zero of the SZ effect for a non-thermal population
given in Eq. (32) as a function of p1 (left panel)
and of the pressure
|
For an electron population with a double power-law spectrum as in
Eq. (34) the values of the density and pressure are also reported in
Table 6 as a function of p1 (note that the case
p1=1000 is the same of the single power-law spectrum). The values of
![]() and
and
![]() for low values of p1 are now smaller than those of
the single power-law case (see Table4), thus avoiding the problem of an
excessive heating of the cluster IC gas for low values of p1.
for low values of p1 are now smaller than those of
the single power-law case (see Table4), thus avoiding the problem of an
excessive heating of the cluster IC gas for low values of p1.
| p1 |
|
|
| 0.5 |
|
|
| 1 |
|
|
| 10 |
|
|
| 100 |
|
|
In Fig. 11 we show the function P1(s) evaluated for an electron
population with double power-law spectrum (see Eq. (34)) and its dependence on the
lower momentum cutoff p1. The behaviour of P1(s) in this case is quite
different with respect to the single power-law case (see
Fig. 3) and depends mainly on the flatness of the electron
spectrum below the momentum cutoff
![]() .
We notice that i) even for
low values of
.
We notice that i) even for
low values of
![]() small frequency changes are unlikely, as shown by
the strongly a-symmetric shape of P1(s); ii) there are small
differences in the function P1(s) for different values of
small frequency changes are unlikely, as shown by
the strongly a-symmetric shape of P1(s); ii) there are small
differences in the function P1(s) for different values of
![]() because the electron density in this range is lower than in the single power-law
case and its variation is mild.
because the electron density in this range is lower than in the single power-law
case and its variation is mild.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{distorslp.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg250.gif) |
Figure 10:
The spectral distortion
|
![\begin{figure}
\par\includegraphics[width=7.3cm,height=5.3cm,clip]{prob1slp2.eps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg251.gif) |
Figure 11: The function P1(s) (see Eq. (5)) is shown for non-thermal populations given in Eq. (34) with p1= 0.5 (solid), 1 (dashes), 10 (dotted), 100 (dot-dashes). |
We finally show in
Fig. 14 the spectral distortion
![]() for different
values of p1. Note, finally, that the amplitude of
for different
values of p1. Note, finally, that the amplitude of
![]() produced by
an electron population with a double power-law spectrum as in Eq. (34)
is much lower than that produced by a population with a single power-law
spectrum as in Eq. (32).
produced by
an electron population with a double power-law spectrum as in Eq. (34)
is much lower than that produced by a population with a single power-law
spectrum as in Eq. (32).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{gtildelp2.eps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg256.gif) |
Figure 12:
The function
|
The case of a system dominated by non-thermal electrons is not applicable straightforwardly to galaxy clusters but rather to radio galaxies whose jets inject in the ICM large quantities of relativistic non-thermal electrons. We want to stress that our general approach is able to describe the Compton scattering distortions even in the cases of the radio lobes and of the jets of radio galaxies or AGNs with large optical depths and ultra-relativistic electron energies. We will address more specifically this issue in a forthcoming paper.
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,height=6.04cm,clip]{zerip1-l...
...includegraphics[width=7cm,height=6.04cm,clip]{zeripress2-lp2.ps} }
\end{figure}](/articles/aa/full/2003/01/aah3710/Timg257.gif) |
Figure 13:
The behaviour of the zero of the SZ effect for a
non-thermal population with spectrum
given by Eq. (34) as a function of p1 (left panel)
and of the pressure
|
Copyright ESO 2003