

Up: The non-thermal Sunyaev-Zel'dovich effect
In this section we want to study the effect of the superposition of two distinct
electron populations on the spatial distribution of the total SZ effect in
galaxy clusters. In fact, the thermal and the non-thermal populations have, in
general, a different spatial distribution as indicated by the spatial extension
of the X-ray emission and of the radio halo emission in many clusters (see
Giovannini et al. 2001).
Also, there are indications that the EUV emission in some nearby clusters is
more extended than the thermal X-ray emission suggesting that there is a warm
gas and/or a population of relativistic electrons which are spatially more
extended than the X-ray emitting IC gas (Lieu et al. 1999).
Let us first consider a galaxy cluster in which two different electron
populations are present: a thermal population, described by a relativistic
Maxwellian velocity distribution, and a non-thermal population, with an energy
spectrum described by a double power-law (see Eq. (34)). We consider these two
populations as independent and spatially superposed, consistently with our
analysis of Sect. 4. These assumptions are indeed reasonable since in the
cluster A2163, for instance, the radio halo emitting electrons occupy
approximately the same volume of the X-ray emitting, thermal electrons (see
Feretti et al. 2001) and, moreover, the relativistic electrons with
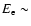 a
few GeV (which produce the radio-halo synchrotron emission) do not sensitively
affect the IC thermal electrons.
a
few GeV (which produce the radio-halo synchrotron emission) do not sensitively
affect the IC thermal electrons.
![\begin{figure}
\par\includegraphics[width=8cm,height=5.27cm,clip]{zeridens-tlp2.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg344.gif) |
Figure 21:
The behaviour of the zero of the total SZ effect
produced by a combination of a thermal and non-thermal population given in Eq. (34)
with p1=0.5 is shown as a function of
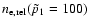 . .
|
![\begin{figure}
\par\includegraphics[width=8cm,height=5.51cm,clip]{p1s_2term_abc.eps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg345.gif) |
Figure 22:
The function P1(s) computed for a combination of two
thermal populations with
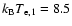 and
and
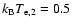 keV (solid line) and with keV (solid line) and with
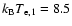 and
and
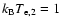 keV (dashed line) is compared with
that of the single thermal population with keV (dashed line) is compared with
that of the single thermal population with
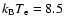 keV (dotted line). keV (dotted line).
|
![\begin{figure}
\par\includegraphics[width=8cm,height=5.7cm,clip]{dist-ae-tt1.eps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg346.gif) |
Figure 23:
The spectral distortion in units of
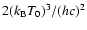 produced by a single thermal population
with
produced by a single thermal population
with
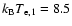 keV and keV and
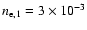 cm-3 (solid line) is
compared with that produced by a
combination of two thermal populations with cm-3 (solid line) is
compared with that produced by a
combination of two thermal populations with
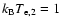 keV and keV and
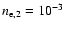 (dashed line),
(dashed line),
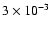 (dotted),
(dotted),
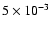 (dot-dashed),
(dot-dashed),
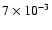 (long dashes) and 10-2 (dot-dot-dashes) cm-3.
(long dashes) and 10-2 (dot-dot-dashes) cm-3.
|
As for the spatial distribution of the thermal electrons we use here a
isothermal 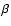 -model (see, e.g., Cavaliere & Fusco-Femiano 1976),
according to which the temperature
-model (see, e.g., Cavaliere & Fusco-Femiano 1976),
according to which the temperature 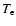 of the ICM is constant and the electron
density is described by a spherical distribution
of the ICM is constant and the electron
density is described by a spherical distribution
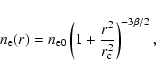 |
(69) |
where
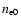 is the central IC gas density,
is the central IC gas density, 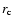 is the core radius of the
cluster and
is the core radius of the
cluster and
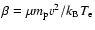 is observed in the range 0.6-1 (see Sarazin 1988 for a review). Under this assumption the angular dependence of
the optical depth of the thermal population is given by
is observed in the range 0.6-1 (see Sarazin 1988 for a review). Under this assumption the angular dependence of
the optical depth of the thermal population is given by
where 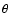 is the angle between the centre of cluster and the direction of
observation. All the angular dependence is contained in the function
is the angle between the centre of cluster and the direction of
observation. All the angular dependence is contained in the function
![\begin{displaymath}Y(\theta)=\sqrt{\pi} \frac{\Gamma\left( \frac{3}{2}\beta-\fra...
...\rm c}} \right)^2 \right]^{
\frac{1}{2} - \frac{3}{2} \beta} ,
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img356.gif) |
(71) |
where
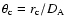 ,
in terms of the angular diameter distance
,
in terms of the angular diameter distance 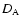 (see
Weinberg 1972).
(see
Weinberg 1972).
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,height=6cm,clip]{zeri_2term_...
...graphics[width=7cm,height=6cm,clip]{zeri_2term_press_dens_ab.ps} }
\end{figure}](/articles/aa/full/2003/01/aah3710/Timg359.gif) |
Figure 24:
The behaviour of the zero of the total SZ effect for a combination of two thermal
populations with
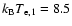 keV and keV and
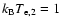 keV (solid line) and keV (solid line) and
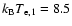 keV and keV and
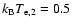 keV (dashed line) is shown as a function of the density keV (dashed line) is shown as a function of the density
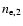 (left panel)
and of the pressure ratio P2/P1 (right panel).
A value
(left panel)
and of the pressure ratio P2/P1 (right panel).
A value
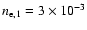 cm-3 is adopted here. cm-3 is adopted here. |
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,height=6cm,clip]{zeri_2term_...
...degraphics[width=7cm,height=6cm,clip]{zeri_2term_press_temp_.ps} }
\end{figure}](/articles/aa/full/2003/01/aah3710/Timg360.gif) |
Figure 25:
The behaviour of the zero of the total SZ effect for a combination of two thermal
populations with
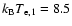 keV and keV and
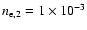 cm-3 is shown as a function of the temperature cm-3 is shown as a function of the temperature
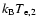 (left panel) and of the pressure
ratio P2/P1 (right panel). A value (left panel) and of the pressure
ratio P2/P1 (right panel). A value
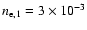 cm-3 is adopted here. cm-3 is adopted here. |
In the following we will describe in detail, for the sake of clarity, the
spatial distribution of the approximated (to first and second order in  )
expression of the total SZ effect and we will give also the general expression for the
exact calculations.
)
expression of the total SZ effect and we will give also the general expression for the
exact calculations.
The angular dependence of the SZ-induced spectral
distortion evaluated at first order in  writes as
writes as
![\begin{displaymath}
\Delta i(x,\theta)=\tau(\theta) [j_1(x)-j_0(x)] ,
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img361.gif) |
(72) |
where 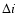 is in units of
is in units of
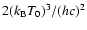 and
and
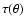 is
given by Eq. (70). Since the spectral distortion can be written
in the general form
is
given by Eq. (70). Since the spectral distortion can be written
in the general form
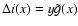 ,
the Comptonization parameter
writes as
,
the Comptonization parameter
writes as
where the quantity
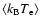 is defined in Eq. (46)
and depends only on the parameters of the electron distribution (here the
central pressure is
is defined in Eq. (46)
and depends only on the parameters of the electron distribution (here the
central pressure is
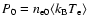 ). The spectral shape
of the SZ effect at an angular distance
). The spectral shape
of the SZ effect at an angular distance 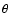 from the
cluster center can be
written, at first order in
from the
cluster center can be
written, at first order in  ,
as
,
as
and it does not contain the angular dependence of the effect.
However, at second order in  the spectral distortion writes as
the spectral distortion writes as
![\begin{displaymath}\Delta i(x,\theta)=\frac{1}{2} \tau^2(\theta) [j_2(x)-2j_1(x)+j_0(x)],
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img371.gif) |
(75) |
and, as a consequence, the second order approximation of the function
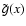 is
is
which depends explicitly on 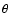 .
It is important to notice that the angular dependence of the spectral
distortion is present both in the Comptonization parameter y and in the
spectral shape
.
It is important to notice that the angular dependence of the spectral
distortion is present both in the Comptonization parameter y and in the
spectral shape
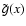 .
The dependence of the SZ effect from
.
The dependence of the SZ effect from 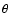 is
present at all orders n>1 of the approximations and hence in the full, exact
expression of the SZ effect. Thus, also for the study of the spatial
distribution of the total SZ effect, considering the first order approximation
is neither appropriate nor consistent.
is
present at all orders n>1 of the approximations and hence in the full, exact
expression of the SZ effect. Thus, also for the study of the spatial
distribution of the total SZ effect, considering the first order approximation
is neither appropriate nor consistent.
For a combination of two electron populations, the total spectral distortion is
given, at first order approximation in  ,
by the sum of the single spectral
distortions of each population
,
by the sum of the single spectral
distortions of each population
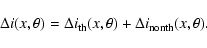 |
(77) |
This expression can be written more explicitly as
where
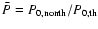 is the pressure ratio at the cluster
center. We assume here that the spatial distribution of the thermal and of the non-thermal electron populations are given by a
is the pressure ratio at the cluster
center. We assume here that the spatial distribution of the thermal and of the non-thermal electron populations are given by a 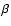 -model with core radii
-model with core radii
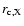 and
and
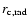 and parameters
and parameters
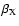 and
and
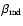 ,
respectively.
Such an expression is also valid in the case of the combination of two
thermal populations. At higher approximation orders in
,
respectively.
Such an expression is also valid in the case of the combination of two
thermal populations. At higher approximation orders in  ,
the total
spectral distortion contains cross-correlation terms of the parameters of each
population and thus it is not possible to write it as a linear combination of the
spectral distortions of the separate electron populations. An exact derivation
(or at least the 3rd order approximation in
,
the total
spectral distortion contains cross-correlation terms of the parameters of each
population and thus it is not possible to write it as a linear combination of the
spectral distortions of the separate electron populations. An exact derivation
(or at least the 3rd order approximation in  )
is required to describe
correctly the spatial dependence of the total SZ effect in galaxy clusters. The
general calculation of the spatial distribution of the total SZ effect can be
made using the exact expressions derived in Eqs. (21-23, 62, 63) in which the
spatial dependence of the thermal and non-thermal electron populations are
considered.
)
is required to describe
correctly the spatial dependence of the total SZ effect in galaxy clusters. The
general calculation of the spatial distribution of the total SZ effect can be
made using the exact expressions derived in Eqs. (21-23, 62, 63) in which the
spatial dependence of the thermal and non-thermal electron populations are
considered.
In Fig. 26 we show the spatial behaviour of the total SZ
effect in the case of a Coma-like cluster.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{spaziale_aa.ps}\par\includegraphics[width=8.8cm,clip]{spaziale_bb.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg388.gif) |
Figure 26:
The spatial dependence of the total SZ effect produced by the
combination of the
thermal and relativistic electrons in a Coma-like cluster. We show the thermal SZ effect (dots)
and the total SZ effect with
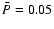 (solid), 0.49 (short dashes) and 1.48 (long dashes).
Calculations are done for an a-dimensional frequency of x=2.3 where
the total SZ effect has its minimum value (upper panel) and for x=6.5 where
the total SZ effect has its maximum value (lower panel).
(solid), 0.49 (short dashes) and 1.48 (long dashes).
Calculations are done for an a-dimensional frequency of x=2.3 where
the total SZ effect has its minimum value (upper panel) and for x=6.5 where
the total SZ effect has its maximum value (lower panel).
|
We use specifically the following parameters:
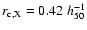 Mpc,
Mpc,
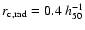 Mpc,
Mpc,
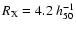 Mpc,
Mpc,
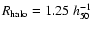 Mpc,
Mpc,
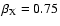 ,
,
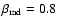 ,
,
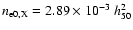 cm-3,
cm-3,
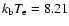 keV.
The non-thermal electron population fitting the radio halo spectrum is taken with spectral parameters
p1 = 1000 and
keV.
The non-thermal electron population fitting the radio halo spectrum is taken with spectral parameters
p1 = 1000 and
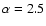 .
The total SZ effect shows a peculiar spatial behaviour which is particularly
evident at the frequencies
.
The total SZ effect shows a peculiar spatial behaviour which is particularly
evident at the frequencies
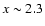 where it attains its minimum value and
at frequencies
where it attains its minimum value and
at frequencies
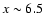 close to its maximum. At
close to its maximum. At
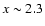 the spatial
profile of the total SZ effect is predicted to be higher than that due
only to the thermal population because the non-thermal SZ effect sums up in the
region of the radio halo which extends up to
the spatial
profile of the total SZ effect is predicted to be higher than that due
only to the thermal population because the non-thermal SZ effect sums up in the
region of the radio halo which extends up to
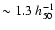 Mpc (see
Fig. 26). At larger distances from the cluster center, the SZ
effect is dominated by the thermal component and resemble its spatial behaviour.
An opposite behaviour is expected at frequencies higher than that of the zero of
the total SZ effect. For instance at
Mpc (see
Fig. 26). At larger distances from the cluster center, the SZ
effect is dominated by the thermal component and resemble its spatial behaviour.
An opposite behaviour is expected at frequencies higher than that of the zero of
the total SZ effect. For instance at
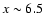 the spatial profile of the total SZ effect is lower than that of the single
thermal effect because the spectrum of the total SZ effect is lower than that of
the thermal case. So, a depression in the spatial profile of the total SZ effect
is expected at radii smaller than the radio halo extension
the spatial profile of the total SZ effect is lower than that of the single
thermal effect because the spectrum of the total SZ effect is lower than that of
the thermal case. So, a depression in the spatial profile of the total SZ effect
is expected at radii smaller than the radio halo extension
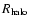 .
At distances larger than
the radio halo extension, the total SZ effect is again dominated by the thermal
component.
The amplitude of the non-thermal SZ contribution depends from the pressure ratio
.
At distances larger than
the radio halo extension, the total SZ effect is again dominated by the thermal
component.
The amplitude of the non-thermal SZ contribution depends from the pressure ratio
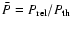 as shown in Fig. 26. Such spatial
features of the total SZ effect should be detectable with sensitive instruments
with good spatial resolution and narrow spectral frequency band. Such
instrumental capabilities can also be able to detect the transition between the
ambient thermal SZ effect and the non-thermal SZ effect expected in radio relics
and in the radio lobes of active galaxies found in the cluster environment.
as shown in Fig. 26. Such spatial
features of the total SZ effect should be detectable with sensitive instruments
with good spatial resolution and narrow spectral frequency band. Such
instrumental capabilities can also be able to detect the transition between the
ambient thermal SZ effect and the non-thermal SZ effect expected in radio relics
and in the radio lobes of active galaxies found in the cluster environment.


Up: The non-thermal Sunyaev-Zel'dovich effect
Copyright ESO 2003
![]() a
few GeV (which produce the radio-halo synchrotron emission) do not sensitively
affect the IC thermal electrons.
a
few GeV (which produce the radio-halo synchrotron emission) do not sensitively
affect the IC thermal electrons.
![\begin{figure}
\par\includegraphics[width=8cm,height=5.27cm,clip]{zeridens-tlp2.ps} \end{figure}](/articles/aa/full/2003/01/aah3710/Timg344.gif)
![]() -model (see, e.g., Cavaliere & Fusco-Femiano 1976),
according to which the temperature
-model (see, e.g., Cavaliere & Fusco-Femiano 1976),
according to which the temperature ![]() of the ICM is constant and the electron
density is described by a spherical distribution
of the ICM is constant and the electron
density is described by a spherical distribution
![\begin{displaymath}Y(\theta)=\sqrt{\pi} \frac{\Gamma\left( \frac{3}{2}\beta-\fra...
...\rm c}} \right)^2 \right]^{
\frac{1}{2} - \frac{3}{2} \beta} ,
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img356.gif)
![]() )
expression of the total SZ effect and we will give also the general expression for the
exact calculations.
)
expression of the total SZ effect and we will give also the general expression for the
exact calculations.
![]() writes as
writes as
![$\displaystyle \frac{m_{\rm e} c^2}{\langle k_{\rm B} T_{\rm e} \rangle} [j_1(x)-j_0(x)],$](/articles/aa/full/2003/01/aah3710/img370.gif)
![]() the spectral distortion writes as
the spectral distortion writes as
![\begin{displaymath}\Delta i(x,\theta)=\frac{1}{2} \tau^2(\theta) [j_2(x)-2j_1(x)+j_0(x)],
\end{displaymath}](/articles/aa/full/2003/01/aah3710/img371.gif)
![]() ,
by the sum of the single spectral
distortions of each population
,
by the sum of the single spectral
distortions of each population