The best studied cases of microquasar activity show that large amounts of
kinetic energy can be liberated: conservative equipartition estimates of
the energy released in the major outbursts of GRS 1915+105 give
![]() (Mirabel & Rodríguez 1999; Fender et al. 1999a), released
over a period of a few days at most.
(Mirabel & Rodríguez 1999; Fender et al. 1999a), released
over a period of a few days at most.
Existing radio monitoring data (Pooley & Fender 1997; Foster et al. 1996) show that GRS
1915+105 exhibits several giant flares per year, not all of which were
observed with detailed campaigns (e.g., Fender et al. 1999a). This yields
an estimated average kinetic power, and, since almost all of the energy
will initially be deposited in the form of CRs, an estimated cosmic ray
power of
![]() for GRS 1915+105
alone. In fact, GRS 1915+105 seems to release an even higher power in the
form of microflares between major outbursts, estimated to exceed
for GRS 1915+105
alone. In fact, GRS 1915+105 seems to release an even higher power in the
form of microflares between major outbursts, estimated to exceed
![]() (Mirabel & Rodríguez 1999) and even
(Mirabel & Rodríguez 1999) and even
![]() (Fender & Pooley 2000).
(Fender & Pooley 2000).
Using the publicly available GBI monitoring data (http://www.gb.nrao.edu/fgdocs/gbi/gbint.html), we estimate that GRS
1915+105 spends in excess of 60% of its time at flux levels significantly
enhanced over the baseline flux (GBI monitoring data of Cyg X-3 show a
similar rate), with about 2 major outbursts per year (see
Fig. 6 and also Fender et al. 1999a; Foster et al. 1996). Assuming that the
observed radio flux in flares is proportional to the amount of kinetic
energy released in the flare, and using the observed 1997 flare
(Fender et al. 1999a) with a minimum kinetic energy estimate of
![]() ,
we estimate that over the period covered by GBI
monitoring, the mean kinetic luminosity of GRS 1915+105 in flares is of
order
,
we estimate that over the period covered by GBI
monitoring, the mean kinetic luminosity of GRS 1915+105 in flares is of
order
![]() .
If the baseline
radio emission from GRS 1915+105 is also due to low level jet emission,
this estimate increases by a factor
.
If the baseline
radio emission from GRS 1915+105 is also due to low level jet emission,
this estimate increases by a factor ![]() 1.4.
1.4.
| |
Figure 6: Plot of the 2.25 GHz GBI monitoring data ( http://www.gb.nrao.edu/fgdocs/gbi/gbint.html) for GRS 1915+105 over the time span from June 1994 to August 2000. Shown as a hatched area is the flux considered above the baseline flux, i.e., the flux considered to originate from flares, which we integrated to arrive at the estimate for the average kinetic power carried by the jet. The flare analyzed by Fender et al. (1999a) is indicated by the mark "F99''. The large gaps are due to gaps in the monitoring campaign and were not included in the procedure. |
The jets in SS433 are even more impressive: Reasonable estimates put the
total, continuous kinetic power in excess of
![]() -
-
![]() (Marshall et al. 2002; Margon 1984; Spencer 1984), which is already of order 1-10% of the total Galactic CR luminosity. While the jets in SS433 are only
mildly relativistic, and the production of observable, relativistic CRs
thus falls under similar restrictions with regard to particle acceleration
efficiency as supernovae, the example of SS433 does show that Galactic jets
are capable of releasing impressive amounts of kinetic energy. Thus, jets
from objects like SS433 (with mildly relativistic bulk speeds) might be an
important source of sub-CRs in the Galaxy, influencing heating and
ionization of the ISM.
(Marshall et al. 2002; Margon 1984; Spencer 1984), which is already of order 1-10% of the total Galactic CR luminosity. While the jets in SS433 are only
mildly relativistic, and the production of observable, relativistic CRs
thus falls under similar restrictions with regard to particle acceleration
efficiency as supernovae, the example of SS433 does show that Galactic jets
are capable of releasing impressive amounts of kinetic energy. Thus, jets
from objects like SS433 (with mildly relativistic bulk speeds) might be an
important source of sub-CRs in the Galaxy, influencing heating and
ionization of the ISM.
Since the subject of Galactic microquasars is still relatively young, and
many of the known sources have only been discovered in recent years,
estimating the true Galactic rate of radio outburst events and thus the
total Galactic power in relativistic jets is difficult. Taking the
interval from 1994 through 2000, there were at least 7 well observed giant
radio outbursts comparable in strength with GRS 1915+105 (corrected for
Galactic distance) in the sources Cyg X-3 (Mioduszewski et al. 2001), GRO
J1655-40 (Hjellming & Rupen 1995), GRS 1915+105 (Mirabel & Rodríguez 1994; Fender et al. 1999a),
V4641 Sgr (Orosz et al. 2001), and XTE J1748-288 (Fender & Kuulkers 2001), giving a
very conservative lower limit on the Galactic rate of
![]() .
As with GRS 1915+105, we expect many giant flares to have gone unnoticed,
and a more reasonable estimate of the event rate would be of the order of
10-100 Galactic events per year.
.
As with GRS 1915+105, we expect many giant flares to have gone unnoticed,
and a more reasonable estimate of the event rate would be of the order of
10-100 Galactic events per year.
Cyg X-3, which is believed to be relativistically beamed, shows radio peak
luminosities up to 200 times stronger than GRS 1915+105 (Fender & Kuulkers 2001),
and often exhibits flaring activity (Ogley et al. 2001) at or above the peak
level of GRS 1915+105 on timescales of ![]() 10 days. The other sources
mentioned above are very similar to each other in peak radio luminosity
(Fender & Kuulkers 2001), which we take as an indicator of kinetic power (most of
these sources are not resolved and an estimate of the equipartition energy
of the jet is thus not possible).
10 days. The other sources
mentioned above are very similar to each other in peak radio luminosity
(Fender & Kuulkers 2001), which we take as an indicator of kinetic power (most of
these sources are not resolved and an estimate of the equipartition energy
of the jet is thus not possible).
If indeed these sources operate on the same level as GRS 1915+105, the
minimum kinetic luminosity of these seven sources together would be
![]() .
Since this estimate is based on
the minimum energy estimates of
.
Since this estimate is based on
the minimum energy estimates of
![]() in GRS 1915+105, the true
kinetic luminosity of these sources might well be much larger.
in GRS 1915+105, the true
kinetic luminosity of these sources might well be much larger.
Furthermore, there are many sources that are known to have been active at earlier epochs [e.g., V404 Cyg, Han & Hjellming 1992 and Cir X-1, Haynes et al. 1978], which exhibited flux levels comparable to the above mentioned sources. Many sources currently active might simply not have been detected yet. Similarly, many more X-ray sources are observed to be consistently active at lower radio fluxes (e.g., Cyg X-1, or GX 339-4, Fender 2001) than the brightest sources mentioned above.
During the past few years, it has become clear that radio emission from Galactic X-ray sources is a very common phenomenon. Radio emission is usually detected during state changes of the X-ray source (into or out of the low/hard state), including soft X-ray transients. While the powerful radio flares discussed above are associated with such transients, there are many more X-ray sources which are active at lower radio flux levels (e.g., Cyg X-1, or GX 339-4, Fender 2001).
These sources are observed to produce stationary, optically thick jet emission (as opposed to the already optically thin emission detected in typical radio flares of transient jets). It is not clear whether these jets are in fact relativistic and how much energy they carry. One might hope to estimate the kinetic power from the observed flux, scaling it to the peak flux observed in GRS 1915 as was done above for transient sources, but detailed kinematic modeling of the jet would be required to justify such a simple argument. In any event, because no complete sample of such sources exists, it is impossible to estimate the total fraction of mechanical jet power contained in low power sources. Furthermore, these sources might have shown transient activity in the past as well, given that GRS 1915+105 also shows steady, quiescent radio emission at comparable flux levels.
Other sources like 1E 1740-294 (Mirabel et al. 1992), GRS 1758-258 (Martí et al. 1998), and Cir-X1 (Stewart et al. 1993) show permanent extended structure resembling radio lobes in extragalactic radio sources, which are witness to past radio activity and must harbor a significant amount of CRs as well. We note here that estimating the total kinetic power from the presence or absence of radio lobes in microquasar sources (indicating past activity) is severely hampered by the fact that Galactic radio lobes are expected to have very low surface brightness (Heinz 2002).
The estimate for the kinetic energy output from GRS 1915+105
(Fender et al. 1999a), which we used as a template case to estimate the total
Galactic energy in jets, is based on the assumption that the jet plasma is
composed of a powerlaw of relativistic electrons and cold protons (for
charge conservation). The electron spectrum was assumed to extend only
over the range in frequency observed in the radio. While an IR detection
of the jet indicates a high energy tail of the spectrum
(Sams et al. 1996; Mirabel et al. 1996; Eikenberry et al. 1998), a low energy component (down to
![]() )
has never been observed in any jet due to lack of
viable emission mechanisms to reveal such a component. The possibility of
detecting this component via inverse Compton scattering has been discussed,
for example, by Ensslin & Sunyaev (2001).
)
has never been observed in any jet due to lack of
viable emission mechanisms to reveal such a component. The possibility of
detecting this component via inverse Compton scattering has been discussed,
for example, by Ensslin & Sunyaev (2001).
Finally, the physical structure of microquasar jets is still not known-they could be made of either discrete ejections or a continuous stream of matter. If the jet is not composed of discrete ejections, but instead is a continuous outflow with knots corresponding to internal shocks, Kaiser et al. (2000) have shown that, in the case of GRS 1915+105, the estimate of the total kinetic energy carried in the jet (and thus the total CR energy released in the working surface) is a factor of 10 higher than the above estimate (though the instantaneous kinetic power is reduced), corrections for the low energy end of the particle distribution notwithstanding.
All of this indicates that the lower limit of
![]() is conservative, and it might be that the
kinetic luminosity from microquasars is of the order of 10% of the total
Galactic cosmic ray power
is conservative, and it might be that the
kinetic luminosity from microquasars is of the order of 10% of the total
Galactic cosmic ray power
![]() .
Clearly, the uncertainty in
frequency and power of radio flares in microquasars warrants continued
monitoring of these sources to answer the question of how important energy
input by these sources really is.
.
Clearly, the uncertainty in
frequency and power of radio flares in microquasars warrants continued
monitoring of these sources to answer the question of how important energy
input by these sources really is.
For a cold ballistically expanding ejection, most of the energy is
dissipated in the forward shock. This is implied by the small opening
angle ![]() of the ejection: as long as
of the ejection: as long as
![]() (with
(with
![]() being
the bulk Lorentz factor of the ejection), the characteristic transverse
size of the ejection R is always much smaller than the distance d over
which it slows down, as seen in the frame of the blob:
being
the bulk Lorentz factor of the ejection), the characteristic transverse
size of the ejection R is always much smaller than the distance d over
which it slows down, as seen in the frame of the blob:
![]() (here, the factor of
(here, the factor of
![]() accounts for
the Lorentz contraction in going to the frame of the ejection). Thus, the
deceleration time
accounts for
the Lorentz contraction in going to the frame of the ejection). Thus, the
deceleration time
![]() is much longer than the light
crossing time of the ejection R/c, and the deceleration must occur in a
sub-relativistic shock. This implies that the ejection is not heated to
relativistic temperatures, while the forward shock must be relativistic,
with shock velocity corresponding to
is much longer than the light
crossing time of the ejection R/c, and the deceleration must occur in a
sub-relativistic shock. This implies that the ejection is not heated to
relativistic temperatures, while the forward shock must be relativistic,
with shock velocity corresponding to
![]() .
.
The particles passing through this shock will have energies of order
![]() ,
where
,
where
![]() is the initial Lorentz factor of the
ejection (before interaction with the ISM). Because the ejection is slowed
down, particles of a spread in energies are created in the forward shock,
though the spectrum will show a sharp turnover or cutoff at energies
is the initial Lorentz factor of the
ejection (before interaction with the ISM). Because the ejection is slowed
down, particles of a spread in energies are created in the forward shock,
though the spectrum will show a sharp turnover or cutoff at energies
![]() (below this cutoff, it is
plausible that the spectrum rises with
(below this cutoff, it is
plausible that the spectrum rises with
![]() ,
see Appendix A).
,
see Appendix A).
The reverse shock is relativistic if the ratio on the left hand side of Eq. (2) is smaller than unity, the forward shock is relativistic if the ratio on the left hand side is larger than unity. For Galactic sources both cases can occur for appropriate external densities, depending on the length of the jet.
For relativistic shocks the situation is not as clear cut. Several attempts have been made to solve the problem of particle acceleration at relativistic shocks, mostly in the limit of test particle acceleration. In general, it is found that powerlaw distributions with somewhat steeper spectra than in non-relativistic shocks can be produced (Ellison & Double 2002; Achterberg et al. 2001; Kirk & Schneider 1987).
It is certain, however, that acceleration of particles in the shock must take place: Particles crossing the shock are by nature already
relativistic in the downstream rest frame, with a typical Lorentz factor of
![]() ,
the relative Lorentz factor between upstream and
downstream frames. The particle distribution leaving the shock is thus
strongly anisotropic, and essentially mono-energetic. The randomization of
this energy is then a question of the efficiency of the typical plasma
processes often assumed to be present in populations of relativistic
particles.
,
the relative Lorentz factor between upstream and
downstream frames. The particle distribution leaving the shock is thus
strongly anisotropic, and essentially mono-energetic. The randomization of
this energy is then a question of the efficiency of the typical plasma
processes often assumed to be present in populations of relativistic
particles.
The simplest assumption is that the particle momenta are simply isotropized
behind the shock. The shock acceleration kernel is then a delta function
and a cold upstream plasma will be transformed into a narrow but
relativistic energy distribution, the width
![]() of which
should roughly be given by the Lorentz transformed width
of which
should roughly be given by the Lorentz transformed width ![]() of the
upstream energy distribution,
of the
upstream energy distribution,
![]() ,
where
,
where
![]() is the relative Lorentz factor
between the upstream and downstream frames. The mean particle energy will
be
is the relative Lorentz factor
between the upstream and downstream frames. The mean particle energy will
be
![]() .
.
If scattering by downstream turbulence or particle interactions is stronger, the particles can be thermalized, in which case a Maxwell-Boltzmann distribution according to the relativistic Rankine-Hugoniot jump conditions will be established. The main observational difference between these two cases will be the width of the energy distribution (see Fig. 5).
If a significant fraction of the particles can perform multiple shock
crossings (which again hinges on effective scattering to return downstream
particles to the shock), we expect a powerlaw-type distribution to be
established. It is reasonable to assume that the first time escape
fraction from the downstream region (i.e., the probability that a particle
which crossed the shock only once) is of order
![]() (e.g., Achterberg et al. 2001), which implies that most of the
particles will only cross the shock once (note that the escape
probability in non-relativistic shocks is generally very small for fast
particles, though
(e.g., Achterberg et al. 2001), which implies that most of the
particles will only cross the shock once (note that the escape
probability in non-relativistic shocks is generally very small for fast
particles, though
![]() is of order unity for thermal
particles, Bell 1978). The escape fraction in the upstream region is much
smaller and generally neglected in calculations.
is of order unity for thermal
particles, Bell 1978). The escape fraction in the upstream region is much
smaller and generally neglected in calculations.
The particles re-crossing the shock will pick up another factor of order
![]() in energy gain (Vietri 1995), which implies that a
significant fraction of particles will be boosted to higher energies
(
in energy gain (Vietri 1995), which implies that a
significant fraction of particles will be boosted to higher energies
(
![]() ). This fraction of the particles will
contribute a significant amount of pressure to the post shock gas, which
will modify the shock structure accordingly. Thus, the amount of energy
accessible to the bulk of the particles which cross the shock only once is
of the order
). This fraction of the particles will
contribute a significant amount of pressure to the post shock gas, which
will modify the shock structure accordingly. Thus, the amount of energy
accessible to the bulk of the particles which cross the shock only once is
of the order
![]() .
.
The remaining fraction
![]() of the particles will perform
true Fermi acceleration. The low energy turnover of this distribution
should be located roughly at
of the particles will perform
true Fermi acceleration. The low energy turnover of this distribution
should be located roughly at
![]() (Vietri 1995) and subsequent shock crossings will produce features
at energies of
(Vietri 1995) and subsequent shock crossings will produce features
at energies of
![]() (where i enumerates the number
of shock crossings). The similarity of this process to Compton
upscattering was already mentioned in Sect. 2.3.
(where i enumerates the number
of shock crossings). The similarity of this process to Compton
upscattering was already mentioned in Sect. 2.3.
The superposition of features from multiple shock crossing cycles will lead
to the formation of a powerlaw at high energies, very similar to the
powerlaw produced by optically thin inverse Compton scattering (where the
Lorentz transformations of the photon distribution to and from the particle
rest frame are replaced by Lorentz transformations to and from the upstream
fluid rest frame, assuming that scattering is strong enough to isotropize
the particle distribution. The optical depth
![]() is replaced
by the return probability
is replaced
by the return probability
![]() .) The shock powerlaw slope
.) The shock powerlaw slope
![]() is determined by
is determined by
![]() and
and
![]() (e.g., Bell 1978):
(e.g., Bell 1978):
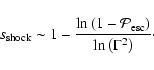 |
(4) |
We note that Achterberg et al. (2001) argue that in the absence of an
efficient scattering mechanism, the average energy gain per particle will
be restricted to a factor of order unity (rather than
![]() )
for higher order shock crossings (
)
for higher order shock crossings (![]() ), and that the low energy
turnover of the powerlaw component might thus be located at
), and that the low energy
turnover of the powerlaw component might thus be located at ![]()
![]() (rather than
(rather than
![]() ). The search for
additional features in the CR spectrum at energies
). The search for
additional features in the CR spectrum at energies ![]() and
and
![]() might offer a potential way to test these predictions.
might offer a potential way to test these predictions.
It is also possible that a population of relativistic protons already
exists upstream of the shock. If the proton number density is equal to the
electron number density, the bulk of the particles and of the energy will
presumably be at the low energy end (
![]() ), otherwise the
estimates for kinetic energy flux in the jet would have to be increased
accordingly, increasing the impact on the Galactic CR spectrum as well (by
a factor of
), otherwise the
estimates for kinetic energy flux in the jet would have to be increased
accordingly, increasing the impact on the Galactic CR spectrum as well (by
a factor of ![]() ,
the low energy cutoff of the distribution).
,
the low energy cutoff of the distribution).
This population will be shifted to higher energies in the shock, and
possibly experience further Fermi type acceleration. Thus, if a powerlaw
of relativistic protons exists prior to the terminal shock with lower
cutoff
![]() and spectral index
and spectral index
![]() ,
the terminal shock
should shift the lower cutoff roughly to
,
the terminal shock
should shift the lower cutoff roughly to
![]() ,
while the slope of the new powerlaw will be
,
while the slope of the new powerlaw will be
![]() ,
where
,
where
![]() is the powerlaw slope produced in the
relativistic terminal shock.
is the powerlaw slope produced in the
relativistic terminal shock.
While the particles produced in the shock must be relativistic at injection, the dynamical evolution of the shocked gas can reduce their energies significantly if adiabatic cooling is important before the particles can escape the shock region (radiative cooling of the nucleon distribution will be negligible). The diffusion of particles out of radio lobes and hot spots is a highly uncertain process and has not been studied in the necessary detail to answer this important question. Rather than discussing it at length, which would by far exceed the scope of this paper, we decided to include a short discussion in Appendix B, where we show that adiabatic losses do indeed pose a significant obstacle to particle escape (see also Fig. 5).
The spectral index of the non-thermal emission from the lobes of 1E
1740-294 is
![]() (Mirabel et al. 1992), corresponding to an
electron spectrum of slope of
(Mirabel et al. 1992), corresponding to an
electron spectrum of slope of
![]() .
If the protons are
injected at the working surface with the same slope (this would require
that the electron spectrum is unaffected by radiative cooling and that the
powerlaw electrons are not just advected through the shock from upstream),
then the observed CR slope near the earth should be steepened by
.
If the protons are
injected at the working surface with the same slope (this would require
that the electron spectrum is unaffected by radiative cooling and that the
powerlaw electrons are not just advected through the shock from upstream),
then the observed CR slope near the earth should be steepened by
![]() due to the energy dependence in the Galactic diffusion coefficient.
This would yield a proton powerlaw slope of
due to the energy dependence in the Galactic diffusion coefficient.
This would yield a proton powerlaw slope of
![]() ,
somewhat
steeper than the canonical CR slope of
,
somewhat
steeper than the canonical CR slope of
![]() ,
though not
significantly.
,
though not
significantly.
Part of the observed powerlaw electron distribution inside the tentative
radio lobes of 1E 1740-294 and GRS 1758-258 could also have been advected
from the jet. In fact, is is unclear whether electrons can be accelerated
efficiently in a shock if protons are present, since the shock thickness
will be set by the proton Larmor radius, which will be much larger than the
electron Larmor radius (e.g., Achterberg et al. 2001). In this case, the
electrons will not experience a shock at all, more likely, they will be
accelerated adiabatically to a narrow component with energies of order
![]() .
Such a component will not be
detectable through synchrotron radiation.
.
Such a component will not be
detectable through synchrotron radiation.
A detailed model of the energetic history of the particles in the lobes of 1E 1749-294 would be required to answer these questions.
Copyright ESO 2002