It is straight forward to calculate the particle distribution produced by
single pass shock acceleration in a decelerating ejection in the
ultra-relativistic limit, assuming that one has knowledge of the single pass
shock acceleration kernel at a given shock velocity
![]() .
.
Take an ejection of initial mass M0 and Lorentz factor ![]() ,
which
is sweeping up and shocking external matter. The total energy of the
ejection and the swept up matter is
,
which
is sweeping up and shocking external matter. The total energy of the
ejection and the swept up matter is
Since E is conserved, we can take the derivative of Eq. (A.1)
with respect to ![]() ,
and arrive at
,
and arrive at
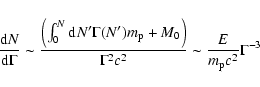 |
(A.2) |
To arrive at the observed particle distribution
![]() ,
this must be
convolved with the single shock acceleration kernel
,
this must be
convolved with the single shock acceleration kernel
![]() ,
however, for a narrow kernel, such as assumed in this paper, the powerlaw
approximation seems sufficient:
,
however, for a narrow kernel, such as assumed in this paper, the powerlaw
approximation seems sufficient:
![]() .
.
Copyright ESO 2002