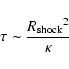 |
(B.1) |
An important question is whether the particles produced in the shock discussed in Sect. 3.3.1 can indeed diffuse out of the shock region, in which case they will freely escape and propagate through the Galaxy essentially with the energy obtained in the shock, or whether they are trapped inside the shocked gas until it expands adiabatically after the shock has passed and activity has ceased. In the latter case, the particles will lose a significant amount of energy to adiabatic expansion.
Following the discussion in Sect. 3.3.1, we distinguish two cases: dissipation in the forward and in the reverse shock.
The escape time of the particles out of the shock can be estimated as
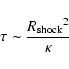 |
(B.1) |
While the shocked ISM must still be magnetically connected with the
unshocked ISM, the jet plasma will be situated on field lines advected out
from the central engine, which are likely not connected with the ISM. In
the forward shock, the relevant diffusion coefficient should then be taken
as
![]() ,
the diffusion
coefficient parallel to the mean magnetic field, while for the reverse
shock one has to consider diffusion across the magnetic boundary of the
contact discontinuity between shocked jet plasma and shocked ISM in
addition to diffusion to the contact discontinuity and away from it.
,
the diffusion
coefficient parallel to the mean magnetic field, while for the reverse
shock one has to consider diffusion across the magnetic boundary of the
contact discontinuity between shocked jet plasma and shocked ISM in
addition to diffusion to the contact discontinuity and away from it.
A lower limit on the diffusion time out of the shock is thus given by the value for the forward shock, since the particles which have diffused out of the reverse shock must, in addition, also propagate through the forward shock.
Using the simple approximate expression for
![]() (e.g., Kennel & Petschek 1966), and assuming a Kolmogorov turbulence spectrum
for the magnetic field originating on scales of order the shock size
(e.g., Kennel & Petschek 1966), and assuming a Kolmogorov turbulence spectrum
for the magnetic field originating on scales of order the shock size
![]() and containing a fraction
and containing a fraction
![]() of the total magnetic energy, the parallel diffusion coefficient
for a particle with energy
of the total magnetic energy, the parallel diffusion coefficient
for a particle with energy
![]() can be written as
can be written as
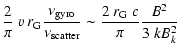 |
|||
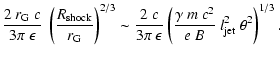 |
(B.2) |
Writing the shock area as
![]() gives an approximate hot
spot pressure
gives an approximate hot
spot pressure
![]() of
of
The comoving (i.e., measured in the frame of the shocked plasma)
limit to the proton escape time
![]() is then
is then
If the turbulent velocity inside the region of interest is comparable to
the expansion velocity, and if large scale turbulence is present (which was
the underlying assumption in out estimate of ![]() above), then
turbulent transport could aid particle escape: in a simple mixing length
approach, the diffusion coefficient can be approximated by
above), then
turbulent transport could aid particle escape: in a simple mixing length
approach, the diffusion coefficient can be approximated by
![]() ,
where
,
where
![]() is the
characteristic turbulent velocity and
is the
characteristic turbulent velocity and
![]() the scale length of
the largest scale turbulence. The turbulent transport time is then
the scale length of
the largest scale turbulence. The turbulent transport time is then
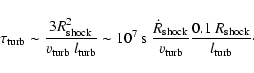 |
(B.5) |
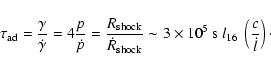 |
(B.6) |
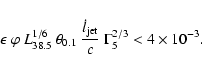 |
(B.7) |
 |
(B.8) |
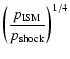 |
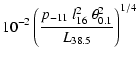 |
(B.9) | |
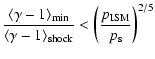 |
|||
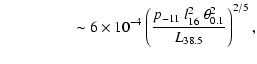 |
In jets where dissipation occurs mainly in the reverse shock, the jet geometry is similar to AGN jets (i.e., the jets are effectively reflected by the ISM, thus inflating a cocoon with spent jet fuel).
Particles accelerated in the shock will eventually be advected out of the
shock region and into the cocoon (see Fig. 2). The
timescale for this process is
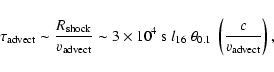 |
(B.10) |
The diffusion time towards the contact discontinuity is given by
Eq. (B.4). In order to enter the forward shock, the particules
have to propagate across the magnetic boundary at the contact
discontinuity, which introduces an additional cross-field diffusion term.
The contact discontinuity will have a typical thickness of the order of the
Larmor radius ![]() of the particles, thus the particles will have to
traverse a region of size
of the particles, thus the particles will have to
traverse a region of size ![]() perpendicular to the field in order
to cross the contact discontinuity (this approximation is valid as long as
the parallel diffusion time over one coherence length of the field is
longer than the perpendicular diffusion time across one Larmor radius,
otherwise the perpendicular diffusion time across one coherence length
should be used). The lower limit to the diffusion time across the field is
then
perpendicular to the field in order
to cross the contact discontinuity (this approximation is valid as long as
the parallel diffusion time over one coherence length of the field is
longer than the perpendicular diffusion time across one Larmor radius,
otherwise the perpendicular diffusion time across one coherence length
should be used). The lower limit to the diffusion time across the field is
then
![]() .
.
The perpendicular diffusion coefficient
![]() can be
approximated as
can be
approximated as
![]() (e.g., Parker 1965), i.e.,
(e.g., Parker 1965), i.e.,
Thus, it is rather likely that the bulk of the particles are advected out
of the shock and into the cocoon. The pressure driven expansion of a
cocoon can be approximated by a simple spherically symmetric model:
Dimensional analysis suggests that the size of the cocoon ![]() follows a simple scaling (Castor et al. 1975)
follows a simple scaling (Castor et al. 1975)
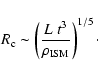 |
(B.12) |
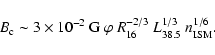 |
(B.14) |
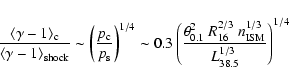 |
(B.15) |
Once the particles are inside the cocoon, the escape time is again given by
![]() with the expressions for
with the expressions for
![]() and
and
![]() from Eqs. (B.4)
and (B.11), though with different values:
from Eqs. (B.4)
and (B.11), though with different values:
![\begin{displaymath}\tau_{\parallel} \sim 7\times 10^{8}~{\rm
s}~R_{16}~\left[\e...
...{1/9}~\Gamma^{-1/3}~ L_{38.5}^{1/9}~n_{\rm
ISM}^{1/18}\right]
\end{displaymath}](/articles/aa/full/2002/29/aah3163/img271.gif) |
(B.16) |
![\begin{displaymath}\tau_{\perp} \sim 4.5\times 10^{3}~{\rm
s}~R_{16}~\left[\eps...
...\Gamma^{-1/3}~ L_{38.5}^{1/9}~n_{\rm
ISM}^{1/18}\right]^{-1}.
\end{displaymath}](/articles/aa/full/2002/29/aah3163/img272.gif) |
(B.17) |
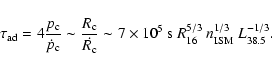 |
(B.18) |
Copyright ESO 2002