In this section we will present a general description of the model proposed for CR production in microquasars.
As we will argue below, it is likely that the plasma traveling far
downstream in the jet towards the working surface is cold (the mean
particle velocity is
![]() in the rest frame of the
jet plasma), especially if microquasar jets are composed of electron-ion
plasma. The same is, of course, also true for the undisturbed interstellar
medium (ISM). Thus, the bulk of the plasma transported to the interface
between the jet and the ISM (for simplicity we will call this interface the
working surface of the jet, regardless of its detailed physical structure)
is initially cold.
in the rest frame of the
jet plasma), especially if microquasar jets are composed of electron-ion
plasma. The same is, of course, also true for the undisturbed interstellar
medium (ISM). Thus, the bulk of the plasma transported to the interface
between the jet and the ISM (for simplicity we will call this interface the
working surface of the jet, regardless of its detailed physical structure)
is initially cold.
This conjecture is inspired by observations of the mildly relativistic jets
in SS433 (the best studied relativistic Galactic jet to date, albeit mildly
relativistic and not considered a microquasar). In this source, red- and
blue-shifted Balmer H![]() and other optical recombination lines, usually
radiated by plasmas with temperatures of order
and other optical recombination lines, usually
radiated by plasmas with temperatures of order
![]() ,
allow the determination of the bulk velocity of the flow:
0.26 c. This velocity is remarkably constant over the 20 years the
source has been observed (Margon 1984; Milgrom et al. 1982). ASCA
(Kotani et al. 1998) and recent Chandra (Marshall et al. 2002) observations
of X-ray lines of hydrogen- and helium-like ions of iron, Argon, Sulfur,
and Oxygen show that these ions are moving in the flow with the same
velocity, 0.26 c. This X-ray emitting plasma at temperatures of
,
allow the determination of the bulk velocity of the flow:
0.26 c. This velocity is remarkably constant over the 20 years the
source has been observed (Margon 1984; Milgrom et al. 1982). ASCA
(Kotani et al. 1998) and recent Chandra (Marshall et al. 2002) observations
of X-ray lines of hydrogen- and helium-like ions of iron, Argon, Sulfur,
and Oxygen show that these ions are moving in the flow with the same
velocity, 0.26 c. This X-ray emitting plasma at temperatures of
![]() is observed at
much smaller distances (
is observed at
much smaller distances (![]()
![]() )
from the central compact
object than the optical line emission region (
)
from the central compact
object than the optical line emission region (![]()
![]() ). A
striking feature of the SS433 jet is that the plasma is observed to be
moving with relativistic velocities. Yet, at the same time the jet plasma
itself shows very little line broadening (i.e., it is cold).
). A
striking feature of the SS433 jet is that the plasma is observed to be
moving with relativistic velocities. Yet, at the same time the jet plasma
itself shows very little line broadening (i.e., it is cold).
If microquasar jets are similar to the SS433 jets in composition and
properties (i.e., cold electron-ion plasma at relativistic bulk speeds) the
consequences for the interpretation of these jets will be far reaching, as
we will argue below. Independent from this argument, the radio synchrotron
emission detected from microquasar jets and several radio nebulae
surrounding microquasar sources (see Sect. 3.1) is clear
evidence for the presence of relativistic electrons, which, when released
into the ISM, will act as cosmic ray electrons.
The standard picture for the interface between powerful radio galaxies and
their environment is a strong double shock structure (forward shock into
the ISM and reverse shock into the jet), shown in Fig. 2.
The shocked jet material is shed at the head of the jet and inflates an
enshrouding cocoon around the jet, filled with relativistic plasma, which
has gone through the terminal shock. Such a scenario might also be
relevant for the terminus of Galactic relativistic jets. A similar picture
arises if the jets are composed of discrete ejections, propagating into an
external medium at relativistic speeds, as sketched in
Fig. 3.
 |
Figure 3:
Left: cartoon of a jet composed of discrete ejections with
precession. In such a non-stationary picture, each ejection is slowed by
its interaction with the ISM (which might be disturbed by previous
ejections). This interaction will likely happen in the form of a forward
shock (into the ISM). ISM particles will leave the shock with energies of
order
|
A cold upstream particle crossing an ultra-relativistic shock into a
downstream region with relative Lorentz factor
![]() will have an internal energy of
will have an internal energy of
![]() in the downstream frame after the first shock
crossing. Consequently, all initially cold particles will leave the shock
with about the same specific energy
in the downstream frame after the first shock
crossing. Consequently, all initially cold particles will leave the shock
with about the same specific energy
![]() .
Particles can
pick up additional energy if they cross the shock multiple times, which is
the basis of diffusive shock acceleration schemes like Fermi acceleration,
resulting in the formation of a powerlaw distribution. However, as has
recently been shown by Achterberg et al. (2001), the bulk of the particles
crossing a relativistic shock escape after the very first shock passage and
will therefore not participate in diffusive shock acceleration. It is
these particles that carry off the bulk of the dissipated jet energy.
.
Particles can
pick up additional energy if they cross the shock multiple times, which is
the basis of diffusive shock acceleration schemes like Fermi acceleration,
resulting in the formation of a powerlaw distribution. However, as has
recently been shown by Achterberg et al. (2001), the bulk of the particles
crossing a relativistic shock escape after the very first shock passage and
will therefore not participate in diffusive shock acceleration. It is
these particles that carry off the bulk of the dissipated jet energy.
As a result, the bulk of the particles might leave the shock with a narrow
energy distribution, peaking at an energy close to the specific kinetic
energy of the jet:
![]() ,
with an energy width similar to or higher than the Lorentz
transformed thermal velocity,
,
with an energy width similar to or higher than the Lorentz
transformed thermal velocity,
![]() (i.e., very narrow, since the internal sound speed
(i.e., very narrow, since the internal sound speed ![]() is small:
is small:
![]() ).
).
Whether this narrow distribution will be preserved as the particles travel
away from the shock, or whether it will be thermalized, depends on the
efficiency of collective plasma effects and small angle scattering on
magnetic field irregularities, which are also needed to isotropize the
particle distribution. If collective effects are strong, the particle
spectrum will be broadened into a relativistic Maxwell-Boltzmann
distribution, with a temperature corresponding to the value given by the
relativistic Rankine-Hugoniot jump conditions. In the case of a strong,
ultra-relativistic shock, this is simply
![]() ,
i.e., the mean particle energy is just
,
i.e., the mean particle energy is just
![]() (e.g. Blandford & McKee 1976). In this case the relativistic proton plasma
in the shocked ISM is equivalent to the X-ray emitting gas in SNR shocks.
However, in microquasar shocks we have extremely rarefied, relativistic
particles with a relatively narrow thermal (i.e., not powerlaw) energy
distribution.
(e.g. Blandford & McKee 1976). In this case the relativistic proton plasma
in the shocked ISM is equivalent to the X-ray emitting gas in SNR shocks.
However, in microquasar shocks we have extremely rarefied, relativistic
particles with a relatively narrow thermal (i.e., not powerlaw) energy
distribution.
However, the structure of relativistic shocks is still not well understood
and it might be that this interface is not a simple double shock structure.
It could be significantly different in nature. For example, the jet could
be magnetically connected with the environment, i.e., if the flux tubes
join smoothly with the large scale magnetic field of the ISM, as shown in
the cartoon in Fig. 4 (note, however, that
Lubow et al. 1994 showed that realizing such configuration is rather
difficult).
In such a case the shock would be replaced by stochastic pitch angle
scattering of the particle distribution (this can occur if the jet is
moving sub-Alfv
![]() nically, for example). Since the jet plasma
is traveling relative to the ISM, such a scenario would excite strong
two-stream instabilities at the interface between ISM and jet plasma, which
would isotropize and possibly thermalize the particle distribution of the
jet very quickly. The deposition of jet thrust would then imply that this
interface is itself moving through space. Precession, as observed in SS433
(e.g., Milgrom 1979) and suggested to be present in GRO 1655-40
(Hjellming & Rupen 1995), will significantly alter the dynamical balance
between ISM and jet plasma, as will the time dependent nature of the
interface if the jets are composed of discrete ejections.
nically, for example). Since the jet plasma
is traveling relative to the ISM, such a scenario would excite strong
two-stream instabilities at the interface between ISM and jet plasma, which
would isotropize and possibly thermalize the particle distribution of the
jet very quickly. The deposition of jet thrust would then imply that this
interface is itself moving through space. Precession, as observed in SS433
(e.g., Milgrom 1979) and suggested to be present in GRO 1655-40
(Hjellming & Rupen 1995), will significantly alter the dynamical balance
between ISM and jet plasma, as will the time dependent nature of the
interface if the jets are composed of discrete ejections.
If furthermore the magnetic field is stochastically tangled on small scales, the detailed behavior of the plasma could be very complicated, with a gradual change from relativistic, ballistic motion to random propagation. Qualitatively, this would be comparable to extragalactic FR I sources (though the exact nature of the dynamics in FR I sources is not yet clear, either).
In such a case, the absence of a strong shock would preclude diffusive
shock acceleration (though stochastic acceleration might still exist if
particles scatter off of relativistic turbulence which might exist in the
transition region between jet and ISM). Only the narrow or thermalized
component with mean energy of
![]() and strong
cutoff at higher energies would exist.
and strong
cutoff at higher energies would exist.
Even if most of the particles are thermalized downstream, the spectrum will
still show a steep turnover beyond energies of order
![]() (see the dashed curve in Fig. 5),
which will appear as an edge-like feature in the overall CR spectrum.
(see the dashed curve in Fig. 5),
which will appear as an edge-like feature in the overall CR spectrum.
Similarly, a number of other processes will tend to broaden any narrow
component produced in the working surface, including adiabatic losses
(competing with diffusion of particles out of the loss region, see Appendix
B and the right panel in Fig. 5) and
solar modulation. The effect of these processes will be to spread
particles to lower energies, leaving the strong turnover/cutoff above
energies of
![]() intact.
intact.
The only serious cooling these CR protons at energies of a few GeV might experience will be adiabatic losses, which will occur if the particles are confined to an expanding plasma volume (e.g., if it is overpressured with respect to the environment). However, since many processes can lead to increased diffusion of these particles, it appears plausible that a large fraction of the CRs might escape before they suffer strong adiabatic losses.
If a component of cold electrons is also present in the jets in addition to
the observed powerlaw electrons, a similar, very low energy
relativistic electron component (around 2-5 MeV) might appear. However,
it would contain only a fraction
![]() of the energy in the
proton component.
of the energy in the
proton component.
The remaining fraction of particles (both ions and electrons) which do not escape the shock after the first shock passage and thus perform multiple shock crossings will be accelerated diffusively to a powerlaw-like distribution. Only the high energy tail of this powerlaw-like electron component is directly observable via synchrotron radio emission.
Likening the acceleration of particles crossing a relativistic shock to the
problem of Compton up-scattering of low energy photons on relativistic
thermal electrons (see, for example, Pozdnyakov et al. 1983), we note that
a particle scattered both up-stream and down-stream of the shock will
experience an energy gain by a factor of order
![]() per
crossing cycle, where
per
crossing cycle, where
![]() is the relative Lorentz factor between upstream and downstream
plasma. This was argued by Vietri (1995), applied to the acceleration
of particles in gamma-ray burst shocks. This will lead to the production
of several peaks in the spectrum. The input spectrum for this
up-scattering process is the narrow particle population produced in the
initial shock crossing (discussed above), and thus peaks will appear at
energies
is the relative Lorentz factor between upstream and downstream
plasma. This was argued by Vietri (1995), applied to the acceleration
of particles in gamma-ray burst shocks. This will lead to the production
of several peaks in the spectrum. The input spectrum for this
up-scattering process is the narrow particle population produced in the
initial shock crossing (discussed above), and thus peaks will appear at
energies ![]()
![]() ,
where i is the number of shock crossing cycles performed by the particle.
The normalization of each peak, and thus the approximate powerlaw index, is
determined by the escape probability of the particles (similar to the
optical depth in inverse Compton scattering). The resulting spectrum is
sketched in Fig. 5.
,
where i is the number of shock crossing cycles performed by the particle.
The normalization of each peak, and thus the approximate powerlaw index, is
determined by the escape probability of the particles (similar to the
optical depth in inverse Compton scattering). The resulting spectrum is
sketched in Fig. 5.
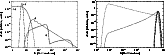 |
Figure 5:
Left panel: sketch of the predicted contribution from a
microquasar to the Galactic CR spectrum for
|
Note, however, that Achterberg et al. (2001) argue that higher order shock
crossings do not lead to energy gains of order
![]() .
In
their treatment, scattering is limited to very small angles and the energy
gain is only of order unity, and thus the position of the peaks would be
much more closely spaced, resembling a powerlaw much more than in the
Compton scattering analogy discussed in the previous paragraph. The low
energy turnover (or cutoff) of this powerlaw distribution would then be
located roughly at
.
In
their treatment, scattering is limited to very small angles and the energy
gain is only of order unity, and thus the position of the peaks would be
much more closely spaced, resembling a powerlaw much more than in the
Compton scattering analogy discussed in the previous paragraph. The low
energy turnover (or cutoff) of this powerlaw distribution would then be
located roughly at
![]() GeV. At higher
energies, multiple scattering will form a powerlaw with index
GeV. At higher
energies, multiple scattering will form a powerlaw with index![]()
![]() .
According to this simple approach, the difference between
these two pictures is therefore the energy of the second peak (
.
According to this simple approach, the difference between
these two pictures is therefore the energy of the second peak (
![]() vs.
vs.
![]() ).
).
Since the structure of relativistic shocks, and their presence in the working surfaces of microquasar jets are subject to considerable uncertainty, the observational discovery of any of the features discussed in this paper (and in particular the second peak, which would help to distinguish between the two scenarios of diffusive acceleration mentioned in the previous paragraphs, see Fig. 5) or evidence of their absence would be important input into theories of relativistic shocks.
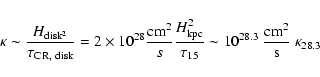 |
(1) |
There is no doubt that in the vicinity of an active microquasar the low energy part of the Galactic CR spectrum must be strongly distorted. As a result, smooth maxima or edge-like features should exist in the few GeV range of the CR spectrum. For a distant observer, the signals from several sources will be superimposed due to the long diffusion time through the galaxy. Integrally, though, deviations from the powerlaw spectrum expected in diffusive shock acceleration models should be observable.
Energy estimates which we present below show that this CR component produced in microquasars might contribute measurably to the spectrum of the CR protons in the energy band mentioned above. We will argue that, globally, microquasars should contribute upward of 0.1% of the total Galactic CR power. However, the locally measured (i.e., near earth) relative strength of the proposed CR components produced in microquasars compared to the canonical CR powerlaw distribution is highly uncertain, as it depends on the history of microquasar activity in our Galactic neighborhood.
Given these uncertainties, it might be rather difficult to detect the tiny deviations in the CR spectrum caused by distant microquasars (further complicated by the strong effects of solar modulation at and below the predicted energy range). However, they might be measurable by the upcoming AMS 02 experiment (e.g. Barrau 2001), which will offer unprecedented sensitivity and will be launched during the upcoming solar minimum (reducing the effects of solar modulation significantly). Traces of such a component might also be present in already existing high quality data sets from past or ongoing experiments, such as IMAX (Menn et al. 2000) or CAPRICE (Boezio et al. 1999).
Absence of any traces of spectral deviations in the upcoming AMS 02 experiment might become a strong argument in favor of electron-positron jets in Galactic superluminal radio sources or, alternatively, it would demonstrate that there is an unknown acceleration mechanism with 100% efficiency of transforming of the mechanical beam energy into a relativistic powerlaw distribution. Given these premises, we can state that one of the following two statements must hold: 1) either an additional hadronic CR component exists (though it may be so weak that detection inside the solar system is impossible) or 2) all jets are electron-positron dominated (in which case an additional CR electron-positron component should exist).
These abundance anomalies in GRO J1655-40 and V4641 Sgr could be the result of mass exchange between two rapidly evolving massive stars or enrichment of the normal stellar atmosphere during the supernova explosion of the primary predecessor. Accretion brings these abundance anomalies into the jet creation region in the inner disk, from where they could be transported out by the jet, eventually producing CRs by the mechanism outlined above. Similarly, Cyg X-3 is known to have an extremely hydrogen deficient Wolf-Rayet companion (van Kerkwijk et al. 1992; van Kerkwijk et al. 1996; Fender et al. 1999b), which could also lead to a large overabundance in helium and heavier elements relative to hydrogen in the produced CR spectrum.
Therefore, Galactic jets might be responsible for part of the observed CR abundance anomalies. Moreover, the CR component produced in relativistic jet sources inside the Galaxy might show rather unusual chemical abundances, in comparison with the bulk of the CRs in the powerlaw population. This would immediately distinguish Galactic jets from other CR creation mechanisms. The comparison between the measured abundances in the energy range where we expect Galactic jet sources to contribute (of order a few GeV) with those measured in the pure powerlaw regime will thus be an important probe to search for the proposed CR component. Note that the CRs produced in SNRs originate in the external shock of the swept up ISM, thus the abundances of the produced CR spectrum reflect the ISM, which might have been enriched by a pre-collapse wind, but will not show the peculiar abundance of the SN ejecta. Because all the spectral components accelerated in microquasars originate from the same plasma, they should all show the same abundance pattern. This could be a way to associate spectral features at different CR energies with a microquasar origin.
A second way to distinguish particles accelerated in the relativistic shocks of Galactic microquasars from those accelerated in non-relativistic SNR shocks is the different energy-particle mass relation: All particles in relativistic cold jets have the same Lorentz factors. Since single-pass shock acceleration will accelerate all particles to roughly the same random Lorentz factor, the peak energy for different species will be proportional to their rest mass (i.e., a fixed energy per nucleon). Electromagnetic acceleration processes would instead produce particle energies proportional to Z/A. This difference might again be measurable by AMS 02, and might already be present in CR data on heavy nuclei from experiments like HEAO-3 (Engelmann et al. 1990) or ACE (Binns et al. 2001).
Copyright ESO 2002