We have used the above formalism to estimate
eccentricity excitation/damping rates for protoplanets in eccentric
discs which can be described using the normal modes calculated above.
Before giving details we give a brief summary of our results.
Although we consider eccentricities which may substantially
exceed H/r, we shall still suppose them sufficiently small
![]() that we may consider there to be an equilibrium eccentricity
as a function of disc radius. Then a torque calculation
is characterized by a disc eccentricity, e, and an equilibrium eccentricity
which we may also consider to be the protoplanet eccentricity
that we may consider there to be an equilibrium eccentricity
as a function of disc radius. Then a torque calculation
is characterized by a disc eccentricity, e, and an equilibrium eccentricity
which we may also consider to be the protoplanet eccentricity
![]() We shall also for the most part
restrict consideration to the case
when the protoplanet and disc orbits are aligned in equilibrium
We shall also for the most part
restrict consideration to the case
when the protoplanet and disc orbits are aligned in equilibrium
![]() .
In general when
.
In general when
![]() we find
excitation of the protoplanet orbit eccentricity,
we find
excitation of the protoplanet orbit eccentricity,
![]() while for
while for
![]() the eccentricity damps as expected,
the eccentricity damps as expected,
![]() The transition between these regimes
occurs when e and
The transition between these regimes
occurs when e and ![]() are approximately equal.
For
are approximately equal.
For ![]() significantly larger than e,
provided
significantly larger than e,
provided
![]() is significantly greater than unity,
there is an equilibrium solution with apsidal line slightly rotated
from zero. The orbit may then suffer significantly reduced
or even reversed torques for
is significantly greater than unity,
there is an equilibrium solution with apsidal line slightly rotated
from zero. The orbit may then suffer significantly reduced
or even reversed torques for ![]() sufficiently large.
sufficiently large.
When ![]() is significantly less than a sufficiently
large disc eccentricity e,
the protoplanet orbital eccentricity can grow
until the orbit ceases to be aligned with the disc
and precesses through a full
is significantly less than a sufficiently
large disc eccentricity e,
the protoplanet orbital eccentricity can grow
until the orbit ceases to be aligned with the disc
and precesses through a full ![]() cycle
at which point it then damps.
Again inward orbital migration may be reduced or reversed.
Many of these features can be traced to the fact that when the
equilibrium eccentricity is such that
cycle
at which point it then damps.
Again inward orbital migration may be reduced or reversed.
Many of these features can be traced to the fact that when the
equilibrium eccentricity is such that
![]() the situation in many ways replaces the equilibrium eccentricity
solution
the situation in many ways replaces the equilibrium eccentricity
solution
![]() in an axisymmetric disc. This we show below
in an axisymmetric disc. This we show below
We use the expressions for
![]() and
and ![]() given by Eqs. (37), (39)
in the forcing potential (38).
In the case when
given by Eqs. (37), (39)
in the forcing potential (38).
In the case when
![]() and the protoplanet
orbit is almost aligned with the disc with very small
and the protoplanet
orbit is almost aligned with the disc with very small ![]() the strongest interaction occurs when
r=R, and
the strongest interaction occurs when
r=R, and
![]() This corresponds to
This corresponds to
![]() and
and
![]() Performing a first order
Taylor expansion about the point of maximum interaction
the forcing potential becomes
Performing a first order
Taylor expansion about the point of maximum interaction
the forcing potential becomes
We have calculated
![]() and
and
![]() by summing
the contributions from appropriate resonances. The normalizing
factor
by summing
the contributions from appropriate resonances. The normalizing
factor
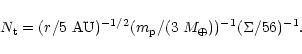
We plot ![]() for
for
![]() in
Fig. 13. The trends in all cases are similar
and are that for small
in
Fig. 13. The trends in all cases are similar
and are that for small
![]() the protoplanet eccentricity grows in the aligned case
while inward migration occurs with
the protoplanet eccentricity grows in the aligned case
while inward migration occurs with
![]() yr.
The eccentricity growth reverses for
yr.
The eccentricity growth reverses for
![]() indicating
an equilibrium in accordance with the discussion above.
We comment that for very small
indicating
an equilibrium in accordance with the discussion above.
We comment that for very small ![]() and finite e,
and finite e,
![]() For larger
For larger
![]()
![]() and
and ![]() increase and
increase and ![]() eventually changes sign for
eventually changes sign for ![]() exceeding
exceeding ![]() 0.1.
At these eccentricities
0.1.
At these eccentricities
![]() yr.
We make the comment that
the same dimensionless units can be used
for
yr.
We make the comment that
the same dimensionless units can be used
for ![]() and
and ![]() as for the disc models introduced in Sect. 2 and thus the same scaling to make results
applicable to different radii may be used.
as for the disc models introduced in Sect. 2 and thus the same scaling to make results
applicable to different radii may be used.
In the antialigned case the disc protoplanet interaction
is much weaker (see Figs. 12 and 13).
Note too that the interaction with the disc weakens in general
for larger ![]() because of the larger relative velocity
of the protoplanet with respect to the disc.
This results in larger values of
because of the larger relative velocity
of the protoplanet with respect to the disc.
This results in larger values of
![]() and
and
![]() Additional calculations have shown that, as expected, these values
become independent of the orientation of the apsidal
line when
Additional calculations have shown that, as expected, these values
become independent of the orientation of the apsidal
line when
![]()
Thus the indications are that for modest eccentricities exceeding a few H/r for both disc and protoplanet the tidal interaction may differ significantly from the circular disc and small protoplanet eccentricity case. We now consider applications to the normal modes calculated in this paper.
The equilibrium protoplanet eccentricities associated with the two highest frequency modes calculated in the case of disc model A with two interior protoplanets are shown in Fig. 2 while those corresponding to disc model B are illustrated in Fig. 3. These modes are associated with significant internal protoplanet eccentricities and can be thought of as giving the disc response to external forcing. Equilibrium eccentricities corresponding to the normal modes are also plotted in Figs. 2 and 3. These are generally larger than the disc eccentricities in the inner parts of the disc.
Equilibrium protoplanet eccentricities associated with the modes calculated in the case of disc model A with one interior protoplanet are shown in Fig. 8 while those corresponding to disc model B are illustrated in Fig. 9. Equilibrium eccentricities in the case of isolated disc model A are plotted in Fig. 10 while those corresponding to disc model B are given in Fig. 11. In all of these cases the form of the equilibrium eccentricity curve tracks that of the corresponding normal mode according to increasing number of nodes. Thus the mode with the largest number of nodes has associated equilibrium eccentricity with the largest number of nodes.
By comparing the equilibrium eccentricities with their corresponding normal modes one sees that the modes with the smallest frequencies or pattern speeds in absolute magnitude tend to have high equilibrium eccentricities several times larger than the disc eccentricity. These correspond to the longest wavelength curves in Figs. 8 and 10 with corresponding modes plotted in Figs. 4 and 6. From our discussion above these are expected to facilitate high embedded protoplanet eccentricities. The reason the protoplanet eccentricity is significantly larger than the disc eccentricity for these modes is that, for the disc mode the effects of the nonaxisymmetric forces due to self-gravity and pressure which drive the eccentricity (see Eq. (18)) tend to cancel. However, the protoplanet is subject only to self-gravity with no cancelling effects from pressure forces. Therefore the equilibrium eccentricity is larger. Note that these low frequency modes are essentially disc modes and are associated with low interior protoplanet eccentricities when the latter are present. Such disc modes may also be associated with high embedded protoplanet eccentricities through secular resonances (see Sect. 4 above). In our models such resonances occur when the pattern speed is slightly prograde. An example is shown in Fig. 9. This occurs for the one protoplanet model with disc B at about 20 times the radius of the disc inner edge. Such a resonance also occurs when disc model A is used but for a higher order mode at smaller radii (see Fig. 8).
To give numerical examples we first consider the two protoplanet
model with disc A as an approximation to the
Upsilon Andromedae system. Taking the situation represented in
Fig. 2 with inner boundary disc eccentricity
0.1, for a semi-major axis of 2.57 AU for the outer protoplanet
in the inner cavity, being 0.6 of the inner boundary
radius, r=1.5 corresponds to
6.4 AU. For
the mode with
![]() and disc model A,
and disc model A,
![]() at r = 1.5.At this radius e=0.07, and the equilibrium
eccentricity
at r = 1.5.At this radius e=0.07, and the equilibrium
eccentricity
![]() From Fig. 12 the orbital migration
rate is very small and possibly outwards. We also find
From Fig. 12 the orbital migration
rate is very small and possibly outwards. We also find
![]() yr and
yr and
![]() Thus in this case the eccentric disc
has significant effects on the tidal torques acting on an embedded
protoplanet.
Thus in this case the eccentric disc
has significant effects on the tidal torques acting on an embedded
protoplanet.
The eccentricity of the outermost protoplanet orbit in
the inner cavity
would be ![]() 0.1. The currently observed value which is three or so
times larger would be attained if the disc inner boundary was scaled
to be at twice the outer protoplanet semi-major axis.
Very similar results for the migration and circularization rates
to those obtained above would still apply.
0.1. The currently observed value which is three or so
times larger would be attained if the disc inner boundary was scaled
to be at twice the outer protoplanet semi-major axis.
Very similar results for the migration and circularization rates
to those obtained above would still apply.
As an example to illustrate a case involving a very low frequency mode we consider the one protoplanet model with disc A. The modes are plotted in Fig. 4 and the equilibrium eccentricities in Fig. 8.
For
the mode with
![]() we find that
at r=10
we find that
at r=10
![]() Supposing that r=10 corresponds to 5 AU,
Supposing that r=10 corresponds to 5 AU,
![]() From Fig. 12 we find that for e=0.05, there is
torque reversal.
We also again find that
From Fig. 12 we find that for e=0.05, there is
torque reversal.
We also again find that
![]() yr and
yr and
![]()
These examples indicate that protoplanets embedded in eccentric discs will be in eccentric orbits and that based on resonant torque calculations orbital migration slows down and may even reverse to become outward when the protoplanet eccentricity is sufficiently large. However, we should emphasize that these calculations are approximate and somewhat uncertain due to the cancellation of torques arising at inner and outer Lindblad resonances. To further examine the issue of protoplanet disc tidal interaction at a large eccentricity ( compared to H/r and e) we present below a simpler calculation based on local dynamical friction which should apply in the appropriate limit and which is in essential qualitative agreement with the resonant torque calculations.
Accordingly we work in a reference frame moving instantaneously
with the protoplanet in which the disc material appears
to move with velocity ![]() Adopting local Cartesian
coordinates, we suppose that the perturbing potential due to
the protoplanet may be written as Fourier integral
Adopting local Cartesian
coordinates, we suppose that the perturbing potential due to
the protoplanet may be written as Fourier integral
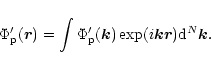 |
(52) |
In each case, assuming a local steady
state, the velocity ![]() induced by the protoplanet
is found from
induced by the protoplanet
is found from
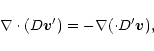 |
(54) |
The rate of change of disc momentum
![]() which gives rise to a frictional force
on the protoplanet acting in the direction
of it's relative velocity,
may then be calculated from
which gives rise to a frictional force
on the protoplanet acting in the direction
of it's relative velocity,
may then be calculated from
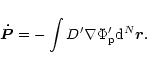 |
(55) |
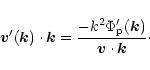 |
(57) |
Using (58) we may evaluate, remembering
that ![]() is the relative velocity between
disc and protoplanet, the average rate of change
of angular momentum of the protoplanet from
is the relative velocity between
disc and protoplanet, the average rate of change
of angular momentum of the protoplanet from
In the two dimensional case for
![]() one obtains for small
one obtains for small ![]() and e =0.
and e =0.
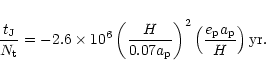 |
(61) |
We may also use the above formalism to calculate
the mean rate of change of orbital energy for the protoplanet
to be
Performing the integration we find
for small ![]() and assuming
and assuming
![]() that
that
We further comment that the more sensitive dependence on the softening parameter means that two dimensional calculations of the type carried out here, require a precise specification of this parameter that correctly represents three dimensional effects in order for them to be very accurate. Thus two dimensional torque calculations and use of torque formulae such as (43) suffer from a number of uncertainties which can be of comparable importance.
Copyright ESO 2002