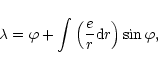 |
(33) |
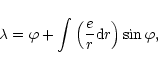 |
(33) |
In a general orthogonal coordinate system in which the disc
appears to be in a steady state, the equations of motion
for the velocity
![]() may then be written (see Appendix 2)
may then be written (see Appendix 2)
When considering the response to an embedded protoplanet, we are interested in responses with a scale
H and azimuthal mode number
![]() Here for the time being
Here for the time being ![]() is regarded as the azimuthal angle.
We perform a response calculation by linearizing
Eqs. (34) and (35) about the steady state
described above.
We may expand the linearized equations in powers of the disc eccentricity.
is regarded as the azimuthal angle.
We perform a response calculation by linearizing
Eqs. (34) and (35) about the steady state
described above.
We may expand the linearized equations in powers of the disc eccentricity.
Here we shall work only to lowest order and neglect terms of order e times smaller than the dominant ones
which, linearizing (34) and (35) directly and
denoting perturbation quantities by a prime, are of order
![]() In this scheme we may replace
In this scheme we may replace
![]() and
and
![]() by unity except where the latter
occurs in the combination
by unity except where the latter
occurs in the combination
![]() with
with
![]() here denoting the unperturbed velocity in the disc.
This is because the contribution of terms of first order in the eccentricity to this operator
leads to
quantities of order
here denoting the unperturbed velocity in the disc.
This is because the contribution of terms of first order in the eccentricity to this operator
leads to
quantities of order
![]() in the linearized equations.
For
in the linearized equations.
For
![]() these are comparable to the dominant terms. All other eccentricity
contributions are smaller by a factor at most
these are comparable to the dominant terms. All other eccentricity
contributions are smaller by a factor at most ![]() .
.
We have to first order in eccentricity
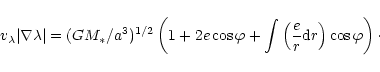 |
(36) |
To lowest order in e, the coordinates (a,M) behave just like the cylindrical coordinates
![]() in the sense that one may make the replacements
in the sense that one may make the replacements
![]() in the standard linearized equations
expressed in cylindrical coordinates.
However, recall that in the forcing potential
in the standard linearized equations
expressed in cylindrical coordinates.
However, recall that in the forcing potential
![]() we must make the replacement (37)
which can be thought of evaluation on an eccentric disc orbit.
we must make the replacement (37)
which can be thought of evaluation on an eccentric disc orbit.
For an eccentric protoplanet orbit with semi-major axis ![]() and eccentricity
and eccentricity
![]() we have
we have
Using (37) and (39), we perform the Fourier
decomposition
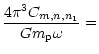 |
|||
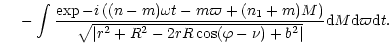 |
(40) |
An important aspect of the linearized problem expressed in terms of the coordinates a,M is that the separable coordinates are t and M.Accordingly a separable response occurs to a combination of terms in the Fourier decomposition with fixed (n1+m) =k1 and (n-m)=k2.
Thus for such a particular forcing term with fixed (k1,k2)
A novel feature is that, unlike in the case of a forced axisymmetric disc,
a separated forcing
potential component in general depends on ![]() This is because the angle between the apsidal lines of
the disc and protoplanet orbits
can have physical significance. But note that when both protoplanet
and disc eccentricity are zero only one term can survive
in (42) when
m = k1 = - k2 and then
This is because the angle between the apsidal lines of
the disc and protoplanet orbits
can have physical significance. But note that when both protoplanet
and disc eccentricity are zero only one term can survive
in (42) when
m = k1 = - k2 and then ![]() appears
only as a redundant complex phase.
appears
only as a redundant complex phase.
For the general forcing term (41) the pattern speed
![]() We shall consider the situation when
the disc surface density
We shall consider the situation when
the disc surface density
![]() as is the
case in our models away from the boundaries. Then corotation
resonances may be ignored and the main interaction
is through wave excitation at the Lindblad resonances
(e.g. Goldreich & Tremaine 1978). These occur when
as is the
case in our models away from the boundaries. Then corotation
resonances may be ignored and the main interaction
is through wave excitation at the Lindblad resonances
(e.g. Goldreich & Tremaine 1978). These occur when
![]() with
with
![]() (e.g. Artymowicz 1993).
For k1 >0, the positive sign applies to the outer Lindblad resonance (OLR)
and the negative sign to the inner Lindblad resonance (ILR).
In both cases a wave is excited that propagates away from the protoplanet.
The waves are associated with an outward energy and angular momentum flux.
In the case of the ILR, the background rotates faster than the wave
so that as it dissipates, energy and angular momentum
are transferred to the protoplanet orbit.
In the case of the OLR, the background rotates more slowly
so that energy and angular momentum are removed from the protoplanet orbit.
(e.g. Artymowicz 1993).
For k1 >0, the positive sign applies to the outer Lindblad resonance (OLR)
and the negative sign to the inner Lindblad resonance (ILR).
In both cases a wave is excited that propagates away from the protoplanet.
The waves are associated with an outward energy and angular momentum flux.
In the case of the ILR, the background rotates faster than the wave
so that as it dissipates, energy and angular momentum
are transferred to the protoplanet orbit.
In the case of the OLR, the background rotates more slowly
so that energy and angular momentum are removed from the protoplanet orbit.
Because the linearized response
problem is formally identical to the one obtained for
an axisymmetric disc
![]() ,
consistent with he other approximations
we have made, we can evaluate the outward energy flow rate associated
with outward propagating waves
using the approximate
expressions developed by Artymowicz (1993) and Ward (1997) which
depend only on the disc state variables evaluated at the
respective resonances. We comment that there are uncertainties
associated with the use of these expressions in evaluating orbital
evolution rates especially when they are derived by summing
torque contributions with varying signs. However, cancellation
effects do not appear to be significant
(Artymowicz 1993; Ward 1997) and as they are supported by general
considerations, we believe that the main features of the results
derived to be correct. Following this procedure,
the outward energy flow rate associated
with outward propagating waves is given by
,
consistent with he other approximations
we have made, we can evaluate the outward energy flow rate associated
with outward propagating waves
using the approximate
expressions developed by Artymowicz (1993) and Ward (1997) which
depend only on the disc state variables evaluated at the
respective resonances. We comment that there are uncertainties
associated with the use of these expressions in evaluating orbital
evolution rates especially when they are derived by summing
torque contributions with varying signs. However, cancellation
effects do not appear to be significant
(Artymowicz 1993; Ward 1997) and as they are supported by general
considerations, we believe that the main features of the results
derived to be correct. Following this procedure,
the outward energy flow rate associated
with outward propagating waves is given by
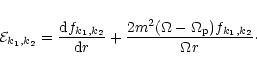
One can find the outward angular momentum flow rate produced directly
by the protoplanet
associated with the linear response
using
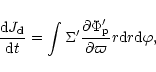 |
(44) |
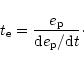 |
(48) |
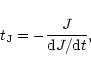 |
(49) |
Copyright ESO 2002