

Up: Global modes and migration
Subsections
4 The motion of a low mass
protoplanet in an eccentric disc
The evolution of the coplanar orbit of an interior protoplanet
in the earth mass range embedded in the disc
due to the gravitational interaction
with the slowly precessing disc can be found using secular perturbation theory.
We regard the embedded protoplanet as a test particle
evolving in a prescribed
gravitational potential and neglect the influence of the protoplanet on the
disc mode. This should be reasonable when as here, the angular momentum
of the protoplanet is significantly less than that of the material supporting
the normal mode (e.g. Papaloizou et al. 2001).
The orbit evolves under the perturbing potential per unit mass,
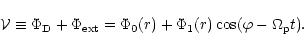 |
(23) |
Here 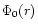 is the axisymmetric component of the potential
but excluding that due to the central mass and
is the axisymmetric component of the potential
but excluding that due to the central mass and 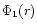 is the radial
amplitude of the m=1 component arising from the normal mode.
is the radial
amplitude of the m=1 component arising from the normal mode.
On performing a time average over the protoplanet orbit
one obtains the Hamiltonian system:
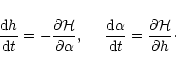 |
(24) |
Here
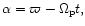 with
with 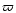 being the longtitude of
periapse and
being the longtitude of
periapse and
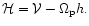 The specific angular momentum is
The specific angular momentum is
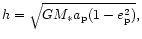
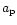 is the constant semi-major axis,
and
is the constant semi-major axis,
and 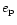 is the eccentricity.
To leading powers of
is the eccentricity.
To leading powers of 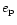 we have
we have
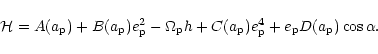 |
(25) |
Hamilton's equations then give to leading powers of 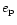
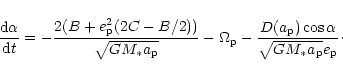 |
(26) |
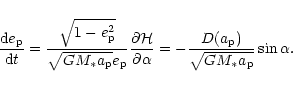 |
(27) |
Here the precession rate of the apsidal line induced by
the axisymmetric potential, to first order in
the perturbing potential, expressed as an expansion in powers
of 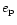 is given by the first term on the right hand
of Eq. (26) as
is given by the first term on the right hand
of Eq. (26) as
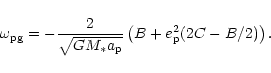 |
(28) |
This may also be written in terms of the axisymmetric
component of the potential directly as
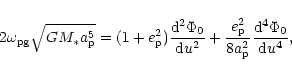 |
(29) |
where u=1/r, and r is taken to be equal to
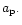
Equilibrium or steady state solutions of (26)
and (27) with 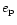 and
and 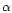 constant
occur when
constant
occur when 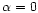 or
or
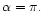 Adopting the convention that
Adopting the convention that 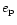 is positive suffices
to select one of the latter possibilities as
(26) gives an expression from which
is positive suffices
to select one of the latter possibilities as
(26) gives an expression from which 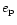 can be determined in the form
can be determined in the form
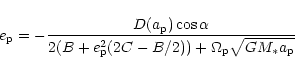 |
(30) |
or equivalently
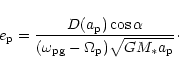 |
(31) |
Alternatively one may fix 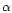 to be 0 or
to be 0 or 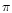 and allow
and allow 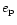 to change sign as we have done for the normal modes.
to change sign as we have done for the normal modes.
An equilibrium solution so determined corresponds to the situation
when the protoplanet orbit precesses at the same rate,
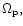 as the mass distribution
that produces the gravitational potential while maintaining a constant
eccentricity. Assuming that
as the mass distribution
that produces the gravitational potential while maintaining a constant
eccentricity. Assuming that
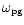 and
and
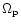 are of comparable magnitude, in general
for modest eccentricity,
are of comparable magnitude, in general
for modest eccentricity,
and is proportional to the magnitude of the nonaxisymmetric potential.
An exception occurs when
In this case, the precession frequency
of a free orbit with small eccentricity,
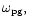 matches that
of the nonaxisymmetric mass distribution
matches that
of the nonaxisymmetric mass distribution
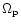 corresponding to a secular resonance.
When this occurs Eq. (30) indicates that
corresponding to a secular resonance.
When this occurs Eq. (30) indicates that
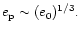 Accordingly significantly larger equilibrium eccentricities are expected
close to a secular resonance. We comment that for fixed
Accordingly significantly larger equilibrium eccentricities are expected
close to a secular resonance. We comment that for fixed 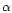
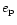 changes sign as a secular resonance is passed through corresponding
to an alignment change through a rotation of the axis of the ellipse through
changes sign as a secular resonance is passed through corresponding
to an alignment change through a rotation of the axis of the ellipse through 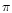 .
.
One may also investigate the effect of orbital circularization
by adding a term
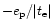 to the right hand side
of (27), where
to the right hand side
of (27), where
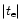 is the circularization time.
In this case one can still find an equilibrium but with orbital
apsidal line rotated. Restricting consideration to the situation
away from secular resonance, one finds that the equilibrium eccentricity
is reduced by a factor
is the circularization time.
In this case one can still find an equilibrium but with orbital
apsidal line rotated. Restricting consideration to the situation
away from secular resonance, one finds that the equilibrium eccentricity
is reduced by a factor
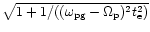 and
and
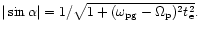 Thus when
Thus when
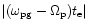 is large,
the effect of the circularization term is to produce
a small rotation of the apsidal line of the orbit.
is large,
the effect of the circularization term is to produce
a small rotation of the apsidal line of the orbit.
As indicated above equilibrium solutions correspond to the situation where
the apsidal precession
of the protoplanet orbit is locked to that of the underlying nonaxisymmetric disc.
One can find solutions undergoing small librations in the neighbourhood
of equilibrium
solutions (e.g. Brouwer & Clemence 1961) and when dissipative forces
are added
these may decay making the attainment of equilibrium solutions natural.
As we indicate below, tidal interaction of a protoplanet with the disc may
produce such dissipative forces. Accordingly we shall focus
on equilibrium solutions in what follows below.
It is a simple matter to determine equilibrium
eccentricities for protoplanets moving under the gravitational
potential appropriate to a normal mode corresponding
to an eccentric disc, with pattern speed
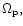 of the type calculated above.
We recall the normal mode Eq. (18)
which can be regarded as determining the equilibrium
disc eccentricity in the form
of the type calculated above.
We recall the normal mode Eq. (18)
which can be regarded as determining the equilibrium
disc eccentricity in the form
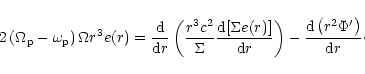 |
(32) |
If the pressure forces are neglected by dropping
the terms involving c2, this is exactly equivalent
to Eq. (31) for determining the
protoplanet eccentricity with e(r) corresponding
to 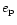 and
and
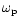 replaced by
replaced by
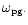 Thus a local protoplanet equilibrium eccentricity
appropriate to a disc mode or response
can be determined by using the disc normal mode Eq. (18)
retaining the term resulting from the disc self-gravity but omitting
pressure contributions.
Thus a local protoplanet equilibrium eccentricity
appropriate to a disc mode or response
can be determined by using the disc normal mode Eq. (18)
retaining the term resulting from the disc self-gravity but omitting
pressure contributions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig8.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg129.gif) |
Figure 8:
This figure shows the form of the
equilibrium eccentricity
as a function of radius r in units of
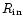 for the modes shown in Fig. 4,
the latter being normalized so that e=0.1 for r=1.Curves are associated with normal modes according to
increasing number of nodes. Thus the curve with the most
nodes is associated with the normal mode
with the most nodes. Note the secular resonances for r <5. for the modes shown in Fig. 4,
the latter being normalized so that e=0.1 for r=1.Curves are associated with normal modes according to
increasing number of nodes. Thus the curve with the most
nodes is associated with the normal mode
with the most nodes. Note the secular resonances for r <5. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig9.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg130.gif) |
Figure 9:
As in Fig. 8 but for the
one planet model with disc model B.
Equilibrium curves are given for the two highest frequency
modes only. That associated with the highest frequency
decays to small values at about r=5.The other curve shows a strong secular resonance
at
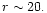 |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig10.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg131.gif) |
Figure 10:
As in Fig. 8 but for the disc model A
with no protoplanets. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig11.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg132.gif) |
Figure 11:
As in Fig. 10 but for the disc model B
with no protoplanets. In this case the longest wavelength equilibrium
eccentricity indicates antialignment with the disc. |
This procedure should be applicable provided
the eccentricities are not too large. Equilibrium eccentricities
are plotted for some of the normal modes we calculated
in Figs. 2 and 3 and also 8-11.
In Figs. 2 and 3 we also plot equilibrium eccentricities
but calculated with the nonaxisymmetric contribution to the gravitational
potential due to the disc removed which is equivalent to
assuming that it remains circular. We see that the assumption that
disc remains circular results in a
significantly smaller equilibrium eccentricity for disc model A,
particularly for the mode with second highest frequency.
For the lower mass disc model B, differences arising
fom assuming the disc
remains circular are less pronounced.
We also coment that the occurence of secular resonances
in the inner parts of the disc where
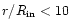 is common.
is common.
One expects that dissipative torques produced by protoplanet-disc tidal
interaction may result in the approach to such equilibrium
solutions from general initial conditions. This we now discuss.


Up: Global modes and migration
Copyright ESO 2002
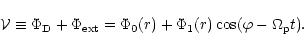
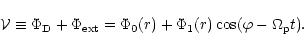
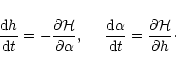
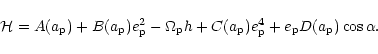
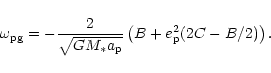
![]() and
and ![]() constant
occur when
constant
occur when ![]() or
or
![]() Adopting the convention that
Adopting the convention that ![]() is positive suffices
to select one of the latter possibilities as
(26) gives an expression from which
is positive suffices
to select one of the latter possibilities as
(26) gives an expression from which ![]() can be determined in the form
can be determined in the form
![]() as the mass distribution
that produces the gravitational potential while maintaining a constant
eccentricity. Assuming that
as the mass distribution
that produces the gravitational potential while maintaining a constant
eccentricity. Assuming that
![]() and
and
![]() are of comparable magnitude, in general
for modest eccentricity,
are of comparable magnitude, in general
for modest eccentricity,
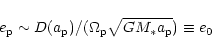
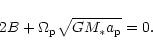
![]() to the right hand side
of (27), where
to the right hand side
of (27), where
![]() is the circularization time.
In this case one can still find an equilibrium but with orbital
apsidal line rotated. Restricting consideration to the situation
away from secular resonance, one finds that the equilibrium eccentricity
is reduced by a factor
is the circularization time.
In this case one can still find an equilibrium but with orbital
apsidal line rotated. Restricting consideration to the situation
away from secular resonance, one finds that the equilibrium eccentricity
is reduced by a factor
![]() and
and
![]() Thus when
Thus when
![]() is large,
the effect of the circularization term is to produce
a small rotation of the apsidal line of the orbit.
is large,
the effect of the circularization term is to produce
a small rotation of the apsidal line of the orbit.
![]() of the type calculated above.
We recall the normal mode Eq. (18)
which can be regarded as determining the equilibrium
disc eccentricity in the form
of the type calculated above.
We recall the normal mode Eq. (18)
which can be regarded as determining the equilibrium
disc eccentricity in the form
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig8.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg129.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig9.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg130.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig10.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg131.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig11.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg132.gif)