Up: Global modes and migration
3 Normal modes
We have calculated the lowest order global normal modes
for two different configurations involving protoplanets
orbiting interior to the disc in an inner cavity.
The first, approximating the Upsilon Andromedae
system involves two protoplanets with mass ratios 0.00383and 0.00196 orbiting at
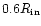 and
and
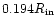 respectively. However, the disc normal modes do not change much
in character if the protoplanet orbital radii are scaled
to somewhat smaller fractions of
respectively. However, the disc normal modes do not change much
in character if the protoplanet orbital radii are scaled
to somewhat smaller fractions of
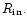 But the ratio of protoplanet
to disc eccentricity in the joint modes changes more significantly.
The second configuration we consider is
a single protoplanet with mass ratio 0.002 orbiting at
But the ratio of protoplanet
to disc eccentricity in the joint modes changes more significantly.
The second configuration we consider is
a single protoplanet with mass ratio 0.002 orbiting at
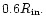 Finally we consider a disc with no interior orbiting protoplanets.
In all of these cases
we consider both model A and model B discs.
Finally we consider a disc with no interior orbiting protoplanets.
In all of these cases
we consider both model A and model B discs.
The pattern speeds for the highest frequency normal modes
and the protoplanet orbital
eccentricities occurring jointly with the normal modes
are given in Table 1.
For the results presented here,
the modes are normalized such that the disc eccentricity at the inner
boundary is 0.1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.ps}\end{figure}](/articles/aa/full/2002/23/aa2149/Timg82.gif) |
Figure 2:
This figure shows the first two modes
and the associated equilibrium eccentricities
as a function of radius r in units of
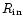 for the two protoplanet case with disc model A.
The two modes (full curves)
are normalized so that e=0.1 at r=1. The lower curve
corresponds to the mode of highest frequency given in Table 1.
The dotted curves give the associated equilibrium eccentricities
calculated for a low mass
protoplanet orbiting within the disc,
the lowermost corresponding to the highest frequency mode.
The dashed curve gives the equilibrium eccentricity for a low mass
protoplanet orbiting within the disc calculated for the
highest frequency mode but neglecting the non axisymmetric component
of the disc potential. The dot dashed curve
gives the corresponding plot for the other mode.
The latter curves indicate the presence
of secular resonances at for the two protoplanet case with disc model A.
The two modes (full curves)
are normalized so that e=0.1 at r=1. The lower curve
corresponds to the mode of highest frequency given in Table 1.
The dotted curves give the associated equilibrium eccentricities
calculated for a low mass
protoplanet orbiting within the disc,
the lowermost corresponding to the highest frequency mode.
The dashed curve gives the equilibrium eccentricity for a low mass
protoplanet orbiting within the disc calculated for the
highest frequency mode but neglecting the non axisymmetric component
of the disc potential. The dot dashed curve
gives the corresponding plot for the other mode.
The latter curves indicate the presence
of secular resonances at
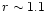 associated with both modes.
associated with both modes. |
Many of the properties of these modes can be
understood with reference to the local
dispersion relation for density waves in the low frequency limit
(Lin & Shu 1969) in the form
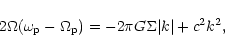 |
(22) |
where k is the radial wavenumber.
The above indicates that when self-gravity, governed
by the first term on the right hand side, is unimportant
as occurs for either low mass discs or large |k|,
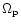 is negative.
On the other hand positive
is negative.
On the other hand positive
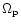 can occur for low |k|or massive discs. Thus in that case the lowest order modes (in terms of numbers of nodes)
should be prograde with more of these existing for more
massive discs, a trend we find in our results.
There can also be very low frequency (in magnitude) modes for which
the self-gravity and pressure terms approximately cancel.
This occurs when
can occur for low |k|or massive discs. Thus in that case the lowest order modes (in terms of numbers of nodes)
should be prograde with more of these existing for more
massive discs, a trend we find in our results.
There can also be very low frequency (in magnitude) modes for which
the self-gravity and pressure terms approximately cancel.
This occurs when
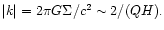 For
For
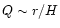 as in the models here, this is comparable
to the radius making a very global mode.
as in the models here, this is comparable
to the radius making a very global mode.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig3.ps}\end{figure}](/articles/aa/full/2002/23/aa2149/Timg85.gif) |
Figure 3:
As in Fig. 2 but for disc model B.
In this case there is a secular resonance asociated with the
highest frequency mode at
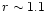 .
For the other mode
this occurs at .
For the other mode
this occurs at
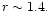 |
As we calculate normal modes jointly involving protoplanets and disc,
the protoplanets have associated eccentricities.
In general the 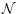 highest frequency modes predominantly
involve the protoplanets while the others predominantly
involve the disc,
highest frequency modes predominantly
involve the protoplanets while the others predominantly
involve the disc, 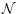 being the number of protoplanets.
The two highest frequency modes for the two protoplanet
case are plotted in Fig. 2 for disc model A
and in Fig. 3 for disc model B.
For the second highest frequency mode calculated for
disc model A, the protoplanet
eccentricity ratio is 1.38, while for model B it is 1.88.
The latter result is similar to that given by
Chiang et al. (2001) who considered the
current Upsilon Andromedae system with no disc and
concluded it was predominantly in this mode.
being the number of protoplanets.
The two highest frequency modes for the two protoplanet
case are plotted in Fig. 2 for disc model A
and in Fig. 3 for disc model B.
For the second highest frequency mode calculated for
disc model A, the protoplanet
eccentricity ratio is 1.38, while for model B it is 1.88.
The latter result is similar to that given by
Chiang et al. (2001) who considered the
current Upsilon Andromedae system with no disc and
concluded it was predominantly in this mode.
The results found here suggest the disc and protoplanet
orbits were antialigned. With the outermost protoplanet
at
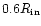 the disc inner boundary
and outer protoplanet eccentricities are comparable
for model A while for model B the relative disc eccentricity
is 56 percent smaller.
However, when the outer protoplanet orbits at
the disc inner boundary
and outer protoplanet eccentricities are comparable
for model A while for model B the relative disc eccentricity
is 56 percent smaller.
However, when the outer protoplanet orbits at
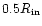 the disc inner boundary
eccentricity is only 1/3 that
of the protoplanet for model A and 19 percent for model B.
Apart from the eccentricity scaling relative to the
interior protoplanets, the spatial form
of the eigenfunction in the disc remains almost identical.
the disc inner boundary
eccentricity is only 1/3 that
of the protoplanet for model A and 19 percent for model B.
Apart from the eccentricity scaling relative to the
interior protoplanets, the spatial form
of the eigenfunction in the disc remains almost identical.
The four highest frequency modes for the one protoplanet
case with disc model A are plotted in Figs. 4 and 5 for model B.
Pure disc modes
with no protoplanet are plotted in Fig. 6 for model A
and Fig. 7 for model B. The modes develop increasing
numbers of nodes as their frequency decreases but the mode
with lowest frequency in absolute magnitude can be very global
with only a few nodes out to
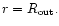 We comment that the modes are rather non compressive
requiring eccentricities of order unity to provide Lagrangian
changes in surface density of order unity. As the motion in the modes
in linear theory
is assumed epicyclic, this is suggestive that the analysis should be valid
as long as the epicyclic approximation is.
We comment that the modes are rather non compressive
requiring eccentricities of order unity to provide Lagrangian
changes in surface density of order unity. As the motion in the modes
in linear theory
is assumed epicyclic, this is suggestive that the analysis should be valid
as long as the epicyclic approximation is.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig4.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg89.gif) |
Figure 4:
This figure shows the four highest frequency
modes
as a function of radius r in units of
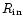 for the one planet model with disc A. The eccentricities
are all normalized so that e = 0.1 at r=1.The modes can be identified by noting that the number of nodes
increases with decreasing eigenfrequency. for the one planet model with disc A. The eccentricities
are all normalized so that e = 0.1 at r=1.The modes can be identified by noting that the number of nodes
increases with decreasing eigenfrequency. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig5.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg90.gif) |
Figure 5:
As in Fig. 4 but for the one planet
model with disc model B. |
Apart fom the two modes with highest
frequency, other normal modes are essentially pure disc modes with only
small associated protoplanet eccentricities.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig6.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg91.gif) |
Figure 6:
As in Fig. 4 but
for the disc model A with no protoplanets. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig7.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg92.gif) |
Figure 7:
As in Fig. 6 but
with disc model B. |
Having calculated these modes that may be largely driven by protoplanets
in eccentric orbits or possibly self-excited or long lived structures
we now go on to consider the migration of low mass protoplanets
embedded in such eccentric discs.
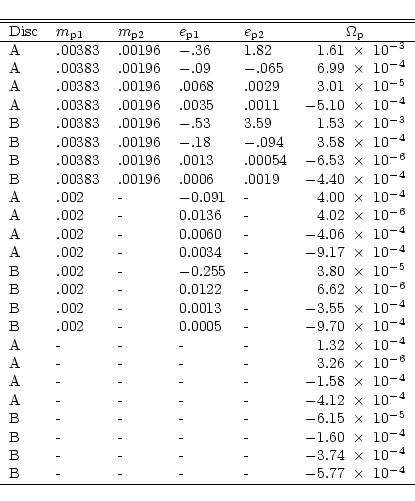
Table 1:
This table gives the protoplanet orbital
eccentricities where appropriate together
with the pattern speeds for the normal modes
calculated. The disc model used is indicated in the first column,
the protoplanet mass ratios to the central star
in the second and third columns, their
orbital eccentricities in the fourth and fifth column and
the mode frequency or pattern speed in the sixth column.
The modes are normalized such that the disc eccentricity at the inner
boundary is 0.1. A negative protoplanet eccentricity then indicates
the orbit is antialigned with the disc.
|
|


Up: Global modes and migration
Copyright ESO 2002
![]() and
and
![]() respectively. However, the disc normal modes do not change much
in character if the protoplanet orbital radii are scaled
to somewhat smaller fractions of
respectively. However, the disc normal modes do not change much
in character if the protoplanet orbital radii are scaled
to somewhat smaller fractions of
![]() But the ratio of protoplanet
to disc eccentricity in the joint modes changes more significantly.
The second configuration we consider is
a single protoplanet with mass ratio 0.002 orbiting at
But the ratio of protoplanet
to disc eccentricity in the joint modes changes more significantly.
The second configuration we consider is
a single protoplanet with mass ratio 0.002 orbiting at
![]() Finally we consider a disc with no interior orbiting protoplanets.
In all of these cases
we consider both model A and model B discs.
Finally we consider a disc with no interior orbiting protoplanets.
In all of these cases
we consider both model A and model B discs.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.ps}\end{figure}](/articles/aa/full/2002/23/aa2149/Timg82.gif)
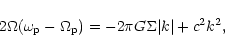
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig3.ps}\end{figure}](/articles/aa/full/2002/23/aa2149/Timg85.gif)
![]() the disc inner boundary
and outer protoplanet eccentricities are comparable
for model A while for model B the relative disc eccentricity
is 56 percent smaller.
However, when the outer protoplanet orbits at
the disc inner boundary
and outer protoplanet eccentricities are comparable
for model A while for model B the relative disc eccentricity
is 56 percent smaller.
However, when the outer protoplanet orbits at
![]() the disc inner boundary
eccentricity is only 1/3 that
of the protoplanet for model A and 19 percent for model B.
Apart from the eccentricity scaling relative to the
interior protoplanets, the spatial form
of the eigenfunction in the disc remains almost identical.
the disc inner boundary
eccentricity is only 1/3 that
of the protoplanet for model A and 19 percent for model B.
Apart from the eccentricity scaling relative to the
interior protoplanets, the spatial form
of the eigenfunction in the disc remains almost identical.
![]() We comment that the modes are rather non compressive
requiring eccentricities of order unity to provide Lagrangian
changes in surface density of order unity. As the motion in the modes
in linear theory
is assumed epicyclic, this is suggestive that the analysis should be valid
as long as the epicyclic approximation is.
We comment that the modes are rather non compressive
requiring eccentricities of order unity to provide Lagrangian
changes in surface density of order unity. As the motion in the modes
in linear theory
is assumed epicyclic, this is suggestive that the analysis should be valid
as long as the epicyclic approximation is.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig5.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig6.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg91.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig7.ps}
\end{figure}](/articles/aa/full/2002/23/aa2149/Timg92.gif)