

Up: Global modes and migration
Subsections
2 Basic equations and their linearized form
for large scale global modes with
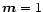
We work in a non rotating cylindrical coordinate system
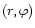 which may initially be considered to be centred on the primary star.
The basic equations of motion in a two dimensional approximation
which should be appropriate for a large scale description
of the disc are taken to be
which may initially be considered to be centred on the primary star.
The basic equations of motion in a two dimensional approximation
which should be appropriate for a large scale description
of the disc are taken to be
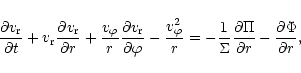 |
(1) |
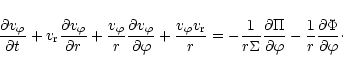 |
(2) |
In addition we have the two dimensional form of the continuity equation
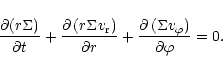 |
(3) |
Here the velocity is
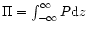 represents a vertically integrated pressure
which we assume to be a function of the surface density
represents a vertically integrated pressure
which we assume to be a function of the surface density 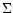 defined by
defined by
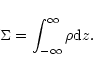 |
(4) |
The sound speed is then given by
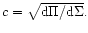 The gravitational
potential
The gravitational
potential
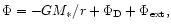 with G being the gravitational constant,
has a point mass contribution arising from
the
central mass
M*, a contribution,
with G being the gravitational constant,
has a point mass contribution arising from
the
central mass
M*, a contribution,
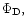 due to the disc
and a contribution,
due to the disc
and a contribution,
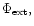 due to external protoplanets.
due to external protoplanets.
The unperturbed disk is axisymmetric
with no radial motion such that
the velocity
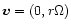 with
with
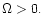 In equilibrium we then have from Eq. (1)
In equilibrium we then have from Eq. (1)
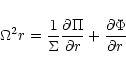 |
(5) |
and the gravitational
potential
due to the disc is given by
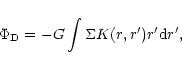 |
(6) |
with
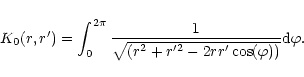 |
(7) |
We allow for the effects of orbiting external protoplanets
which provide
the external potential
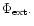 In this paper we are primarily interested
in phenomena which vary on a time scale
long compared to a local orbital period.
Accordingly we use the time averaged or secular
protoplanet perturbing potential which is
derived in Appendix 1. For a single protoplanet
of mass
In this paper we are primarily interested
in phenomena which vary on a time scale
long compared to a local orbital period.
Accordingly we use the time averaged or secular
protoplanet perturbing potential which is
derived in Appendix 1. For a single protoplanet
of mass 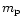 and orbital radius
and orbital radius
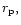 the contribution
to the external potential is given by
the contribution
to the external potential is given by
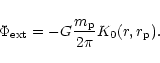 |
(8) |
In a thin disc of the kind considered here, the contributions
due to pressure and self-gravity are comparable and small leading to
nearly Keplerian rotation which has
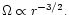 When
When
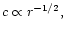 the disc then has a nearly constant putative
aspect ratio
the disc then has a nearly constant putative
aspect ratio
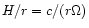 ,
H being the putative semi thickness.
Here we are interested in global m=1 modes
with slowly varying pattern when viewed in the adopted reference frame.
To study these, we linearize the basic equations
about the equilibrium state
denoting perturbations to
quantities with a prime.
As usual we assume that the dependence of all perturbations
(in cylindrical coordinates) on
,
H being the putative semi thickness.
Here we are interested in global m=1 modes
with slowly varying pattern when viewed in the adopted reference frame.
To study these, we linearize the basic equations
about the equilibrium state
denoting perturbations to
quantities with a prime.
As usual we assume that the dependence of all perturbations
(in cylindrical coordinates) on 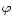 and tis through a factor
and tis through a factor
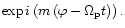 For the slowly varying modes we consider
For the slowly varying modes we consider
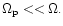 The linearized forms of Eqs. (1)-(3) are
then
The linearized forms of Eqs. (1)-(3) are
then
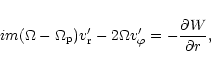 |
(9) |
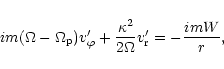 |
(10) |
and
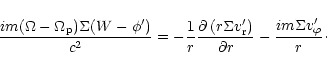 |
(11) |
Here
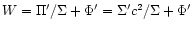 ,
and
,
and
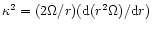 denotes the square of the epicyclic frequency.
denotes the square of the epicyclic frequency.
For the gravitational potential perturbation we have
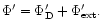 Here we shall allow
for the contribution
of the secular effects of other sources
such as protoplanets to the modes through the
gravitational potential perturbation
Here we shall allow
for the contribution
of the secular effects of other sources
such as protoplanets to the modes through the
gravitational potential perturbation
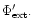
We consider linear perturbations of an
axisymmetric disc that correspond to normal modes with m=1that make it eccentric. The modes we consider are
such that
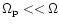 and the dominant
motion is epicyclic. In this case, to lowest order,
we may neglect the pressure and self-gravity term Was well as
and the dominant
motion is epicyclic. In this case, to lowest order,
we may neglect the pressure and self-gravity term Was well as
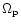 and assume
and assume 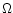 is keplerian, to obtain from Eq. (10)
is keplerian, to obtain from Eq. (10)
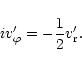 |
(12) |
Using the above and introducing the radial Lagrangian displacement
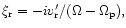 Eq. (11) gives
the
surface density perturbation in the low frequency
limit in the form
Eq. (11) gives
the
surface density perturbation in the low frequency
limit in the form
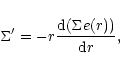 |
(13) |
with
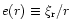 being the disc eccentricity.
being the disc eccentricity.
The gravitational potential perturbation induced by the disc is
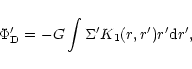 |
(14) |
with
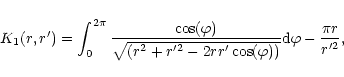 |
(15) |
where the second term corresponds to the indirect term
which results from the acceleration of the coordinate system
produced by the disc material.
The existence of a mode with m=1 in the disc causes
the orbits of the protoplanets
interior to the disc to become eccentric.
Noting the different form of indirect term used,
the secular perturbing potential
derived in Appendix 1 then gives
the contribution of an orbiting protoplanet
to the external potential perturbation to be
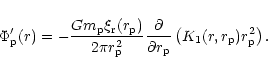 |
(16) |
Here the eccentricity of the
companion orbit is related to the displacement by
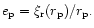 The total external potential perturbation is then found by summing over the
perturbing protoplanets:
The total external potential perturbation is then found by summing over the
perturbing protoplanets:
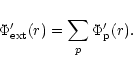 |
(17) |
Eliminating
 from Eqs. (9) and (10),
using Eq. (13) for
from Eqs. (9) and (10),
using Eq. (13) for 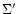 and expanding to first order
in the small frequencies
and expanding to first order
in the small frequencies
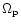 and
and
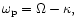 the fluid element orbital precession frequency in the absence
of surface density or gravitational potential
perturbations,
one obtains a
normal mode equation relating
the fluid element orbital precession frequency in the absence
of surface density or gravitational potential
perturbations,
one obtains a
normal mode equation relating
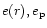 and
and
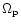 in the form (see also Papaloizou et al. 2001)
in the form (see also Papaloizou et al. 2001)
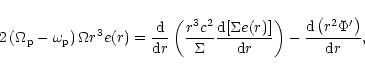 |
(18) |
where, c, is the local sound speed.
In addition we have an equation for each protoplanet
of the form
![\begin{displaymath}2\left(\Omega_{\rm p} - \omega_{\rm p} \right) \Omega(r_{\rm ...
...\left( r^2\Phi'\right) \over {\rm d} r}\right]_{r=r_{\rm p}}
,
\end{displaymath}](/articles/aa/full/2002/23/aa2149/img65.gif) |
(19) |
where of course
for a particular protoplanet there is no self-interaction
term in the sum for
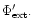 The inclusion of self-gravity in the eigenvalue problem
is essential if modes with prograde precession frequency
are to be obtained.
For typical protoplanetary disc models, self-gravity
can be strong enough to induce prograde precession
for the long wavelength m=1 modes considered here.
The inclusion of self-gravity in the eigenvalue problem
is essential if modes with prograde precession frequency
are to be obtained.
For typical protoplanetary disc models, self-gravity
can be strong enough to induce prograde precession
for the long wavelength m=1 modes considered here.
Normal modes were calculated by discretizing (18) and (19)
and formulating a matrix eigenvalue problem on an unequally
spaced grid with 200 grid points with intervals
increasing in geometric progression (see Terquem & Papaloizou 2000
for consideration of a related problem).
We present here results obtained for a disc model
with equation of state given by a polytrope of index n=1.5.The sound speed is given by
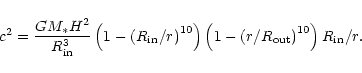 |
(20) |
Here the first two factors provide sharp
edges at the disc inner and outer boundaries and
H/r= 0.05 is the disc aspect ratio away from these boundaries.
The surface density is given by
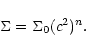 |
(21) |
The boundary regions are chosen to be
of order the disc scale height in width
and away from these
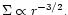 In the above
In the above
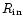 is the inner boundary radius which is taken to
be the unit of length. The unit of mass is the central mass M*and the unit of time is
is the inner boundary radius which is taken to
be the unit of length. The unit of mass is the central mass M*and the unit of time is
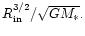 The arbitrary scaling factor
The arbitrary scaling factor 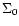 was chosen
such that in model A the total disc mass was
was chosen
such that in model A the total disc mass was
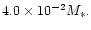 In model B the total disc mass
was
In model B the total disc mass
was
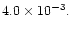
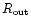 is the outer boundary radius, here,
in order to study large scale modes, taken as
is the outer boundary radius, here,
in order to study large scale modes, taken as
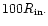
The importance of self gravity is measured by the
Toomre parameter
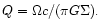 For model A this has a minimum value of 5.2 while for
the lower mass disc model of model B this minimum value
is 52. Another quantity of interest is the local precession frequency
of a test particle orbit
For model A this has a minimum value of 5.2 while for
the lower mass disc model of model B this minimum value
is 52. Another quantity of interest is the local precession frequency
of a test particle orbit
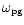 in the axisymmetric
component of the total gravitational
potential (see Eq. (29) below).
in the axisymmetric
component of the total gravitational
potential (see Eq. (29) below).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig1.ps}\end{figure}](/articles/aa/full/2002/23/aa2149/Timg77.gif) |
Figure 1:
This figure shows the local test
particle orbital precession frequency in dimensionless units
as a function of radius, r in units of
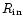 in the range
1.1 <r< 100for the two disc models A (lower curve) and B
with no interior orbiting protoplanets. Apart from small regions
near to the boundaries, the frequency is negative
corresponding to retrograde precession. in the range
1.1 <r< 100for the two disc models A (lower curve) and B
with no interior orbiting protoplanets. Apart from small regions
near to the boundaries, the frequency is negative
corresponding to retrograde precession. |
This is plotted for the two disc models in Fig. 1.
It is small and negative
in dimensionless units over much of the discs,
corresponding to retrograde precession,
scaling with the disc mass as it is determined by the disc self-gravity.
As we shall see this behaviour provides scope for secular
resonance associated with low frequency modes.


Up: Global modes and migration
Copyright ESO 2002
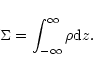
![]() with
with
![]() In equilibrium we then have from Eq. (1)
In equilibrium we then have from Eq. (1)
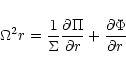
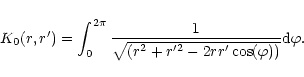
![]() Here we shall allow
for the contribution
of the secular effects of other sources
such as protoplanets to the modes through the
gravitational potential perturbation
Here we shall allow
for the contribution
of the secular effects of other sources
such as protoplanets to the modes through the
gravitational potential perturbation
![]()
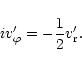
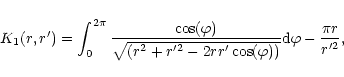
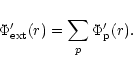
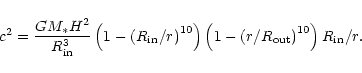
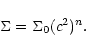
![]() For model A this has a minimum value of 5.2 while for
the lower mass disc model of model B this minimum value
is 52. Another quantity of interest is the local precession frequency
of a test particle orbit
For model A this has a minimum value of 5.2 while for
the lower mass disc model of model B this minimum value
is 52. Another quantity of interest is the local precession frequency
of a test particle orbit
![]() in the axisymmetric
component of the total gravitational
potential (see Eq. (29) below).
in the axisymmetric
component of the total gravitational
potential (see Eq. (29) below).