In order to study the effect proposed by VC2001 in isolation we need to suppress artificially the ordinary dynamo effect due to kinetic helicity of the flow. Following VC2001 the crucial factor that is necessary for causing the anticipated correlation is shear, but not rotation. To check this we have used a simulation of externally driven turbulence with zero net helicity. This is done by using the forcing function of B2001, but with helicity whose sign changes randomly. In addition, the model is supplemented by the effects of sinusoidal shear (as in BBS2001) and vertical stratification with a conducting halo above a turbulent layer (as in BD2001).
We solve the isothermal compressible MHD equations for the logarithmic
density ![]() ,
the velocity
,
the velocity
![]() ,
and the magnetic vector potential
,
and the magnetic vector potential
![]() ,
,
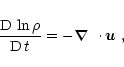 |
(6) |
| (9) |
We use nondimensional units where
![]() .
Here,
.
Here,
![]() is the isothermal sound speed, k1 the smallest wavenumber
of the two horizontal directions (so its size is
is the isothermal sound speed, k1 the smallest wavenumber
of the two horizontal directions (so its size is ![]() in the horizontal
direction). The vertical extent of the domain is
in the horizontal
direction). The vertical extent of the domain is ![]() .
Periodic boundary
conditions are adopted in all three directions. The wavenumber of the
forcing is
.
Periodic boundary
conditions are adopted in all three directions. The wavenumber of the
forcing is
![]() .
As in BBS2001 the forcing amplitude is f0=0.01 and the nominal shear is
.
As in BBS2001 the forcing amplitude is f0=0.01 and the nominal shear is
![]() .
This means that the resulting shear velocity (in the absence of magnetic stresses)
is then also of order unity, i.e. close to the speed of sound, and the
turbulent rms velocity is about a hundred times smaller.
As in BD2001, the gravitational potential varies sinusoidally in z with an
amplitude g0=0.5, so the density contrast is
.
This means that the resulting shear velocity (in the absence of magnetic stresses)
is then also of order unity, i.e. close to the speed of sound, and the
turbulent rms velocity is about a hundred times smaller.
As in BD2001, the gravitational potential varies sinusoidally in z with an
amplitude g0=0.5, so the density contrast is
![]() .
The main parameter that is varied in the models considered below is the
magnetic diffusivity
.
The main parameter that is varied in the models considered below is the
magnetic diffusivity ![]() ,
which is in the range
,
which is in the range
![]() .
.
| Run |
|
|
|
|
||
| A | 0.01 |
|
0.0030 | 2.2 | 0.005 | 0.002 |
| B | 0.01 |
|
0.0030 | 0.7 | 0.018 | 0.002 |
| C | 0.01 | 10-4 | 0.0035 | 0.23 | 0.013 | 0.001 |
| C2 | 0.005 | 10-4 | 0.005 | 0.35 | >0.012 | >0.0004 |
Once the magnetic field becomes strong the shear motion becomes reduced
significantly due to magnetic forces. We define the total kinetic energy
(per unit surface) as
![]() ,
where
,
where ![]() and
and ![]() are
the boundaries between halo and disc plane. (This expression for
are
the boundaries between halo and disc plane. (This expression for
![]() includes the energy contained in
the shear, in contrast to
includes the energy contained in
the shear, in contrast to
![]() which does not.)
When the field is still weak we have
which does not.)
When the field is still weak we have
![]() ,
but once the field is strong
this value gets significantly reduced by magnetic stresses; see Table 3. One should
keep this in mind when comparing the magnetic energies for the
different runs.
In the following we use rms values of velocity and magnetic field for
normalization purposes; these quantities are defined in terms of
,
but once the field is strong
this value gets significantly reduced by magnetic stresses; see Table 3. One should
keep this in mind when comparing the magnetic energies for the
different runs.
In the following we use rms values of velocity and magnetic field for
normalization purposes; these quantities are defined in terms of
![]() and M via
and M via
![]() and
and
![]() ,
respectively.
,
respectively.
In Fig. 11 we plot the resulting correlation between
![]() (
(
![]() )
and
)
and ![]() for a particular snapshot
at the end of Run A. The anticipated effect is relatively
well pronounced - much more than in the global disc simulations.
As expected (see VC2001), its sign changes where the local shear,
for a particular snapshot
at the end of Run A. The anticipated effect is relatively
well pronounced - much more than in the global disc simulations.
As expected (see VC2001), its sign changes where the local shear,
![]() ,
is reversed.
This supports the validity of the basic result of VC2001 that
such a correlation exists owing to the presence of shear.
,
is reversed.
This supports the validity of the basic result of VC2001 that
such a correlation exists owing to the presence of shear.
It turns out that the Vishniac-Cho correlation is in fact the most
significant correlation coefficient that changes sign when shear changes sign. In Appendix C
we have calculated, for this flow, all 81 correlation coefficients of
![]() .
The Vishniac-Cho correlation is given by the
sum of
.
The Vishniac-Cho correlation is given by the
sum of
![]() and
and
![]() .
These two
terms are indeed the most important ones. We note that the correlators
.
These two
terms are indeed the most important ones. We note that the correlators
![]() (for
(for ![]() )
are also relatively large, but they do not
change sign when the sign of the shear changes.
)
are also relatively large, but they do not
change sign when the sign of the shear changes.
Next, we need to check whether this flow is capable of dynamo action and whether large scale fields can be generated. If so, then this effect should be associated with a significant vertical transport of magnetic helicity (VC2001). Whether or not such a flux really helps the dynamo needs of course to be seen.
In this model we find dynamo action provided the magnetic Reynolds
number is large enough. In Table 3 we give various parameters for
the models considered. In Run A where
![]() (the
value used in BBS2001) the dynamo growth rate,
(the
value used in BBS2001) the dynamo growth rate,
![]() ,
is about
,
is about
![]() .
This is much less than in the case with helical forcing where
.
This is much less than in the case with helical forcing where
![]() .
As in B2001 and BBS2001 the initial field strengths are about 10-6.
Thus, in the present case the saturation time is about
.
As in B2001 and BBS2001 the initial field strengths are about 10-6.
Thus, in the present case the saturation time is about
![]() ,
compared to about 103 in BBS2001.
For
,
compared to about 103 in BBS2001.
For
![]() (Run C) the growth rate is about five times larger (0.0053)
and the resulting saturation time correspondingly shorter. The field
is concentrated at small scales and shows some loop-like pattern
within the turbulent layer; see Fig. 12.
In Fig. 13 we plot the evolution of magnetic
energies of the mean and fluctuating field components
within the turbulent zone,
(Run C) the growth rate is about five times larger (0.0053)
and the resulting saturation time correspondingly shorter. The field
is concentrated at small scales and shows some loop-like pattern
within the turbulent layer; see Fig. 12.
In Fig. 13 we plot the evolution of magnetic
energies of the mean and fluctuating field components
within the turbulent zone, ![]() .
Here, mean fields are defined with respect to averaging in the toroidal
direction. Large scale magnetic fields are not present in the
bulk of the turbulent layer, but can be seen in the halo, especially
at later times.
.
Here, mean fields are defined with respect to averaging in the toroidal
direction. Large scale magnetic fields are not present in the
bulk of the turbulent layer, but can be seen in the halo, especially
at later times.
In Run A where
![]() there is significant magnetic
energy in the mean magnetic field (upper panel of Fig. 13),
but this mean field diminishes and the fluctuating field gains in
strength as the magnetic diffusivity is lowered to
there is significant magnetic
energy in the mean magnetic field (upper panel of Fig. 13),
but this mean field diminishes and the fluctuating field gains in
strength as the magnetic diffusivity is lowered to
![]() (Run C).
(Run C).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{h2980f13.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg209.gif) |
Figure 13:
Normalized magnetic energies in the mean and fluctuating components for Runs A
and C. Time is given in units of the inverse growth
rate (
|
Next we look at the evolution of magnetic and current helicities;
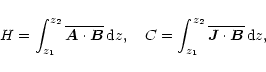 |
(10) |
As expected, because there is no net helicity in the forcing of the flow,
there are also no net magnetic and current helicities in the fields;
see Fig. 14. The fluctuations of magnetic helicity are generally
weak, but the contributions from the mean and fluctuating fields are
comparable. For the current helicity there is a clear dominance of the
small scale fields over the large scale fields. This is explained by
the fact that the current helicity has two k-factors more than the
magnetic helicity and hence the ratio of small scale to large scale
contributions are larger by a factor
![]() for current
helicity relative to magnetic helicity.
for current
helicity relative to magnetic helicity.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{h2980f14.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg214.gif) |
Figure 14:
Magnetic and current helicities in the mean and fluctuating components
for the run with
|
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{h2980f15.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg215.gif) |
Figure 15:
Magnetic helicity flux density in Coulomb gauge (upper panel)
compared with that in the |
Vishniac & Cho (2001) pointed out that the ![]() gauge in Eq. (8)
is not suited for analysing local helicity flux densities.
We recall that the procedures of Berger & Field (1984) and BD2001
only apply to helicities in a given volume and the corresponding
helicity fluxes through its bounding surface. Magnetic helicity
densities and the corresponding flux densities are only possible
to define in a given gauge.
gauge in Eq. (8)
is not suited for analysing local helicity flux densities.
We recall that the procedures of Berger & Field (1984) and BD2001
only apply to helicities in a given volume and the corresponding
helicity fluxes through its bounding surface. Magnetic helicity
densities and the corresponding flux densities are only possible
to define in a given gauge.
In the following we denote by
![]() the magnetic vector
potential in the Coulomb gauge, whilst
the magnetic vector
potential in the Coulomb gauge, whilst ![]() still refers to the
vector potential in the
still refers to the
vector potential in the ![]() gauge. The conversion between the
two is given by
gauge. The conversion between the
two is given by
![]() ,
where
,
where
![]() and
and
![]() .
In the following we use
the notation
.
In the following we use
the notation
![]() .
.
In the ![]() gauge the magnetic helicity flux density is simply
gauge the magnetic helicity flux density is simply
![]() ,
but when converted into the Coulomb gauge it becomes
(see Appendix D)
,
but when converted into the Coulomb gauge it becomes
(see Appendix D)
There may be additional solenoidal contributions also from
![]() .
In general
we may split
.
In general
we may split
![]() into an irrotational and a
solenoidal part,
into an irrotational and a
solenoidal part,
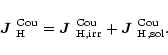 |
(12) |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{h2980f16.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg230.gif) |
Figure 16:
Time averaged vertical magnetic helicity flux density at x=0 as
a function of z in different gauges.
|
In order to assess the possibility of dynamo action we plot in
Fig. 17 vertical profiles of the divergence
of the helicity flux density, in units of
![]() .
This non-dimensional quantity is reminiscent of a local dynamo number,
.
This non-dimensional quantity is reminiscent of a local dynamo number,
![]() ,
where
,
where
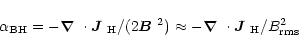 |
(13) |
Figure 17 shows that the non-dimensional measure
of the
![]() fluctuates around
fluctuates around ![]() .
This value should
be compared with the critical value of
.
This value should
be compared with the critical value of
![]() above which dynamo action is possible. We define the dynamo
number as
above which dynamo action is possible. We define the dynamo
number as
![]() ,
where
,
where
![]() .
With
.
With
![]() and
and
![]() we have
we have
![]() ,
and since the critical dynamo number is around 2 (BBS2001) we have 0.01, which agrees with the estimate above
(cf. Fig. 17). However, this estimate has been
too optimistic in several ways: the actual value of S is smaller than S0and the incoherent
,
and since the critical dynamo number is around 2 (BBS2001) we have 0.01, which agrees with the estimate above
(cf. Fig. 17). However, this estimate has been
too optimistic in several ways: the actual value of S is smaller than S0and the incoherent ![]() effect dynamo will be less efficient.
This may explain why the Vishniac-Cho effect does not seem to operate in
the present simulations, but it may become more
important at higher magnetic Reynolds numbers.
effect dynamo will be less efficient.
This may explain why the Vishniac-Cho effect does not seem to operate in
the present simulations, but it may become more
important at higher magnetic Reynolds numbers.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{h2980f17.ps}\end{figure}](/articles/aa/full/2001/46/aah2980/Timg244.gif) |
Figure 17:
Divergence of the mean helicity flux, normalized to make it similar
to a local dynamo number. As in Figs. 15 and 16, only
the contributions from the fluctuating components of |
Copyright ESO 2001