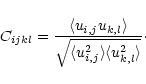 |
(C.1) |
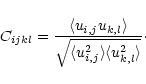 |
(C.1) |
![\begin{displaymath}C^{(S)}_{ijkl}={\textstyle{1\over2}}[C^{(+)}_{ijkl}+C^{(-)}_{...
...}_{ijkl}={\textstyle{1\over2}}[C^{(+)}_{ijkl}-C^{(-)}_{ijkl}],
\end{displaymath}](/articles/aa/full/2001/46/aah2980/img279.gif) |
(C.2) |
| l=1 | l=2 | l=3 | ||||||
| 1.00 | 0.04 | -0.09 | 0.04 | 1.00 | -0.14 | -0.09 | -0.14 | 1.00 |
| 0.02 | -0.01 | -0.01 | -0.26 | -0.03 | 0.03 | -0.03 | 0.01 | 0.03 |
| 0.01 | 0.05 | -0.23 | 0.10 | 0.10 | -0.02 | -0.54 | -0.01 | 0.04 |
| 0.02 | -0.26 | -0.03 | -0.01 | -0.03 | 0.01 | -0.01 | 0.03 | 0.03 |
| 1.00 | -0.00 | -0.03 | -0.00 | 1.00 | -0.01 | -0.03 | -0.01 | 1.00 |
| -0.03 | 0.02 | -0.04 | 0.00 | 0.07 | -0.07 | -0.03 | -0.60 | 0.06 |
| 0.01 | 0.10 | -0.54 | 0.05 | 0.10 | -0.01 | -0.23 | -0.02 | 0.04 |
| -0.03 | 0.00 | -0.03 | 0.02 | 0.07 | -0.60 | -0.04 | -0.07 | 0.06 |
| 1.00 | -0.00 | -0.03 | -0.00 | 1.00 | -0.13 | -0.03 | -0.13 | 1.00 |
| l=1 | l=2 | l=3 | ||||||
| 0.00 | -0.16 | -0.01 | -0.16 | 0.00 | -0.06 | -0.01 | -0.06 | 0.00 |
| -0.01 | 0.00 | 0.00 | 0.01 | -0.17 | 0.09 | 0.00 | 0.02 | -0.13 |
| -0.15 | -0.02 | 0.00 | -0.03 | -0.04 | 0.21 | 0.01 | 0.28 | -0.07 |
| -0.01 | 0.01 | 0.00 | 0.00 | -0.17 | 0.02 | 0.00 | 0.09 | -0.13 |
| 0.00 | -0.04 | 0.11 | -0.04 | 0.00 | -0.01 | 0.11 | -0.01 | 0.00 |
| 0.01 | 0.03 | 0.10 | 0.00 | 0.03 | -0.00 | 0.05 | -0.02 | 0.01 |
| -0.15 | -0.03 | 0.01 | -0.02 | -0.04 | 0.28 | 0.00 | 0.21 | -0.07 |
| 0.01 | 0.00 | 0.05 | 0.03 | 0.03 | -0.02 | 0.10 | -0.00 | 0.01 |
| 0.00 | -0.51 | 0.10 | -0.51 | 0.00 | 0.00 | 0.10 | 0.00 | 0.00 |
In Table C.1 the largest contributions come from C(S)xyyx=-0.26, C(S)yzzy=-0.60, and C(S)zxxz=-0.54. In Table C.2 the largest contributions come from C(A)xzzy=+0.28 and C(A)zxzy=-0.51. These are also the coefficients that are important in the Vishniac-Cho correlation.
Copyright ESO 2001